Immunization and Duration

Here, I use two cases to show how duration can be used to immunize a portfolio from changes in interest rates. The first case is simple: consider an employer with a single pensioner who is to retire in 10 years and to whom is promised $1 million at that time—in this case, a single balloon payment. (See Luenberger, Example 3.10). The employer wishes to invest an amount of money now to pay this obligation 10 years hence. This is, in fact, a simple example of liability-driven investment that is popular in corporate defined benefit pension plan management. If there were a 10-year zero coupon bond, the problem would be solved immediately because the zero would have duration matching the duration of the obligation—just calculate the amount of the zero necessary to produce $1 million in 10 years. Suppose, however, there are no zeros available. Instead, suppose the choice is among three coupon bonds: a 30-year, a 20-year, and a 10-year bond. As we shall see, the employer need consider purchasing only two bonds.

Go to the companion website for more details (see Duration for specifics on each bond).

Intuitively, the portfolio of bonds should be selected such that the present value of the portfolio is exactly equal to the present value of the $1 million obligation and, secondly, that the duration of the portfolio is as close as possible to the duration of the obligation. Thus, the portfolio must offset both the value and the timing of the obligation. There are two necessary conditions here that we can use to solve for the required proportions of each bond in the portfolio that will serve to discharge the obligation when the time comes. And, as we shall see as well, the value of the portfolio will move in tandem with the value of the obligation in the event that interest rates (that is, the discount rate) change over the 10-year period in question. Thus, this portfolio's value is immunized against unexpected changes in interest rates; as such, one need hold only the original shares of the bonds in this portfolio.

Denote the investments in the two bonds as P₁ and P₂ and their respective durations as D₁ and D₂. Then, formally, we require the two conditions:

1. , which says that the present value of the obligation must equal the portfolio value of the two coupon bonds. Moreover, we require

2. . This means that the duration-weighted sum of the bond prices must equal the duration-weighted present value of the obligation.

Assume all are par bonds and that the annual interest rate is 9 percent. Then the durations are 10.78, 9.61, and 6.8 years for the 30-year, 20-year, and 10-year bonds, respectively. Since the duration of the obligation is 10 years, then no single bond will suffice. However, a linear combination of bonds will work as long as this portfolio includes the 30-year bond; that is, there is some weighted average of the 30- and 20-year bonds or the 30- and 10-year bonds that have a duration of 10 years.

Since bonds pay semiannual coupons, then interest is compounded semiannually. We will use this formulation in computing the present values of all assets and liabilities. For example, the PV of the obligation is , since the yield is assumed to be 9 percent. D₁ and D₂ are known as well. Therefore, we have two equations in two unknowns, P₁ and P₂. Solving these will generate the total investment X Corporation needs to make in each bond.

Solution

Find the solution to this system of equations (Note: Because of the rounding of the duration estimates, the calculations may not be exact):

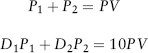
First, solve the first equation for P₁:

Second, substitute the solution for P₁ into the other equation and solve for P₂:

Third, substitute P₂ back into the first equation in order to get P₁ in terms of PV and durations:

Combination 1: 30-Year and 20-Year

Combination 2: 30-Year and 10-Year

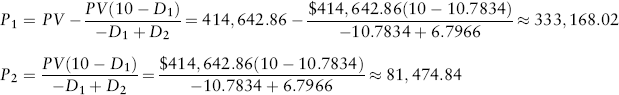
Dividing these values by the computed bond prices gives the numbers of units needed in each bond. Notice that by definition.

This is an example of a flat yield curve, or as we will understand in the next chapter, a flat term structure in which all maturities have the same yield. If the yield changes from 9 percent, then D₁, D₂, P₁, P₂, and P will change as well, but their changes will be offsetting so that the portfolio value matches that of the obligation. Therefore, the parameters of the model have changed. But the original number of bonds purchased for the portfolio remains the same. This means that the value of the portfolio has changed as shown in Table 2.6 As you can see, if yields fall to 8 percent, then bond prices P₁ and P₂ have risen, PV has risen, but is still essentially the same as PV. Note that immunization requires shorting the 30-year bond when yields fall to 8 percent. This is because the duration on the 20-year bond is now 10.06 which, by itself, almost exactly matches the duration on the liability. Thus, the second, longer-duration 30-year bond is not needed and is therefore sold short to provide funds to purchase more of the 20-year bond.

Table 2.6 Immunizing against Interest Rate Movements.

Immunization also holds in the opposite direction for small increases in rates to, say, 10 percent. Therefore, the value of the portfolio relative to the obligation is immunized from interest rate changes and the employer has constructed a dynamic hedge against interest rate risk, ensuring that the obligation can be met with no further investment.