Portfolio 5: Maximum Risk-Adjusted Return

We solved this portfolio previously but we did not examine its properties. We shall do that now. The objective is to find the portfolio that maximizes risk-adjusted return, that is,

The first term, w′r, is the portfolio return, while w′Vw is the variance of the returns on the portfolio w. This is particularly straightforward to solve by differentiation with respect to w′:

Solving this first order condition yields the portfolio:

Let's examine the intuition here. If we revert to the two-asset case that we have been studying, then we would write the objective function as follows:

This has two first order conditions:

Simplifying, and rewriting in matrix format, we get the following two-equation system:

The covariance matrix is diagonal in our preceding applications and making the following substitutions:

which give us the solution by inverting the covariance matrix and post-multiplying it by the returns vector, yielding the vector . Since we did not impose an adding-up constraint, let us do so now. Dividing each weight by the weight sum 0.4 clearly shows that this portfolio equally weights the two assets at 0.5 each. This is not coincidental. Look again at the covariance matrix. Since it's diagonal, its inverse is also a diagonal matrix with elements equal to the reciprocals of the variances, that is:

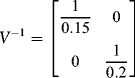
When we post-multiply by the returns vector, we get a 2 × 1 vector of the returns divided by their respective variances (see the appendix for a review of matrix operations):

We are looking at return per unit risk and that is exactly what this portfolio maximizes. The diagonal covariance matrix adds a lot of transparency to this intuition. In the case for which the returns to these two assets are not independent of each other, then the inverse of the covariance matrix is more complicated because risks to each asset are a combination of their individual risks (variances) plus the contribution to risk carried by their covariation with the other asset. But the intuition holds nonetheless. You should confirm that this portfolio will have return equal to 3.5 percent, with risk 29.58 percent and Sharpe ratio of 0.118 and that this Sharpe ratio is the highest of any portfolio. We are assuming that the risk-free rate is zero. Referring back to the capital market line, this portfolio is the tangency point on a line with intercept equal to the risk-free rate and slope equal to , where the subscript p denotes this portfolio's return and risk. Stated differently, no other mean-variance efficient portfolio can have a higher Sharpe ratio than the tangency portfolio.