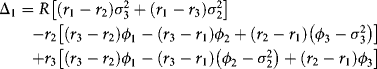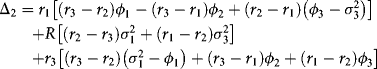Optimal Rebalancing in a Static Optimization Model

We desire to minimize the two-part loss quadratic as a function of portfolio drift subject to the standard adding-up constraint with portfolio return equal to the weighted sum of individual asset returns:

Here, V = variance-covariance matrix of returns, w is row vector of weights on a three-asset mix (stocks, bonds, cash), T indexes the target weight, and k is a column vector of transactions costs. Drift increases losses quadratically (the first term) but drift also avoids trading costs (second term). The net cost is convex in drift, which, in principle, possesses a minimum. The constraints require that weights sum to unity and that the target portfolio return is R.

Imposing the constraints, differentiating with respect to the weight vector and collecting terms generate (in the three-asset case) the following matrix of first-order conditions:

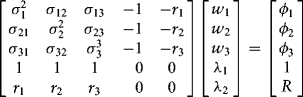
The square matrix has determinant:

In the case of zero covariances, this reduces to:

In general, Cramer's rule generates solutions:

Specifically,

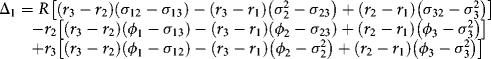
Solutions to and can be derived by similar means. Each of the computed weights is a rather complicated linear combination of variances, covariances, target weights, and relative returns. It can be shown that the comparative statics do not depend upon the covariances. Since this simplifies the comparative static computations, the remainder of the analysis assumes zero covariances, which generate, in addition to the zero-covariance value for Δ already given earlier: