The Gordon Growth Model
Let's return to the fundamental pricing model. The dividend discount model derived earlier is closely related to the Gordon Growth model. The latter also assumes that the market is infinitely lived and pays a periodic dividend (d), but which grows at a rate (g) over time. The current price of the index (p) is therefore the present value of the cash flow stream (we will derive our results without time subscripts):
Solving this power series yields the following for which price is essentially the capitalized value of the expected dividend payout in the next period:
If we assumed zero growth, then the Gordon Growth is identical to the dividend discount model derived at the beginning of this chapter. If dividends are expected to grow at a rate g, then for a given level, p, we can solve for the return on equity, r, as:
For example, assume that the growth rate of nominal earnings is 5 percent and the dividend payout is .40. Also assume that the current price level on the S&P is 900 and that the current p/e multiple is 13.3. Then the p/d multiple is p/(.4e) = 13.3/.4 = 33.25 and the Gordon Growth model forecasts a return, r = 1.05/33.25 + .05 = .0816. or 8 percent. If the yield on the 10-year Treasury is 4 percent, then the implied equity risk premium is 4 percent. Again, this is meant to be purely illustrative. For example, had we used an earnings growth of 7 percent, our forecasted return would be above 10 percent.
If we assume a constant dividend payout ratio, we can then convert the model to study the relationship between the p/e ratio and returns over time. Setting 
, where 
is the dividend payout ratio (0.4 in the preceding example):
It's easy to see that dividing both sides by earnings transforms the pricing model into a p/e model. We return to this relationship later.
(Equation (4.1)) is, in fact, a perpetuity (consol). We observe the price (p) and wish to solve for the return (the yield), which in this case is an internal rate of return (IRR). Let's fix a 10-year forecast horizon that implies the following (with n = 10):
Dividends (
) are assumed to grow at rate 
annually for n years, and the return r discounts these cash flows to equal the current price of the index. This is still a perpetuity because the terminal condition 
is the discounted present value of all cash flows realized after the nth year. It is written as:
We can still solve equation (4.3) as a closed form. Doing so, we get:
This says that the residual value of the asset after n years is the capitalized value (where the cap rate is 
) of the earnings at that time (which is given in the numerator). Plugging this into equation (4.2) will give us a closed form that we can solve in a spreadsheet.
This model discounts 10 years of expected cash flows but imposes a price correction factor that uses the condition that the terminal price 
be equal to the long-term average p/e multiple times earnings.
Thus, there are two parts to this model—the first part is the sum of the n cash flows that span the forecast horizon and the second part is the price correction embedded in the terminal value, which in this case is imposed to be consistent with a long-term p/e multiple. We can see therefore that this model is also mean reverting because it imposes the constraint that market price at the end of n years reverts back to the price implied by a long-term p/e multiple.
Using this model, we estimate a set of forward returns for a 10-year period over a range of starting prices and p/e ratios. These are presented in Table 4.1. The top row is the current price of the index. The remaining rows are forward returns conditional on each starting index value with price correction given by final p/e shown in the last column on the right. These calculations assume current annual earnings of $100 with dividend payout equal to 40 percent and nominal annual dividend growth of 4 percent. Historically, average nominal dividend growth has been 4 percent and the Shiller p/e using 10-year trailing average earnings is about 15. Dividend payout in 2009 was 43 percent. For example, if the current value of the index is $1,200, and the terminal p/e is set at 15, then the forward expected return is 8.8 percent.
Table 4.1 Forward Returns Conditional on Ending P/E and Current Price.
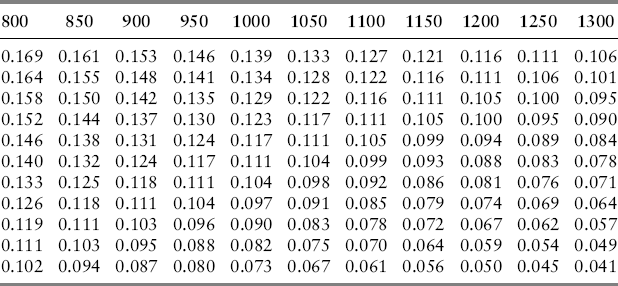
These estimates are quite sensitive to both starting price and ending value (p/e × earnings). It is tempting to apply a model like this to day-to-day movements in the index which, during turbulent times, can give off highly volatile point estimates as shown within the table. One should be cautioned: The purpose of the model is to forecast returns over the long run; price corrections may take a lot less time to revert. Nevertheless, the model will conclude that the impact on returns is averaged over a much longer time when in fact it may not be. The point is that we use a model like this to arrive at an estimate of the long-run mean return and not periodic point estimates, which are highly variable.
The forward return we solve for holds for the 10-year horizon. But, what does this return imply for the horizon beyond the tenth year? These results are provided in the shaded column. To see how these numbers are estimated, recall that the p/e ratio at year n is defined by equation (4.4) as:
The first term is the p/e at time n. This is set to some integer, say, m = 15, that imposes the terminal value of the index. The question of interest now is what the multiple m implies about the return that is required from year 10 onward that is consistent with the return solved for the first 10 years. For example, we just showed in the preceding example that the average forward return (the IRR, if you will) for the first 10 years is 8.8 percent. But, the forward return for years 11 onward is different. Plugging our numbers into the previous equation describing the terminal p/e, it must satisfy the following:
The return that satisfies this relation is 5.6 percent. Thus, we have implicitly constrained the return for the future beginning after the tenth year. Implicitly, this return, too, is part of our forecast indicating that there are two forward returns that equate discounted cash flows to current price—one for the first 10 years and one thereafter.
To see this implication more clearly, Table 4.2 presents the unconstrained forward return, that is, the very-long-term return with no price correction imposed; it is the solution to (equation (4.1)).
Table 4.2 Forward Returns with No Price Correction.
Since there is no terminal condition, meaning no price correction, then we get a single solution—not to 10 years but for all years. This indicates that the forward expected return on the index priced currently at $1,200 is 7.5 percent. There is no assumption about future index levels. Thus, Table 4.1 presents two separate forward returns; in this case, when the index value is currently $1,200 (which is about 12× earnings) and we require a future p/e ratio to rise to 15, then we require 8.8 percent growth in the first 10 years, followed by 5.6 percent growth thereafter. Alternatively, we could require 7.5 percent growth with no price correction imposed.
Here is a better example. Suppose the index falls to 800, which is consistent with a multiple of 8×. Table 4.1 shows, for all cases, the forward return on the index will have to be at least 10.2 percent if the multiple is to be anywhere above 10×. So, most of the forward-looking return is front loaded while the return after the tenth year is somewhat less at 9.2 percent. Experimenting with the length of the horizon shows that making n small forces the price correction into the first n years with the slack occurring thereafter. The point here is to recognize that results presented in Table 4.1 are sensitive to n but the results in Table 4.2 are not.