Principal Components
Think of a set R of T historical returns on k assets so that R ![]() T × k. There are, at best, k independent sources of variation in this set of returns. If, for example, one of the asset's returns can be expressed as a linear combination of another asset's returns, then there are only k – 1 independent sources of variation. In that case, the k × k covariance matrix would not be invertible since it has less than full rank; its rank is k – 1. Without full rank, we could not solve for the minimum variance portfolio. The reason is that we are asking too much of our data: it can provide us with only k – 1 weights, not k. At the other extreme, if the asset returns are independent, then there are k independent sources of variation (called factors) and the covariance matrix has full rank, whose diagonal elements contain variances of the individual asset returns and zeros otherwise.
T × k. There are, at best, k independent sources of variation in this set of returns. If, for example, one of the asset's returns can be expressed as a linear combination of another asset's returns, then there are only k – 1 independent sources of variation. In that case, the k × k covariance matrix would not be invertible since it has less than full rank; its rank is k – 1. Without full rank, we could not solve for the minimum variance portfolio. The reason is that we are asking too much of our data: it can provide us with only k – 1 weights, not k. At the other extreme, if the asset returns are independent, then there are k independent sources of variation (called factors) and the covariance matrix has full rank, whose diagonal elements contain variances of the individual asset returns and zeros otherwise.
The idea of the diagonal covariance matrix is intriguing for two reasons: first, it would suggest that returns are independent and that has important implications for diversification. Second, it simplifies the math; for example, solving the minimum variance portfolio is a matter of ranking the individual variances (or Sharpe ratios), giving highest weight to the lowest variance (highest Sharpe ratio).
Principal components analyzes the covariance properties of a set of returns or factors and finds the set of orthogonal factors that best explains the covariation of returns. Orthogonality means that the return vectors are at right angles—therefore, their inner products are zero. Thus, orthogonality implies independence. These orthogonal factors are the eigenvectors of the covariance matrix. There are k of them. Thus, for R ![]() T × k there are k eigenvectors, with each eigenvector corresponding to a single eigenvalue or characteristic root (we will derive these shortly). In the preceding case in which one asset's return depends upon another asset's return, then there would be a single eigenvalue equal to zero. As such, there would be k – 1 eigenvectors and only k – 1 factors to be recovered.
T × k there are k eigenvectors, with each eigenvector corresponding to a single eigenvalue or characteristic root (we will derive these shortly). In the preceding case in which one asset's return depends upon another asset's return, then there would be a single eigenvalue equal to zero. As such, there would be k – 1 eigenvectors and only k – 1 factors to be recovered.
Let's talk a bit about the intuition here before getting into the mathematics of eigenvalues. As demonstrated in previous sections of this chapter, factor models, in general, endeavor to describe the variation in returns, whether that is a cross-sectional variation or a time series variation. The factor model projects the asset's returns into the space spanned by the factors using a regression model, and the coefficients are used to weight the factors generating an expected, or conditional, return. Principal component analysis finds the set of independent factors that accounts for the cross- sectional variation in the set of returns R.
I will first introduce you to the principal components using a simple example to fix ideas and then expand the method using observed historical data. Suppose we have the following 2 × 2 matrix V (financial economists study covariance matrices, so keep that in mind as we move through this example).
![]()
We want to find the eigenvalues, associated eigenvectors, and principal components associated with this covariance matrix. The first step is to find the eigenvalues or roots λ by solving the determinant:
![]()
The determinant is –(1 + λ)(2 − λ) − 4 = (λ − 2)(λ − 3), which we set to zero and solve for λ. Thus, we want the solution to the quadratic equation: λ2 – λ – 6 = 0. The solution involves two roots, which are (λ1,λ2) = (−2,3). The second step substitutes each root in turn to solve for the two eigenvectors. This gives us, first, for λ = 3:
![]()
The eigenvector associated with this root is solved using the form:
![]()
Here ![]() is the eigenvector that projects the matrix into the null space. This can be solved by inspection to be
is the eigenvector that projects the matrix into the null space. This can be solved by inspection to be ![]() . To get a unique solution, we normalize by restricting the sum
. To get a unique solution, we normalize by restricting the sum ![]() . Substituting
. Substituting ![]() produces the restricted sum
produces the restricted sum ![]() , or
, or ![]() . Therefore,
. Therefore, ![]() . With that, we find the first eigenvectors associated with the eigenvalue λ = 3 to be:
. With that, we find the first eigenvectors associated with the eigenvalue λ = 3 to be:
![]()
Repeating this process for the second root, λ = −2, we solve the second eigenvector:
![]()
We now transform the original matrix V into a diagonal matrix consisting of two independent (orthogonal) vectors, using these two eigenvectors:
![]()
Let's label matrix ![]() . The columns of P are orthogonal and the trace of this matrix is the sum of the eigenvalues. Therefore, if we let X denote the matrix of eigenvectors, then we have XVX' = P. Note that the columns of X are orthogonal as well as those of P. Thus, these two eigenvectors form a basis in two-dimensional space R2.
. The columns of P are orthogonal and the trace of this matrix is the sum of the eigenvalues. Therefore, if we let X denote the matrix of eigenvectors, then we have XVX' = P. Note that the columns of X are orthogonal as well as those of P. Thus, these two eigenvectors form a basis in two-dimensional space R2.
I illustrate using monthly returns data from 1988 to 2009 given in the Chapter 9 examples spreadsheet on the princomp tab. Columns B to G contain monthly returns on benchmarks for six asset classes: U.S. equity, fixed income, non-U.S. equity, high yield, convertible bonds, and REITs. The covariance matrix is V ![]() 6 × 6:
6 × 6:

The covariance matrix of returns V has eigenvalues (roots):
| roots |
| 63.428 |
| 15.279 |
| 7.590 |
| 3.460 |
| 1.592 |
| 1.236 |
The roots are all strictly greater than zero, indicating a positive definite covariance matrix with full rank (it is therefore invertible). Dividing each root by the sum of the six roots gives the proportion of the total variation in the six returns that is accounted for by the eigenvector associated with that root. The first root, therefore, will account for 68.5 percent of the total cross-sectional variation in returns and succeeding roots less. Following our example, the eigenvectors are:
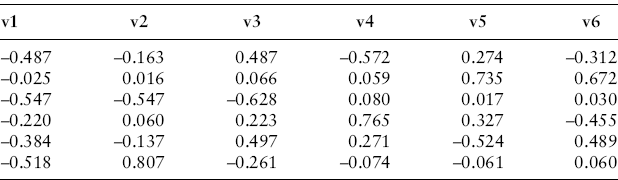
Letting R be the T × k = 264 × 6 returns matrix, then Rvi for i = 1,..., 6 is a T × 1 principal component vector. Each element in this principal component is a linear combination of the six returns for a given month times the elements in the eigenvector:
![]()
Repeating for each eigenvector generates a T × k matrix of principal components, which are given in rows I–N of the spreadsheet. One observation worth noting is that more often than not, it is difficult to discriminate among principal components because they are linear combinations of all the original factors. Thus, while we may have a set of orthogonal principal component factors, we may have difficulty interpreting them. The covariance matrix for the principal components will be a 6 × 6 diagonal matrix containing the eigenvalues along the diagonal.
Now, relating these results to the discussion at the beginning of this section, we find that the first principal component is a factor that accounts for 68.5 percent of the total variance in the cross-section of returns. Thus, these six asset returns share a common factor that accounts for the majority of their cross-sectional variation. If returns were truly independent, then V would be diagonal and the eigenvalues would account for shares of the cross-sectional variation, depending only on the returns’ relative variances.
Extending this thinking to a matrix of factors X ![]() T × k, we use principal components to generate a T × k matrix of orthogonal factors, with each factor a linear combination of the eigenvectors. In this case, we have the factor model r = Fβ + ε, where r is a T × 1 vector or returns, but where F is now a matrix of principal components derived from X. Decomposing the variance of returns yields:
T × k, we use principal components to generate a T × k matrix of orthogonal factors, with each factor a linear combination of the eigenvectors. In this case, we have the factor model r = Fβ + ε, where r is a T × 1 vector or returns, but where F is now a matrix of principal components derived from X. Decomposing the variance of returns yields:
![]()
Since cov(F) is diagonal, then the variance of the return can be decomposed into the scalar weighted sum of the variances of the orthogonal factors (the scalars being the estimated factor sensitivities in β) plus the idiosyncratic risk that is orthogonal to F. Therefore, for the nth firm,
![]()
Here, ![]() is the firm's idiosyncratic, or specific, risk. The systematic risk is composed of the sum of independent factor variances weighted by the squares of their factor sensitivities.
is the firm's idiosyncratic, or specific, risk. The systematic risk is composed of the sum of independent factor variances weighted by the squares of their factor sensitivities.
