4
Neural Learning and Control Co‐Design for Robot Arm Control
4.1 Introduction
The rapid advances of mechanics, electronics, computer engineering and control theory in recent years have significantly pushed forward the research on manipulators and gained great success in various industrial applications. Redundant manipulators are a special type of manipulators: they have more control degrees of freedom (DOFs) than task DOFs. Redundant manipulators have received intensive research focus for dexterous manipulation of complicated tasks.
A redundant manipulator provides a nonlinear mapping from its joint space to the Cartesian workspace. For the kinematic control of manipulators, it is desirable to find a control action in the joint space such that a reference motion in the workspace can be obtained. The solution to such a problem usually is not unique due to the redundancy and an optimal solution can be reached in terms of certain objective functions and a set of constraints. However, the nonlinearity of manipulators makes it difficult to directly solve the problem in the angle level with a satisfactory accuracy. Instead, most work considers this problem in the velocity space or acceleration space, where the mapping is converted to an affine function, and seek solutions in the new space. Benefiting from the affine nature of the manipulator kinematics in the velocity or acceleration space, early work [25] uses the pseudo‐inversion of a manipulator's Jacobian matrix to address the redundancy resolution problem. One by‐product of this solution is that it minimizes the kinematic energy consumption. However, this approach introduces intensive overhead for the computation of the pseudo‐inverse continuously with time [26]. To avoid the time‐consuming computation of the pseudo‐inverse, later work [3, 27] removes it by formulating this control problem as a quadratic programming, which minimizes kinematic energy consumption under some physical constraints. Generally, the analytical solution to this formulation cannot be obtained directly. Various matrix manipulations, e.g. matrix decomposition and Gaussian elimination, are employed to seek the numerical solutions [28]. However, the low efficiency of those serial processing techniques prohibits this type of method from real‐time control of manipulators.
As all parameters evolve continuously with time in the movement of manipulators, later work designs recurrent neural networks to inherit historically computed solutions. In this way, they can avoid the re‐computation of information from scratch and are able to gain improved performance in real‐time computing. In [32], the authors propose a Lagrange neural network model to minimize a cost function under an equation constraint. To deal with inequalities in constrained quadratic programming for manipulator redundancy resolution, researchers turn to consider the problem in its dual space and propose various dual neural network models for accurate solutions. In [34, 39], the authors analyze the problem in the dual space by introducing Lagrange dual variables and derive a convex projection function to represent inequality constraints. Due to the generality of dual neural networks in dealing with constrained quadratic programming problems, they are also extended to solve the redundancy resolution problem based on other alternative models of manipulators, e.g. acceleration space models [3]. To optimize the joint torque, a unified quadratic‐programming‐based dynamical system approach is established in [38] to control redundant manipulators. A dual neural network with simplified structure is proposed in [40] for the control of kinematically redundant manipulators.
Although great success has been gained for the kinematic control of redundant manipulators using dual neural network approaches, most existing solutions require an accurate knowledge of the manipulator model. This is in contrast to applications in the field of machine learning, where it is usually assumed that the model is unknown when using recurrent neural networks for different tasks. In this chapter, we fill this gap by providing a model‐free dual neural network for redundant manipulator control. Different from the pure learning problem of recurrent neural networks, the problem investigated in this chapter involves both learning and control, where they interact with each other.
4.2 Problem Formulation
The forward kinematics of a manipulator is concerned with a nonlinear transformation from a joint space to a Cartesian workspace as described by
where ![]() is an
is an ![]() ‐dimensional vector in the workspace describing the position and orientation of the end‐effector at time
‐dimensional vector in the workspace describing the position and orientation of the end‐effector at time ![]() ;
; ![]() is an
is an ![]() ‐dimensional vector in the joint space with each entry describing a joint angle; and
‐dimensional vector in the joint space with each entry describing a joint angle; and ![]() is a nonlinear mapping determined by the structure and the parameters of a manipulator. Due to the nonlinearity and redundancy of the mapping
is a nonlinear mapping determined by the structure and the parameters of a manipulator. Due to the nonlinearity and redundancy of the mapping ![]() , it is usually difficult to obtain the corresponding
, it is usually difficult to obtain the corresponding ![]() directly for a desired
directly for a desired ![]() . In contrast, the mapping from the joint space to the workspace in velocity level is an affine one and thus can significantly simplify the problem. To see this, computing the time derivative on both sides of (4.1) yields
. In contrast, the mapping from the joint space to the workspace in velocity level is an affine one and thus can significantly simplify the problem. To see this, computing the time derivative on both sides of (4.1) yields
where ![]() is the Jacobian matrix of
is the Jacobian matrix of ![]() ; and
; and ![]() and
and ![]() are the Cartesian velocity and the joint velocity, respectively. Each element of
are the Cartesian velocity and the joint velocity, respectively. Each element of ![]() , the angular speed of that particular joint, serves as an input and can be controlled by a motor. Define an
, the angular speed of that particular joint, serves as an input and can be controlled by a motor. Define an ![]() ‐dimensional input vector
‐dimensional input vector ![]() . Then, the manipulator kinematics can be rewritten as:
. Then, the manipulator kinematics can be rewritten as:
Due to physical limitations of motors, the angular speed of joints is limited to a bounded range. For example, the constraint ![]() applies to the case that each individual joint is restricted to a speed at maximum of
applies to the case that each individual joint is restricted to a speed at maximum of ![]() . To capture restrictions on
. To capture restrictions on ![]() , we set the following constraint for a general situation:
, we set the following constraint for a general situation:
where ![]() is a set in an
is a set in an ![]() ‐dimensional space. For a redundant manipulator described by (4.3) subject to the control input constraint (4.4), we aim to find a control law
‐dimensional space. For a redundant manipulator described by (4.3) subject to the control input constraint (4.4), we aim to find a control law ![]() such that the velocity tracking error
such that the velocity tracking error ![]() for a given reference signal
for a given reference signal ![]() converges with time.
converges with time.
4.3 Nominal Neural Controller Design
The kinematic control of redundant manipulators using a dual neural network has been extensively studied in recent years. Although existing methods in this class differ in choosing different objective functions or using different neural dynamics, most of them follow similar design procedures. This class of methods usually formulate the problem as a constrained quadratic optimization, which can be equivalently converted to a set of implicit equations. Then, a convergent dual neural network model with its equilibrium identical to the solution of this implicit equation set is thus devised to solve the problem recursively. Without losing generality, the corresponding optimization problem with the joint space kinematic energy ![]() as an objective function and with a constraint set to the joint velocity
as an objective function and with a constraint set to the joint velocity ![]() , where superscript
, where superscript ![]() denotes the transpose of a vector
denotes the transpose of a vector ![]() (or matrix), can be presented as follows:
(or matrix), can be presented as follows:
where ![]() is a convex set and
is a convex set and ![]() is a positive definite symmetric matrix. In most of the literature [38–40, 45, 46], the set
is a positive definite symmetric matrix. In most of the literature [38–40, 45, 46], the set ![]() is chosen as
is chosen as ![]() to capture the physical constraint on the limit of joint speeds. Choosing a Lagrange function as
to capture the physical constraint on the limit of joint speeds. Choosing a Lagrange function as ![]() , where
, where ![]() is the Lagrange multiplier corresponding to the equality constraint (4.5b), the optimal solution to (4.5) is equivalent to the solution of the following equation set according to the so‐called Karush–Kuhn–Tucker condition [11]:
is the Lagrange multiplier corresponding to the equality constraint (4.5b), the optimal solution to (4.5) is equivalent to the solution of the following equation set according to the so‐called Karush–Kuhn–Tucker condition [11]:
where ![]() is a constant,
is a constant, ![]() is a projection operation to a set
is a projection operation to a set ![]() which results in a value
which results in a value ![]() such that its distance to
such that its distance to ![]() is minimized in the sense of the Euclidean norm, i.e.
is minimized in the sense of the Euclidean norm, i.e. ![]() . A projected recurrent neural network to solve (4.6) can be designed as follows:
. A projected recurrent neural network to solve (4.6) can be designed as follows:
where ![]() is a scaling factor. The dynamics of (4.7) has been rigorously proved to converge to its equilibria that is identical to the optimal solution of (4.5) [39, 40].
is a scaling factor. The dynamics of (4.7) has been rigorously proved to converge to its equilibria that is identical to the optimal solution of (4.5) [39, 40].
4.4 A Novel Dual Neural Network Model
In this section, we present a novel dual neural network model to address the model‐free redundancy resolution problem of manipulators.
4.4.1 Neural Network Design
In this section, we design extra neural dynamics to learn the model of the manipulator, and use the online learned results to achieve the model‐free control of manipulators.
For the estimation purpose, we first construct a virtual reference ![]() with the following dynamic evolution to estimate
with the following dynamic evolution to estimate ![]() in the workspace:
in the workspace:
where ![]() is the estimation of the manipulator Jacobian matrix, and
is the estimation of the manipulator Jacobian matrix, and ![]() is the measured Cartesian velocity of the end‐effector in the workspace. As to
is the measured Cartesian velocity of the end‐effector in the workspace. As to ![]() , we devise the following dynamics for its estimation:
, we devise the following dynamics for its estimation:
where ![]() is a scaling factor. By replacing
is a scaling factor. By replacing ![]() in (4.7) with
in (4.7) with ![]() obtained in (4.9), the whole system obtained so far can be expressed as follows:
obtained in (4.9), the whole system obtained so far can be expressed as follows:
Consider a special case when the initial value of ![]() and
and ![]() at time
at time ![]() are both set at 0. In this situation, the immediate derivative of state variables can be obtained as
are both set at 0. In this situation, the immediate derivative of state variables can be obtained as ![]() ,
, ![]() ,
, ![]() , and
, and ![]() according to (4.10) and (4.3), implying that
according to (4.10) and (4.3), implying that ![]() ,
, ![]() , and
, and ![]() subsequently for
subsequently for ![]() . This reveals the failure of (4.10) for redundancy resolution. The reason lies in the fact that input–output pairs of the manipulator system, i.e. the
. This reveals the failure of (4.10) for redundancy resolution. The reason lies in the fact that input–output pairs of the manipulator system, i.e. the ![]() –
–![]() pairs, lack richness in such a scenario. In other words, there is not enough training data. Intuitively, as the proposed scheme involves both learning and control in a unified framework, it is more challenging than pure learning or identification of manipulator models. However, it also fails even for pure learning of manipulator models when there is only one pair of input–output data available. In this case, only the data pair, namely,
pairs, lack richness in such a scenario. In other words, there is not enough training data. Intuitively, as the proposed scheme involves both learning and control in a unified framework, it is more challenging than pure learning or identification of manipulator models. However, it also fails even for pure learning of manipulator models when there is only one pair of input–output data available. In this case, only the data pair, namely, ![]() and
and ![]() , is available. To avoid this dilemma, we intentionally add extra noises in
, is available. To avoid this dilemma, we intentionally add extra noises in ![]() to excite the system for the generation of diverging outputs. Specifically, we replace
to excite the system for the generation of diverging outputs. Specifically, we replace ![]() in (4.10) with
in (4.10) with ![]() for the consistency of notation, define a noise polluted version of
for the consistency of notation, define a noise polluted version of ![]() as
as ![]() , and propose the following neural adaptive law:
, and propose the following neural adaptive law:
where ![]() is a bounded zero mean
is a bounded zero mean ![]() deviation i.i.d. random noise with the bound
deviation i.i.d. random noise with the bound ![]() . About the extra noise
. About the extra noise ![]() , we have the following remark.
, we have the following remark.
The proposed neural law (4.11) provides a dynamic feedback for the control of a manipulator. In this dynamic feedback mechanism, ![]() ,
, ![]() , and
, and ![]() construct the state variables.
construct the state variables. ![]() is the output of this neural controller and also serves as the input of the manipulator dynamics (4.3). The expression of the neural law (4.11) does not include any manipulator parameter, which implies that the neural model presented in this chapter is a fully model‐free controller. The control is reached based on real‐time learning of manipulator characteristics driven by input–output data, i.e.
is the output of this neural controller and also serves as the input of the manipulator dynamics (4.3). The expression of the neural law (4.11) does not include any manipulator parameter, which implies that the neural model presented in this chapter is a fully model‐free controller. The control is reached based on real‐time learning of manipulator characteristics driven by input–output data, i.e. ![]() and
and ![]() .
.
Figure 4.1 shows the internal information flow of the proposed scheme. It can be observed that this neural network accepts three input variables, namely the reference speed signal ![]() , the real speed signal
, the real speed signal ![]() , and the additive noise
, and the additive noise ![]() , and outputs
, and outputs ![]() as the control action, which will be further used as the control input of the manipulator. Inside this neural network, the evolution of each of the state variables among
as the control action, which will be further used as the control input of the manipulator. Inside this neural network, the evolution of each of the state variables among ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , depends not only on itself but also on others, which work together to construct the recurrence of the model. Figure 4.2 shows the interconnection of the proposed neural network with a manipulator in a feedback loop for control. Note that the output of the neural network becomes the input of the manipulator and the real‐time measurements of the manipulator are then fed back to the neural network as its input, thereby forming a closed loop control.
, depends not only on itself but also on others, which work together to construct the recurrence of the model. Figure 4.2 shows the interconnection of the proposed neural network with a manipulator in a feedback loop for control. Note that the output of the neural network becomes the input of the manipulator and the real‐time measurements of the manipulator are then fed back to the neural network as its input, thereby forming a closed loop control.

Figure 4.1 The neural connections between different neural states in the proposed neural controller.

Figure 4.2 The control block diagram of the overall system using the proposed neural network for the control of a manipulator.
With respect to the difference of the proposed model from existing neural controllers for manipulator control, we have the following remark.
4.4.2 Stability
In this section, we present the stability theorem of the proposed solution (4.11) and its theoretical proof.
About this theorem, we have the following remark.
In addition, on the parameter selection in the proposed neural network, we have the following remark.
4.5 Simulations
In this section, we consider numerical simulations on a PUMA 560 manipulator to show the effectiveness of the proposed algorithms.
Table 4.1 Summary of the Denavit–Hartenberg parameters of the PUMA 560 manipulator used in the simulation.
| Link | |||
| 1 | 0 | 0.67 | |
| 2 | 0.4318 | 0 | 0 |
| 3 | 0.4318 | − |
0.15005 |
| 4 | 0 | 0 | |
| 5 | 0 | − |
0 |
| 6 | 0 | 0 | 0.2 |
4.5.1 Simulation Setup
The PUMA 560 (Figure 4.3) is an articulated manipulator with six independently controlled joints. The parameters of the PUMA 560 manipulator are summarized in Table 4.1. The end‐effector of a PUMA 560 manipulator can reach any position at any orientation in its workspace. In this simulation, we particularly consider the position control of the end‐effector in three dimensions. In this sense, the 6‐DOF PUMA 560 manipulator is a redundant manipulator relative to this particular task in a three‐dimensional space.

Figure 4.3 A schematic of the PUMA 560 manipulator.
In this simulation, the reference end‐effector movement is set as a circle. This circle is centered at ![]() with a radius 0.2 m and is inclined around the
with a radius 0.2 m and is inclined around the ![]() ‐axis for
‐axis for ![]() . The desired angular motion speed is set as 0.2 rad/s. The control scaling factor
. The desired angular motion speed is set as 0.2 rad/s. The control scaling factor ![]() in the neural model is set as
in the neural model is set as ![]() and the learning scaling factor
and the learning scaling factor ![]() is set as
is set as ![]() . The excitation signal
. The excitation signal ![]() is set as a random noise with zero mean,
is set as a random noise with zero mean, ![]() deviation and the bound
deviation and the bound ![]() . The goal to set the noise at a small value is to ensure a minimal impact on the system's performance. The projection set
. The goal to set the noise at a small value is to ensure a minimal impact on the system's performance. The projection set ![]() is set as
is set as ![]() .
.
4.5.2 Simulation Results
4.5.2.1 Tracking Performance
In this section, we show typical simulations on using the proposed neural network for the tracking of the circular motion. Note that the simulation is conducted under the condition that no prior knowledge about the manipulator parameters is employed. As shown in Figure 4.4, the end‐effector of the PUMA 560 manipulator is able to track the desired trajectory successfully based on the proposed neural model with the excitation signal ![]() . The time evolutions of the state variable
. The time evolutions of the state variable ![]() , the joint angle of the manipulator, and the estimated Jacobian matrix (a total of 18 elements) are shown in Figures 4.5a, 4.5b, and 4.6a, respectively. As observed, the signals evolve smoothly with time. Figure 4.6b shows the time evolution of
, the joint angle of the manipulator, and the estimated Jacobian matrix (a total of 18 elements) are shown in Figures 4.5a, 4.5b, and 4.6a, respectively. As observed, the signals evolve smoothly with time. Figure 4.6b shows the time evolution of ![]() , which captures the learning error. As demonstrated in this figure, the learning error converges to zero very fast and remains a small value at the level of
, which captures the learning error. As demonstrated in this figure, the learning error converges to zero very fast and remains a small value at the level of ![]() m/rad after convergence. Recall that the control objective for redundancy resolution is to find a proper value of
m/rad after convergence. Recall that the control objective for redundancy resolution is to find a proper value of ![]() such that the resulting end‐effector velocity matches the desired reference. With the computed control input, the velocity tracking error also converges to a very small value at the level of
such that the resulting end‐effector velocity matches the desired reference. With the computed control input, the velocity tracking error also converges to a very small value at the level of ![]() m/s after a short period of transition, as shown in Figure 4.7a. Overall, with the proposed control scheme, both the learning error
m/s after a short period of transition, as shown in Figure 4.7a. Overall, with the proposed control scheme, both the learning error ![]() in Figure 4.6b and the position tracking error
in Figure 4.6b and the position tracking error ![]() in Figure 4.7b converge to zero, which verifies the effectiveness of the proposed algorithm for simultaneous learning and control. The evolutions of the co‐state
in Figure 4.7b converge to zero, which verifies the effectiveness of the proposed algorithm for simultaneous learning and control. The evolutions of the co‐state ![]() and the control action
and the control action ![]() are shown in Figure 4.8a and b, respectively. Note that
are shown in Figure 4.8a and b, respectively. Note that ![]() differs from
differs from ![]() by the additive noises and the curve of
by the additive noises and the curve of ![]() in Figure 4.5a almost coincides with that of
in Figure 4.5a almost coincides with that of ![]() since the additive noise
since the additive noise ![]() is so small that
is so small that ![]() .
.

Figure 4.4 The trajectory of the manipulator end‐effector using the proposed algorithm with excitation noises, where the piecewise straight lines represent the links of the manipulator and the curve represents the trajectory of the end‐effector. (a)  –
– view; (b)
view; (b)  –
– view; and (c)
view; and (c)  –
– view.
view.

Figure 4.5 Simulation results using the proposed algorithm. Time history of (a)  and (
and ( )
)  .
.

Figure 4.6 Simulation results using the proposed algorithm. Time history of (a) all elements of the estimated Jacobian matrix  and (b) the Jacobian estimation error
and (b) the Jacobian estimation error  .
.

Figure 4.7 Simulation results using the proposed algorithm. Time history of (a) the position error  and (b) the resolved velocity error
and (b) the resolved velocity error  .
.

Figure 4.8 Simulation results using the proposed algorithm. Time history of (a) the co‐state  and (b)
and (b)  .
.
4.5.2.2 With vs. Without Excitation Noises
One key component of the proposed algorithm is the additive noise intentionally injected to the control loop to excite the system for effective learning. As proved in our theoretical results and numerically shown in the last section, manipulators with the proposed algorithm applied with excitation noises can successfully reach simultaneous learning and control. In this section, we show in a numerical experiment that the additive noise is necessary to avoid failure of the control task and the performance will degrade greatly after removing the additive noise. To verify this, we re‐run the numerical simulation under exactly the same setup as before but removing the additive noise. As shown in Figure 4.9, for the circular motion tracking task, the generated trajectory by the end‐effector when using the proposed algorithm without additive noise, is far from the desired circular motion, although it becomes smooth due to the absence of noises. In this situation, the Jacobian estimation error ![]() , which is at the level of 1.0 m/rad, the position error
, which is at the level of 1.0 m/rad, the position error ![]() , which is at the level of 0.1 m, and the velocity resolution error
, which is at the level of 0.1 m, and the velocity resolution error ![]() , which is at the level of 0.1 m/s, are all much greater than those of the proposed algorithm shown in Figures 4.5–4.8. This demonstrates the advantage of the proposed algorithm and verifies the importance of additive noise in such a control paradigm. On this point, we have the following remark.
, which is at the level of 0.1 m/s, are all much greater than those of the proposed algorithm shown in Figures 4.5–4.8. This demonstrates the advantage of the proposed algorithm and verifies the importance of additive noise in such a control paradigm. On this point, we have the following remark.

Figure 4.9 The trajectory of the manipulator end‐effector using the algorithm without additive noises, where the piecewise straight lines represent the links of the manipulator and the curve represents the trajectory of the end‐effector. (a)  –
– view; (b)
view; (b)  –
– view; and (c)
view; and (c)  –
– view.
view.
In addition, we conducted further simulations to test the performance of the system under different levels of measurement noises for ![]() . We consider additive white noise with zero mean and
. We consider additive white noise with zero mean and ![]() variance. As shown in Figures 4.11 and 4.12, with the increase of the measurement noise, the position tracking error increases but is always bounded.
variance. As shown in Figures 4.11 and 4.12, with the increase of the measurement noise, the position tracking error increases but is always bounded.

Figure 4.10 The trajectory of the manipulator end‐effector using the algorithm without additive noises. Time history of (a) the estimation error for the Jacobian matrix; (b) the position tracking error; and (c) the velocity tracking error.

Figure 4.11 The position tracking trajectory of the manipulator end‐effector under different levels of measurement noises of  . (a)
. (a)  and (b)
and (b)  .
.
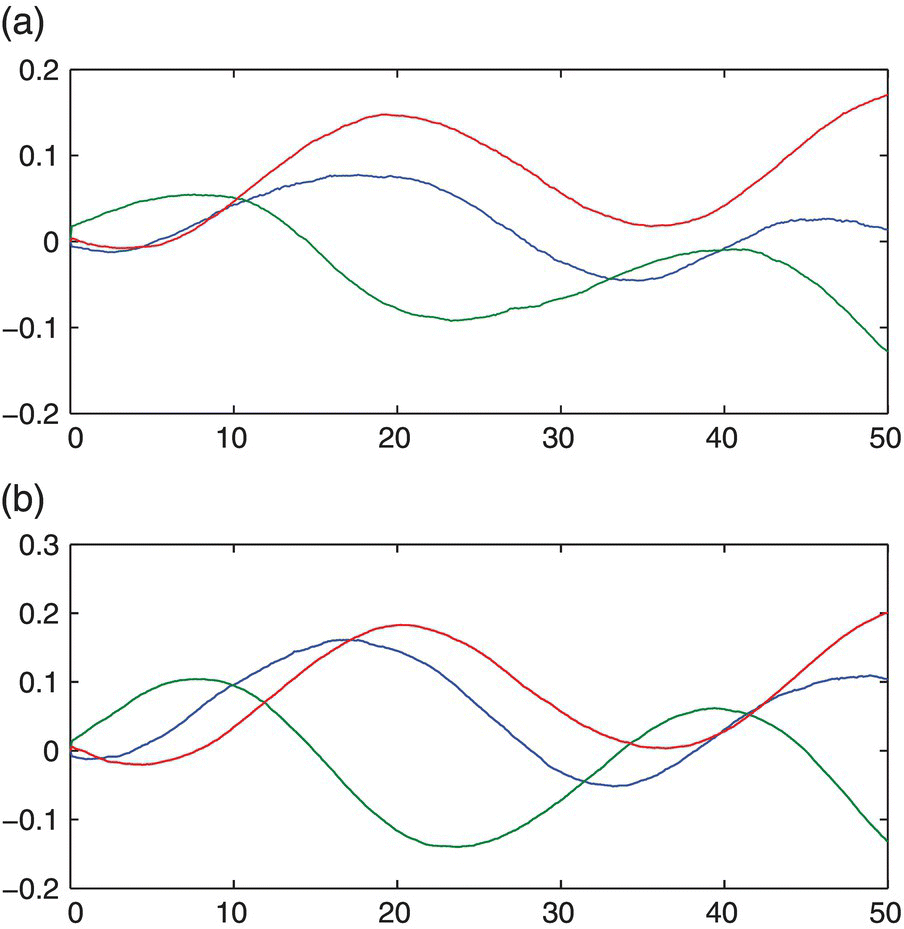
Figure 4.12 The position tracking trajectory of the manipulator end‐effector under different levels of measurement noises of  . (a)
. (a)  and (b)
and (b)  .
.
4.6 Summary
In this chapter, a model‐free dual neural network is presented to address the redundancy resolution problem of manipulators. The presented method does not require any knowledge of the manipulator parameters and is able to address the learning and control of manipulators in a unified framework. The presented neural network consists of neurons with dynamic dependence on their evolutions of state variables. In this novel design, an excitation signal is injected into the control channel for efficient model learning. The deliberate design guarantees that the estimation error converges to zero despite the additive excitation noise. Theoretical proofs are supplied to verify the stability of the presented models. Simulation results validate the effectiveness of the presented solution. To the best of our knowledge, this is the first work to address dual neural network models for model‐free simultaneous learning and control of redundant manipulators.


