6
Using Neural Networks to Avoid Robot Singularity
6.1 Introduction
In recent decades, robotics has attracted considerable attention in scientific research and engineering applications. Much effort has been spent to robotics, and different types of robots have been developed and investigated [61–68]. Among these robots, redundant robot manipulators, possessing more degrees of freedom (DOFs) in joint space than workspace and offering increased control flexibility for complicated tasks, have played a more and more important role in numerous fields of engineering applications [64], 68, 69. For example, the problem of finite‐time stabilization and control of redundant manipulators is investigated in [69], and a controller is designed to attenuate the effects of model nonlinearity, uncertainties, and external disturbances and improve the response characteristics of the system. The forward kinematics of a redundant manipulator provides a nonlinear mapping from its joint space to its operating region in Cartesian space. This nonlinear mapping makes it difficult to directly solve the redundancy resolution problem at the angle level. Instead, in most approaches, the problem is first converted into a problem at the velocity or acceleration level, and solutions are then sought in the converted space. A popular method is to apply the pseudoinverse formulation for obtaining a general solution at the joint‐velocity level. However, this strategy suffers from an intensive computational burden because of the need to perform the pseudoinversion of matrices continuously over time, in addition to the weakness that the joint physical limits are usually not considered [70, 71]. Recent progress shows the advantages of unifying the treatment of various constraints of manipulators' redundancy resolution into a quadratic program. Such a quadratic program formulation is general in the sense that it incorporates equality, inequality and bound constraints, simultaneously. For example, reformulated as a quadratic program, the equivalence between different‐level redundancy‐resolution of redundant manipulators is investigated in 72. Then, the work is extended in [68] for obstacle avoidance of redundant robot manipulators with the aid of a quadratic program. In addition to the control of redundant manipulators, the quadratic program is also exploited for the other types of robots, e.g. formation control of leader–follower mobile robots' systems in [61, 65, 73].
Neural networks, which feature capabilities of high‐speed parallel distributed processing, and can be readily implemented by hardware, have been recognized as a powerful tool for real‐time processing and successfully applied widely in various control systems [64–66, 72, 74–81]. Particularly, using neural networks for the control of robot manipulators has attracted much attention and various related schemes and methods have been proposed and investigated [64–66, 79, 80]. Cai and Zhang present two neural networks for the online solution of a quadratic programming problem existing in the redundancy resolution of manipulators in [72]. They further modify their work in [64] by proposing new noise‐tolerant neural networks with application to the motion generation of redundant manipulators. It is worth pointing out here that those neural networks presented in [64, 72] do not consider the bound constraint and thus cannot avoid the joint physical constraints in the manipulator applications. For the direct consideration of inequalities in constrained quadratic programming problems, researchers have attempted to consider the problem in its dual space. Various dual neural networks with different architectures have been proposed [68, 82–85]. The dual neural network based methods are highly efficient for real‐time processing and have been successfully used in various applications, including redundant manipulator control.
The performance index plays an important role in quadratic programming formulation based manipulator control, which, to some extent, determines the application potential of redundant manipulators in different industry fields. Therefore, how to model an efficient performance index is an important issue for the redundancy resolution. It is worth pointing out that when a manipulator is at a kinematic singularity configuration, its Jacobian matrix becomes ill‐conditioned and rank‐deficient [83]. In addition, getting close to a singularity point of the kinematic mapping is also undesirable and unacceptable due to the fact that, in such a state, when the end‐effector moves in certain directions, joint velocities and accelerations can be arbitrarily large and this may damage the manipulator. Therefore, research on maximizing the manipulability of manipulators has explicit significance and has been investigated widely. Yoshikawa establishes the first quantitative measure of the manipulability for redundant manipulators at the joint‐velocity level in [86]. The seminal study presented by Yoshikawa exploits the pseudoinverse‐type formulation to avoid the singularity of redundant manipulators by maximizing the manipulability measure. A multiobjective optimization of a hybrid robotic machine tool is presented in [87], which involves different types of manipulability. Note that most of the aforementioned techniques are based on pseudoinverse‐type formulations and do not consider physical limits of manipulators. Zhang et al. present a quadratic programming formulation based manipulability‐maximizing scheme, which can handle the physical limits. However, this scheme suffers from an intensive computational burden because of the need to perform the matrix inversion continuously over time in performance index [83]. Moreover, the tradeoff between manipulability and energy consumption is fixed in this scheme, which leads to less adaptation to environments. This chapter makes progress on this front through the modeling of the manipulability optimization of redundant manipulators and the proposal of dynamic neural network to remedy the weaknesses of existing schemes. Note that the scheme presented in [83], together with the other schemes mentioned, will be compared in detail in Section 6.6 to clarify the differences and advantages of the new scheme proposed.
6.2 Preliminaries
In this section, we present useful definitions and convergence lemmas that play an important role in the theoretical derivation in this chapter.
Projection operator. The projection operator for a set 
and 
is defined by
where 
denotes the Euclidean norm.
Normal cone. For a convex set 
and 
, the normal cone of 
at 
, denoted by 
, is defined as
Monotone mapping. A mapping 
is called monotone if for each pair of points 
, 
, there is
The above definition generalizes the definition of monotonicity from univariable mappings to multivariable mappings. Note that it is possible to verify the monotonicity of a univariable mapping by checking whether its derivative is greater than zero. Similarly, this property can also be extended to the general multivariable mapping 
. For a continuously differentiable mapping 
, it is a monotone mapping if
where 
means the left‐hand side of this operator is a positive semidefinite matrix.
For the projection operator and the normal cone, their relationship is summarized in the following lemma.
For a general dynamic systems, the so‐called LaSalle's invariance principle applies, as stated below.
For a time‐varying function, Barbalat's lemma holds.
For a class of well studied dual neural networks, one sufficient condition for its convergence has been established as in the following.
6.3 Problem Formulation
In this section, definitions on manipulator kinematics and manipulability are presented for problem formulation.
6.3.1 Manipulator Kinematics
For a 
‐DOF redundant manipulator with the joint angle 
, its Cartesian coordinate 
in the workspace can be described as a nonlinear mapping:
where the mapping 
carries mechanical and geometrical information of a manipulator. By definition, the joint space dimension 
of a redundant manipulator is greater than the workspace dimension 
, i.e. 
. Computing time derivations on both sides of (6.7), we have
where 
is called the Jacobian matrix of 
, and usually is abbreviated as 
. The end‐effector 
of the redundant manipulator is expected to track the desired path 
, i.e. 
with 
. It is worth pointing out here that, in the rest of this chapter, the argument 
is frequently omitted for presentation convenience, e.g. by writing 
as 
.
6.3.2 Manipulability
The manipulability of a robot manipulator is a function of the Jacobian matrix as defined below [88]:
where 
for 
is the ith largest eigenvalue of 
(note 
and thus its eigenvalues are all non‐negative). This measure gives an overall scalar description on the gain from joint velocity 
to 
and measures the amount of singularity. When the robot arm is singular, i.e. 
, 
reaches its least value 0. To increase the manipulability and avoid singularity, a large value of 
is preferable in operation.
6.3.3 Optimization Problem Formulation
Therefore, based on the above analysis, the redundancy resolution of a redundant manipulator with manipulability optimality considered is formulated as
So far the redundancy resolution has been formulated as a constrained optimization with the manipulator kinematics as an equation constraint and the manipulability as a cost to maximize. In this optimization problem, 
, as a function of 
, usually is nonconvex relative to 
. Additionally, the equation constraint is also usually nonlinear. Thus, the solution of 
in (6.10) becomes a challenging problem.
6.4 Reformulation as a Constrained Quadratic Program
Here, by incorporating physical constraints and redefining the objective function, we reformulate such a redundancy resolution problem with optimal manipulability considered into a constrained quadratic programming problem.
6.4.1 Equation Constraint: Speed Level Resolution
Equation (6.7) describes the mapping from the joint space to the workspace in position level and has a strong nonlinearity. As shown in (6.8), the mapping in velocity level can be significantly simplified. Defining 
as the end‐effector velocity in the workspace and 
as the joint angular velocity in the joint space and abbreviating 
as 
, Equation (6.8) can be rewritten as
This equation describes the kinematic mapping from the joint space to the workspace at velocity level. In comparison with the position level mapping (6.7) expressed as a general nonlinear function, the velocity level mapping is much simpler as it is in an affine form. Simply enforcing 
usually is able to obtain 
satisfying the speed requirement 
, but may suffer from drifting in position due to the loss of explicit information on 
. Instead, we restrict the motion of the redundant manipulator in the following way to reach a desired position.
where 
is the position error feedback coefficient. Note that 
. Accordingly, the above equation can be written as 
and is able to drive 
to 
over time. Following the above reasoning, we can define an equation constraint as follows to represent the speed requirement:
6.4.2 Redefinition of the Objective Function
As to 
, we examine its value in time derivative as
where 
denotes the trace of a matrix. In addition, we have 
and 
. Thus, Equation (6.14) can be simplified to
Note that
Overall, the quantity 
describes the change of 
with time. By maximizing its value, the system is enforced to evolve along the direction to increase 
gradually under the constraints. To compute 
, we first define 
for 
as follows:
with which, 
is expressed as
Incorporating this expression, Equation (6.16) becomes
For the convenience of later treatment of matrix 
, we now convert the expression of 
into a form using 
, which is the vectorization of the matrix 
formed by stacking the columns of 
into a single column vector. We have
With this, Equation (6.19) further becomes
Note that
To simplify the notation, we define a new operator 
to capture the operation in (6.22) on matrices 
, 
, …, 
and 
as below
where the second equality is obtained as follows: recall the equation 
holds for matrices 
, 
and 
of proper sizes. Setting 
, 
and 
for 
in this equation with 
being the 
identity matrix, we thus have 
. In addition, recall the transposition rule over Kronecker product as 
, with which we conclude 
.
With the notation defined in (6.23) and the relation (6.22), Equation (6.21) is converted to
The above expression involves the matrix inversion 
, which is usually time‐consuming for online computation. In order to avoid this operation, we treat this quantity as a variable and embed it into the solution procedure. To proceed, we re‐examine the definition of matrix inverse, which gives the following for 
:
Setting 
, 
, 
, equality (6.25) is converted to
6.4.3 Set Constraint
Due to physical constraints, the angular velocity of a manipulator cannot exceed certain limits, expressed as
where 
and 
are the lower and the upper bounds of 
, respectively. The bound expression (6.27) can also be expressed as a convex set constraint:
where the convex set 
is defined as
For a redundant manipulator with kinematics (6.11) and a given desired workspace velocity 
, the goal of kinematic redundancy resolution is to find a real‐time control law 
such that the workspace velocity error 
converges to zero, and the joint angular velocity converges to the convex constraint set 
as in (6.28).
6.4.4 Reformulation and Convexification
Define a new variable 
, as an estimation of 
, to replace the expression of 
in Equations (6.24) and (6.26). Then, the manipulability optimization in speed level is formulated as
It is noteworthy that the term 
is non‐negative and independent of the decision variables 
and 
. Therefore, it is equivalent to change the objective function to 
. In addition, note that the objective function in (6.30) is bilinear but is nonconvex relative to the decision variables. We incorporate one extra term 
to regulate the kinematic energy consumption. Additionally, we augment the objective function with the equality constraints (6.30b) and (6.30c) to convexify the objective function as
where 
, 
, 
, and 
are constants. Note that this new objective function is quadratic relative to 
and 
with 
being a cross term. Now, the reformulated optimization problem can be summarized as
So far, the redundancy resolution for manipulability optimization has been formulated as a constrained quadratic programming problem. However, the solution to the optimization problem (6.30) cannot be obtained directly.
6.5 Neural Networks for Redundancy Resolution
In this section, we consider developing neural dynamics for real‐time solution of the optimal manipulability redundancy resolution problem (6.32). We first convert the problem into the solution of a nonlinear equation set and then establish neural dynamics for solving this nonlinear equation set.
6.5.1 Conversion to a Nonlinear Equation Set
To solve (6.32), we first convert it into a set of nonlinear equations. Define a Lagrange function as follows:
According to the Karush–Kuhn–Tucker condition [59], the solution of (6.32) has to satisfy the following
where 
denotes the normal cone of set 
at 
. Equation (6.34) includes normal cone operation 
in its expression. It can also be equivalently written in the following form with the aid of projection operators:
i.e.
Together with 
in (6.34), and the equation constraints in (6.32), the nonlinear equations for the optimization problem (6.32) can be summarized as
The above derivation can be summarized in the following lemma.
6.5.2 Neural Dynamics for Real‐Time Redundancy Resolution
So far, we have converted the manipulability optimization problem into a nonlinear equation one. However, solving (6.37), due to its inherent nonlinearity, is a time‐consuming task and usually is hard to implemented in real time. Additionally, notice that the nonlinear equation set (6.37) is in nature a time‐varying system and its solution thus also varies with time. How to find the solution of (6.37) efficiently and keep track of it with time is a challenging problem. In this section, we present a dynamic neural network, which is able to address the problem recurrently.
For the nonlinear equation set (6.37), we construct a dynamic neural network, as described by the following ordinary differential equations with the equilibrium point identical to (6.37), to solve the redundancy resolution problem:
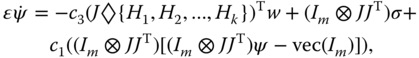
where scaling factor 
.
The architecture of the proposed dynamic neural network (6.39) is shown in Figure 6.1 for the situation with 
, 
, (
is the dimension of workspace, 
is the number of joint angle of a PUMA 560 redundant robot manipulator investigated in the ensuing simulations). From this figure, it is clear that the neural network is organized in a one‐layer architecture, which is composed of 
neurons, and is a nonlinear layer with dynamic feedback. This layer of neurons is associated with the state variables 
, 
, 
, and 
, and gets input from 
. It follows ((6.39)a), ((6.39)b), ((6.39)c), and ((6.39)d) for dynamic updates and maps the state variables to the output, which is the joint velocity 
of the robot manipulator.
Figure 6.1 Neural network architecture.
6.5.3 Convergence Analysis
This section proves stability and convergence on the proposed neural network (6.39) via the following theorem.
6.6 Illustrative Examples
In this section, computer simulations are conducted on a PUMA 560 manipulator to demonstrate the effectiveness of the proposed manipulability optimization scheme (6.32) as well as its dynamical neural network solver (6.39). Being an articulated manipulator with six independently controlled joints, the PUMA 560 can reach any position in its workspace at any orientation via its end effector. In the following simulations, we consider only the three‐dimensional position control of the end‐effector, and thus, the PUMA 560 can be deemed as a redundant manipulator for this particular task.
6.6.1 Manipulability Optimization via Self Motion
In this subsection, we perform simulations via self motion of a PUMA 560 manipulator, i.e. by using different schemes to drive the manipulator from one state with low manipulability to another state with high manipulability and without moving the end‐effector in Cartesian space. With parameters being set as 
, 
, 
, 
, 
and the rest being initially set as 0 (e.g. 
), a typical simulation run from a random initialization is generated as shown in Figures 6.2 and 6.3. Specifically, as illustrated in Figure 6.2a, the manipulator adjusts its state with the end‐effector being unmoved. As shown in Figure 6.2b, the manipulability measure 
of the PUMA 560 manipulator increases to 0.17, which means that the proposed manipulability optimization scheme (6.32) is effective. The corresponding simulation results of the detailed joint‐angle, joint‐velocity and position‐error profiles for the manipulability optimization of the PUMA 560 via self motion are illustrated in Figure 6.3. It can be seen from Figure 6.3 that, after a short‐time adjustment, the joint angle 
of the PUMA 560 converges to a constant value in Figure 6.3a, and correspondingly the joint velocity 
approaches zero as shown in Figure 6.3b. The control error 
, where 
represents the reference position in workspace, approaches zero with time as shown in Figure 6.3c. Overall, as shown in Figures 6.2 and 6.3, the manipulability optimization of the PUMA 560 manipulator via self motion synthesized by the proposed manipulability optimization scheme (6.32) as well as its dynamical neural network solver (6.39) are illustrated.
Figure 6.2 Simulation results on (a) motion trajectories and (b) manipulability measures for the manipulability optimization of PUMA 560 manipulator via self motion with its end‐effector fixed at [0.55, 0, 1.3] m in the workspace.
Figure 6.3 Simulation results of (a) joint‐angle, (b) joint‐velocity and (c) position‐error profiles for the manipulability optimization of PUMA 560 manipulator via self motion with its end‐effector fixed at [0.55, 0, 1.3] m in the workspace.
In addition, as a comparison, simulation results of the PUMA 560 manipulator synthesized by the scheme presented in [72] are illustrated in Figure 6.4. With all the parameters being same as those in the simulations shown in Figures 6.2 and 6.3, the PUMA 560 manipulator does not move and its manipulability keeps at the value of 0.091. In summary, these simulation results demonstrate the effectiveness of the proposed manipulability optimization scheme (6.32) in the increase of the manipulability as well as the singularity avoidance.
Figure 6.4 Simulation results of (a) motion trajectories, (b) manipulability measures and (c) joint‐angle profiles of PUMA 560 synthesized by the scheme presented in [72] with its end‐effector fixed at [0.55, 0, 1.3] m in the workspace.
6.6.2 Manipulability Optimization in Circular Path Tracking
In this section, computer simulations synthesized by the proposed manipulability optimization scheme (6.32) are conducted to track a circular path. Specifically, the reference position of the PUMA 560's end‐effector moves at an angular speed of 0.2 rad/s along a circle centered at 
m with radius 0.2 m and a revolution angle of 
around the 
axis. In addition, the parameters are set as 
, 
, 
, 
, 
with the rest being initially set as 0 (e.g. 
). A typical simulation run, as shown in Figure 6.5, can be generated using the proposed manipulability optimization scheme (6.32) starting from a random initial configuration. As shown in Figure 6.5a, the end‐effector of the PUMA 560 manipulator tracks the circular path successfully in the three‐dimensional work‐plane with its initial position being not on the desired path. The manipulability measures and position‐error profiles are illustrated in Figure 6.5b, from which we can observe that the manipulator is always away from singularity and the position error converges to zero after a short‐time transient. In addition, the joint angle 
varies with time in Figure 6.5c. As shown in Figure 6.5d, the joint velocity 
is kept within the limits. These results verify the effectiveness of our method.
Figure 6.5 Simulation results of PUMA 560 for tracking a circular path in the workspace synthesized by the proposed scheme (6.32). (a) Motion trajectories; (b) manipulability measures; (c) joint‐angle profiles; and (d) joint‐velocity profiles.
6.6.3 Comparisons
In this section, we compare the proposed manipulability optimization scheme (6.32) with existing solutions for tracking control of redundant manipulators presented in [70, 72, 83–85]. The scheme presented in [72] extends results in [85] from an equivalent relationship viewpoint on the velocity‐level redundancy resolution and acceleration‐level resolution. In this chapter, we focus on the velocity‐level resolution and the proposed manipulability optimization scheme (6.32) that applies to it. The proposed scheme in this chapter is able to deal with the manipulability optimization problem in an inverse‐free manner, while existing ones [70, 72, 83–85] cannot handle such a knotty problem. In addition, due to the lack of direct position feedback in [72, 85], the initialization of the manipulator's end‐effector is strictly restricted to the desired position on the desired path. Moreover, another major difference is that the proposed scheme (6.32) always maximizes the manipulability of the manipulators, while others show less satisfying performance.
It also can be observed from Figure 6.6 that, for the situation of well‐conditioned Jacobian matrix, the total computational time related to the proposed scheme (6.32) is 2.7 s, which is longer than that of the rest. This is because that extra effort is paid for by the optimization of manipulability. The total computational time of scheme (6.32) is much shorter than the task duration (i.e. 50 s), which means that such a scheme can be employed to the online solution of motion generation of redundant robot manipulators. In addition, it was found in our experiment that, for the situation of almost singular Jacobian matrix, the scheme presented in [83] uses 1029 s to fulfill the task, much longer than the task duration (i.e. 50 s), which means that such a scheme cannot be employed for the online solution of motion generation of redundant robot manipulators. By contrast, the total computational time related to scheme (6.32) is 12.4 s, which is much shorter due to the avoidance of time‐consuming matrix inversion when the matrix is almost singular. It is also noteworthy that as the benefit of manipulability optimization, the proposed scheme can quickly solve the control action while others without optimizing manipulability have to update control actions frequently when their Jacobian reaches singular, resulting in the proposed scheme consuming less time than those without manipulability optimization [72, 84, 85]. Moreover, it can be observed in our experiment that, for the situation of singular Jacobian matrix, the scheme presented in [83] cannot fulfill such a given path‐tracking task, which is mainly because of the real‐time matrix‐inversion operation involved in the scheme. Therefore, this scheme fails when encountering a singular Jacobian matrix. By contrast, as shown in our experiment, even without the ability to maximize the manipulability during the task execution process, these quadratic‐program‐based schemes presented in [72, 84, 85] could generate an approximated solution with no feasible solution at the cost of large position errors. As a quadratic‐program‐based control law designed for manipulability optimization of redundant robot manipulators in an inverse‐free manner, the proposed manipulability optimization scheme (6.32) could handle such a knotty problem in an acceptable way. That is, our scheme could always maximize the manipulability in the situation of nonsingular Jacobian matrix, and generate an approximated solution for commanding the manipulator motion in the situation of singular Jacobian matrix with superior computational efficiency and lesser position errors compared with other existing schemes.
Figure 6.6 Manipulability measures of PUMA 560 by different schemes.
Besides, it is worth comparing here the manipulability optimization scheme (6.32) and the manipulability‐maximizing scheme presented in [83], both of which are exploited to maximize the manipulability during the motion generation of redundant robot manipulators. As a basis for discussion, the manipulability optimization scheme presented in [83] is rewritten as
The reasons for the different performance of these schemes can be explained intuitively as follows: the manipulability optimization scheme (6.40) has more computational load due to the matrix inversion involved, i.e. the matrix 
has to be inverted in real time. On the contrary, the proposed manipulability optimization scheme (6.32) is able to deal with the manipulability optimization problem in an inverse‐free manner. On the one hand, for the well‐conditioned Jacobian matrix, such a matrix inversion operation can be readily done and scheme (6.40) seems to be effective in this situation. On the other hand, it is unnecessary to implement a scheme for maximizing the manipulability with well‐conditioned Jacobian matrix since the given task is far away from singularity. It is worth noting that for the matrix inversion operation existing in scheme (6.40), it would take much longer than scheme (6.32) to compute the inverse of an almost singular Jacobian matrix, which may violate real‐time requirements on the motion generation of redundant robot manipulators. What is worse, for the situation of singular Jacobian matrix, the manipulability optimization scheme (6.40) cannot work since there does not exist the inverse of a singular matrix. Note that as long as one eigenvalue of the matrix 
is zero, scheme (6.40) would fail to complete the task. However, the proposed manipulability optimization scheme (6.32) can handle such a knotty problem.
6.7 Summary
In this chapter, we have established a dynamic neural network for recurrent calculation of manipulability‐maximal control actions for redundant manipulators under physical constraints in an inverse‐free manner. By expressing position tracking and matrix inversion as equality constraints, physical limits as inequality constraints, and velocity‐level manipulability, which is affine to the joint velocities, as the objective function, the manipulability optimization scheme has been further formulated as a constrained quadratic program. Then, a dynamic neural network with rigorously provable convergence has been constructed to solve such a problem online. Computer simulations show that compared with existing methods the proposed scheme can raise the manipulability by 40% on average, which substantiates the efficacy, accuracy and superiority of the proposed scheme.