21
Quantitative Techniques: For Optimization in Logistics
After reading the chapter, the students should be able to understand:
- Role of quantitative techniques (QTs) in decision making
- Application of various quantitative techniques in logistics
- Optimization of resources using QTs
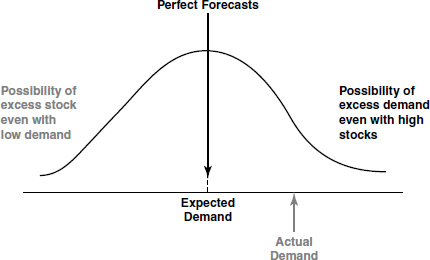
The importance of quantitative techniques (QTs) in managerial decision making is widely acknowledged. QTs for decision making are examples of using scientific methods for solving complex management problems. QTs are used for cost reduction, servicing customers and, finally, assist in decision making of business process optimization. QTs provide a tool for scientific analysis and enable proper deployment of resources by optimum allocations, help in minimizing waiting time and reduce costs. Quantitative techniques are actively and profitably used by a variety of business organizations in solving complex problems in the areas of marketing, transportation, warehousing, inventory, operations and so on.
“Statistics are like a bikini. What they reveal is suggestive, but what they conceal is vital”
—Aaron Levenstein
21.1 INTRODUCTION
Decision making is an essential and a major part of the management process. The manager, while carrying out the management functions such as planning, organizing, directing and controlling, is continuously engaged in the process of decision making. In making decisions, the management attempts to choose a course of action that is most effective under the given circumstances as well as in line with the goals of the organization. The situations a manager may face are:
- Decisions under certainty or uncertainty of the facts with variation in the probability of happening of an event
- Decisions for one time period (static) or for several time periods (dynamic) based on several interrelated facts
- Decisions under reactive market forces
The quantitative analysis approach for decision making is a process consisting of steps such as formulation of problems, determining assumptions, model building, collecting data, solving the model, interpreting results, validating the model, implementing the solutions and concluding the results. In today’s context, the market, as well as competition in business, is widening. This combines with increasing pressure from customers in terms of their requirements and expectations. Owing to the increasing complexity and rapid changes, information needs of managers are also becoming more complex and demanding in nature. With the dynamic market environment, the time available to managers to assess, analyze and react to a problem or opportunity is much reduced. Hence, for speeding the decision-making process, QTs have a major role to play. The following are a few examples where such techniques have produced large benefits by way of reduction in cost and time:
- Airlines have developed a number of quantitative models in relation to the U.S. airline seat reservation system, contributing huge profits to their revenue
- Quantitative models for fuel distribution to their retail outlets (petrol pumps) are invariably developed by petroleum manufacturers in a cost-effective way by route planning, resulting in transportation cost optimization
- “Milk runs” by the dairy industry (Amul) to collect fresh milk from a large number of farmers spread over a wide geographical area, with the limitation that the collected milk should reach the processing plant within 8 hours of collection and ensuring at the same time that tanker trucks are 100 per cent utilized
- Allocation of airline crew to flight schedules for optimum utilization of both available aircrafts and services of the crew members on roll in service scheduling
The quantitative techniques in logistics, production and the supply chain are used for route planning, transportation, trans-shipments, task assignments, inventory management, capacity planning and replacement.
21.2 FORECASTING MODELS
A forecast is an estimate of the future level of some variable. The variable is most often demand, but can also be supply or price. Forecasting is often the very first step organizations must go through when determining long-term capacity needs, yearly business plans, short-term operations and supply chain activities. It would be worthwhile to consider the following points before developing a forecasting model:
- Availability of quantitative historical data
- Evidence of a relationship between the variables
- Evidence of some variable seen as a function of time
- Evidence of some variable seen as a function of variables other than time
Forecasting is used in business planning to organize and then commit resources to achieve business goals. As the environmental forces change continuously, the parameters affecting the position of an organization in the market need to be forecast for various planning processes. Following are a few mathematical models used for forecasting.
Correlation Analysis
Correction analysis is used to measure the strength of the association between quantitative variables. For example, we could measure the degree of relationship between the distance of shipments and the corresponding charge, the examination result and the number of hours devoted in revision and so forth. The strength of a relationship between two sets of data (sample) is usually measured by the correlation coefficient, r,
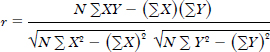
where N is the sample size and − 1 ≤ r ≤ 1.
A relation is said to be a perfect positive correlation when r = 1 and a perfect negative correlation when r = −1. The correlation analysis is one way of measuring the variance of a simple linear regression model. The scatter plots and the least-squares lines in Figure 21.1 illustrate three different types of association between variables.
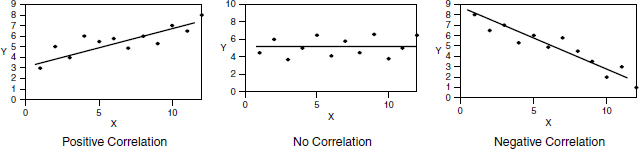
Fig. 21.1 Correlation analysis
The data about promotional expenses and sales are required to be checked for correlation (see Table 21.1).
The graphical representation of the data in Table 21.1 shows evidence of correlation between the above two variables (see Figure 21.2).
Table 21.1 Promotional Expenses and Sales Data

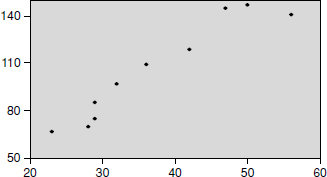
Fig. 21.2 A graphical representation of the data in Table 21.1
The correlation coefficient using the above formula works out to 0.96, which means that the two variables are highly correlated.
Time Series Forecasting Models
The dependent variable has a relationship with time period. The various models used are:
- Last period model
- Moving average model
- Weighted moving average model
- Exponential smoothing model
- Simple linear regression model (least-squares method)
The most commonly used model is the linear regression model, which is suitable for time series data that contain a trend. Linear regression is a statistical technique that expresses the forecast variable as a linear function of some independent variable. In time series modelling, the independent variable is the time period. The model (least-squares regression equation) is
where
ŷ = forecast for dependent variable, y
x = independent variable, x, used to forecast y
â = estimated intercept term for the straight line
![]() = estimated slop coefficient for the straight line
= estimated slop coefficient for the straight line
(xi, yi) = observed values for time period i
ӯ = average y value
x̄ = average x value
n = number of observations
Once the equation of the straight line is obtained, the forecast value ŷ can be calculated by putting in values of x.
21.3 LINEAR PROGRAMMING
Linear programming (LP) is the central tool of mathematical programming. LP models are flexible enough to adequately describe many realistic problems arising in modern industrial settings, while at the same time take advantage of the considerable expertise in computational linear algebra that has been developed during the last 50 years. As a result, LP models are abundantly used in logistics, transportation, finance and many other practical applications.
LP has undergone profound changes during the past 20 years, resulting in codes that are thousands (and sometimes millions) of times faster than those available just 15 years ago. Yet difficult challenges persist in the form of large-scale linear programming problems arising in routing, network design, chip design and other settings. In fact, large problem instances render even the best of codes nearly unusable.
LP was a mathematical model developed during the Second World War to plan expenditure and returns in a manner so as to reduce costs to the army and increase losses to the enemy. It was kept secret till 1947. In the post-WWII period many industries found its use in their daily business planning. Many practical problems in operations research can be expressed as LP problems. The examples are network flow problem and multi-commodity flow problems. These are considered important enough to have generated much research on specialized algorithms for their solutions. LP is heavily used in microeconomics and business management, either to maximize income or minimize costs of production schemes. Some other problems that can be expressed as LP problems are in the areas of food blending, inventory management, portfolio management, resource allocations (human and machine), business planning and advertisement campaigns. LP will have the following structure:
- A single and well-defined objective with a set of decision variables (i.e., maximum profit or minimum cost)
- A set of constraints including non-negative constraints (i.e., representations of a limited supply of resources)
- More than one solution to the problem exists (there are an infinite number of solutions)
- The objective and constraints are in the form of linear equations or inequalities
A linear function to be maximized, for example,
Problem constraints of the following formalities, for example,
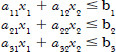
Non-negative variable, for example,
The problem usually expressed in matrix form then becomes
Other forms such as minimization problems, problems with constraints on alternative forms and problems involving variables can always be written into an equivalent problem in standard formats and solved through LP.
EXERCISE ON LINEAR PROGRAMMING
A cargo plane has three compartments for storing cargo: front, centre and rear. These compartments have the following limits on both weight and space:
| Compartment | Weight capacity (tonnes) | Space capacity (cubic metres) |
|---|---|---|
Front |
12 |
3700 |
Centre |
14 |
9800 |
Rear |
7 |
2300 |
Furthermore, the weight of the cargo in the respective compartments must be the same proportion of that compartment’s weight capacity to maintain the balance of the plane. The following four cargoes are available for shipment on the next flight:

Any proportion of these cargoes can be accepted. The objective is to determine how much (if any) of each cargo C1, C2, C3 and C4 should be accepted and how to distribute each among the compartments so that the total profit for the flight is maximised. Formulate the above problem as a linear program. What assumptions are made in formulating this problem as a linear program?
Solution
- Variables—We need to decide how much of each of the four cargoes to put in each of the three compartments. Hence let:
xij be the number of tonnes of cargo i (i = 1, 2, 3, 4 for C1, C2, C3 and C4 respectively) that is put into compartment j (j = 1 for Front, j = 2 for Centre and j = 3 for Rear) where xij. ≥ 0, i = 1, 2, 3, 4; j = 1, 2, 3
Note here that we are explicitly told we can split the cargoes into any proportions (fractions) that we like.
- Constraints—cannot pack more of each of the four cargoes than we have available

the weight capacity of each compartment must be respected
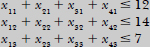
the volume (space) capacity of each compartment must be respected

the weight of the cargo in the respective compartments must be the same proportion of that compartment’s weight capacity to maintain the balance of the plane

- Objective—The objective is to maximize total profit, i.e.,

- The basic assumptions are: that each cargo can be split into whatever proportions/fractions we desire that each cargo can be split between two or more compartments if we so desire that the cargo can be packed into each compartment (for example, if the cargo was spherical it would not be possible to pack a compartment to volume capacity, some free space is inevitable in sphere packing) all the data/numbers given are accurate.
The advantages of using a software package to solve the above linear program, rather than a judgmental approach are: actually maximises profit, rather than just believing that our judgmental solution maximises profit, makes the cargo loading decision one that we can solve in a routine operational manner on a computer, rather than having to exercise judgment each and every time we want to solve it, problems that can be appropriately formulated as linear programmes are almost always better solved by computers than by people, and can perform sensitivity analysis very easily using a computer.
Thus, the LP model can be used for solving problems related to product mix, investment, scheduling, transportation and assignment of a firm.
21.4 ASSIGNMENT PROBLEMS
When a problem involves the allocation of some resources to different tasks, it comes under the purview of assignment problems. This is a special class of linear programming problem. The objective of the assignment problem is to determine the optimum assignment of given tasks that a set of workers can perform with varying efficiency, in terms of time taken and cost. If there are n tasks to perform and an equal number of persons who can do them, in varying time periods that are known, the algorithm seeks to assign the jobs to the persons in such a manner that each person gets one job and all jobs can be done in the minimum possible time. These problems can be solved by:
- Completely enumerating all possibilities and choosing the best one
- Drafting and solving the problems as linear (integer) programming problems
- Approaching them as transportation problems
- Using the Hungarian assignment method
The problem is put in a matrix form. For example, the crew members of an airline have to be assigned various flight schedules, taking into consideration their duty hours, minimum cost of overtime and availability of flights and so on. This problem can be solved by the assignment method.
Hungarian Method
- This method of solving the assignment problem requires the number of columns to be equal to the number of rows.
- When the numbers of the columns and the rows are equal, the problem is a balanced problem.
- When the above numbers are not equal, it is called an unbalanced problem.
- For example, when there are five workers and four machines or three workers and four machines, we have an unbalanced situation.
- In the case of excess machines, the machines will be idle; and workers will be idle in the case where there is an excess of them.
- In the case of an unbalanced situation, a dummy column or row is inserted; whichever is smaller in number.
- In the dummy column or row, the value placed at all places is zero.
- After putting in the dummy entry and zero values, the problem is solved in the usual manner.
Algorithm
Step 1: For the original cost matrix, identify each row’s minimum, and subtract it from all the entries of rows (i.e., row reduction).
Step 2: Using the new matrix, subtract the smallest number in each column from all other columns and again form a new matrix (i.e., column reduction).
Step 3: Check the numbers to see if there is a zero for each row and column, and draw the minimum number of lines necessary to cover all the zeros in the matrix.
Step 4: If the number of lines is equal to the number of rows, the matrix is optimal and the problem is solved.
Step 5: Optimum assignment is obtained by zero entries in the matrix.
- Example 1. Time taken by workers for various jobs is given in the following matrix. Assign the job to the worker for the optimum time.

21.5 TRANSPORTATION MODEL
Transportation problem is a special type of linear programming problem and typically involves a situation where goods are required to be transferred from some sources or manufacturing plants to some distribution centres, markets or warehouses at minimum cost. Typically in such a problem, the matrix gives the sources row-wise and the destinations are given column-wise. The unit cost of transportation from each source to each destination is provided. The purpose is to work out dispatch schedules to reduce shipping cost within the limitations of the supply and demand quantities. The transportation model can be used in other areas such as inventory control, employment scheduling and personal assignment. The transportation model can be represented as follows:
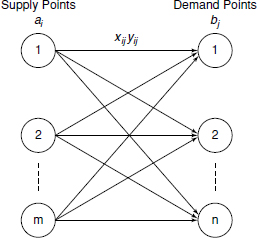
where
ai = quantity at supply point
bi = quantity at demand point
xij = transportation cost per unit from source to destination
yij = quantity shipped from source to destination
There are m sources and n destinations as shown in the model. The general form of the transportation problem in linear programming is as follows:

Even though computer solutions are used to find the optimum solution to any transportation problem, it is necessary to know the algorithms for manual computation. The methods used in manual computation are:
- Northwest corner method
- Least cost method
- Modified distribution method (stepping stone method)
Northwest Corner Rule Method
According to this rule, you start allocating quantities to cells from the top left hand corner cell. Allocate the maximum possible quantity in this cell to make allocation for a row/column complete. From this cell, move to the next row/column. Keep on allocating maximum possible quantities till the allocation is complete. Total number of “occupied cells“ must be m + n − 1, where m is the number of supply centres and n the number of demand centres.
If the number of occupied cells is less than m + n − 1, the solution is said to be “degenerate.” In such a case, assume “O” allocation to a suitable cell to make occupied cells equal to m + n − 1.
In the following example, the demand of four warehouses is fulfilled from four factories. The cost of transportation is indicated in the matrix. The logistics manager has to find out the solution for sourcing the right quantity from different factories to fulfil warehousing demand at the optimum transportation cost.

Row Minima Method
Make maximum possible allocation to the minimum cost cell in a row.
Column Minima Method
Make maximum possible allocation, column by column, to the minimum cost cell in each column.
Matrix Minima Method
Make maximum possible allocation to the minimum cost cell and proceed in the same manner for the remaining allocations.
Vogel’s Approximation Method
For every row and every column, find the difference in cost between the least-cost cell and next best least-cost cell. This difference is the penalty for failing to make an allocation to the least-cost cell. Make maximum possible allocation to the row or column where penalty is maximum. Cancel the row or column for which allocation is complete and proceed in the same manner till all allocations are complete. Vogel’s approximation method (VAM) gives a near-optimal initial feasible solution.
Distribution Method
In this method, an arbitrary initial allocation is made and it is improved upon step-by-step till the optimum schedule is reached.
Modified Distribution Method
In modified distribution (MODI) method, the test of optimality is simplified. In this method, a set of dummy row numbers S1, S2, … , Si, … , Sm and a set of dummy column numbers d1, d2, … , dj, … , dn are decided in the following manner:
Any one number is arbitrarily chosen as zero.
Then for every occupied cell, Cij = di + sj.
From this equation one can decide all numbers step by step.
Now for every unoccupied cell, the cell value is given by:
This cell value, as mentioned earlier, is the increase in cost per unit of material transported, by making an allocation to the cell. Once the cell values are known, one can make an allocation to the cell giving the maximum saving and adjusting the other allocations accordingly. The process for finding dummy numbers is a part of the test for optimality and it is repeated for every new allocation.
The negative cell value indicates incremental cost per unit, if an allocation is made to that cell. This helps in analyzing the costs, if for some reason one is constrained to make an allocation to a particular cell. If the cost of making the supply from a supply centre to a demand centre changes, the cell value will change accordingly. Thus, one can compute how much increase in cost per unit is allowed without making a cell value negative. Similarly, the effect of an increase or decrease in the capacity of a supply centre and the effect of increase or decrease in requirement of a demand centre can be worked out by analyzing changes in allocations and cell values.
In practice, there exist alternative solutions to the problems. In case the supply is not equal to the demand, introducing the dummy supply or dummy demand can solve the problem. In many situations, there always exist constraints that prohibit the use of some routes in the transportation network. In such cases, assign the number (positive or negative as the case may be) to the restricted route and carry out the algorithm. The other solution using the transportation model will be for maximizing the profit, minimizing the cost or optimizing the solution.
21.6 QUEUING THEORY
The queuing solution is suitable for solving a service-oriented problem where the customer arrives randomly to avail the service. In this service, time is a random variable. In a typical queuing situation, customers arrive to avail the service at a service system, enter a waiting line, receive service and then leave. The queuing model is relevant in service-oriented industry such as logistics, transportation, shipping, hospitality and banking. The key elements of the process are:
Source Population. Normally, all sources involve a finite or limited number of customers. In a telephone system there is a large source population. When there are many customers, usually more than 100, the source can be treated as if it were infinite in size and the number of potential customers will influence the arrival behaviour of customers for the service system.
Arrival Process. The arrival process describes the behaviour in which customers reach the service system. Customers may arrive in batches (e.g., family) or individually. Customers may also arrive on a scheduled basis (e.g., appointment with the dentist). Arrival process is measured either by arrival rate numbers per hour or inter-arrival (e.g., each visiting every 5 minutes). When service is provided on a scheduled basis, the arrival rate or inter-arrival time is fixed. In unscheduled situations, however, customers arrive in a random pattern. The random pattern in most queuing situations follows the Poisson distribution.
Waiting Line. Customers do not physically form a queue, but the queue is formed in the booking at their arrival in the system. The important factors to consider in a queuing system are size or capacity of the waiting area (customers may turn away if it is full), queue length (customer may refuse to join if it is too long) and queue organization.
Queue Discipline. The method by which customers from the waiting area are selected for service is referred to as the queue discipline. The following are queuing disciplines that can be followed:
- First-in-first-out (FIFO)
- Last-in-first-out (LIFO)
- Priority scheme
Service Process. The simplest case is a single service facility, while others may consist of multiple servers in one stage or multiple stage servers. The following are some of the examples:
- Single server, single stage
- Multiple servers, single stage
- Multiple parallel, non-identical servers, single stage
- Single server, multiple stages
- Multiple server, multiple stages
Regardless of the design configuration, it will take time to perform the service at each server. There are two ways to describe this service process:
- Service Rate—the number of customers served per unit of time, for example, 30 per hour.
- Service time—the time taken to serve a customer, for example, 2 minutes per service.
Service time may be constant (e.g., machine processing) or may fluctuate (e.g., the checkout in a supermarket) within some range of value. We can use probability distribution (e.g., negative exponential distribution) to describe the service process if it is fluctuating.
Departure. Most customers may return to the queuing system after servicing, while others may never return again.
There are several measurements that should be considered when measuring the performance of a queuing system. However, the average value of the following measurements for a system in a steady state needs to be calculated:
λ: Average arrival rate
μ: Average service rate
ρ: System utilization
Ls: Average number of customers in the queuing system
Lq: Average number of customers in the waiting line
Ws: Average time a customer spends in the system
Wq: Average time a customer spends in the waiting line
Pn: Probability of there being n customers in the queuing system.
There are two types of queuing systems, e.g. transient state (where probability of the number of customers in the system depends on time) and steady state (where probability of the number of visiting customers in the system is independent of time).
A single queue single server model is represented as (M/M/1),
where
M = Poisson arrival rate
M = Exponential service time
1 = Single server
The assumptions here are: unlimited customers, unlimited waiting area, first-come-first-served, single server, arrival rate follows a Poisson distribution, and service time follows a negative exponential distribution. The formula calculations are:

For example, a chemical company distributes its products by trucks loaded at its only loading station. The tankers of both the company and the contractor are used for this purpose. It was found that on an average every 5 minutes, one truck arrived and the average loading time is 3 minutes. Fifty per cent trucks belong to contractors. Using the queuing model and by making certain assumptions, one can find out the probability that a truck has to wait, waiting time of the truck, expected waiting time for the contractor’s truck before loading and so on.
21.7 ROUTE PLANNING
Maintaining a low-cost route structure that meets both business constraints and customer service requirements is critical to the success of a demand-driven supply chain.
For supply chain management (SCM), route planning is what you need to create the most efficient logistical routing plans to obtain the best results in asset utilisation and cost cutting. It is used to manage private/dedicated fleets and preserve a fine balance between controlling costs and providing excellent customer service. Its tactical route planning is employed to create sales territories and balance the transportation workload across multiple days. Supply chain management route planning helps companies to
- Decrease transportation and route costs
- Improve customer service
- Increase the quality of routes with reduced cross-over miles and reduced miles
SCM route planning offers sophisticated optimization, analysis and scheduling tools for choosing among a myriad of available options. It helps your team build the best daily routes for private or dedicated fleets and determine master routes, routing strategies, sales territories, service frequencies and fleet sizing, as well as analyze cost, service and profitability trade-offs. It allows you to determine the optimal route mix through route schedule construction, route schedule enhancement, asset minimization, zone design, vehicle events, service technicians and dynamic sourcing.
The routing problem refers to the problem of selecting a sequence of links on a network in a particular order. In determining the sequence of locations visited by a distribution vehicle, the routing problem is best dealt with as a discrete problem, since the many constraints to do with precedence and vehicle coverage are simple to express as constraints on routes constructed in a finite dimensional search domain. The other constraints, such as the total capacity of vehicles and time-related constraints, can be expressed as linear conditions on some appropriate variables, but can equally well be imposed on proposed solutions during a search procedure.
One of the best-known routing problems is the travelling salesman problem (TSP). The constraints of this problem are that a tour must include a number of cities, visiting each city exactly once and returning to the starting city, so that the total intercity travel cost or distance is minimum. It is possible to tackle the problem using linear inequalities (on integer-constrained variables), and then try to solve the problem through simplex-like techniques exploiting the polyhedral structure. Another commonly known problem is the vehicle routing problem (VRP). The VRP seeks to allocate some vehicles, starting from a depot to a set of demand locations, and minimize costs while satisfying other constraints (typically, total length of each tour or capacity constraints on vehicles). For these problems, one basic idea is to construct reasonable tours and then modify them, based on some savings through interchanging locations on the tour. This works well for many practical problems in logistics applications.
The VRP, with capacity constraints, is quite frequently encountered in practice; for example, in the weekly dispatches in multi-product, multi-location environments where a good service frequency is desired. It is quite often used in the local or secondary movement of goods, where frequent despatches, combined with several locations, to seek a cost-effective option. This is very common in delivery of perishables (such as milk, ice cream, vegetables), courier operations and so on.
The other common constraint in VRP is the time window constraint, which specifies a time interval during which a certain node must be visited. This makes optimal routing more difficult to obtain.
A routing problem for which an exact solution is easily available is the so-called shortest path problem. This relates to finding a sequence of nodes (from a given origin to a given destination) on a network for which the total cost is minimum. This can be done by a well-known constructive procedure called the Dijkstra’s algorithm. The other efficient procedure called Floyd’s algorithm is also used for finding the shortest path for all origin-destination pairs in route planning.
A problem that is perhaps peculiar to India is the Indian truck routing. The simplest version of this is to find a set of paths so that each path begins at a given root node, all the nodes in the network are covered by the paths and the sum of all the path lengths is minimized. The root node refers to the factory or the dispatching points and the other nodes are the demand locations.
21.8 INVENTORY MODELS
Inventory (stocks) is an integral part of every business operation. Inventories occur in all forms and for the most diverse purposes. In applications involving inventory, the manager must answer two important questions: 1. How much should be ordered? and 2. When should it be ordered?
The inventories are normally considered as goods for sales, raw materials for production, work in progress held for later production stages, and finished goods for supporting activities and customer service. They need to be controlled for being in limits before they become liabilities. For many organizations inventories are a major investment. Inventory management is an important function in many organizations even in the Internet age. The fundamental questions in inventory control are when to order and how much to order. A firm has to keep some stocks of raw materials to enable uninterrupted production operations. Depending on the nature of production operations, it may keep small or large volumes of semi-processed stocks for quick conversion to finished goods. The firm has to keep stocks of finished goods to meet the needs of customers on demand. The need for inventory depends on the following factors:
- Variations in demand for the finished goods
- Variations in production lead time and production rates
- Variations in raw material supply lead time
- Demand and capacity conditions
- Loss of customers and goodwill due to shortages or delays
There are three basic motivations for keeping inventory:
- Transaction motive: This is the desire to ensure that the business of meeting demands on time (sales) is carried out efficiently. In other words, to keep sufficient stocks so that no sale is lost and not too much stock remains unsold.
- Precautionary motive: It means the need for protection against uncertainties in demands, in lead times of production, purchase and distribution. Market demands are uncertain. Should the demand over a period be more than what was forecast, then to avoid losing the extra demand some extra (safety or buffer) stocks would be desirable. Similarly, if the lead time for receiving raw material or producing goods or distribution should be more than normal, then extra stocks would be desirable to cover the extra delays in time.
- Speculative motive: At a time of rapid changes in prices or supplies, it may be desirable to increase or decrease the stock holdings to gain some advantage. If prices are likely to fall in the near future, then stocks may be run down to the barest minimum and replenished to normal levels later availing the lower price. In contrast, if prices are likely to increase, stocks may be built up at the lower current prices; similarly, with respect to supplies, stocks may be increased or decreased.
As regards costs involved in inventory systems, there may be four different types of costs to be considered in a general inventory:
- Holding Cost: These are the costs associated with having possession of inventory, and the components are:
- Cost of money tied up in inventory (opportunity loss of capital tied up or interest paid on capital borrowed). Usually this component will be the major one, of the order of 20 per cent per year
- Cost of storing the inventory (warehouse rental/depreciation and maintenance)
- Rates, taxes and insurance
- Security
- Loss due to pilferage/shortages
- Loss due to obsolescence and deterioration
- Ordering Cost: These are costs incurred in acquiring inventory—purchase from external sources or in-house production. The components are:
- Cost of information processing on inventory status
- Cost of negotiations with suppliers
- Cost of transmission of order
- Cost associated with the receipt and inspection of stocks
- Shortage Costs: These costs are relatively more difficult to assess. Yet they may be very pertinent to the decisions on inventory.
- Cost of losing sales due to non-availability of item, that is, profit that was not earned if there could have been a sale
- Cost of back order—in case the sale is not lost, that is, the customer is prepared to wait for some time to receive the stock
- Cost of goodwill—if the firm frequently goes out of stock in the market or frequently has to back-order, in the long run the customers may not be impressed with the service and may forever be lost for all future sales potential
- Cost of Usage or Consumption: This is the total purchase cost of the items or the total cost of production.
In the study of inventory, decisions have to be taken as to:
- How much stock to buy (or produce)?—Q factor (quantity)
- When to buy or (produce)?—P factor (time)
The conditions and assumptions under which the above two decisions are taken ma vary from situation to situation. Each situation leads to a model of the inventory system Many models—from the very simple to the most complex—have been developed and studied, depending on the specific needs of the operations of the firm. These model can take the following forms:
- Q fixed, P fixed (fixed order quantity policy)
- Q fixed, P variable (regular replenishment of a fixed quantity)
- Q variable, P fixed (optional replenishment policy)
- Q variable, P variable (general replenishment policy)
Basic Stock Model—Economic Order Quantity Model (EOQ)
This is the earliest model developed. While it has a very limited use in practice, yet the model i informative to understand the interplay of factors that influence inventory decision. It can be used in certain restricted areas of purchase of general-purpose consumables where there are many sup pliers of standard products. The assumptions in EOQ model are:
- The demand for the item of inventory is known with certainty. The rate of usage of the iten is nearly constant over time
- The lead time for supply is known and constant
- Stockouts are not allowed
- Delivery of supplies is instantaneous in one lot, that is, the time to receive the stock is ver short
- The price of the item is independent of the quantity ordered. In an EOQ system the stock i very short
- The price of the item is independent of the quantity ordered. In an EOQ system the stoc] levels will repeatedly fluctuate as shown in the graph

In the literature, this formula is sometimes referred to as Wilson’s formula.
where
D: Annual usage of the item (in units)
Co: Cost of ordering (Rs. per order)
Cc: Cost of carrying (holding) (Rs. per item per year)
P: Unit price of goods (Rs. per unit)
I: Inventory-carrying cost (expressed as per cent per annum), that is, marginal rate of interest on working capital finance
Q: Order quantity
N: Number of orders per year
Q*: Optimal order quantity, that is, EOQ
In this model the total cost of consumption or usage over the year will remain constant, irrespective of the decision on the quantity Q ordered, since the Cc does not change with Q. Hence, this cost can be ignored. Since the demand is known and fixed and the lead time for receipt of stocks is also fixed, there will never be a stockout. Hence, stockout cost will not feature in the model. The two costs that will be relevant to an optimal decision are: the cost of ordering and the cost of holding. These costs can be graphically depicted as under:
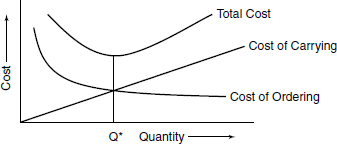
The graph clearly brings out the features of the interplay of ordering/holding costs related to order quantity Q. If Q is large, fewer orders will be required per year and the ordering cost will fall, but the quantity per order being large, the holding cost will increase.
Conversely, if the quantity Q is small, while the holding cost will fall the number of orders per year and the ordering cost will increase. At the level Q* we note that the two curves of ordering and holding costs cross (both attain equal value) to yield the minimum total cost as seen from the graph.
In the above formula for EOQ, we have used Cc as the cost of holding inventory. This is an absolute value in rupees per unit per year. In a company where there are thousands of items of inventory, it would be tedious to compile the absolute holding cost for each item.
Even if one were to do so, and if at a later time one of the components of holding cost (e.g., cost of capital or storage) were to change, then all the costs will have to be recomputed.
To avoid such a situation, it is the usual practice to use what is called an inventory-carrying rate (I), uniformly applicable to all items. It is expressed as a percentage of the cost of the item. Thus, the holding cost Cc = I · P (where P is the per unit cost of the item).
If P is large then the holding cost will also be large, and if P is small then the holding cost will be small too. We deem that each item, so to say, will bear a holding cost in proportion to its cost or value. This is partly justifiable since out of the 30 per cent cost per annum, the cost of money tied up usually accounts for 20 per cent. Thus, the EOQ formula usually used in practice is:
It can be seen from the graph of the total cost that the curve becomes nearly flat around the region of the EOQ. That is, the change in total cost will not be very significant if the order quantity Q were to be slightly different from the EOQ. Further, it can be seen that the total cost is not very sensitive to changes in D, Co or Cc. This is a very useful feature advantageous to the operation of an EOQ system.
Sensitivity analysis of EOQ is carried out at the planning stage, much before the start of the financial year. As such, the values of Co, Cc, price P and interest I are all determined on the basis of forecasting. It is quite likely that when the actual operations for the year start, the actual values of all parameters may be different.
Inventory models under uncertainty risks depend on probabilities of the occurrence of the parameters. For example, the level of safety stocks varies with probabilistic demand during lead time. In addition, service level is probability of stock availability and stockout risk (SOR) is probability of shortage. The risks are very high, when both daily demand and lead time are probabilistic.
21.9 SIMULATION
According to T.H. Taylor, “Simulation is a numerical technique for conducting experiments on digital computers, which involves certain types of mathematical and logical relationships necessary to describe the behaviour and structure of a complex real-world system over an extended period of time.” When decisions are to be taken under conditions of uncertainty, simulation can be used. Simulation provides trial and error movement towards optimal solution. Simulation as a quantitative method requires the setting up of a mathematical model that would represent the interrelationships between the variables involved in the actual situation in which a decision is to be taken. Then, a number of trials or experiments are conducted with the model to determine the results that can be expected, when the variables assume various values. Simulation can therefore be defined as a procedure whereby one can draw conclusions about the behaviour of a given system, by examining the behaviour of a corresponding model whose cause and effect relationships are similar to those in the actual system.
Simulation can serve as a “pre-test” to try out new decision rules for a system. It can anticipate problems and bottlenecks that may arise while operating a system. There are a few basic concepts that must be understood before applying the simulating techniqe.
System: It is the segment to be studied or understood to draw conclusions. In the product-market system, the market for the products together with the firm’s production process constitutes the relevant system. The variable can be identified only after defining the system. The variables that interact with one another in the system and establish their relationships mathematically are given below:
Decision Variables: Decision variables are those variables whose value is to be determined through the process of simulation.
Environmental Variables: These are the variables that describe the environment. In marketing, the environmental variables are the competitors’ average price, consumer preferences and demand and so forth.
Endogenous Variables: These variables are generated within the system itself. In the marketing context, the quantity sold, sales revenue, total cost and profit are endogenous variables.
Criterion Function: Any variable can be used as the criterion function for evaluating the performance of the system. In marketing, profit is used as the criterion function.
For example, let us assume that the competitors’ average price is Pc and the price charged by the firm is P. If the quantity sold is Q, then, as the quantity sold depends upon the firm’s price P and the competitors’ average price Pc, we can then express this relationship mathematically as:
If we assume the total cost of the quantity sold is C, then C = g(Q).
The total cost is a function of the quantity sold. If 1 t is the profit earned by the firm, then
The above equation is a mathematical model of the system. It contains (in equation form) the interrelationships among the endogenous, decision and environmental variables. This mathematical model is also the criterion function. Mathematical modelling requires the setting up of mathematical relationships that would represent the system. Although some relationships can be expressed as equations, other relationships or constraints on the criterion function may be expressed only as inequalities (as we have seen in linear programming). If the mathematical model set up could always be optimized by the analytical approach, then there would be no need for simulation. It is only when the interrelationships are too complex, or there is uncertainty regarding the values that could be assumed by the variables, or both, that we have to resort to simulation.
The Monte Carlo method is a technique that involves using random numbers and probability to solve problems. S. Ulam and Nicholas Metropolis coined the term “Monte Carlo” in reference to the games of chance that are a popular attraction in Monte Carlo, Monaco.
Computer simulation has to do with using computer models to imitate real life or make predictions. When you create a model with a spreadsheet like in Excel, you have a certain number of input parameters and a few equations that use those inputs to give you a set of outputs (or response variables). This type of model is usually deterministic, which means that you get the same results no matter how many times you recalculate.
The Monte Carlo simulation is a method for alliteratively evaluating a deterministic model using sets of random numbers as inputs. This method is often used when the model is complex, nonlinear, or involves more than just a couple of uncertain parameters. A simulation can typically involve over 10,000 evaluations of the model, a task that in the past was only practical using super computers.
By using random inputs, you are essentially turning the deterministic model into a stochastic model.
The Monte Carlo method is just one of many methods for analyzing uncertainty propagation, where the goal is to determine how random variation, lack of knowledge or error affects the sensitivity, performance, or reliability of the system that is being modelled. The Monte Carlo simulation is categorized as a sampling method, because the inputs are randomly generated from probability distributions to simulate the process of sampling from an actual population. So, we try to choose a distribution for the inputs that most closely matches data we already have, or best represents our current state of knowledge. The data generated from the simulation can be represented as probability distributions (or histograms) or converted to error bars, reliability predictions, tolerance zones and confidence intervals.
All we need to do is follow the five simple steps listed below:
Step 1: Create a parametric model, y = f(x1, x2, … , xq).
Step 2: Generate a set of random inputs, xi1, xi2, … , xiq.
Step 3: Evaluate the model and store the results as yi.
Step 4: Repeat steps 2 and 3 for i = 1 to n.
Step 5: Analyze the results using histograms, summary statistics, confidence intervals, and so on.
A model usually refers to a particular level in the managerial decision-making context and the decisions of the higher levels (if any) involving multiple variables. The process of modelling follows the managerial hierarchy of strategic, tactical and operational concerns. For example, an operational model will have certain constraints imposed by a tactical-level decision. The objective associated with the model is likely to be derived again from a higher level decision. Full-scale mathematical modelling is probably most useful for tactical decision making, with a medium time horizon under consideration, and where a certain level of aggregation of data is possible. For higher level decision making, by its very nature, data is uncertain, intangibles are many and hard modelling is unlikely to be very useful in decision making. Other options, such as soft systems modelling, some models of discrete decision analysis and cognitive maps are possibilities for strategic decision making.
For operational decisions, simple automated rule-based systems are likely to be effective, and the models used will need to be simple to validate. Fast computational procedures will be the major consideration. Information technology for decision support and automation of data processing is needed in such situations, rather than complicated models.
Models are useful to describe the interrelationships between different quantities of interest and sometimes to derive certain optimal or good policies. The models based on mathematical programming, inventory theory, routing and scheduling theory can directly address a sharp decision area, or can be part of the quantitative assessment for more aggregate decisions.
SUMMARY
Logistics refers to a process that is associated with the flow of information, goods and services offered to suppliers and customers from the point of origin to the point of destination. Logistics analysis involves the use of numerous quantitative techniques, strategic and tactical planning on the part of the organization while still giving importance to the sphere of operational research. It involves logistical aspects such as network design, forecasting, inventory control and warehousing.
Decision making is an essential and a major part of the management process. The quantitative analysis approach for decision making is the process consisting of steps such as formulation of problems, determining assumptions, model building, collecting data, solving the model, interpreting results, validating the model and implementing the solutions. The quantitative techniques in logistics and the supply chain are used for route planning, transportation, trans-shipments, task assignments, inventory management, capacity planning and replacement models, and so on. Forecasting is used in business planning to organize and then commit resources to achieve business goals. As the environmental forces change continuously, the parameters that have an effect on the position of an organization in the market need to be forecast for various planning processes. A few mathematical models such as correlation and time series models are used for forecasting.
Linear programming models are abundantly used in logistics, transportation, finance and many other practical applications. Assignment and transportation problems are solved with the linear programming technique. The routing problem refers to the problem of selecting a sequence of links on a network in a particular order. In determining the sequence of locations visited by a distribution vehicle, the routing problem is best dealt with as a discrete problem, since the many constraints to do with precedence and vehicle coverage are simple to express as constraints on routes constructed in a finite dimensional search domain. For many organizations, inventories are a major investment. Inventory management is an important function in many organizations, even in the Internet age. The fundamental questions in inventory control are, when to order and how much to order. The inventory ordering is resolved through EOQ model under conditions of certainty and uncertainty. When decisions are to be taken under conditions of uncertainty, simulation can be used. Simulation as a quantitative method requires the setting up of a mathematical model that would represent the interrelationships between the variables involved in the actual situation in which a decision is to be taken.
REVIEW QUESTIONS
- Find out the different application areas of quantitative techniques.
- “Modern-day managerial decision making uses various quantitative technique tools.” Comment on this statement mentioning the utility of at least five such tools (with examples).
- Discuss the applications of linear programming (LP) in logistics. Express LP problem in its general form and matrix notation.
- Discuss factors associated with queuing process. Also explain the concept of optimum servicing rate and optimum cost.
- Discuss how quantitative techniques are used in warehouse network planning?
INTERNET EXERCISES
- Visit http://www.profit.com and study how software is used for “Optimizing Routing and Transportation.”
- Visit http://www.opsresarch.com for knowing more about vehicle routing and modelling.
- Find out if there is a relationship between the “economic batch quantity” and the “kanban’ quantity.”
BIBLIOGRAPHY
Anderson, David R., Dennis J. Sweeney and Thomas A. Williams. 2002. Statistics for Business and Economics. 8th edition. Singapore: Thomson South Western.
Baudin, Michel. 2005. Lean Logistics: The Nuts and Bolds of Delivering Materials and Goods. New York: Productivity Press.
Beri, G.C. 2005. Business Statistics. 2nd edition. New Delhi: Tata McGraw-Hill.
Bronson, Rechard. 2002. Operations Research. Singapore: McGraw-Hill.
Frohne, Philip. T. 2007. Quantitative Measurements for Logistics. New York: McGraw-Hill Professional.
Green, Willan H. 2003. Econometric Analysis. 5th edition. Upper Saddle River, NY: Prentice Hall.
Klose, Andreas, M. Grazia Speranza and Luk N. Van Wassenhore. 2002. Quantitative Approaches to Distribution Logistics and Supply Chain. Berlin: Springer.
Nohra, V.D. 2002. Quantitative Techniques in Management. New Delhi: Tata McGrwa-Hill.
Stevenson, William J. 2005. Operations Management. 8th edition. Irwin, Boston: McGraw-Hill.
Tulsian, PC., and Vishal Pandey. 2008. Quantitative Techniques: Theory and Problem. New Delhi: Pearson Education.
Vohra, N.D. 2002. Theory and Problems in Quantitative Techniques in Management. New Delhi: Pearson Education.
Wisniewski, Mik. 1996. Quantitative Methods for Decision Makers. New Delhi: Macmillan India.
