13
Bayesian Estimation
All of the previous discussion on estimation has assumed a frequentist approach. That is, the population distribution has been fixed but unknown, and our decisions have been concerned not only with the sample we obtained from the population, but also with the possibilities attached to other samples that might have been obtained. The Bayesian approach assumes that only the data actually observed are relevant and it is the population distribution that is variable. For parameter estimation, the following definitions describe the process and then Bayes' theorem provides the solution.
13.1 Definitions and Bayes' Theorem
As before, the parameter ![]() may be scalar or vector valued. Determination of the prior distribution has always been one of the barriers to the widespread acceptance of Bayesian methods. It is almost certainly the case that your experience has provided some insights about possible parameter values before the first data point has been observed. (If you have no such opinions, perhaps the wisdom of the person who assigned this task to you should be questioned.) The difficulty is translating this knowledge into a probability distribution. An excellent discussion about prior distributions and the foundations of Bayesian analysis can be found in Lindley [80], and for a discussion about issues surrounding the choice of Bayesian versus frequentist methods, see Efron [33]. The book by Klugman [72] contains more detail on the Bayesian approach, along with several actuarial applications. More recent papers applying Bayesian methods to actuarial problems include deAlba [26], Fellingham, Kottas, and Hartman [39], Meyers [88, 89], Mildenhall [90], Ntzoufras and Dellaportas [95], Scollnik [111], Verrall [125], and Wuthrich [133]. General applications of actuarial interest can be found in Hartman [49] and Hartman, Richardson, and Bateman [50]. For a thorough mathematical treatment of Bayesian methods, a good source is the text by Berger [14]. In recent years, many advancements in Bayesian calculations have taken place. Two good reviews are Carlin and Louis [22] and Gelman et al. [42].
may be scalar or vector valued. Determination of the prior distribution has always been one of the barriers to the widespread acceptance of Bayesian methods. It is almost certainly the case that your experience has provided some insights about possible parameter values before the first data point has been observed. (If you have no such opinions, perhaps the wisdom of the person who assigned this task to you should be questioned.) The difficulty is translating this knowledge into a probability distribution. An excellent discussion about prior distributions and the foundations of Bayesian analysis can be found in Lindley [80], and for a discussion about issues surrounding the choice of Bayesian versus frequentist methods, see Efron [33]. The book by Klugman [72] contains more detail on the Bayesian approach, along with several actuarial applications. More recent papers applying Bayesian methods to actuarial problems include deAlba [26], Fellingham, Kottas, and Hartman [39], Meyers [88, 89], Mildenhall [90], Ntzoufras and Dellaportas [95], Scollnik [111], Verrall [125], and Wuthrich [133]. General applications of actuarial interest can be found in Hartman [49] and Hartman, Richardson, and Bateman [50]. For a thorough mathematical treatment of Bayesian methods, a good source is the text by Berger [14]. In recent years, many advancements in Bayesian calculations have taken place. Two good reviews are Carlin and Louis [22] and Gelman et al. [42].
Due to the difficulty of finding a prior distribution that is convincing (you will have to convince others that your prior opinions are valid) and the possibility that you may really have no prior opinion, the definition of prior distribution can be loosened.
A great deal of research has gone into the determination of a so-called noninformative or vague prior. Its purpose is to reflect minimal knowledge. Universal agreement on the best way to construct a vague prior does not exist. However, there is agreement that the appropriate noninformative prior for a scale parameter is ![]() . Note that this is an improper prior.
. Note that this is an improper prior.
For a Bayesian analysis, the model is no different than before. In our development, we will use pdf to represent discrete and mixed distributions in addition to those that are continuous. In the formulas, integrals should be replaced by sums as appropriate.
Thus, as with maximum likelihood estimation, a necessary step is the ability to write the likelihood function for the given situation. Data that have been truncated or censored can thus be analyzed by Bayesian methods. We use concepts from multivariate statistics to obtain two more definitions.
Note that if there is more than one parameter, this equation will be a multiple integral. Compare this definition to that of a mixture distribution given by (5.2) in Section 5.2.4. The final two quantities of interest are the posterior and predictive distributions.
These last two items are the key output of a Bayesian analysis. The posterior distribution tells us how our opinion about the parameter has changed once we have observed the data. The predictive distribution tells us what the next observation might look like given the information contained in the data (as well as, implicitly, our prior opinion). Bayes' theorem tells us how to compute the posterior distribution.
The predictive distribution can be interpreted as a mixture distribution, where the mixing is with respect to the posterior distribution. Example 13.1 illustrates the preceding definitions and results. The setting is taken from Meyers [87], though the data are not.
![]()
![]()
13.2 Inference and Prediction
In one sense, the analysis is complete. We begin with a distribution that quantifies our knowledge about the parameter and/or the next observation, and we end with a revised distribution. But we suspect that your boss may not be satisfied if you produce a distribution in response to his or her request. No doubt a specific number, perhaps with a margin for error, is what is desired. The usual Bayesian solution is to pose a loss function.
It is possible to have a multidimensional loss function ![]() that allows the loss to depend simultaneously on the errors in the various parameter estimates.
that allows the loss to depend simultaneously on the errors in the various parameter estimates.
The three most commonly used loss functions are defined as follows.
The following theorem indicates the Bayes estimates for these three common loss functions.
Note that there is no guarantee that the posterior mean exists or that the posterior median or mode will be unique. Further note that if the improper prior ![]() is used and the estimate is the posterior mode, then the estimate will match the maximum likelihood estimate. When not otherwise specified, the term Bayes estimate refers to the posterior mean.
is used and the estimate is the posterior mode, then the estimate will match the maximum likelihood estimate. When not otherwise specified, the term Bayes estimate refers to the posterior mean.
![]()
For forecasting purposes, the expected value of the predictive distribution is often of interest. It can be thought of as providing a point estimate of the ![]() observation given the first n observations and the prior distribution. It is
observation given the first n observations and the prior distribution. It is
Equation (13.5) can be interpreted as a weighted average, using the posterior distribution as the weights.
![]()
The Bayesian equivalent of a confidence interval is easy to construct. The following definition suffices.
The use of the term credibility has no relationship to its use in actuarial analyses as developed in Chapter 16.
The inequality is present for the case where the posterior distribution of ![]() is discrete. Then it may not be possible for the probability to be exactly
is discrete. Then it may not be possible for the probability to be exactly ![]() . This definition does not produce a unique solution. The following theorem indicates one way to produce a unique interval.
. This definition does not produce a unique solution. The following theorem indicates one way to produce a unique interval.
The following example may clarify the theorem.
![]()
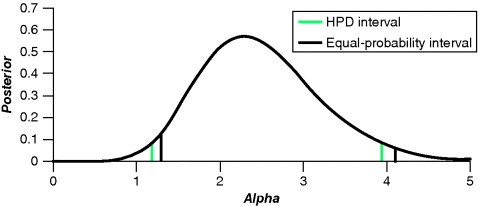
Figure 13.1 Two Bayesian credibility intervals.
The following definition provides the equivalent result for any posterior distribution.
This set may be the union of several intervals (which can happen with a multimodal posterior distribution). This definition produces the set of minimum total width that has the required posterior probability. Construction of the set is done by starting with a high value of c and then lowering it. As it decreases, the set C gets larger, as does the probability. The process continues until the probability reaches ![]() . It should be obvious to see how the definition can be extended to the construction of a simultaneous credibility region for a vector of parameters,
. It should be obvious to see how the definition can be extended to the construction of a simultaneous credibility region for a vector of parameters, ![]() .
.
Sometimes it is the case that, while computing posterior probabilities is difficult, computing posterior moments may be easy. We can then use the Bayesian central limit theorem. The following theorem is paraphrased from Berger [14, p. 224].
The “commonly satisfied assumptions” are like those in Theorem 11.4. As in that theorem, it is possible to do further approximations. In particular, the asymptotic normal distribution also results if the posterior mode is substituted for the posterior mean and/or if the posterior covariance matrix is estimated by inverting the matrix of second partial derivatives of the negative logarithm of the posterior density.
![]()
The same concepts can apply to the predictive distribution. However, the Bayesian central limit theorem does not help here because the predictive sample has only one member. The only potential use for it is that, for a large original sample size, we can replace the true posterior distribution in (13.2) with a multivariate normal distribution.
![]()
The following example revisits a calculation done in Section 6.3. There, the negative binomial distribution was derived as a gamma mixture of Poisson variables. Example 13.8 shows how the same calculations arise in a Bayesian context.
![]()
When only moments are needed, the double-expectation formulas can be very useful. Provided that the moments exist, for any random variables X and Y,
For the predictive distribution,
and
The simplification on the inner expected value and variance results from the fact that, if ![]() is known, the value of x provides no additional information about the distribution of Y. This is simply a restatement of (13.5).
is known, the value of x provides no additional information about the distribution of Y. This is simply a restatement of (13.5).
![]()
13.2.1 Exercises
- 13.1 Show that, if Y is the predictive distribution in Example 13.1, then
 has a Pareto distribution.
has a Pareto distribution. - 13.2 Determine the posterior distribution of
 in Example 13.1 if the prior distribution is an arbitrary gamma distribution. To avoid confusion, denote the first parameter of this gamma distribution by
in Example 13.1 if the prior distribution is an arbitrary gamma distribution. To avoid confusion, denote the first parameter of this gamma distribution by  . Next, determine a particular combination of gamma parameters so that the posterior mean is the maximum likelihood estimate of
. Next, determine a particular combination of gamma parameters so that the posterior mean is the maximum likelihood estimate of  regardless of the specific values of
regardless of the specific values of  . Is this prior improper?
. Is this prior improper? - 13.3 Let
 be a random sample from a lognormal distribution with unknown parameters
be a random sample from a lognormal distribution with unknown parameters  and
and  . Let the prior density be
. Let the prior density be  .
.
- Write the posterior pdf of
 and
and  up to a constant of proportionality.
up to a constant of proportionality. - Determine Bayesian estimators of
 and
and  by using the posterior mode.
by using the posterior mode. - Fix
 at the posterior mode as determined in part (b) and then determine the exact (conditional) pdf of
at the posterior mode as determined in part (b) and then determine the exact (conditional) pdf of  . Then use it to determine a 95% HPD credibility interval for
. Then use it to determine a 95% HPD credibility interval for  .
.
- Write the posterior pdf of
- 13.4 A random sample of size 100 has been taken from a gamma distribution with
 known to be 2, but
known to be 2, but  unknown. For this sample,
unknown. For this sample,  . The prior distribution for
. The prior distribution for  is inverse gamma, with
is inverse gamma, with  taking the role of
taking the role of  and
and  taking the role of
taking the role of  .
.
- Determine the exact posterior distribution of
 . At this point, the values of
. At this point, the values of  and
and  have yet to be specified.
have yet to be specified. - The population mean is
 . Determine the posterior mean of
. Determine the posterior mean of  using the prior distribution first with
using the prior distribution first with  [this is equivalent to
[this is equivalent to  ] and then with
] and then with 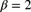 and
and  (which is a prior mean of 250). Then, in each case, determine a 95% credibility interval with 2.5% probability on each side.
(which is a prior mean of 250). Then, in each case, determine a 95% credibility interval with 2.5% probability on each side. - Determine the posterior variance of
 and use the Bayesian central limit theorem to construct a 95% credibility interval for
and use the Bayesian central limit theorem to construct a 95% credibility interval for 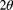 using each of the two prior distributions given in part (b).
using each of the two prior distributions given in part (b). - Determine the maximum likelihood estimate of
 and then use the estimated variance to construct a 95% confidence interval for
and then use the estimated variance to construct a 95% confidence interval for  .
.
- Determine the exact posterior distribution of
- 13.5 Suppose that, given
 , the random variables
, the random variables  are independent and binomially distributed with pf
are independent and binomially distributed with pf

and
 itself is beta distributed with parameters a and b and pdf
itself is beta distributed with parameters a and b and pdf
- Verify that the marginal pf of
 is
is

and
 . This distribution is termed the binomial–beta or negative hypergeometric distribution.
. This distribution is termed the binomial–beta or negative hypergeometric distribution. - Determine the posterior pdf
 and the posterior mean
and the posterior mean  .
.
- Verify that the marginal pf of
- 13.6 Suppose that, given
 , the random variables
, the random variables  are independent and identically exponentially distributed with pdf
are independent and identically exponentially distributed with pdf

and
 is itself gamma distributed with parameters
is itself gamma distributed with parameters  and
and  ,
,
- Verify that the marginal pdf of
 is
is

and

This distribution is one form of the Pareto distribution
. - Determine the posterior pdf
 and the posterior mean
and the posterior mean  .
.
- Verify that the marginal pdf of
- 13.7 Suppose that, given
 , the random variables
, the random variables  are independent and identically negative binomially distributed with parameters r and
are independent and identically negative binomially distributed with parameters r and  with pf
with pf

and
 itself is beta distributed with parameters a and b and pdf
itself is beta distributed with parameters a and b and pdf
- Verify that the marginal pf of
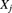 is
is

and

This distribution is termed the generalized Waring distribution. The special case where
 is the Waring distribution and is the Yule distribution if
is the Waring distribution and is the Yule distribution if  and
and  .
. - Determine the posterior pdf
 and the posterior mean
and the posterior mean  .
.
- Verify that the marginal pf of
- 13.8 Suppose that, given
 , the random variables
, the random variables  are independent and identically normally distributed with mean
are independent and identically normally distributed with mean  and variance
and variance  , and
, and  is gamma distributed with parameters
is gamma distributed with parameters  and (
and ( replaced by)
replaced by)  .
.
- Verify that the marginal pdf of
 is
is
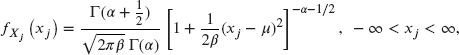
which is a form of the t-distribution.
- Determine the posterior pdf
 and the posterior mean
and the posterior mean  .
.
- Verify that the marginal pdf of
- 13.9 Suppose that, for
 , the random variable
, the random variable 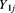 has (conditional on
has (conditional on  ) the Poisson pf
) the Poisson pf
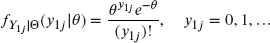
and
 has (conditional on
has (conditional on  ) the binomial pf
) the binomial pf
with
 and N a known positive integer. Further assume that all random variables are independent (conditional on
and N a known positive integer. Further assume that all random variables are independent (conditional on  ). Let
). Let 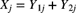 for
for  .
.- Show that
 has (conditional on
has (conditional on  ) the Poisson–binomial pf
) the Poisson–binomial pf

where

- If
 have the pf in (a), demonstrate that the conjugate prior for this situation is
have the pf in (a), demonstrate that the conjugate prior for this situation is

where
 and
and  . Show further that
. Show further that
where
 is the confluent hypergeometric function of the second kind, which can be expressed as
is the confluent hypergeometric function of the second kind, which can be expressed as
- Show that
- 13.10 Suppose that, given N, the random variable X is binomially distributed with parameters N and p.
- Show that, if N is Poisson distributed, so is X (unconditionally) and identify the parameters.
- Show that, if N is binomially distributed, so is X (unconditionally) and identify the parameters.
- Show that, if N is negative binomially distributed, so is X (unconditionally) and identify the parameters.
- 13.11 (*) A die is selected at random from an urn that contains two six-sided dice. Die number 1 has three faces with the number 2, while one face each has the numbers 1, 3, and 4. Die number 2 has three faces with the number 4, while one face each has the numbers 1, 2, and 3. The first five rolls of the die yielded the numbers 2, 3, 4, 1, and 4, in that order. Determine the probability that the selected die was die number 2.
- 13.12 (*) The number of claims in a year, Y, has a distribution that depends on a parameter
 . As a random variable,
. As a random variable,  has the uniform distribution on the interval (0,1). The unconditional probability that Y is 0 is greater than 0.35. For each of the following conditional pfs, determine if it is possible that it is the true conditional pf of Y:
has the uniform distribution on the interval (0,1). The unconditional probability that Y is 0 is greater than 0.35. For each of the following conditional pfs, determine if it is possible that it is the true conditional pf of Y:
 .
. .
. .
.
- 13.13 (*) Your prior distribution concerning the unknown value of H is
 and
and 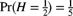 . The observation from a single experiment has distribution
. The observation from a single experiment has distribution 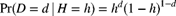 for
for  . The result of a single experiment is
. The result of a single experiment is  . Determine the posterior distribution of H.
. Determine the posterior distribution of H. - 13.14 (*) The number of claims for an individual in one year has a Poisson distribution with parameter
 . The prior distribution for
. The prior distribution for  has a gamma distribution with mean 0.14 and variance 0.0004. During the past two years, a total of 110 claims has been observed. In each year, there were 310 policies in force. Determine the expected value and variance of the posterior distribution of
has a gamma distribution with mean 0.14 and variance 0.0004. During the past two years, a total of 110 claims has been observed. In each year, there were 310 policies in force. Determine the expected value and variance of the posterior distribution of  .
. - 13.15 (*) An individual risk has exactly one claim each year. The amount of the single claim has an exponential distribution with pdf
 . The parameter t has a prior distribution with pdf
. The parameter t has a prior distribution with pdf  . A claim of 5 has been observed. Determine the posterior pdf of t.
. A claim of 5 has been observed. Determine the posterior pdf of t. - 13.16 (*) Given
 ,
,  are i.i.d. Bernoulli random variables with parameter q. Let
are i.i.d. Bernoulli random variables with parameter q. Let  . The prior distribution of Q is beta with
. The prior distribution of Q is beta with  ,
,  , and
, and  . Determine the smallest value of m such that the mean of the marginal distribution of
. Determine the smallest value of m such that the mean of the marginal distribution of  is greater than or equal to 50.
is greater than or equal to 50. - 13.17 (*) Given
 , a loss X has the exponential pdf
, a loss X has the exponential pdf  ,
,  . The prior distribution is
. The prior distribution is  ,
,  , an inverse gamma distribution. A single loss of x has been observed. Determine the mean of the posterior distribution as a function of x.
, an inverse gamma distribution. A single loss of x has been observed. Determine the mean of the posterior distribution as a function of x. - 13.18 In Exercise 11.24, 500 losses are observed. Five of the losses are 1,100, 3,200, 3,300, 3,500, and 3,900. All that is known about the other 495 losses is that they exceed 4,000. Determine the Bayes estimate of the mean of an exponential model using the improper prior
 and compare your answer to the maximum likelihood estimate.
and compare your answer to the maximum likelihood estimate. - 13.19 Suppose that, given
 and
and  , the random variables
, the random variables  are independent and identically normally distributed with mean
are independent and identically normally distributed with mean  and variance
and variance  . Suppose also that the conditional distribution of
. Suppose also that the conditional distribution of  given
given  is a normal distribution with mean
is a normal distribution with mean  and variance
and variance  and
and  is gamma distributed with parameters
is gamma distributed with parameters  and
and  .
.
- Show that the posterior conditional distribution of
 given
given 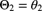 is normally distributed with mean
is normally distributed with mean

and variance
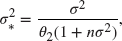
and the posterior marginal distribution of
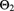 is gamma distributed with parameters
is gamma distributed with parameters
and

- Find the posterior marginal means
 and
and  .
.
- Show that the posterior conditional distribution of
13.3 Conjugate Prior Distributions and the Linear Exponential Family
The linear exponential family introduced in Section 5.4 is also useful in connection with Bayesian analysis, as is demonstrated in this section.
In Example 13.8, it turned out the posterior distribution was of the same type as the prior distribution (gamma). A definition of this concept follows.
The following theorem shows that, if the model is a member of the linear exponential family, a conjugate prior distribution is easy to find.
![]()
![]()
Other well-known examples of linear exponential family members include the binomial and negative binomial distributions both with beta conjugate prior (see Exercises 13.5 and 13.7, respectively). Similarly, for the exponential distribution, the gamma distribution is the conjugate prior (see Exercise 13.6).
13.3.1 Exercises
- 13.20 Let
 be i.i.d. random variables, conditional on
be i.i.d. random variables, conditional on  , with pf
, with pf

Let
 . Use Exercise 5.26(a) to prove that the posterior distribution
. Use Exercise 5.26(a) to prove that the posterior distribution  is the same as the (conditional) distribution of
is the same as the (conditional) distribution of  ,
,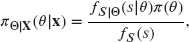
where
 is the pf of
is the pf of  and
and  is the marginal pf of S.
is the marginal pf of S. - 13.21 (*) The number of claims in one year, Y, has a Poisson distribution with parameter
 . The parameter
. The parameter  has a exponential distribution with pdf
has a exponential distribution with pdf  . A particular insured had no claims in one year. Determine the posterior distribution of
. A particular insured had no claims in one year. Determine the posterior distribution of  for this insured.
for this insured. - 13.22 (*) The number of claims in one year, Y, has a Poisson distribution with parameter
 . The prior distribution has a gamma distribution with pdf
. The prior distribution has a gamma distribution with pdf 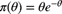 . There was one claim in one year. Determine the posterior pdf of
. There was one claim in one year. Determine the posterior pdf of  .
. - 13.23 (*) Each individual car's claim count has a Poisson distribution with parameter
 . All individual cars have the same parameter. The prior distribution is gamma with parameters
. All individual cars have the same parameter. The prior distribution is gamma with parameters  and
and  . In a two-year period, the insurer covers 750 and 1,100 cars in years 1 and 2, respectively. There were 65 and 112 claims in years 1 and 2, respectively. Determine the coefficient of variation of the posterior gamma distribution.
. In a two-year period, the insurer covers 750 and 1,100 cars in years 1 and 2, respectively. There were 65 and 112 claims in years 1 and 2, respectively. Determine the coefficient of variation of the posterior gamma distribution. - 13.24 (*) The number of claims, r, made by an individual in one year has a binomial distribution with pf
 . The prior distribution for
. The prior distribution for  has pdf
has pdf  . There was one claim in a one-year period. Determine the posterior pdf of
. There was one claim in a one-year period. Determine the posterior pdf of  .
. - 13.25 (*) The number of claims for an individual in one year has a Poisson distribution with parameter
 . The prior distribution for
. The prior distribution for  is exponential with an expected value of 2. There were three claims in the first year. Determine the posterior distribution of
is exponential with an expected value of 2. There were three claims in the first year. Determine the posterior distribution of 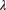 .
. - 13.26 (*) The number of claims in one year has a binomial distribution with
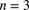 and
and  unknown. The prior distribution for
unknown. The prior distribution for  is beta with pdf
is beta with pdf  . Two claims were observed. Determine each of the following:
. Two claims were observed. Determine each of the following:
- The posterior distribution of
 .
. - The expected value of
 from the posterior distribution.
from the posterior distribution.
- The posterior distribution of
- 13.27 (*) The number of claims is binomial, with
 and q unknown. The prior distribution is
and q unknown. The prior distribution is  ,
,  . A single observation has a value of 2. Determine the mean and mode of the posterior distribution of q.
. A single observation has a value of 2. Determine the mean and mode of the posterior distribution of q.
13.4 Computational Issues
It should be obvious by now that all Bayesian analyses proceed by taking integrals or sums. So, at least conceptually, it is always possible to do a Bayesian analysis. However, only in rare cases are the integrals or sums easy to do, and that means most Bayesian analyses will require numerical integration. While one-dimensional integrations are easy to do to a high degree of accuracy, multidimensional integrals are much more difficult to approximate. A great deal of effort has been expended with regard to solving this problem. A number of ingenious methods have been developed. Some of them are summarized in Klugman [72]. However, the one that is widely used today is called Markov Chain Monte Carlo simulation. A good discussion of this method can be found in Gelman et al. [42].

