![]()
Numerical Series and Power Series
Numerical Series of Non-negative Terms
MATLAB enables you to work with numerical series of non-negative terms and with alternating series. In addition, the commands relating to limits allow you to work with different convergence tests for numerical series.
In the case where the sum is convergent, there are various functions available to help you to find the sum. We have the following:
|
symsum(S,v,a,b) |
Sums the series S as the variable v varies from a to b. syms x; symsum(x^k/sym('k!'), k, 0, inf) |
|
symsum(S,v) |
Sums the series S as the variable v varies from 0 to v-1. >> symsum(k^2,k) ans = k^3/3 - k^2/2 + k/6 |
|
r = symsum (S) |
Sums the series S as its symbolic variable k (as determined by findsym) ranges from 0 up to k-1. >> r=symsum(k^2) r = k^3/3 - k^2/2 + k/6 |
|
symsum (S, a, b) |
Sums the series S as its symbolic variable k (determined by findsym) ranges between a and b >> syms k n >> symsum(k,0,n-1) ans = (n*(n - 1))/2 |
Convergence Criteria: The Ratio Test
There are several criteria for determining whether a series of positive terms is convergent (i.e. has a finite sum). Among the most common are the ratio test or d'Alembert criterion, which read as follows:
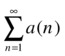 is convergent if
is convergent if 
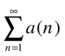 is divergent if
is divergent if 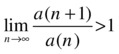
If the limit is 1, we cannot conclude anything about the convergence of the series.
As a first example, we analyze the convergence of the series  .
.
Using the ratio test we first calculate the limit 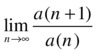 .
.
>> syms n
>> f='n/2^n'
f =
n/2^n
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1/2
As the limit is less than 1, the series is convergent. We can calculate the sum of its first k terms in the following way:
>> syms n k
>> symsum(n/2^n,0,k-1)
ans =
2 - (2*(k + 1))/2^k
If we want to find the infinite sum of the series we have:
>> symsum(n/2^n,0,inf)
ans =
2
Therefore we conclude that:
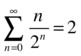
As a second example, we look at the convergence of the series 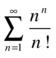 .
.
Using the ratio test we calculate 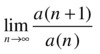 :
:
>> syms n
>> f=n^n/sym('n!')
f =
n^n/factorial(n)
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
exp(1)
As the limit is greater than 1, the series is divergent.
Raabe’s Criterion
Raabe’s criterion may be used to analyze the convergence of a series if the ratio test, or similar tests, fail. If the ratio test returns a value of 1, one can often use the criterion of Raabe or Duhamel, which reads as follows:
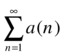 is convergent if
is convergent if 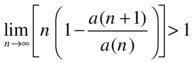
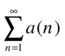 is divergent if
is divergent if 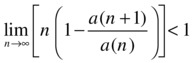
If the limit is 1, we cannot conclude anything about the convergence of the series.
As an example, we try to determine whether the series 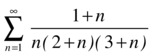 converges.
converges.
Obviously, we initially try to apply the ratio test:
>> syms n
>> f='(1+n)/(n*(2+n)*(3+n))'
f =
(1+n)/(n*(2+n)*(3+n))
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1
As the limit is 1, we cannot conclude anything about the convergence of the series. Instead, we try the Raabe criterion.
>> limit(n*(1-subs(f,n+1)/subs(f,n)),inf)
ans =
2
The limit is greater than 1, so we conclude that the series converges. We find its sum in the following way:
>> symsum((1+n)/(n*(2+n)*(3+n)),1,inf)
ans =
17/36
The Root Test
The Cauchy criterion or root test also improves on the ratio test and sometimes the Raabe criterion when analyzing the convergence of a series. The root test reads as follows:
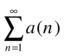 is convergent if
is convergent if ![]()
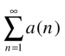 is divergent if
is divergent if ![]()
If the limit is 1, we cannot say anything about the convergence of the series.
As a first example, we try to determine whether the series 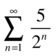 converges.
converges.
We use the root test in the following way:
>> syms n
>> limit((5/2^n)^(1/n),inf)
ans =
1/2
As the limit is less than 1, the series converges.
If we had applied the ratio and Raabe criteria we would have found:
>> f='5/2^n'
f =
5/2^n
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1/2
>> limit(n*(1-subs(f,n+1)/subs(f,n)),inf)
ans =
Inf
>> limit((5/2^n)^(1/n),inf)
ans =
1/2
So using either criteria, we would have concluded that the series converges (limit less than 1 for the ratio test and limit greater than 1 for the Raabe criterion).
The sum of the series is calculated by:
>> symsum(5/2^n,1,inf)
ans =
5
As a further example we analyze whether the following series converges:
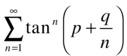
according to the values of the parameters p and q.
As its general term is an nth power, it is logical to try to use the root test. We have:
>> syms n p q
>> simplify(limit(tan(p+q/n),n,inf))
ans =
tan(p)
Then, for values of p (say, in the interval (0, Pi/2)) such that tan (p) < 1 the series converges. These values of p satisfy 0 < p < Pi/4. For values of p such that ran(p) > 1 the series diverges. These values of p satisfy Pi/4 < p < Pi/2. MATLAB does not offer the exact value or an approximate value for the sum of this series.
>> simplify(symsum(tan(p+q/n),n,1,inf))
ans =
sum(tan(p + q/n), n = 1..Inf)
Other Convergence Criteria
There are additional criteria one can use to study the convergence of series of positive terms.
The Gauss majorization criterion says that if a series of non-negative terms is dominated by a convergent series then it too is convergent (an is dominated by bn if an < bn for all n). In addition, if a series dominates a divergent series, then it is divergent.
The comparison test of the second kind ensures that if the limit of the ratio an /bn exists and is positive then the series ![]() and
and ![]() are either both convergent or both divergent.
are either both convergent or both divergent.
A third approach is given by the result that the two series 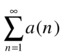 and
and 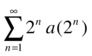 are either both convergent or both divergent.
are either both convergent or both divergent.
As a first example, we consider the following series:
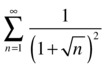
Initially we try to apply Raabe’s criterion and the ratio test:
>> f='1/(1+n^(1/2))^2'
f =
1/(1+n^(1/2))^2
>> limit(n*(1-subs(f,n+1)/subs(f,n)),inf)
ans =
1
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1
In both cases the limit is 1. So at the moment we cannot conclude anything about the convergence of the series.
We now apply the comparison test of the second kind to compare our series with the divergent harmonic series with general term 1/n:
>> limit(subs(f,n)/(1/n),inf)
ans =
1
As the limit is greater than zero, we conclude that the initial series is also divergent.
We reach the same conclusion by applying the root test.
>> limit(subs(f, n)^1/n, inf)
ans =
0
Since the limit is less than 1, the series diverges.
As a second example, consider the following series:
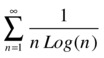
We apply the criterion that ensures that the series 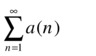 and
and 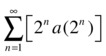 have the same character of convergence.
have the same character of convergence.
>> f ='1 / (n * log (n))'
f =
1 / (n * log (n))
>> 2 ^ n * subs(f,2^n)
ans =
1/log(2^n)
Thus our series has the same character of convergence as the series with general term 1/(nlog(2)), and since
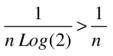
we see that the series with general term 1/(nlog(2)) diverges. We conclude that the original series also diverges.
Alternating Numerical Series. Dirichlet and Abel’s Criteria
So far we have only considered numerical series of positive terms. From now on we will consider numerical series that have alternating positive and negative terms. Usually these series are called alternating series.
In the case of alternating series, the concept of absolute convergence is fundamental. A series ∑a(n) is said to be absolutely convergent if the series of moduli ∑ |a (n) | is convergent. As the series of moduli is a series of positive terms, we already know how to analyze it. If a series is absolutely convergent then it is convergent, but not conversely.
There are two classical criteria that can be used to analyze the convergence of alternating series, which will allow us to resolve most problems involving alternating series.
Dirichlet’s criterion says that if the sequence of partial sums of ∑a(n) is bounded and {b(n)} is a decreasing sequence that has limit 0, then the series ∑a(n)b(n) is convergent.
Abel’s criterion says that if ∑a(n) is convergent and {b(n)} is a monotone convergent sequence, then the series ∑a(n)b(n) is convergent.
As a first example, we consider the alternating series:
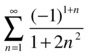
To analyze the convergence of the series, we study whether or not it is absolutely convergent, i.e. if the following series of positive terms is convergent:
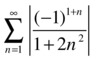
We apply to this series of positive terms the comparison test of the second kind, comparing with the convergent series with general term 1/n2
>> f ='abs((-1)^(1+n)/(1+2*n^2))'
f =
abs((-1)^(1+n)/(1+2*n^2))
>> limit(subs(f,n)/(1/n^2), inf)
ans =
1/2
As the limit is greater than zero, the series of positive terms considered is convergent, and so the initial series is absolutely convergent and, therefore, convergent.
As a second example we consider the series:
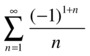
If we put ![]() and
and 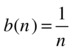 , we have that Σa(n) has bounded partial sums and {b(n)} is monotone decreasing with limit 0.
, we have that Σa(n) has bounded partial sums and {b(n)} is monotone decreasing with limit 0.
Using Dirichlet’s criterion we conclude that the considered alternating series is convergent.
Power Series
A power series has the following structure:
![]()
The main objective is to calculate the range of convergence of the series, i.e., the range of values of x for which the corresponding numerical series is absolutely convergent.
If the variable x is replaced by a numerical value, the power series becomes a numerical series. The criteria used to determine whether the series converges are those already used for numerical series. Since we are considering the absolute convergence of the series, we are considering series of positive terms, so the commonly used criteria are the root and ratio tests.
As a first example, we calculate the interval of convergence for the following power series:
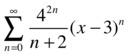
Via the ratio test we will try to calculate the values of x for which the given series is convergent.
>> f ='(4^(2*n)) * ((x-3)^n) / (n + 2)'
f =
(4 ^(2*n)) * ((x-3) ^ n) / (n + 2)
>> limit(simplify(subs(f,n,n+1)/subs(f,n,n)), n, inf)
ans =
16 * x - 48
The series will be convergent when |16x - 48| <1. To find the extreme values of the interval of convergence we solve the following equations:
>> [solve('16*x-48=1'), solve('16*x-48=-1')]
ans =
[49/16, 47/16]
Thus, the condition |16x - 48| <1 is equivalent to the following:
47/16 < x < 49/16
We already know that in this interval the series is convergent. Now we need to analyze the behavior of the series at the end points of the interval. First we consider x = 49/16.
>> g1=simplify(subs(f,x,49/16))
G1 =
1 /(n + 2)
We have to analyze the numerical series of positive terms  .
.
Note that the ratio test and Raabe’s criterion return a limit of 1, so we must use an alternative approach.
>> limit(simplify(subs(g1,n+1)/subs(g1,n)), n, inf)
ans =
1
>> limit(n*(1-subs(g1,n+1)/subs(g1,n)),inf)
ans =
1
We will apply the comparison test of the second kind, comparing the series of the problem with the divergent harmonic series with general term 1 /n:
>> limit(subs(g1,n)/(1/n),inf)
ans =
1
As the limit is greater than zero, the series is divergent.
We now analyze the endpoint x =47/16:
>> g2=simplify(subs(f,x,47/16))
g2 =
(-1)^n/(n + 2)
We have to analyze the alternating series 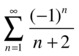 .
.
By Dirichlet’s criterion, since the series with general term (- 1)n has bounded partial sums, and the sequence with general term 1 / (n + 2) is decreasing toward 0, the alternating series converges. The interval of convergence of the power series is therefore the half-open interval [47/16, 49/16).
Power Series Expansions
MATLAB includes commands that allow you to address the problem of the local approximation of a real function of a real variable at a point by replacing the initial function by a simple equivalent. The most common way to do this is to replace an arbitrary function f(x) by a power series P(x) so that the values of f(x) and P(x) are close in the neighborhood of the given point. This power series is called a power series expansion of the function.
The MATLAB commands used to work with power series are presented in the following table:
|
taylor (f) |
Returns the MacLaurin series of f up to degree 5. >> syms x f = exp(x^2); >> pretty(taylor(f)) 4 x 2 -- + x + 1 2 |
|
taylor (f, n) |
Returns the MacLaurin series of f up to degree n, where n is a natural number. >> pretty(taylor(f,7)) 6 4 x x 2 -- + -- + x + 1 6 2 |
|
taylor(f, a) |
Returns the Taylor series of f in a neighborhood of the real number a up to degree 5. If a is a natural number it is necessary to use the function taylor(f, 5, a). >> pretty(simplify(taylor(f,1/2))) / 1 5 4 3 2 exp| - | (2592 x - 2480 x + 2960 x + 1800 x + 250 x + 2969) 4 /` --------------------------------------------------------------- 3840 |
|
taylor(f, n, v) |
Finds the MacLaurin series of f up to degree n-1 in the variable v. >> pretty(taylor(f,3,p)) 2 2 2 2 2 exp(p) + exp(p) (2 p + 1) (p - x) - 2 p exp(p) (p - x) |
|
taylor(f, n, v, a) |
Finds the Taylor series of f in a neighborhood of the real number a up to degree n-1 in the variable v. >> pretty(taylor(f,3,p,2)) 2 exp(4) + 4 exp(4) (x - 2) + 9 exp(4) (x - 2) |
As a first example we calculate the Taylor polynomial of sinh(x) at the point x = 0 (the MacLaurin series) up to degree 13.
>> syms x
>> f=sinh(x)
f =
sinh(x)
>> taylor(f,13)
ans =
x^11/39916800 + x^9/362880 + x^7/5040 + x^5/120 + x^3/6 + x
As a second example we calculate the Taylor expansion of 1/(1+x) at the point x = 2 up to degree 6.
>> syms x
>> f=1/(1+x)
f =
1/(x + 1)
>> pretty(taylor(f,6,2))
2 3 4 5
(x - 2) x (x - 2) (x - 2) (x - 2) 5
-------- - - - -------- + -------- - -------- + -
27 9 81 243 729 9
EXERCISE 6-1
Study the convergence and, if possible, find the sum of the following series:
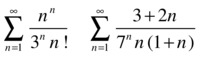
We apply the ratio test for the first series:
>> syms n
>> f=n^n/(sym('n!')*(3^n))
f =
n^n/(3^n*factorial(n))
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
exp(1)/3
The limit is less than 1, so the series turns out to be convergent. Therefore, we can try to calculate its sum as follows:
>> vpa(simplify(symsum(f,1,inf)))
ans =
1.6250941822939141659377675737628
Now we apply the ratio test for the second series:
>> f=(2*n+3)/(n*(n+1)*(7^n))
f =
(2*n + 3)/(7^n*n*(n + 1))
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1/7
As the limit is less than 1, the series is convergent. MATLAB will attempt to return the exact sum, but it may be in a complicated form, in terms of special functions. Here we approximate the sum, as before:
>> vpa(symsum(f,1,inf))
ans =
0.38339728069096678282849845975009
EXERCISE 6-2
Study the convergence and, if possible, find the sum of the following series:
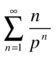 ,
, 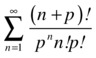
p = real parameter
We apply the ratio test for the first series:
>> syms n;
>> p=sym('p','real'),
>> f=n/p^n
f =
n/p^n
>> limit(subs(f,{n},{n+1})/subs(f,{n},{n}),n,inf)
ans =
1/p
Thus, if p > 1, the series converges, and if p < 1, the series diverges. If p = 1, we get the series with general term n, which diverges. When p is greater than 1, we find the sum of the series:
>> vpa(symsum(f,1,inf))
ans =
piecewise([1.0 < Re(n), n*zeta(n)])
We will apply the ratio test to the second series:
>> f=sym('(n+p)!')/(sym('p!')*(sym('n!')*(p^n)))
f =
factorial(n + p)/(p^n*factorial(n)*factorial(p))
>> vpa(simplify(limit(subs(f,{n},{n+1})/subs(f,{n},{n}),n,inf)))
ans =
1/p
Thus, if p > 1, the series converges, and if p < 1, the series diverges, and if p = 1, we get the series with general term n, which diverges. When p is greater than 1, we try to find the sum of the series:
>> vpa(simplify(symsum(f,1,inf)))
ans =
numeric::sum(factorial(n + p)/(p^(1.0*n)*factorial(p)),
p = 1..Inf)/factorial(n)
We see that MATLAB has been unable to find the sum.
Thus, if p > 1 the two series converge and if p < 1 the two series diverge. We have only been able to find the sum of the first series.
EXERCISE 6-3
Study the convergence and, if possible, find the sum of the following series:
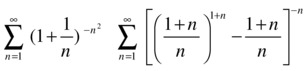
For the first series we apply the ratio test:
>> syms n
>> f =(1+1/n)^(-n^2)
f =
1/(1/n + 1)^(n^2)
>> limit(subs(f,n+1)/subs(f, n), inf)
ans =
1/exp (1)
As the limit is less than 1, the series converges. MATLAB can sum this series as follows:
>> vpa(symsum(f,1,inf))
ans =
0.81741943329783346091309999437311
We will apply the ratio test to the second series:
>> f = (((n + 1) / n) ^ (n + 1) - a (n + 1) /n) ^(-n)
f =
1 / (((n + 1)/n) ^(n + 1) - (n + 1) / n) ^ n
>> limit (subs(f,n+1) /subs (f, n), inf)
ans =
1 / (exp(1) - 1)
As the limit is less than 1, the series converges. The sum can be found with MATLAB as follows:
>> vpa(symsum(f,1,inf))
ans =
1.1745855750875866746226188496682
EXERCISE 6-4
Study the convergence and, if possible, find the sum of the following series:
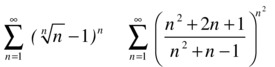
As the general term of both series is raised to a power of n, the root test may be applicable.
We apply the root test to the first series:
>> f = (n ^ (1/n) - 1) ^ n
f =
(n ^ (1/n) - 1) ^ n
>> limit(subs(f, n)^(1/n), inf)
ans =
0
As the limit is less than 1, the series is convergent. The sum is calculated as follows:
>> vpa(symsum(f,1,inf))
ans =
0.29759749220552960849982457076294
Now we apply the root test to the second series:
>> syms n
>> f = ((n^2+2*n+1) /(n^2+n-1))^(n^2)
f =
((n^2 + 2*n + 1) /(n^2 + n-1)) ^(n^2)
>> limit(subs(f,n)^(1/n),inf)
ans =
exp(1)
As the limit is greater than 1, the series diverges.
EXERCISE 6-5
Study the convergence and, if possible, find the sum of the following series:
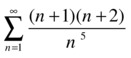
We try to apply the root, quotient, and Raabe criteria:
>> f=(n+1)*(n+2)/n^5
f =
((n + 1)*(n + 2))/n^5
>> limit(subs(f,n)^(1/n),inf)
ans =
1
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1
>> limit(n*(1-subs(f,n+1)/subs(f,n)),inf)
ans =
3
The root and ratio tests tell us nothing, but the Raabe criterion already assures us that the series converges (the limit is greater than 1). We find the sum.
>> vpa(symsum(f,1,inf))
ans =
6.522882114579748712610480224049
We can also analyze the series directly by using the comparison test of the second kind, comparing our series with the convergent series with general term 1/n3:
>> limit(f/(1/(n^3)),inf)
ans =
1
As the limit is greater than 0, the series is convergent.
EXERCISE 6-6
Study the convergence and, if possible, find the sum of the following series:
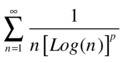 p = parameter > 0
p = parameter > 0
We apply the criterion that ensures that the series 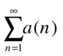 and
and 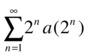 have the same character of convergence.
have the same character of convergence.
>> f=1/(n*(log(n))^p)
f =
1/(n*log(n)^p)
>> pretty((2^n)*subs(f,{n},{2^n}))
1
--------
n p
log(2 )
When p < 1, this series dominates the divergent series with general term n-p = 1/np. Thus the initial series also diverges.
When p > 1, this series is dominated by the convergent series with general term n-p = 1/np. Thus the initial series converges.
When p = 1, the series reduces to the series:
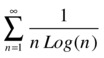
which can be tested by the same criteria as the previous one.
>> f=1/(n*(log(n)))
f =
1/(n*log(n))
>> pretty((2^n)*subs(f,{n},{2^n}))
1
-------
n
log(2 )
As this series dominates the divergent harmonic series with general term 1/n, it diverges. Therefore the initial series also diverges.
EXERCISE 6-7
Study the convergence of the following series:
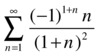
If we define ![]() and
and 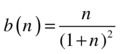 we have that a(n) has bounded partial sums and {b(n)} is monotone decreasing with limit 0.
we have that a(n) has bounded partial sums and {b(n)} is monotone decreasing with limit 0.
Using Dirichlet’s criterion we conclude that the considered alternating series is convergent.
Alternatively, we could have considered the absolute convergence of the series. In this case we observe that the ratio and root tests, and Raabe’s criterion, all give a limit of 1, so we cannot solve the problem.
>> f=n/(1+n)^2
f =
n/(n + 1)^2
>> limit(n*(1-subs(f,n+1)/subs(f,n)),inf)
ans =
1
>> limit(subs(f,n+1)/subs(f,n),inf)
ans =
1
>> limit(subs(f,n)^(1/n),inf)
ans =
1
Applying the comparison test of the second kind to this series of positive terms, comparing with the convergent series with general term 1/n2, we find:
>> limit(subs(f,n)/(1/n^2),inf)
ans =
Inf
As the limit is greater than zero, the series of positive terms considered is convergent, and so the initial series is absolutely convergent and, therefore, convergent. We now calculate its sum.
>> f=((-1)^n)*(n/(n + 1)^2)
f =
((-1)^n*n)/(n + 1)^2
>> vpa(symsum(f,1,inf))
ans =
-0.12931985286416790881897546186484
EXERCISE 6-8
Study the interval of convergence of the following power series:
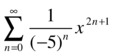
We apply the root test:
>> syms x n
>> f=x^(2*n+1)/(-5)^n
f =
x^(2*n + 1)/(-5)^n
>> limit(subs(f,{n},{n+1})/subs(f,{n},{n}),n,inf)
ans =
-x^2/5
The series is absolutely convergent when |-x ^ 2/5| < 1.
The condition |-x ^ 2/5| < 1 is equivalent to -sqrt(5) < x < sqrt(5). Thus, we have determined the possible intervals of convergence of the power series. We will now analyze the endpoints:
>> pretty(simplify(subs(f,{x},{sqrt(5)})))
1/2
5
-----
n
(-1)
>> pretty(simplify(subs(f,{x},{-sqrt(5)})))
n 1/2
- (-1) 5
Both series are obviously divergent alternating series. Therefore, the interval of convergence of the given power series is: –sqrt(5) < x < sqrt(5).
EXERCISE 6-9
Calculate the MacLaurin series of Ln(x + 1) up to degree 5. Also find the MacLaurin series up to degree 8.
>> syms x
>> f=log(x+1)
f =
log(x + 1)
>> pretty(taylor(f))
5 4 3 2
x x x x
-- - -- + -- - -- + x
5 4 3 2
>> pretty(taylor(f,8))
7 6 5 4 3 2
x x x x x x
-- - -- + -- - -- + -- - -- + x
7 6 5 4 3 2
EXERCISE 6-10
Calculate the Taylor series of 1/(2-x ) at the point x = 1 up to degree 7. Also find the Taylor series of sin(x ) at the point x = 2 up to degree 8.
>> syms x
>> f = 1 /(2-x)
f =
-1 /(x-2)
>> pretty(taylor(f,7,1))
2 3 4 5 6
x + (x - 1) + (x - 1) + (x - 1) + (x - 1) + (x - 1)
>> f=sin(x);
>> pretty(taylor(f,8,pi))
3 5 7
(pi - x) (pi - x) (pi - x)
pi - x - --------- + --------- - ---------
6 120 5040
Both series show that the term which would correspond to the greatest degree is void.
