Q: One application of geometric algorithms mentioned at the start of this chapter was determining whether the track of an object transgresses a restricted region. If we assume that the track we follow begins outside of the restricted region, a simple approach to this problem is to determine whether any line segment in the track intersects with any line segment defining the restricted region. What is the running time of this approach if we use the lint operation presented in this chapter?

A: The runtime complexity of this approach is O (nm), where n is the number of line segments in the track and m is the number of line segments defining the restricted region. This is because for each of the n line segments in the track, we call lint once for each of the m line segments in the restricted region. Since lint runs in a constant amount of time, the runtime complexity of the solution overall is O (nm).

Q: Determining the orientation of two points with respect to a third is an important part of the algorithms presented for determining whether line segments intersect and computing convex hulls. Formally, given points p ₁ , p ₂, and p ₃, we determine the orientation of p ₃ relative to p ₂ with respect to p ₁ by treating the line segments from p ₁ to p ₂ and p ₁ to p ₃ as vectors U and V. We then use the sign of the z-component of the cross product U × V as a gauge of orientation. What is the orientation of the points if we compute the cross product V × U? In other words, given a specific orientation of p ₃ relative to p ₂, what is the orientation of p ₂ relative to p ₃?

A: The answer to this question is a matter of perspective. Imagine two people facing forward in a room with a door behind them. Unless the two individuals line up perfectly with the door (one in front of the other), person A will see person B to his left, whereas person B will see person A to his right, and vice versa. The neat thing about cross products is that they reflect this perspective mathematically. When we compute the orientation of p ₃ relative to p ₂ with respect to p ₁, we get an indication of where p ₃ is from the perspective of p ₂. For example, p ₃ may be clockwise from p ₂. When we compute the orientation of p ₂ relative to p ₃, we get an indication of where p ₂ is from the perspective of p ₃. These perspectives are always equal but opposite to one another (except in the boundary case when p ₂ and p ₃ form a straight line with p ₁). That is, U × V is always equal to but of opposite sign as V × U (if p ₂ and p ₃ form a straight line with p ₁, U × V and V × U are both 0, and the line segments from p ₁ to p ₂ and p ₁ to p ₃ are collinear). The formula given earlier in the chapter for z ₁ when testing for intersecting line segments comes from U × V. To compute V × U, we exchange the positions of x ₂ and x ₃ and of y ₂ and y ₃ in the formula. This yields an equivalent result but with the sign reversed. Therefore, if p ₃ is clockwise from p ₂, for example, this tells us that p ₂ is counterclockwise from p ₃, as we would expect.

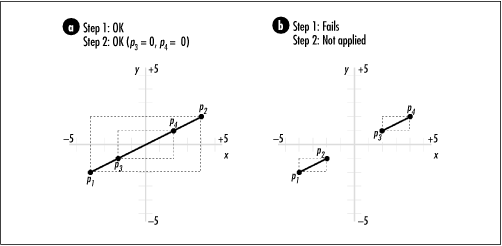
Q: To test whether two line segments from points p ₁ to p ₂ and p ₃ to p ₄ intersect, we first examine whether the bounding boxes of the line segments intersect and then compare the orientation of p ₃ relative to p ₂ with that of p ₄ relative to p ₂. In what situation do the bounding boxes intersect when the orientations of both p ₃ and p ₄ are 0? Is it possible to have bounding boxes that do not intersect when the orientations of p ₃ and p ₄ are both 0?

A: Recall that when the orientation of either p ₃ or p ₄ is 0, it means that the line segment from either p ₁ to p ₃ or p ₁ to p ₄ is collinear with the line segment from p ₁ to p ₂. If the bounding boxes of the two line segments intersect as well, this tells us that at least some parts of the segments overlay each other (see Figure 17.9a). Therefore, the line segments intersect. On the other hand, it is possible to have two line segments that are collinear without intersecting. This occurs when the segments would overlay each other if either were long enough, but neither has the length necessary to do so (see Figure 17.9b).

Figure 17.9. Collinear line segments whose bounding boxes (a) intersect and (b) do not intersect

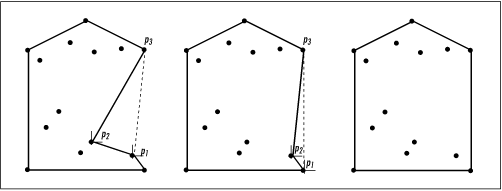
Q: In this chapter we learned that the smallest polygon surrounding a set of points is called a convex hull. This name implies that the polygon is always convex. Why is this?

A: Recall that a polygon is convex if any line segment connecting two points inside the polygon lies completely inside the polygon itself; otherwise, the polygon is concave. To understand why a convex hull is always convex, consider a concave polygon that surrounds a set of points. For any sequence of three points p ₁, p ₂, and p ₃ defining a concave region, if we replace the edges from p ₁ to p ₂ and p ₂ to p ₃ with a single edge from p ₁ to p ₃, we can reduce the size of the polygon while keeping p ₂ enclosed. We know that the size of the polygon will be reduced because it is always shorter to go from one point to another than through a third point first. We know that p ₂ will still be enclosed by the resulting polygon because the angle from p ₂ to p ₃ is less than the angle from p ₁ to p ₂. Therefore, since a convex polygon will always be shorter than any concave one that encloses the same points, a convex hull must be convex (see Figure 17.10).

Figure 17.10. Showing that the smallest polygon enclosing a set of points is always convex

Q: Suppose in the approximation for distances on Earth presented in this chapter we would like to improve the method used in the function geodist. Specifically, we would like to do something to take into account the change in the Earth’s radius at different latitudes and longitudes. How can we do this?

A: One way to make this improvement is to use the fact that both points passed into geodist have their own value for the spherical coordinate ρ. When we treat the Earth as a perfect sphere, we set the rho member of each point to the same value since we are considering the distance from the Earth’s center to the surface to be the same everywhere. However, a better approach would be to set rho for each point to the actual distance from the center of the Earth to the point and then compute an average of the two rho members for the radius of the arc. Although this does not perfect the distance computation, it does generally improve it.