The covariance matrix Σ is real and symmetric. If we apply the eigendecomposition, we get (for our purposes it's more useful to keep V^-1 instead of the simplified version V^T):

V is an orthogonal matrix (thanks to the fact that Σ is symmetric) containing the eigenvectors of Σ (as columns), while Ω is a diagonal matrix containing the eigenvalues. Let's suppose we sort both eigenvalues (λ₁, λ₂, ..., λ_m) and the corresponding eigenvectors (v₁, v₂, ..., v_m) so that:

Moreover, let's suppose that λ₁ is dominant over all the other eigenvalues (it's enough that λ₁ > λ_i with i ≠ 1). As the eigenvectors are orthogonal, they constitute a basis and it's possible to express the vector w, with a linear combination of the eigenvectors:

The vector u contains the coordinates in the new basis. Let's now consider the modification to the covariance rule:

If we apply the rule iteratively, we get a matrix polynomial:

Exploiting the Binomial theorem and considering that Σ⁰=I, we can get a general expression for w^(k) as a function of w⁽⁰⁾:

Let's now rewrite the previous formula using the change of basis:

The vector u⁽⁰⁾ contains the coordinates of w⁽⁰⁾ in the new basis; hence, w^(k) is expressed as a polynomial where the generic term is proportional to VΩⁱu⁽⁰⁾.

Let's now consider the diagonal matrix Ω^k:

The last step derives from the hypothesis that λ₁ is greater than any other eigenvalue and when k → ∞, all λ_i≠1^k << λ₁^k. Of course, if λ_i≠1 > 1, λ_i≠1^k will grow as well as λ₁^k however, the contribution of the secondary eigenvalues to w^(k) becomes significantly weaker when k → ∞. Just to understand the validity of this approximation, let's consider the following situation where λ₁ is slightly larger that λ₂:

The result shows a very important property: not only is the approximation correct, but as we're going to show, if an eigenvalue λ_i is larger than all the other ones, the covariance rule will always converge to the corresponding eigenvector v_i. No other stable fixed points exist! 

This hypothesis is no more valid if λ₁ = λ₂ = ... = λ_n. In this case, the total variance is explained equally by the direction of each eigenvector (a condition that implies a symmetry which isn't very common in real-life scenarios). This situation can also happen when working with finite-precision arithmetic, but in general, if the difference between the largest eigenvalue and the second one is less than the maximum achievable precision (for example, 32-bit floating point), it's plausible to accept the equality.

Of course, we assume that the dataset is not whitened, because our goal (also in the next paragraphs) is to reduce the original dimensionality considering only a subset of components with the highest total variability (the decorrelation, like in Principal Component Analysis (PCA), must be an outcome of the algorithm, not a precondition). On the other side, zero-centering the dataset could be useful, even if not really necessary for this kind of algorithm.

If we rewrite the expression for w_k considering this approximation, we obtain the following:

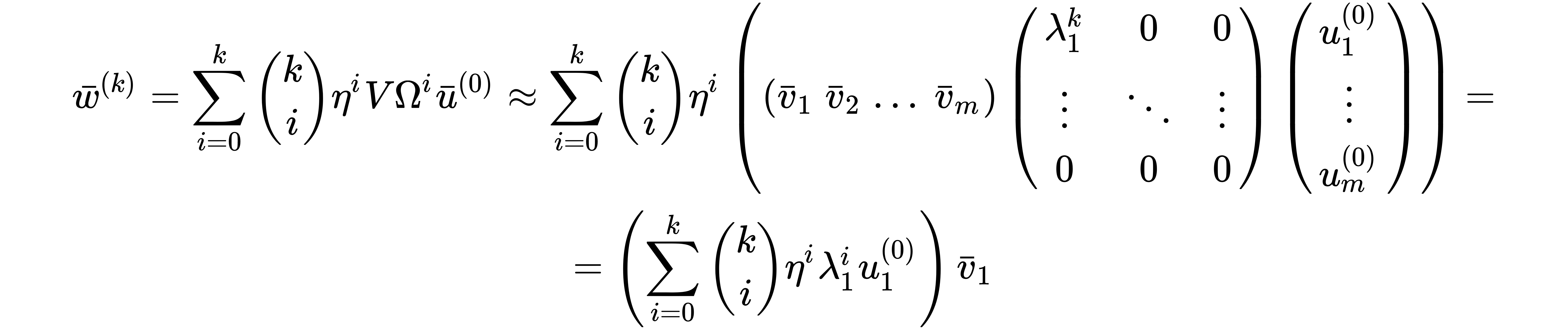
As a₁v + a₂v + ... + a_kv ∝ v, this result shows that, when k → ∞, w_k will become proportional to the first eigenvector of the covariance matrix Σ (if u₁⁽⁰⁾ is not null) and its magnitude, without normalization, will grow indefinitely. The spurious effect due to the other eigenvalues becomes negligible (above all, if w is divided by its norm, so that the length is always ||w|| = 1) after a limited number of iterations.

However, before drawing our conclusions, an important condition must be added:

In fact, if w(0) were orthogonal to v1, we would get (the eigenvectors are orthogonal to each other):

This important result shows how a Hebbian neuron working with the covariance rule is able to perform a PCA limited to the first component without the need for eigendecomposing Σ. In fact, the vector w (we're not considering the problem of the increasing magnitude, which can be easily managed) will rapidly converge to the orientation where the input dataset X has the highest variance. In Chapter 5, EM Algorithm and Applications, we discussed the details of PCA; in the next paragraph, we're going to discuss a couple of methods to find the first N principal components using a variant of the Hebb's rule.