Self-organizing maps (SOMs) have been proposed by Willshaw and Von Der Malsburg (Willshaw D. J., Von Der Malsburg C., How patterned neural connections can be set up by self-organization, Proceedings of the Royal Society of London, B/194, N. 1117) to model different neurobiological phenomena observed in animals. In particular, they discovered that some areas of the brain develop structures with different areas, each of them with a high sensitivity for a specific input pattern. The process behind such a behavior is quite different from what we have discussed up until now, because it's based on competition among neural units based on a principle called winner-takes-all. During the training period, all the units are excited with the same signal, but only one will produce the highest response. This unit is automatically candidate to become the receptive basin for that specific pattern. The particular model we are going to present has been introduced by Kohonen (in the paper Kohonen T., Self-organized formation of topologically correct feature maps, Biological Cybernetics, 43/1) and it's named after him.

The main idea is to implement a gradual winner-takes-all paradigm, to avoid the premature convergence of a neuron (as a definitive winner) and increment the level of plasticity of the network. This concept is expressed graphically in the following graph (where we are considering a linear sequence of neurons):

In this case, the same pattern is presented to all the neurons. At the beginning of the training process (t=0), a positive response is observed in x_i-2 to x_i+2 with a peak in x_i. The potential winner is obviously x_i, but all these units are potentiated according to their distance from x_i. In other words, the network (which is trained sequentially) is still receptive to change if other patterns produce a stronger activation. If instead x_i keeps on being the winner, the radius is slightly reduced, until the only potentiated unit will be x_i. Considering the shape of this function, this dynamic is often called Mexican Hat. With this approach, the network remains plastic until all the patterns have been repeatedly presented. If, for example, another pattern elicits a stronger response in x_i, it's important that its activation is still not too high, to allow a fast reconfiguration of the network. At the same time, the new winner will probably be a neighbor of x_i, which has received a partial potentiation and can easily take the place of x_i.

A Kohonen SOM (also known as Kohonen network or simply Kohonen map) is normally represented as a bidimensional map (for example, a square matrix m × m, or any other rectangular shape), but 3D surfaces, such as spheres or toruses are also possible (the only necessary condition is the existence of a suitable metric). In our case, we always refer to a square matrix where each cell is a receptive neuron characterized by a synaptic weight w with the dimensionality of the input patterns:

During both training and working phases, the winning unit is determined according to a similarity measure between a sample and each weight vector. The most common metric is the Euclidean; hence, if we consider a bidimensional map W with a shape (k × p) so that W ∈ ℜ^{k × p × n}, the winning unit (in terms of its coordinates) is computed as follows:

As explained before, it's important to avoid the premature convergence because the complete final configuration could be quite different from the initial one. Therefore, the training process is normally subdivided into two different stages. During the first one, whose duration is normally about 10-20% of the total number of iterations (let's call this value t_max), the correction is applied to the winning unit and its neighbors (computed by adopting a decaying radius). Instead, during the second one, the radius is set to 1.0 and the correction is applied only to the winning unit. In this way, it's possible to analyze a larger number of possible configurations, automatically selecting the one associated with the least error. The neighborhood can have different shapes; it can be square (in closed 3D maps, the boundaries don't exist anymore), or, more easily, it's possible to employ a radial basis function based on an exponentially decaying distance-weight:

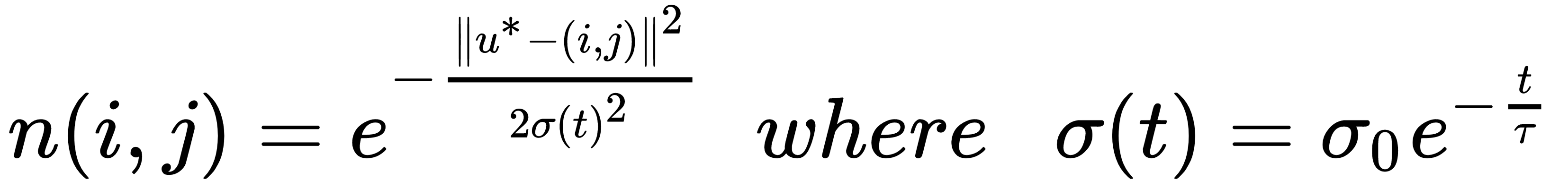
The relative weight of each neuron is determined by the σ(t). σ₀ function is the initial radius and τ is a time-constant that must be considered as a hyperparameter which determines the slope of the decaying weight. Suitable values are 5-10% of the total number of iterations. Adopting a radial basis function, it's not necessary to compute an actual neighborhood because the multiplication factor n(i, j) becomes close to zero outside of the boundaries. A drawback is related to the computational cost, which is higher than a square neighborhood (as the function must be computed for the whole map); however, it's possible to speed up the process by precomputing all the squared distances (the numerator) and exploiting the vectorization features offered by packages such as NumPy (a single exponential is computed every time).

The update rule is very simple and it's based on the idea to move the winning unit synaptic weights closer to the pattern, x_i, (repeated for the whole dataset, X):

The η(t) function is the learning rate, which can be fixed, but it's preferable to start with a higher value, η₀ and let it decay to a target final value, η_∞:

In this way, the initial changes force the weights to align with the input patterns, while all the subsequent updates allow slight modifications to improve the overall accuracy. Therefore, each update is proportional to the learning rate, the neighborhood weighted distance, and the difference between each pattern and the synaptic vector. Theoretically, if Δw_ij is equal to 0.0 for the winning unit, it means that a neuron has become the attractor of a specific input pattern, and its neighbors will be receptive to noisy/altered versions. The most interesting aspect is that the complete final map will contain the attractors for all patterns which are organized to maximize the similarity between adjacent units. In this way, when a new pattern is presented, the area of neurons that maps the most similar shapes will show a higher response. For example, if the patterns are made up of handwritten digits, attractors for the digit 1 and for digit 7 will be closer than the attractor, for example, for digit 8. A malformed 1 (which could be interpreted as 7) will elicit a response that is between the first two attractors, allowing us to assign a relative probability based on the distance. As we're going to see in the example, this feature yields to a smooth transition between different variants of the same pattern class avoiding rigid boundaries that oblige a binary decision (like in a K-means clustering or in a hard classifier). 

The complete Kohonen SOM algorithm is as follows:

1. Randomly initialize W⁽⁰⁾. The shape is (k × p × n).
2. Initialize nb_iterations, the total number of iterations, and t_max (for example, nb_iterations = 1000 and t_max = 150).
3. Initialize τ (for example, τ = 100).
4. Initialize η₀ and η_∞ (for example, η₀ = 1.0 and η_∞ = 0.05).
5. For t = 0 to nb_iterations:
   
   1. If t < t_max:
      1. Compute η(t)
      2. Compute σ(t)
   2. Otherwise:
      1. Set η(t) = η_∞
      2. Set σ(t) = σ_∞
   3. For each x_i in X:
      1. Compute the winning unit u^* (let's assume that the coordinates are i, j)
      2. Compute n(i, j)
      3. Apply the weight correction Δw_ij^(t) to all synaptic weights W^(t)
   4. Renormalize W^(t) = W^(t) / ||W^(t)||^(columns) (the norm must be computed column-wise)