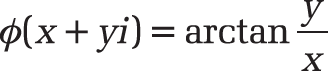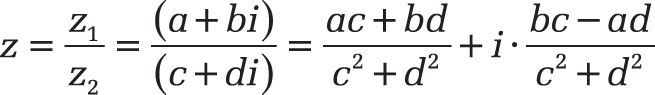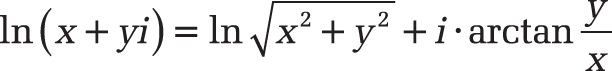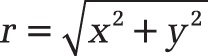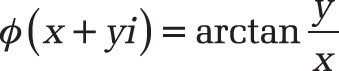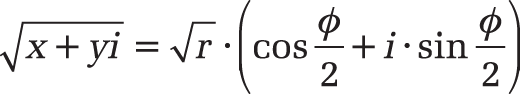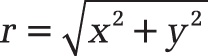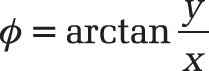There are 18 functions total for complex numbers. At this point, this chapter gives you some basic explanations. The individual functions will refer to this passage.
In school, you learned that any number squared is positive:
22 = 4
(–2)2 = 4
This also means that it is not possible to take the square root of negative numbers:
In the four basic arithmetic calculations, there is an inversion for every operation: addition ↔ subtraction and multiplication ↔ division. Shouldn’t this be applicable to exponentiation ↔ extracting a root? Mathematicians could not stop thinking about this problem. They regarded the call for “completeness of mathematics” as a given. This means that at least theoretically it should be possible to solve each and every mathematical problem—and they did find a solution in this case as well. It turned out that the solution was even significant in practice. Many technical calculations are based on it.
To solve these kinds of problems, you must leave the number line of real numbers (our everyday numbers, which go from –∞ through 0 to +∞) and enter the number planes above and below the number line.
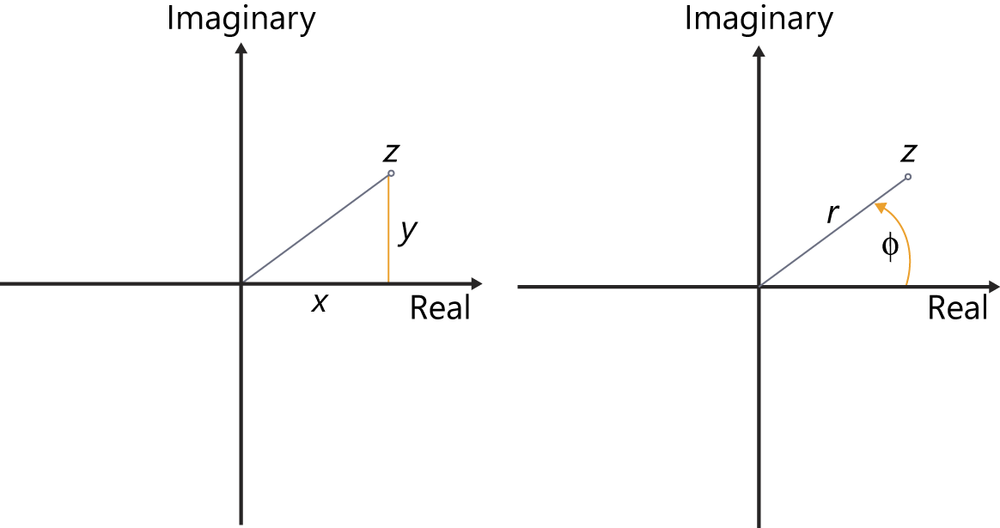
Similar to a two-dimensional coordinate system with an x-axis and a y-axis, complex numbers have a Cartesian coordinate system with an abscissa (x-axis) and an ordinate (y-axis). The number line of real numbers is the abscissa. The ordinate is called the imaginary unit i (or sometimes j). It has a property that incorporates the mathematical problems mentioned earlier. The y-axis is now called “imaginary” and the x-axis “real.” The numbers that can be represented in this coordinate system (the Argand plane) are called complex numbers.
Therefore, a complex number z is displayed like this:
z = x + yi
This is the algebraic form, with x as the real part (a line segment on the x-axis) and y as the imaginary part (a line segment on the y-axis) of the complex number (see Figure 17-6). The set of all numbers x + yi represents the body of complex numbers, each of which corresponds to an ordered pair (x;y). Not only can complex numbers be displayed in arithmetic format, they can also be described with polar coordinates with the value r and the angle Φ (the trigonometric form):
z = r(cosΦ + isinΦ)
The Excel functions IMARGUMENT() in IMARGUMENT(), IMCOS() in IMCONJUGATE(), and IMSIN() in IMSIN() belong to this notation.
Figure 17-6. Graphical display of a complex number in Cartesian representation and in polar representation.
The complex numbers are the basis for the function theory, in which, among many others, the Bessel functions were developed (see the section titled Background for BESSELJ() and others, from Background to ERF.PRECISE()/ERF()).
Important
The special treatment of complex numbers within a spreadsheet program such as Excel is the result of this fact: Complex numbers consist of two numbers, the real part and the imaginary part (or the value and the angle). Table calculations work with cells into which only one value can be entered in each: a text entry, a date/time, an error value, a logical value, a formula, or a number. To avoid this dilemma, in Excel, complex numbers are displayed as text, which concatenates both numbers and can appear in one single cell (similar to other “impossible numbers,” such as binary, octal, and hexadecimal numbers).
However, this brings with it the disadvantage that the common calculation operations and the other Excel functions cannot be used for such values, because the Excel functions require “actual” numbers.
From the polar representation in Figure 17-6, you can see that the location of the complex number z is given by the real part x and the imaginary part y. However, the distance from the origin is not yet known. This distance is the length r in the polar representation (shown on the right in Figure 17-6). r is also called the modulus or the (absolute) value |z| of the complex number z. The absolute value |z| of a complex number is calculated as follows:
This is exactly what the function IMABS() does (see the definition of IMABS() later in this section).
Syntax. COMPLEX(Real_Part,Imaginary_Part,Suffix)
Definition. COMPLEX() links two real numbers to create a complex number. The first number makes up the real part of the complex number x, and the second makes up the imaginary part y (x + yi or x + yj).
Arguments
Real_Part (required) The real part of the complex number you want to build.
Imaginary_Part (required) The imaginary part of the complex number you want to build.
Suffix (optional) The letter you want to use for the imaginary unit of the complex number. If the Suffix argument is not specified, it is assumed to be i.
Important
Complex numbers that are used as arguments in table functions must always be in the algebraic format a + bi. The imaginary unit can optionally be i or j and must be lowercase. Within a function’s arguments list, the case of the imaginary unit must not change.
Background. The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Examples. The following examples illustrate this function.
=COMPLEX(3,–4)returns3–4i.=COMPLEX(3,–4,"j")returns3–4j.
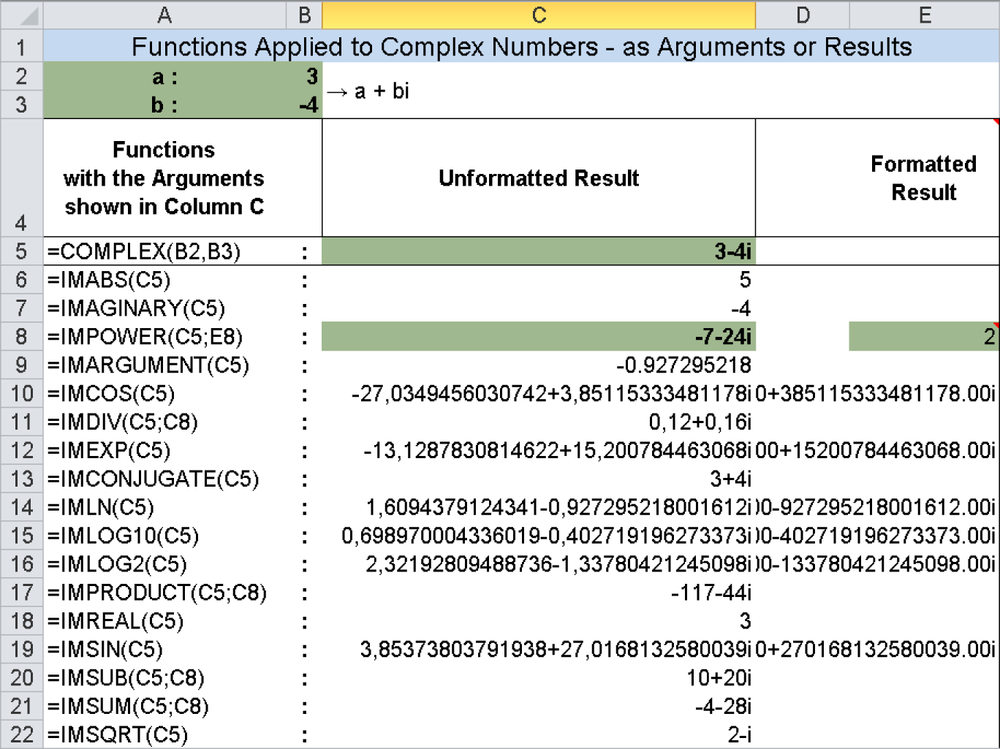
These examples are located among the examples for all of the complex functions in Figure 17-7.
Syntax. IMABS(Complex_Number)
Definition. This function returns the absolute value (modulus) of a complex number. Strings in the format of x + yi or x + yj are accepted.
Argument
Complex_Number (required) The complex number whose absolute value is to be calculated
Note
With the COMPLEX() function, you can build a complex number from one number as the real part and a second number as the imaginary part.
Background. The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates the IMABS() function.
=IMABS("3–4i") returns 5.
Figure 17-7 shows all of the functions for complex numbers, each illustrated with examples. The cells with a shaded background (C5, C8, and E8) contain values that are required as arguments in the various formulas.
Figure 17-7. Overview of all available functions for complex numbers in the Engineering Functions (or Technical Functions) category.
Inside Out: Format complex numbers using a VBA function
Note that the function results are often represented by very long numbers, as you can see in column C of the Excel table shown in Figure 17-7. However, the common formatting options cannot be used for complex numbers, for the reasons mentioned previously.
In this table, a formatting function written in VBA was used. This function was, until recently, provided by Microsoft’s online support.
However, to be able to perform the examples in this book, you don’t need the VBA function and you don’t need any knowledge of VBA. The function is already incorporated in the examples. To use this function, you might need to reduce the macro security in Excel. Otherwise you will receive error messages in column E. In Excel 2010, you can do this with the following steps:
Click the File tab.
Click Options.
Select Trust Center.
Click the Trust Center Settings button.
Click Macro Settings.
Select Enable All Macros.
Click OK twice to confirm.
In Excel 2003 and earlier versions, you might need to set the macro security to medium (or low). If you haven’t done this yet, do the following:
Select Tools/Macro/Security.
In the Security dialog box, select the Medium option.
Click OK to confirm.
The next time you open the Complex.xls workbook, the Security Warning dialog box shown in Figure 17-8 is initially displayed. Clicking the Enable Macros button finally opens the worksheet, activating the VBA module in the background. Now all formulas are completely functional, and you should see the same image as in the example.
Figure 17-8. When a workbook with macros or VBA code is opened in Excel 2003 (or earlier versions), this dialog box is displayed if the macro security level is medium.
When you no longer need the functions that provide macros and VBA modules, you can increase the macro security back to where it was.
Syntax. IMAGINARY(Complex_Number)
Definition. This function returns the imaginary part y of a complex number that is a string in the format x + yi or x + yj.
Note
With the function COMPLEX(), you can build a complex number from one number as the real part and a second as the imaginary part.
Argument
Complex_Number (required) The complex number whose imaginary part is to be determined
Background. The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMAGINARY("3–4i") returns –4.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMARGUMENT(Complex_Number)
Definition. This function returns the argument (Φ) of a complex number, an angle in radians for displaying a complex number in the trigonometric form (see the right side of Figure 17-6, shown earlier in Figure 17-6).
x + yi = |x + yi|·(cosΦ + i · sinΦ)
Argument
Complex_Number (required) The complex number for which you want to determine the argument Φ
Background. The argument (Φ) of a complex number in the format x + yi is calculated as follows:
The basics of complex numbers are described in the section titled Functions for Higher Mathematics.
Example. The following example shows how to use this function.
=IMARGUMENT("3–4i") returns –0.927295218 (the angle Φ in radians).
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMCONJUGATE(Complex_Number)
Definition. This function returns the complex conjugate of a complex number, where the complex number is entered as a string in the format x + yi or x + yj.
Argument
Complex_Number (required) The complex number whose complex conjugate you want to generate
Background. For the complex conjugate 
of a complex number z = x + yi, the following applies:
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example explains this function.
=IMCONJUGATE("3–4i") returns 3+4i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMCOS(Complex_Number)
Definition. This function returns the cosine of a complex number that is a string in the format x + yi or x + yj.
Complex_Number (required) The complex number whose cosine is to be calculated
Background. For the cosine of a complex number, the following applies:
cos(x + yi) = cos(x)·cosh(y)–i·sin(x)·sinh(y)
The basics of complex numbers are described in the section titled Functions for Complex Numbers. Sinh and cosh are the hyperbolic sine and hyperbolic cosine mathematical functions, which you can learn about in Chapter 16.
Example. The following example explains this function.
=IMCOS("3–4i") returns –27.03+3.85i.
This example (with more decimal places) is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMDIV(Complex_Number1,Complex_Number2)
Definition. This function returns the quotient of two complex numbers, which are expected as strings in the format x + yi or x + yj.
Arguments
Complex_Number1 (required) The complex numerator or dividend
Complex_Number2 (required) The complex denominator or divisor
Background. For the quotient z of two complex numbers z1=a+bi and z2=c+di, the following applies:
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMDIV("3–4i","–7–24i") returns 0.12+0.16i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMEXP(Complex_Number)
Definition. This function returns the algebraic form of a complex number z, which is the result of the exponential function with a complex exponent:
z = e(x+yi)
It is therefore the counterpart of the EXP() function, which works with a real number as its argument (z = ex).
The inverse function of IMEXP() is IMLN() (see IMLN()).
Caution
When using the functions IMEXP() and IMLN() for calculating forward and backward, you will notice occasionally that the returned value is not the same as the original one. For example, (1+4i) becomes (–1.77–2.057i) when you use the IMEXP() function. When you take the logarithm of this complex number with the IMLN() function, however, you get (1–2.283i) and not, as expected, the original number of (1+4i).
This (at first glance) strange behavior is a result of the periodicity of the trigonometric functions: With angles of 0° to 360° (or 0 to 2π in radians), the sine runs through values from 0 via 1 back to 0, and then via –1 back to 0. For increasing angles, this sequence is run through repeatedly—periodically with results between –1 and +1.
For the functions IMEXP() and IMLN() to behave reciprocally, the imaginary part y of Complex_Number must be in the range of –π to +π for IMEXP(). If y is outside this range, you will receive unexpected (but correct) results when using the inverse function.
Argument
Complex_Number (required) The exponent of the exponential function, which must be entered as a string in the format x + yi or x + yj
Background. For a complex number in exponential notation, the following applies according to Euler’s formula:
e(x+yi) = ex · eyi = ex · (cos y + i · sin y)
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example describes how to use this function.
=IMEXP("3–4i") returns –13.13+15.20i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMLN(Complex_Number)
Definition. This function returns the natural logarithm of a complex number entered as a string of the format x + yi or x + yj. It is the version of the real LN() function from the Mathematical and Trigonometric Functions category that is to be used for complex numbers.
The IMLN() function is the inverse function of IMEXP(). Be sure to see the Caution about IMEXP() in Caution!
Argument
Complex_Number (required) The complex number whose natural logarithm you want to calculate
Background. The following applies to the natural logarithm of a complex number:
where
(a right half-open interval).
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates how to use this function.
=IMLN("3–4i") returns 1.61–0.93i.
This example (with more decimal places) is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMLOG10(Complex_Number)
Definition. This function returns the base-10 logarithm of a complex number that is entered as a string in the format x + yi or x + yj.
The common logarithm of a complex number can be calculated from the natural logarithm as follows:
log10(x + yi) = log10 e · ln(x +yi)
Argument
Complex_Number (required) The complex number whose common (base 10) logarithm you want to calculate
Background. The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example explains this function.
=IMLOG10("3–4i") returns 0.70–0.40i.
This example (with higher accuracy) is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMLOG2(Complex_Number)
Definition. This function returns the base-2 logarithm of a complex number that is entered as a string in the format x + yi or x + yj.
Argument
Complex_Number (required) The complex number whose base-2 logarithm is to be calculated
Background. The base-2 logarithm of a complex number can be calculated from the natural logarithm as follows:
log2 (x + yi) = log2 e · ln(x + yi)
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMLOG2("3–4i") returns 2.32–1.34i.
This example (with higher accuracy) is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMPOWER(Complex_Number, Power)
Definition. This function exponentiates a complex number, which must be a string of the format x + yi or x + yj, with a real number.
Arguments
Complex_Number (required) The complex number you want to exponentiate.
Power (required) The exponent with which you want to exponentiate the complex number. The argument Power can be an integer, a rational number (a fraction), or negative.
Note
With the COMPLEX() function, you can build a complex number from one number as the real part and a second number as the imaginary part.
Background. The power of a complex number is calculated as follows, using de Moivre’s Formula:
where
and
where
Φ ϵ (–π, π]
(a right half-open interval).
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates how this function is used.
=IMPOWER("3–4i";2) returns –7–24i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMPRODUCT(Complex_Number1,Complex_Number2,...)
Definition. This function returns the product of complex numbers, which are expected as strings in the format x + yi or x + yj.
Arguments
Complex_Number1 (required) and Complex_Number2 (optional) At least one and up to 255 complex numbers that you want to multiply
Background. The product of two complex numbers (a + bi) and (c + di) is calculated as follows:
(a + bi) · (c +di) = (ac – bd) + i · (ad + bc)
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMPRODUCT("3–4i","–1-24i") returns –117–44i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMREAL(Complex_Number)
Definition. This function returns the real part x of a complex number that is a string in the form of x + yi or x + yj.
Argument
Complex_Number (required) The complex number whose real part is to be determined
Background. The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMREAL("3–4i") returns 3.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Definition. This function returns the sine of a complex number, which must be a string in the format x + yi or x + yj.
Argument
Complex_Number (required) The complex number whose sine should be returned
Background. The sine of a complex number is defined as follows:
sin(x + yi) = sin(x) · cosh(y) – i·cos(x)·sinh(y)
The basics of complex numbers are described in the section titled Functions for Complex Numbers in Functions for Complex Numbers. Sinh and cosh are the mathematical functions hyperbolic sine and hyperbolic cosine, which you can learn about in Chapter 16.
Example. The following example illustrates this function.
=IMSIN("3–4i") returns 3.85+27.02i.
This example (with more decimal places) is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMSQRT(Complex_Number)
Definition. This function returns the square root of a complex number (x + yi or x + yj).
Argument
Complex_Number (required) The complex number whose square root is to be determined
Background. The square root of a complex number is calculated as follows:
where
and
where
Φϵ(–π, π]
(a right half-open interval).
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMSQRT("3–4i") returns 2-i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
See Also
IMEXP(), IMLN(), IMLOG10(), IMLOG2() IMPOWER(), SQRT(), Chapter 16
Syntax. IMSUB(Complex_Number1,Complex_Number2)
Definition. This function returns the difference between of two complex numbers, which both need to be strings in the format of x + yi or x + yj.
Arguments
Complex_Number1 (required) The complex number from which Complex_Number2 is to be subtracted
Complex_Number2 (required) The complex number that is to be subtracted from Complex_Number1
Background. The difference between two complex numbers is the difference of the real parts and the difference of the imaginary parts.
(a + bi) – (c + di) = (a – c) + i · (b – d)
This means that the real parts and the imaginary parts of both complex numbers are subtracted separately.
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMSUB("3–4i";"–7–24i") returns 10+20i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
Syntax. IMSUM(Complex_Number1,Complex_Number2,...)
Definition. This function returns the sum of complex numbers, which are expected to be strings of the format x + yi or x + yj.
Arguments
Complex_Number1 (required) and Complex_Number2 (optional) At least one and up to 255 complex numbers to be added
Background. The sum of two complex numbers is calculated by adding the real parts and the imaginary parts separately.
(a + bi) + (c + di) = (a + c) + i·(b + d)
The basics of complex numbers are described in the section titled Functions for Complex Numbers.
Example. The following example illustrates this function.
=IMSUM("3–4i","–7–24i") returns –4–28i.
This example is located among the examples for all of the complex functions, as shown in Figure 17-7.
See Also
IMDIV(), IMPRODUCT(), IMSUB(), SUM(), Chapter 16