Weak encoding means mistakes and weak decoding means illiteracy.
—Rajesh Walecha, Author
An autoencoder is a very simple model: a model that predicts its own input. In fact, it may seem deceivingly simple to the point of being worthless. (After all, what use is a model that predicts what we already know?) Autoencoders are extraordinarily valuable and versatile architectures not because of their functionality to reproduce the input, but because of the internal capabilities developed in order to obtain said functionality. Autoencoders can be chopped up into desirable parts and stuck onto other neural networks, like playing with Legos or performing surgery (take your pick of analogy), with incredible success, or can be used to perform other useful tasks, such as denoising.
This chapter begins by explaining the intuition of the autoencoder concept, followed by a demonstration of how one would implement a simple “vanilla” autoencoder. Afterward, four applications of autoencoders – pretraining, denoising, sparse learning for robust representations, and denoising – are discussed and implemented.
The Concept of the Autoencoder
The operations of encoding and decoding are fundamental to information. Some hypothesize that all transformation and evolution of information results from these two abstracted actions of encoding and decoding (Figures 8-1 and 8-2). Say Alice sees Humpty Dumpty hit his head on the ground after some precarious wall-sitting and tells Bob, “Humpty Dumpty hit his head badly on the ground!” Upon hearing this information, Bob encodes the information from a language representation into thoughts and opinions – what we might call latent representations.
Say Bob is a chef, and so his encoding “specializes” in features relating to food. Bob then decodes the latent representations back into a language representation when he tells Carol, “Humpty Dumpty cracked his shell! We can use the innards to make an omelet.” Carol, in turn, encodes the information.
Say Carol is an egg activist and cares deeply about the well-being of Humpty Dumpty. Her latent representations will encode the information in a way that reflects her priorities and interests as a thinker. When she decodes her latent representations into language, she tells Drew that “People are trying to eat Humpty Dumpty after he has suffered a serious injury! It is horrible.”

A flow diagram depicts the abstract actions of encoding and decoding. The labels are input, encoder, latent space, decoder and output.
A high-level autoencoder architecture

A flow diagram highlights the encoding and decoding transformation results. It exhibits evolution of information from the abstracted actions.
Transformation of information as a series of encoding and decoding operations

A flow diagram depicts the sender and receiver. The sender labels are data, encoding scheme and encrypted while that of receiver are encrypted, decoding scheme and reconstructed data.
Interpretation of autoencoders as sending and receiving encrypted data
Encoding and decoding in deep learning are a bit of a fusion of these two understandings. Autoencoders are versatile neural network structures consisting of an encoder and a decoder component. The encoder maps the input into a smaller latent/encoded space, and the decoder maps the encoded representation back to the original input. The goal of the autoencoder is to reconstruct the original input as faithfully as possible, that is, to minimize the reconstruction loss. In order to do so, the encoder and decoder need to “work together” to develop an encoding and decoding scheme.

A network architecture highlights constant data representation related with the input.
A bad autoencoder architecture (latent space representation size is equal to input representation size)

A network architecture represents expanded data in comparison with the input.
An even worse autoencoder architecture (latent space representation size is larger than input representation size)

A network diagram depicts the compression and reconstruction of the original input.
A good autoencoder architecture (latent space representation size is smaller than input representation size)
Autoencoders are very good at finding higher-level abstractions and features. In order to reliably reconstruct the original input from a much smaller latent space representation, the encoder and decoder must develop a system of mapping that most meaningfully characterizes and distinguishes each input or set of inputs from others. This is no trivial task!

A flow diagram depicts two images, a photograph of a cat on the left and a diagram on the right.
Image-to-text encoding guessing game
Say that you are person B and you are given the following natural language description by person A: “a black pug dressed in a black and white scarf looks at the upper-left region of the camera among an orange background.” For the sake of intuition, it is a worthwhile exercise to try actually playing the role of person B in this game by sketching out/”decoding” the original input.

A photograph of a dog.
What person A was hypothetically looking at when they provided you the natural language encoding. Taken by Charles Deluvio
In this example, the latent space is in the form of language – which is discrete, sequential, and variable-length. Most autoencoders for tabular data use latent spaces that satisfy none of these attributes: they are (quasi-) continuous, read and generated all at once rather than sequentially, and fixed-length. These general autoencoders can reliably find effective encoding and decoding schemes with lifted restrictions, but the two-player game is still good intuition for thinking through challenges associated with autoencoder training.
Although autoencoders are relatively simple neural network architectures, they are incredibly versatile. In this section, we will begin with the plain “vanilla” autoencoder and move to more complex forms and applications of autoencoders.
Vanilla Autoencoders
Let’s begin with the traditional understanding of an autoencoder, which merely consists of an encoder and a decoder component working together to translate the input into a latent representation and then back into original form. The value of autoencoders will become clearer in following sections, in which we will use autoencoders to substantively improve model training.
The goal of this subsection is not only to demonstrate and implement autoencoder architectures but also to understand implementation best practices and to perform technical investigations and explorations into how and why autoencoders work.

An image of a line embedded in a square.
An image of a line
This image contains nine million pixels, meaning we are representing the concept of this line with nine million data values. However, in actuality we can express any line with just four numbers: a slope, a y-intercept, a lower x bound, and a higher x bound (or a starting x point, a starting y point, an ending x point, and an ending y point). If we were to design an encoding and decoding scheme set, the encoder would identify these four parameters – yielding a very compact four-dimensional latent space – and the decoder would redraw the line given those four parameters. By collecting higher-level abstract latent features from the semantics represented in the images, we are able to represent the dataset more compactly. We’ll revisit this example later in the subsection.
Notice, however, that the autoencoder’s reconstruction capability is conditional on the existence of structural similarities (and differences) within the dataset. An autoencoder cannot reliably reconstruct an image of random noise, for instance.
The MNIST dataset is a particularly useful demonstration of autoencoders. It is technically visual/image-based, which is useful for understanding various autoencoder forms and applications (given that autoencoders are most well developed for images). However, it spans a small enough number of features and is structurally simple enough such that we can model it without any convolutional layers. Thus, the MNIST dataset serves as a nice link between the image and tabular data worlds. Throughout this section, we’ll use the MNIST dataset as an introduction to autoencoder techniques before demonstrating applications to “real” tabular/structured datasets.
Loading the MNIST dataset
Building an autoencoder sequentially

A framework architecture visualises features and layers of an autoencoder.
A sequential autoencoder architecture

A bar graph represents the construction of the binary classification of the pixel in its original input. It depicts that maximum values are near 0 or 1.
Distribution of pixel values (scaled between 0 and 1) in the MNIST dataset

A frequency distribution represents the possible values that are not binarised in a complex image datasets.
Distribution of pixel values (scaled between 0 and 1) from a set of images in CIFAR-10

A bar graph represents the distribution of values in tabular datasets.
Distribution of values for a feature in the Higgs Boson dataset (we will work with this dataset later in the chapter)
In these cases, it is more suitable to use a regression loss, like the generic Mean Squared Error or a more specialized alternative (e.g., Huber). Refer to Chapter 1 for a review of regression losses.
Building an autoencoder with compartmentalized design

A visualised architecture model diagram represents the advanced level breakdown of the autoencoder model. It has labels namely the input, encoder sequential and decoder sequential layers.
Visualization of the compartmentalized model
However, using compartmentalized design is incredibly helpful because we can reference the encoder and decoder components separately from the autoencoder. For instance, if we desire to obtain the encoded representation for an input, we can simply call encoder.predict(…) on our input. The encoder and decoder are used to build the autoencoder; after the autoencoder is trained, the encoder and decoder still exist as references to components of that (now trained) autoencoder. The alternative would be to go searching for the latent space layer of the model and create a temporary model to run predictions, in a similar approach to the demonstration in Chapter 4 used to visualize learned convolutional transformations in CNNs. Similarly, if we desire to decode a latent space vector, we can simply call decoder.predict(…) on our sample latent vector.
Visualizing the input, latent space, and reconstruction of an autoencoder

A visualisation of images represents the shape of the internal state of encoder. It exhibits the results from original input, latent space and reconstructed.
Sample latent shape and reconstruction for the digit “7”

A visual representation of reconstruction for the digit 1 created after the training stage.
Sample latent shape and reconstruction for the digit “1”

An image represents the decoding of sample shapes in the latent space and reconstruction stage of the number two. It exhibits the results from original input, latent space, and reconstructed.
Sample latent shape and reconstruction for the digit “2”

An image depicts the reconstruction of the encoder formed after training according to the listing. It exhibits the results from original input, latent space and reconstructed.
Sample latent shape and reconstruction for the digit “5”
When we build standard neural networks that we may want multiple models of with small differences, it is often useful to create a “builder” or “constructor.” The two key parameters of a neural network are the input size and the latent space size. Given these two key “determining’ parameters,” we can infer how we generally want information to flow. For instance, halving the information space in each subsequent layer in the encoder (and doubling in the decoder) is a good generic update rule.

An infographic image represents the intermediate layers that is used to denote nodes as multiples of L.
Visualization of a “halving” autoencoder architecture logic
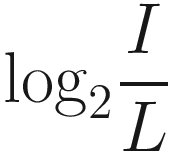
This simple expression measures how many times we need to multiply L by 2 in order to reach I.
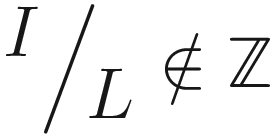 (i.e., I does not divide cleanly into L), in which case our earlier logarithmic expression will not be integer. In these cases, we have a simple fix: we can cast the input to a layer with N nodes, where N = 2k · L for the largest integer k such that N < I. For instance, if I = 4L + 8, we first “cast” down to 4L and execute our standard halving policy from that point (Figure 8-20).
(i.e., I does not divide cleanly into L), in which case our earlier logarithmic expression will not be integer. In these cases, we have a simple fix: we can cast the input to a layer with N nodes, where N = 2k · L for the largest integer k such that N < I. For instance, if I = 4L + 8, we first “cast” down to 4L and execute our standard halving policy from that point (Figure 8-20).
A flow diagram depicts execution of halving policy from the point 4 L.
Adapting the halving autoencoder logic to inputs that are not powers of 2
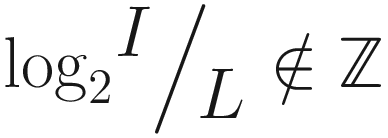 (i.e., we cannot express the input size in relationship to the layer size as an exponent of 2), we can modify our expression for the number of layers required by wrapping with the floor function:
(i.e., we cannot express the input size in relationship to the layer size as an exponent of 2), we can modify our expression for the number of layers required by wrapping with the floor function: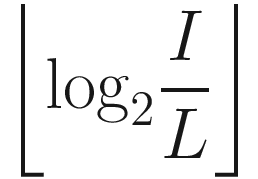
A general function to construct an autoencoder architecture given an input size and a desired latent space, constructed using halving/doubling architectural logic. Note this implementation also has an outActivation parameter in cases where our output is not between 0 and 1
Rather than just returning the model, we also return the encoder and decoder. Recall from earlier discussion of compartmentalized design that retaining a reference to the encoder and decoder components of the autoencoder can be helpful. If not returned, these references – created internally inside the function – will be lost and irretrievable.
Training autoencoders with varying latent space sizes and observing the performance trend

A line graph of validation performance against Latent size represents a sloping curve.
Relationship between the latent size of a tabular autoencoder (2x neurons) and the validation performance. Note the diminishing returns
The diminishing returns for larger latent sizes are very apparently clear. As the latent size increases, the benefit we can reap from it decreases. This phenomenon is true generally in deep learning models (recall “Deep Double Descent” from Chapter 1, which similarly compared model size vs. performance in a supervised domain with CNNs).
Plotting a t-SNE representation of the latent space of autoencoders with varying latent space sizes

A visualisation of variation of latent representation for the given training set.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of two nodes trained on MNIST. Note that in this case, we are projecting into a number of dimensions (2) equal to the dimensionality of the original dataset (2), hence the pretty snake-like arrangements

An image represents size of the bottleneck in relation with the algorithm.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of four nodes trained on MNIST

An image plotted against t S N E and latent space of autoencoders with size of eight nodes.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of eight nodes trained on MNIST

An image within a square represents the bottleneck size of sixteen nodes.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of 16 nodes trained on MNIST

An image represents latent space with the bottleneck size of 32 nodes.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of 32 nodes trained on MNIST

A t S N E projection image depicts the bottleneck size of 64 nodes after training set.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of 64 nodes trained on MNIST

A projection image displays 128 nodes training set that results from an autoencoder.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of 128 nodes trained on MNIST

An image depicts varying shapes resulting from t S N E project of size of 256 nodes.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of 256 nodes trained on MNIST

A visual representation of S N E projection of an autoencoder with bottleneck size of 516 nodes.
t-SNE projection of a latent space for an autoencoder with a bottleneck size of 512 nodes trained on MNIST
If we had loaded the model as model = buildAutoencoder(784, 32)[‘model’] and the encoder as encoder = buildAutoencoder(784, 32)[‘encoder’], we indeed would obtain a model architecture and an encoder architecture – but they wouldn’t be “linked.” The stored model would be associated with an encoder that we haven’t captured, and the stored encoder would be part of an overarching model that we haven’t captured. Thus, we make sure to store the entire set of model components into modelSet first.
Each individual point is colored by the target label (i.e., the digit associated with the data point) for the purpose of exploring the autoencoder’s ability to implicitly “cluster” points of the same digit together or separate them, even though the autoencoder was never exposed to the labels. Observe that as the dimensionality of the latent space increases, the overlap between data samples of different digits decreases until there is functionally complete separation between digits of different classes.
Training and visualizing the latent space of an overcomplete, architecturally redundant autoencoder architecture. This particular architecture has slightly over 5.8 million parameters!

An image visualises compressed latent space reduction. It indicates high performance with low training errors.
t-SNE projection of a latent space for an overcomplete autoencoder with a bottleneck size of 2048 trained on MNIST
Generating a dataset of 50-by-50 images of lines
Fitting a simple autoencoder on the synthetic toy line dataset

An image represents binary cross-entropy that results in accurate reconstructions. It depicts a line in different dimensions.
Left column: original input images of lines. Right column: reconstructions via an autoencoder with a latent space dimensionality of 4

An image represents input received as a straight line from an autoencoder trained set with two neurons.
Left column: original input images of lines. Right column: reconstructions via an autoencoder with a latent space dimensionality of 2
Splitting the dataset into training and validation sets
Fitting an autoencoder on the Mice Protein Expression dataset
Performance of the autoencoder trained on the Mice Protein Expression dataset
Train | Validation | |
|---|---|---|
Mean Squared Error | 0.0117 | 0.0118 |
Mean Absolute Error | 0.0626 | 0.0625 |

A graph represents validation and training performance received after 150 epochs of training sets. It exhibits an L shaped curve.
Training history of an autoencoder trained on the Mice Protein Expression dataset

An image pattern highlights the latent vectors samples and reconstruction created by the autoencoder. It exhibits the vectors into 8 by 10 grids.
Samples and the associated latent vector and reconstruction by an autoencoder trained on the Mice Protein Expression dataset. Samples and reconstructions are represented in two spatial dimensions for convenience of viewing

A scatter diagram visualises data points obtained as a result of tabular autoencoder.
t-SNE projection of a latent space for an autoencoder trained on the Mice Protein Expression dataset
Note that a more formal/rigorous tabular autoencoder design would require us to standardize or normalize all columns to within the same domain. Tabular datasets often contain features that operate on different scales; for instance, say feature A represents a proportion (i.e., between 0 and 1, inclusive), whereas feature B measures years (i.e., likely larger than 1000). Regression losses simply take the mean error across all columns, which means that the reward for correctly reconstructing A is negligible compared to reconstructing feature B. In this case, however, all columns are in roughly the same range, so skipping this step is tolerable.
In the next subsection, we will explore a direct application of autoencoders to concretely improve the performance of supervised models.
Autoencoders for Pretraining
Vanilla autoencoders, as we have already seen, can do some pretty cool things. We see that a vanilla autoencoder trained on various datasets can perform implicit clustering and classification of digits, without being exposed to the labels themselves as well. Rather, natural differences in the input resulting from differences in labels are independently observed and implicitly recognized by the autoencoder.

An infographic image illustrates autoencoder and task training sets. It describes the features of the extractor.
Schematic of multistage pretraining
In the first stage of training, we train the autoencoder on the standard input reconstruction task. After sufficient training, we can extract the encoder and append an “interpretation”-focused model component that assembles and arranges the features extracted by the encoder into the desired output.
During stage 2, we impose layer freezing upon the encoder, meaning that we prevent its weights from being trained. This is to retain the learned structures of the encoder. We spent a significant amount of effort obtaining a good feature extractor; if we do not impose layer freezing, we will find that optimizing a good feature extractor connected to a very poor (randomly initialized) feature interpreter degrades the feature extractor.

A flow diagram depicts the performance achieved as a result of the feature interpreter. It has labels namely primary training and fine-tuning.
Freezing followed by fine-tuning can be an effective way to perform autoencoder pretraining.
Training an autoencoder on MNIST
Repurposing the encoder of the autoencoder as the frozen encoder/feature extractor of a supervised network
Fine-tuning the whole supervised network by unfreezing the encoder
We often reduce the learning rate on fine-tuning tasks to prevent destruction/”overwriting” of information learned during the pretraining process. This can be accomplished by recompiling the model after pretraining with an optimizer configured with a different initial learning rate.
Training a supervised model with the same architecture as the model with pretraining, but without pretraining the encoder via an autoencoding task

A line graph represents the comparison of the given model during the pretraining stage.
Comparing the training curves for a classifier trained on the MNIST dataset with and without autoencoder pretraining
The MNIST dataset is relatively simple, so both models converge relatively quickly to good weights. However, the model with pretraining is noticeably “ahead” of the other. By taking the difference between the epoch at which a model with and without pretraining obtains some performance value, we can estimate how “far ahead” a model with autoencoder pretraining is. For any loss p (at least one epoch in training), the model with pretraining reaches p two to four epochs before the model without pretraining.

A model diagram represents reconstruction tasks that can be used as a basis for generation and text classification.
General transfer learning/pretraining design used dominantly in computer vision
Recall, for instance, the Inception and EfficientNet models discussed in Chapter 4. Keras allows users to load weights from a model trained on ImageNet because the feature extraction “skills” required to perform well on a wide-ranging task like ImageNet are valuable or can be adapted to become valuable in most computer vision tasks.
However, as we have previously seen in Chapters 4 and 5, the success of a deep learning method on complex image and natural language data does not necessarily bar it from being useful to tabular data applications too.
Building and training an autoencoder on the Mice Protein Expression dataset
Using the pretrained encoder in a supervised task

A line graph represents a task model utilising the trained encoder in the frozen and training phases.
Validation and training curves for stages 1 and 2
Defining a custom autoencoder architecture for the Higgs Boson dataset
Using the pretrained encoder as a feature extractor for a supervised task

A line graph represents downward-sloping and erratic curves. It exhibits pre-trained encoder functioning as a feature extractor.
Validation and training loss curves for stages 1 and 2

A line graph represents a rising and erratic curve which makes the static encoder a feature extractor.
Validation and training accuracy curves for stages 1 and 2
We can observe a significant amount of overfitting in this particular case. We can attempt to improve generalization by employing best practices such as adding dropout or batch normalization.
Lastly, it should be noted that using autoencoders for pretraining is a great semi-supervised method. Semi-supervised methods make use of data with and without labels (and are used most often in cases where labeled data is scarce and unlabeled data is abundant). Say you possess three sets of data: Xunlabeled, Xlabeled, and y (which corresponds to Xlabeled). You can train an autoencoder to reconstruct Xunlabeled and then use the frozen encoder as the feature extractor in a task model to predict y from Xlabeled. This technique generally works well even when the size of Xunlabeled is significantly larger than the size of Xlabeled; the autoencoding task learns meaningful representations that should be significantly easier to associate with a supervised target than beginning from initialization.
Multitask Autoencoders

A model represents output dedicated to the task of the autoencoder. It has labels namely the input data, model and task output.
Original task model

A flow diagram depicts the latent features dedicated to the intended task. It has labels namely the input data, encoding layers, and latent space.
Multitask learning
By training the autoencoder simultaneously along the task network, we can theoretically experience the benefits of the autoencoder in a dynamic fashion. Say the encoder has “difficulty” encoding features in a way relevant to the task output, which can be difficult. However, the encoder component of the model can still decrease the overall loss by learning features relevant to the autoencoder reconstruction task. These features may provide continuous support for the task output by providing the optimizer a viable path to loss minimization – it is “another way out,” so to speak. Using multitask autoencoders is often an effective technique to avoid or minimize difficult local minimum problems, in which the model makes mediocre to negligible progress in the first few moments of training and then plateaus (i.e., is stuck in a poor local minimum).
Building a multitask autoencoder for the MNIST dataset

A network architecture depicts the interlinking of functional A P I syntax to create a complete multitask autoencoder.
Visualization of a multitask autoencoder architecture
Compiling and fitting the task model
Plotting out different dimensions of the performance over time

A line graph depicts three different curves. It exhibits a similar pattern.
Different dimensions of performance (reconstruction loss, task loss, overall loss)

An image interprets the performance of the encoder at every epoch.
Multitask autoencoder at zero epochs

An image in a square represents an autoencoder at one epoch.
Multitask autoencoder at one epoch

An image in the shape of the number seven at two epochs.
Multitask autoencoder at two epochs

An output image represents the progression of multitask encoder at several more epochs.
Several more epochs
From these visualizations and the training history, we see that the multitask autoencoder obtains better performance on the task than the autoencoding task that is intended to assist task performance! In this case, the MNIST dataset’s task output is more straightforward than the autoencoding task, which makes sense. In this case, using a multitask autoencoder is not beneficial. It probably is more beneficial to directly train or use an autoencoder for pretraining when multitask autoencoders perform poorly.

A line graph exhibits autoencoding from the training history of the approach on the Mice protection expression dataset.
Different dimensions of performance on the Mice Protein Expression dataset

Four images. 3 grid image visualizes various output state progression values of the set of 80 features and one graph plots the Absolute error, truth and predicted values.
The state of the multitask autoencoder after zero epochs (i.e., upon initialization). Top: displays the original set of 80 features in the Mice Protein Expression dataset (arranged in a grid for more convenient visual viewing), the output of the decoder (of which the goal is to reconstruct the input), and the absolute error of the reconstruction. Bottom: the predicted and true classes (eight in total) and the absolute probability error

Four images. 3 grid images visualize the various outputs obtained after one epoch and one graph plots the Absolute error, truth, and predicted values.
The state of the multitask autoencoder after one epoch

Four images. 3 grid images illustrate the variation in output in a multitask encoder and one graph plots the Absolute error, truth, and predicted values.
The state of the multitask autoencoder after five epochs

Four images. 3 grid images display various encoding features at the original input, decoder output, and other stages and one graph plots the Absolute error, truth, and predicted values.
The state of the multitask autoencoder after 50 epochs
Figures 8-53 through 8-56 demonstrate the performance of the reconstruction task alongside the classification task at various stages in training. Notice that the reconstruction error converges near zero quickly and helps “pull”/”guide” the task error to zero over time.
In many cases, simultaneous execution of the autoencoder task and the original desired task can help provide stimulus to “push” progress on the desired task. However, you may make the valid objection that once the desired task reaches sufficiently good performance, it becomes limited by the autoencoding task.
One method to reconcile with this is simply to detach the autoencoder output from the model by creating a new model connecting the input to the task output and fine-tuning on the dataset.
Another more sophisticated technique is to change the loss weights between the original desired task and the autoencoding task. While Keras weighs multiple losses equally by default, we can provide different weights to reflect different levels of priority or importance delegated to each of the tasks. At the beginning of training, we can give a high weight to the autoencoding task, since we want the model to develop useful representations through a (ideally somewhat easier) task of autoencoding. Throughout the training duration, the weight on the original task model loss can be successively increased and the weight on the autoencoder model loss decreased. To formalize this, let α be the weight on the task output loss, and let 1 − α be the weight on the decoder output loss (with 0 < α < 1).
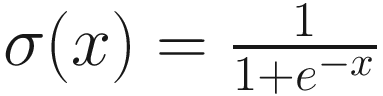 is a pretty good way to get from a value very close to some minimum bound to another value very close to an upper bound. Over the span of 100 epochs, we can employ a simple (arbitrarily set but functional) transformation on the sigmoid function to obtain a smooth transition from a slow to high value of α (visualized by Listing 8-24 in Figure 8-57), where t represents the epoch number:
is a pretty good way to get from a value very close to some minimum bound to another value very close to an upper bound. Over the span of 100 epochs, we can employ a simple (arbitrarily set but functional) transformation on the sigmoid function to obtain a smooth transition from a slow to high value of α (visualized by Listing 8-24 in Figure 8-57), where t represents the epoch number: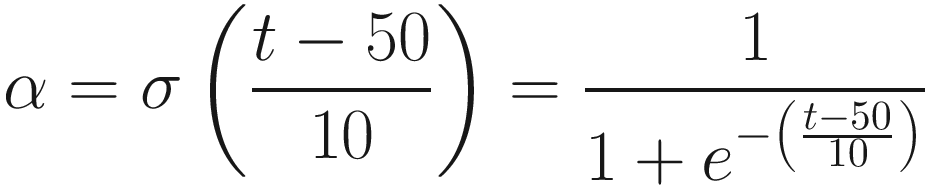

A line graph represents a smooth transition from a slow to a high value of the sigmoid function. It plots the output weight and the decoder output weight.
Plot of the task output loss weight and the decoder weight across each epoch
Plotting out our custom α-adjusting curve
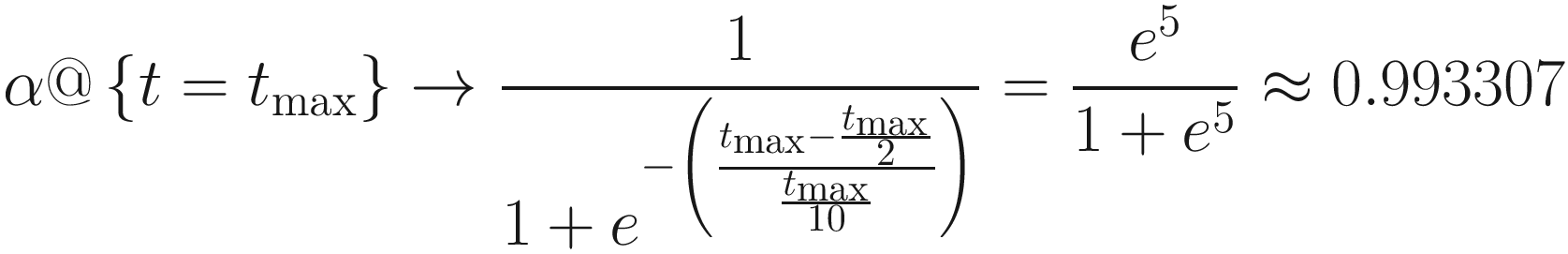
Moreover, we observe by taking the derivative and solving for the maximum that the largest change for some tmax is 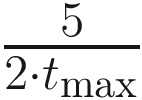 . As tmax increases, analysis of the derivative reveals that the overall change becomes more uniformly spread out. For large values of tmax, this functionally becomes a horizontal line (i.e., the derivative becomes near 0). A simple linear transformation of α also suffices in most cases in which tmax is reasonably large.
. As tmax increases, analysis of the derivative reveals that the overall change becomes more uniformly spread out. For large values of tmax, this functionally becomes a horizontal line (i.e., the derivative becomes near 0). A simple linear transformation of α also suffices in most cases in which tmax is reasonably large.
Recompiling and fitting a multitask autoencoder with varied loss weighting
For another higher-code but perhaps smoother approach to dynamically adjusting the loss calculation weights of multi-output models, which does not require repeated refitting, see Anuj Arora’s well-written post on adaptive loss weighting in Keras using callbacks: https://medium.com/dive-into-ml-ai/adaptive-weighing-of-loss-functions-for-multiple-output-keras-models-71a1b0aca66e.

A diagram interprets the reconstruction task and the total losses incurred through the entire training of the multitask autoencoder.
Diagram of reconstruction loss, task loss, and overall loss (now a dynamically weighted sum) with the weighting gradient shaded in the background
Multitask autoencoders perform best in difficult supervised classification tasks that benefit from rich latent features, which can be learned well by autoencoders.
Sparse Autoencoders

A network architecture exhibits compressed latent space. It indicates data is decoded reliably into the original output.
A standard autoencoder, which encodes information into a densely packed and quasi-continuous latent space

A network diagram exhibits a free pattern that enables the selection of the data of nodes.
A sparse autoencoder, in which a much larger latent size is accessible but only a few nodes can be used at any one time
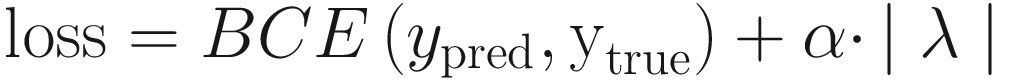
The parameter α is user-defined and controls the “importance” of the L1 regularization term relative to the task loss. Setting the correct value of α is important for correct behavior. If α is too small, the network ignores the sparsity restriction in favor of completing the task, which is now made quasi-trivial by the overcomplete bottleneck layer. If α is too large, the network ignores the task by learning the “ultimate sparsity” – predicting all zeros in the bottleneck layer, which entirely minimizes λ but performs poorly on the actual task we want it to learn.

This is a common machine learning paradigm. L2 regularization tends to produce sets of values generally near zero but not at zero, whereas L1 regularization tends to produce values solidly at zero. An intuitive explanation is that L2 regularization significantly discounts the need to decrease values that are already somewhat near zero. The decrease from 3 to 2, for instance, is rewarded with a penalty decrease of 32 − 22 = 5. The decrease from 1 to 0, on the other hand, is rewarded with a measly penalty decrease of 12 − 02 = 1. On the other hand, L1 regularization rewards the decrease from 3 to 2 identically as the decrease from 1 to 0. We generally use L1 regularization to impose sparsity constraints because of this property.
To implement this, we need to make a slight modification to our original buildAutoencoder function. We can build the autoencoder as if we were leading up to and from a certain implicit latent size, but replace the implicit latent size with the real (expanded) latent size. For instance, consider an autoencoder build with an input of 64 dimensions and an implicit latent space of 8 dimensions. The node count progression in each layer of a standard autoencoder using our prebuilt autoencoder logic would be 64 → 32 → 16 → 8 → 16 → 32 → 64. However, because we are planning to impose a sparsity constraint on the bottleneck layer, we need to provide an expanded set of nodes to pass information through. Say the real bottleneck size is 128 nodes. The node count progression in each layer of this sparse autoencoder would be 64 → 32 → 16 → 128 → 16 → 32 → 64.
Defining a sparse autoencoder with L1 regularization

An interpreter image represents sparse encoder performance on the M N I S T dataset.


Sampled original inputs (left), latent space (middle), and reconstruction (right) for a sparse autoencoder trained on MNIST. The latent space is 256 neurons reshaped into a 16-by-16 grid for viewing. The actual latent space is not arranged in two spatial directions
If we decreased the regularization alpha value (i.e., the L1 penalty would be weighted less relative to the loss), the network would obtain better overall loss at the cost of decreased sparsity (i.e., more nodes would be active at any one pass). If we increased the regularization alpha, the network would obtain worse overall loss at the benefit of increased sparsity (i.e., even fewer nodes would be active at any one pass).

12 Images depict the reshaping of a sparse autoencoder with a latent space of a 16 by 16 grid.

Sampled original inputs (left), latent space (middle), and reconstruction (right) for a sparse autoencoder trained on the Higgs Boson dataset. The latent space is 256 neurons reshaped into a 16-by-16 grid for viewing; the input and reconstruction are 28 dimensions arranged into 7-by-4 grids

12 images represent the utilization of sparse autoencoder to different elements pertaining to the given dataset.

Sampled original inputs (left), latent space (middle), and reconstruction (right) for a sparse autoencoder trained on the Mice Protein Expression dataset. The latent space is 256 neurons reshaped into a 16-by-16 grid for viewing; the input and reconstruction are 80 dimensions arranged into 8-by-10 grids

A mathematical expression. The first input is the photograph of a panda, the second one is a nematode and the output is a gibbon which is depicted by a panda.
Demonstration of the FSGM method. From “Explaining and Harnessing Adversarial Examples,” Goodfellow et al.
Adversarial example finders profit from continuity and gradients. Because neural networks operate in very large continuous spaces, adversarial examples can be found by “sneaking” through smooth channels and ridges in the surface of the landscape. Adversarial examples can be security threats (some instances of naturally occurring adversarial examples, like tape placed onto a traffic sign in a particular orientation causing egregious misidentification), as well as potential symptoms of poor generalization.1 However, sparse encoders impose a discreteness upon the encoded space. It becomes significantly more difficult to generate successful adversarial examples when a frozen encoder is used as the feature extractor for a network.
Sparse autoencoders can also be useful for the purposes of interpretability. We’ll talk more about specialized interpretability techniques later in this chapter, but sparse autoencoders can be easily interpreted without additional complex theoretical tools. Because only a few neurons are active at any one time, understanding which neurons are activated for any one input is relatively simple, especially compared with the latent vectors generated by standard autoencoders.
Denoising and Reparative Autoencoders
So far, we’ve only considered applications of autoencoder training in which the desired output is identical to the input. However, autoencoders can perform another function: to repair or restore a damaged or noisy input.

A flow diagram represents the training dataset to recover a clean image from the artificially corrupted image.
Deriving a noisy image as input and the original clean image as the desired output of a denoising autoencoder

A flow diagram depicts the functioning of the denoising autoencoder. It has the labels input data, denoising autoencoder, model and task output.
A potential application of denoising autoencoders as a structure that learns to clean up the input before it is actually used in a model for a task
These reparative models have particularly exciting applications for intelligent or deep graphics processing. Many graphics operations are not trivially two-way invertible in that it is trivial to go from one state to another but not in the inverse direction. For instance, if I convert a color image or movie into grayscale (for instance, using the pixel-wise methods covered in the image case study in Chapter 2), there is no simple way to invert it back to color. Alternatively, if you spill coffee on an old family photo, there is no trivial process to “erase” the stain.
Autoencoders, however, exploit the triviality of going from the “pure” to the “corrupted” state by artificially imposing corruption upon pure data and forcing powerful autoencoder architectures to learn the “undoing.” Researchers have used denoising autoencoder architectures to generate color versions of historical black-and-white film and to repair photos that have been ripped, stained, or streaked. Another application is in biological/medical imaging, where an imaging operation can be disrupted by environmental conditions; replicating this noise/image damage artificially and training an autoencoder to become robust to it can make the model more resilient to noise.
We will begin with demonstrating the application of a denoising autoencoder to the MNIST dataset by successively increasing the amount of noise in the image and observing how well the denoising autoencoder performs (similarly to exercises in Chapter 4).
Displaying data corrupted by random noise

A numerical grid represents various sample images that have no artificial noise added as a comparison reference.
A grid of untampered clean images from MNIST for reference

A 6 by 6 numerical grid illustrates the images acquired as a result of random noise sampled from a normal distribution with standard deviation.
A sample of MNIST images with added normally distributed random noise using standard deviation 0.1
Training the denoising autoencoder on novel corrupted MNIST data each epoch
Evaluating the performance of the denoising autoencoder on a fresh set of noisy images
Displaying the corrupted image, the reconstruction, and the desired reconstruction (i.e., the original uncorrupted image)

A 3 by 3 grid represents the corrupted images with reference to random noise distributed using a standard deviation.
The noisy/perturbed input (left), the unperturbed desired output (middle), and the predicted output (right) for a denoising autoencoder trained on MNIST with a noisy normal distribution of standard deviation 0.1

A 6 by 6 grid highlights the noise impact on the images with the increase of standard deviation of zero point two.
A sample of MNIST images with added normally distributed random noise using standard deviation 0.2

A 3 by 3 grid represents a set of images displaying reconstruction performance.
The noisy/perturbed input (left), the unperturbed desired output (middle), and the predicted output (right) for a denoising autoencoder trained on MNIST with a noisy normal distribution of standard deviation 0.2

A 6 by 6 numerical grid network exhibits a sample of images that interprets normal distribution.
A sample of MNIST images with added normally distributed random noise using standard deviation 0.3

A 3 by 3 numerical grid interprets images achieved through the performance of a denoising autoencoder that obtains a validation mean absolute error.
The noisy/perturbed input (left), the unperturbed desired output (middle), and the predicted output (right) for a denoising autoencoder trained on MNIST with a noisy normal distribution of standard deviation 0.3

A 6 by 6 grid framework represents images drawn from the standard deviation of zero point five.
A sample of MNIST images with added normally distributed random noise using standard deviation 0.5

A 3 by 3 number grid framework represents noisy input and desired output using denoising autoencoder performance.
The noisy/perturbed input (left), the unperturbed desired output (middle), and the predicted output (right) for a denoising autoencoder trained on MNIST with a noisy normal distribution of standard deviation 0.5

A 6 by 6 number grid of various image patterns acquired as a result of the performance of autoencoder having the denoising feature.
A sample of MNIST images with added normally distributed random noise using standard deviation 0.9

A grid of images represents noisy input, true and predicted denoised output. It depicts the performance of the denoising autoencoder with a standard deviation of 0.9.
The noisy/perturbed input (left), the unperturbed desired output (middle), and the predicted output (right) for a denoising autoencoder trained on MNIST with a noisy normal distribution of standard deviation 0.9
We can see that denoising autoencoders can perform reconstruction to a pretty impressive degree. In practice, however, we want to keep our noise level somewhat low; increasing the noise level can destroy information and cause the network to develop incorrect and/or overly simplified representations of decisions.
A similar logic can be applied to tabular data. There are many situations in which you find that a tabular dataset is particularly noisy. This is especially common in scientific datasets recording variable physical activity, like low-level physics dynamics or biological system data.
Loading and splitting the Mice Protein Expression dataset
Building an autoencoder architecture to fit the Mice Protein Expression dataset
Adding noise to each column of the Mice Protein Expression dataset with a reflective standard deviation
Evaluating the performance of the denoising tabular autoencoder on novel noisy data
After training, the encoder of the denoising autoencoder can be used for pretraining or other previously described applications.
Key Points
Autoencoders are neural network architectures trained to encode an input into a latent space with a representation size smaller than the original input and then to reconstruct the input from the latent space. Autoencoders are forced to learn meaningful latent representations of the data because of this imposed information bottleneck.
The encoder of a trained autoencoder can be detached and built as the feature extractor of a supervised network; that is, the autoencoder serves the purpose of pretraining.
In cases where supervised learning is difficult to get started with, creating a multitask autoencoder that can optimize its loss by performing both the supervised task and an auxiliary autoencoding task can help overcome initial learning hurdles.
Sparse autoencoders use a significantly expanded latent space size, but are trained with restrictions on latent space activity, such that only a few nodes/neurons can be active at any one pass. Sparse autoencoders are thought to be more robust.
Denoising autoencoders are trained to reconstruct clean data from an artificially corrupted, noisy data. In the process, the encoder learns to look for key patterns and “denoises” data, which can be a useful component for supervised models.
In the next chapter, we will look into deep generative models – including a particular type of autoencoder, the Variational Autoencoder (VAE) – which can notably be used to reconcile unbalanced datasets, improve model robustness, and train models on sensitive/private data, in addition to other applications.
