In this chapter, we cover basic equations for rotating two-dimensional points and mapping them on the computer’s screen.
2.1 Rotation Equations

Two-dimensional static coordinate system and a rotated one to calculate coordinates of a point given by a constant position vector P
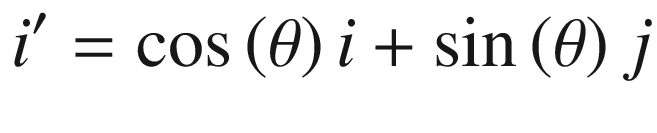
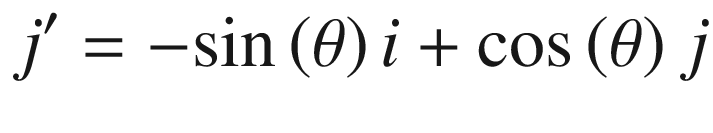
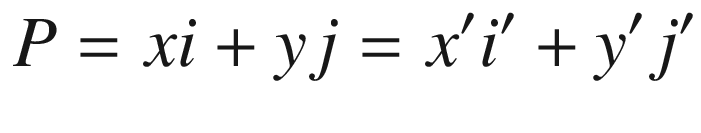
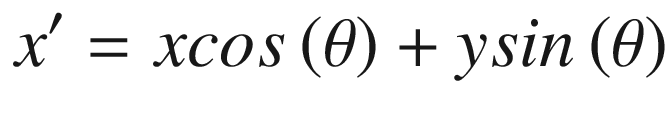
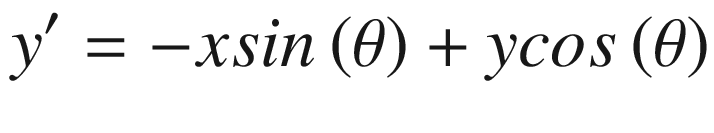
Equations (2.7) and (2.8) are used in our programs to rotate the polygons.
2.2 Mapping Spatial Two-Dimensional Points to the Screen
To correctly map points from a two-dimensional Cartesian coordinate plane to the computer’s screen, it is necessary to consider inherent differences between them. On the Cartesian, two-dimensional plane, a pair of real numbers (x, y) determines the position of a determined point. In contrast, in a computer display, pixels are arranged in a two-dimensional grid in which a pair of integer numbers, which we will denote as (n, m), determines the position of a pixel. The integer n corresponds to the column index of the pixel and m to its row index. Thus, mapping points from a two-dimensional coordinate system to the computer’s screen requires mapping pairs of floating numbers (x, y) to pairs of integer numbers (n, m). Strictly speaking, the function in charge of this task is not bijective.
To obtain analytical relations between the Cartesian coordinate plane and the screen, we first assume that the coordinates of the points on the screen are real numbers rather than integers. This assumption will not alter the results because, in the end, we will take the integer part of the calculated values.
For our calculations, let’s draw two coordinate planes, one below the other, as depicted in Figure 2-2. The upper drawing is a region of a Cartesian coordinate plane around the origin. The lower one consists of a rectangle region on the Cartesian plane resembling the computer’s screen with its center shifted from (0, 0). We want to obtain analytical expressions to map points, from the upper coordinate plane to the ones on the screen on the lower Cartesian plane. The procedure is as follows.
Let’s consider a point on the upper Cartesian (x, y) plane, pointed by vector P and a point with coordinates (xp, yp) pointed by vector Q on the screen, on the lower plane, as shown in Figure 2-2.

Mapping a point with coordinates (x, y) to a point (xp, yp) on the computer’s screen. Vector C points toward the center of the screen
Based on this description, we will write Q = ScaleP. Here, the scale factor is represented by the parameter Scale.


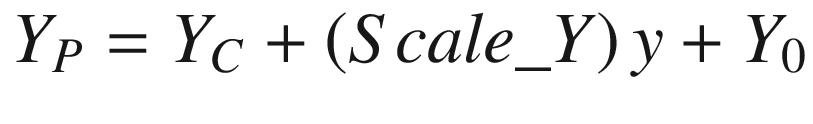
In Equations (2.10) and (2.11), we have increased the scaling options by introducing two independent scaling terms in the x and y directions, Scale _ X and Scale _ Y. Since we need to shift the points to other regions of the screen, we have introduced additional shifting parameters, (X0, Y0).
Equations (2.7)-(2.8) and (2.10)-(2.11) can be used for constructing and rotating polygons in a two-dimensional space and displaying them on the computer’s screen. In the following chapter, we illustrate the use of these equations.
2.3 Summary
In this chapter, we obtained analytical equations for rotating points in a two-dimensional Cartesian plane. Additionally, we derived analytical equations for mapping them on the computer’s screen. These equations are used in the following chapter to construct two-dimensional polygons in a two-dimensional coordinate system to be displayed and rotated on the computer’s screen.

![$$ P= xi+ yj={x}^{prime}left[mathit{cos}left( heta
ight)i+mathit{sin}left( heta
ight)j
ight]+{y}^{prime}left[-mathit{sin}left( heta
ight)i+mathit{cos}left( heta
ight)j
ight] $$](https://imgdetail.ebookreading.net/202109/3/9781484271131/9781484271131__9781484271131__files__images__510726_1_En_2_Chapter__510726_1_En_2_Chapter_TeX_Equ4.png)

