16
Model Diagnostics
Building models is a continuous art. As we start adding and removing variables from our models, we need a means to compare models with one another and a consistent way of measuring model performance. There are many ways we can compare models, and this chapter describes some of these methods.
16.1 Residuals
The residuals of a model compare what the model calculates and the actual values in the data. Let’s fit some models on a housing data set.
import pandas as pd
housing = pd.read_csv('data/housing_renamed.csv')
print(housing.head()) neighborhood type units year_built sq_ft income
0 FINANCIAL R9-CONDOMINIUM 42 1920.0 36500 1332615
1 FINANCIAL R4-CONDOMINIUM 78 1985.0 126420 6633257
2 FINANCIAL RR-CONDOMINIUM 500 NaN 554174 17310000
3 FINANCIAL R4-CONDOMINIUM 282 1930.0 249076 11776313
4 TRIBECA R4-CONDOMINIUM 239 1985.0 219495 10004582 income_per_sq_ft expense expense_per_sq_ft net_income
0 36.51 342005 9.37 990610
1 52.47 1762295 13.94 4870962
2 31.24 3543000 6.39 13767000
3 47.28 2784670 11.18 8991643
4 45.58 2783197 12.68 7221385 value value_per_sq_ft boro
0 7300000 200.00 Manhattan
1 30690000 242.76 Manhattan
2 90970000 164.15 Manhattan
3 67556006 271.23 Manhattan
4 54320996 247.48 ManhattanWe’ll begin with a multiple linear regression model with three covariates.
import statsmodels
import statsmodels.api as sm
import statsmodels.formula.api as smf
house1 = smf.glm(
"value_per_sq_ft ~ units + sq_ft + boro", data=housing
).fit()
print(house1.summary()) Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: value_per_sq_ft No. Observations: 2626
Model: GLM Df Residuals: 2619
Model Family: Gaussian Df Model: 6
Link Function: identity Scale: 1879.5
Method: IRLS Log-Likelihood: -13621.
Date: Thu, 01 Sep 2022 Deviance: 4.9224e+06
Time: 01:55:55 Pearson chi2: 4.92e+06
No. Iterations: 3 Pseudo R-squ. (CS): 0.7772
Covariance Type: nonrobust
=========================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------------
Intercept 43.2909 5.330 8.122 0.000 32.845 53.737
boro[T.Brooklyn] 34.5621 5.535 6.244 0.000 23.714 45.411
boro[T.Manhattan] 130.9924 5.385 24.327 0.000 120.439 141.546
boro[T.Queens] 32.9937 5.663 5.827 0.000 21.895 44.092
boro[T.Staten Island] -3.6303 9.993 -0.363 0.716 -23.216 15.956
units -0.1881 0.022 -8.511 0.000 -0.231 -0.145
sq_ft 0.0002 2.09e-05 10.079 0.000 0.000 0.000
=========================================================================================We can plot the residuals of our model (Figure 16.1). What we are looking for is a plot with a random scattering of points. If a pattern is apparent, then we will need to investigate our data and model to see why this pattern emerged.
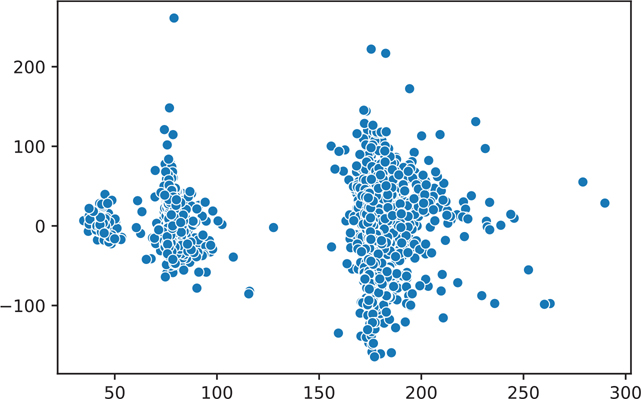
Figure 16.1 Residuals of the house1 model
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
sns.scatterplot(
x=house1.fittedvalues, y=house1.resid_deviance, ax=ax
)
plt.show()This residual plot is concerning because it contains obvious clusters and groups (residual plots are supposed to look random). We can color our plot by the boro variable, which indicates the borough of New York where the data apply (Figure 16.2).
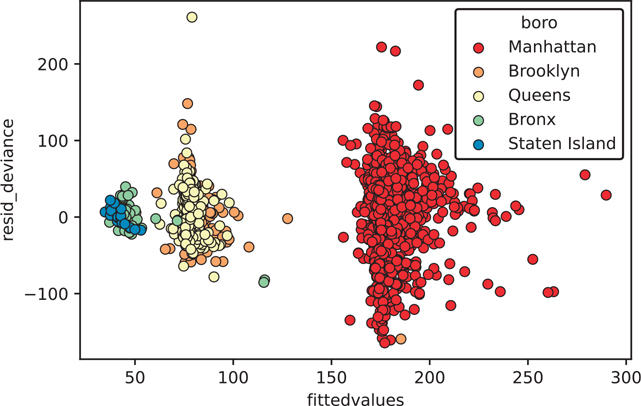
Figure 16.2 Residuals of the house1 model colored by boro
# get the data used for the residual plot and boro color
res_df = pd.DataFrame(
{
"fittedvalues": house1.fittedvalues, # get a model attribute
"resid_deviance": house1.resid_deviance,
"boro": housing["boro"], # get a value from data column
}
)
# greyscale friendly color palette
color_dict = dict(
{
"Manhattan": "#d7191c",
"Brooklyn": "#fdae61",
"Queens": "#ffffbf",
"Bronx": "#abdda4",
"Staten Island": "#2b83ba",
}
)
fig, ax = plt.subplots()
fig = sns.scatterplot(
x="fittedvalues",
y="resid_deviance",
data=res_df,
hue="boro",
ax=ax,
palette=color_dict,
edgecolor='black',
)
plt.show()When we color our points based on boro, you can see that the clusters are highly governed by the value of this variable.
16.1.1 Q-Q Plots
A q-q plot is a graphical technique that determines whether your data conforms to a reference distribution. Since many models assume the data is normally distributed, a q-q plot is one way to make sure your data really is normal (Figure 16.3).
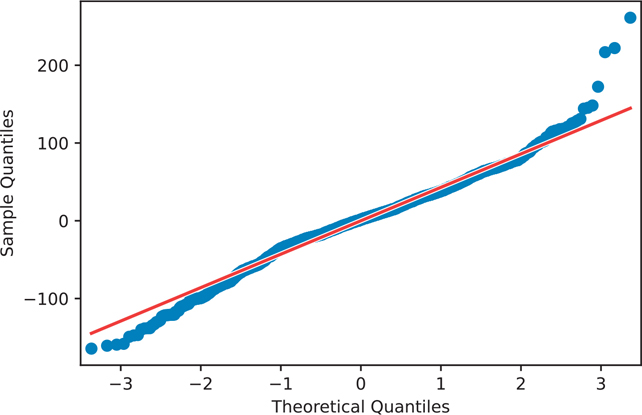
Figure 16.3 The q-q plot of the house1 model
from scipy import stats
# make a copy of the variable so we don't need to keep typing it
resid = house1.resid_deviance.copy()fig = statsmodels.graphics.gofplots.qqplot(resid, line='r')
plt.show()We can also plot a histogram of the residuals to see if our data is normal (Figure 16.4).
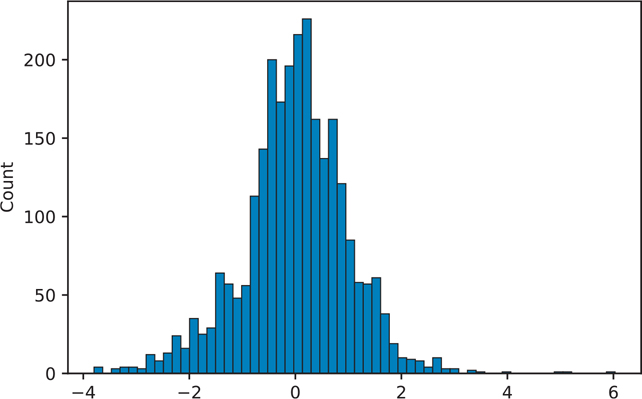
Figure 16.4 Histogram of the house1 model residuals
resid_std = stats.zscore(resid)
fig, ax = plt.subplots()
sns.histplot(resid_std, ax=ax)
plt.show()If the points on the q-q plot lie on the red line, that means our data match our reference distribution. If the points do not lie on this line, then one thing we can do is apply a transformation to our data. Table 16.1 shows which transformations can be performed on our data. If the q-q plot of points is convex compared to the red reference line, then you can transform your data toward the top of the table. If the q-q plot of points is concave compared to the red reference line, then you can transform your data toward the bottom of the table.
Table 16.1 Transformations
xp | Equivalent | Description |
x2 | x2 | Square |
x1 | x |
|
Square root | ||
“x”x | log(x) | Log |
Reciprocal square root | ||
x−1 | Reciprocal | |
x−2 | Reciprocal square |
16.2 Comparing Multiple Models
Now that we know how to assess a single model, we need a means to compare multiple models so that we can pick the “best” one.
16.2.1 Working with Linear Models
We begin by fitting five models. Note that some of the models use the + operator to add covariates to the model, whereas others use the * operator. To specify an interaction in our model, we use the * operator. That is, the variables that are interacting are behaving in a way that is not independent of one another, but in such a way that their values affect one another and are not simply additive.
f1 = 'value_per_sq_ft ~ units + sq_ft + boro'
f2 = 'value_per_sq_ft ~ units * sq_ft + boro'
f3 = 'value_per_sq_ft ~ units + sq_ft * boro + type'
f4 = 'value_per_sq_ft ~ units + sq_ft * boro + sq_ft * type'
f5 = 'value_per_sq_ft ~ boro + type'
house1 = smf.ols(f1, data=housing).fit()
house2 = smf.ols(f2, data=housing).fit()
house3 = smf.ols(f3, data=housing).fit()
house4 = smf.ols(f4, data=housing).fit()
house5 = smf.ols(f5, data=housing).fit()With all our models, we can collect all of our coefficients and the model with which they are associated.
mod_results = (
pd.concat(
[
house1.params,
house2.params,
house3.params,
house4.params,
house5.params,
],
axis=1,
)
.rename(columns=lambda x: "house" + str(x + 1))
.reset_index()
.rename(columns={"index": "param"})
.melt(id_vars="param", var_name="model", value_name="estimate")
)print(mod_results) param model estimate
0 Intercept house1 43.290863
1 boro[T.Brooklyn] house1 34.562150
2 boro[T.Manhattan] house1 130.992363
3 boro[T.Queens] house1 32.993674
4 boro[T.Staten Island] house1 -3.630251
.. ... ... ...
85 sq_ft:boro[T.Queens] house5 NaN
86 sq_ft:boro[T.Staten Island] house5 NaN
87 sq_ft:type[T.R4-CONDOMINIUM] house5 NaN
88 sq_ft:type[T.R9-CONDOMINIUM] house5 NaN
89 sq_ft:type[T.RR-CONDOMINIUM] house5 NaN[90 rows x 3 columns]Since it’s not very useful to look at a large column of values, we can plot our coefficients to quickly see how the models are estimating parameters in relation to each other (Figure 16.5).
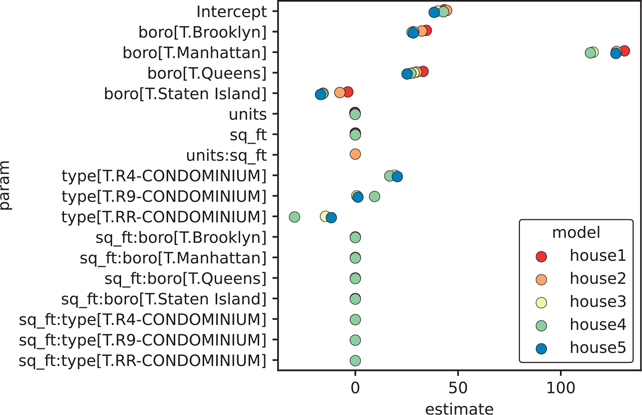
Figure 16.5 Coefficients of the house1 to house5 models
color_dict = dict(
{
"house1": "#d7191c",
"house2": "#fdae61",
"house3": "#ffffbf",
"house4": "#abdda4",
"house5": "#2b83ba",
}
)fig, ax = plt.subplots()
ax = sns.pointplot(
x="estimate",
y="param",
hue="model",
data=mod_results,
dodge=True, # jitter the points
join=False, # don't connect the points
palette=color_dict
)
plt.tight_layout()
plt.show()Now that we have our linear models, we can use the analysis of variance (ANOVA) method to compare them. The ANOVA will give us the residual sum of squares (RSS), which is one way we can measure performance (lower is better).
model_names = ["house1", "house2", "house3", "house4", "house5"]
house_anova = statsmodels.stats.anova.anova_lm(
house1, house2, house3, house4, house5
)
house_anova.index = model_names
print(house_anova) df_resid ssr df_diff ss_diff F
house1 2619.0 4.922389e+06 0.0 NaN NaN
house2 2618.0 4.884872e+06 1.0 37517.437605 20.039049
house3 2612.0 4.619926e+06 6.0 264945.539994 23.585728
house4 2609.0 4.576671e+06 3.0 43255.441192 7.701289
house5 2618.0 4.901463e+06 -9.0 -324791.847907 19.275539 Pr(>F)
house1 NaN
house2 7.912333e-06
house3 2.754431e-27
house4 4.025581e-05
house5 NaNAnother way we can calculate model performance is by using the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). These methods apply a penalty for each feature that is added to the model (lower AIC and BIC value is better). Thus, we should strive to balance performance and parsimony.
house_models = [house1, house2, house3, house4, house5]abic = pd.DataFrame(
{
"model": model_names,
"aic": [mod.aic for mod in house_models],
"bic": [mod.bic for mod in house_models],
}
)
print(abic.sort_values(by=["aic", "bic"])) model aic bic
3 house4 27084.800043 27184.644733
2 house3 27103.502577 27185.727615
1 house2 27237.939618 27284.925354
4 house5 27246.843392 27293.829128
0 house1 27256.031113 27297.14363216.2.2 Working with GLM Models
We can perform the same calculations and model diagnostics on generalized linear models (GLMs). We can use the deviance of the model to do model comparisons:
def deviance_table( *models):
"""Create a table of model diagnostics from model objects"""
return pd.DataFrame(
{
"df_residuals": [mod.df_resid for mod in models],
"resid_stddev": [mod.deviance for mod in models],
"df": [mod.df_model for mod in models],
"deviance": [mod.deviance for mod in models],
}
)f1 = 'value_per_sq_ft ~ units + sq_ft + boro'
f2 = 'value_per_sq_ft ~ units * sq_ft + boro'
f3 = 'value_per_sq_ft ~ units + sq_ft * boro + type'
f4 = 'value_per_sq_ft ~ units + sq_ft * boro + sq_ft * type'
f5 = 'value_per_sq_ft ~ boro + type'
glm1 = smf.glm(f1, data=housing).fit()
glm2 = smf.glm(f2, data=housing).fit()
glm3 = smf.glm(f3, data=housing).fit()
glm4 = smf.glm(f4, data=housing).fit()
glm5 = smf.glm(f5, data=housing).fit()
glm_anova = deviance_table(glm1, glm2, glm3, glm4, glm5)
print(glm_anova) df_residuals resid_stddev df deviance
0 2619 4.922389e+06 6 4.922389e+06
1 2618 4.884872e+06 7 4.884872e+06
2 2612 4.619926e+06 13 4.619926e+06
3 2609 4.576671e+06 16 4.576671e+06
4 2618 4.901463e+06 7 4.901463e+06We can do the same set of calculations in a logistic regression.
# create a binary variable
housing["high"] = (housing["value_per_sq_ft"] >= 150).astype(int)
print(housing["high"].value_counts())0 1619
1 1007
Name: high, dtype: int64# create and fit our logistic regression using GLM
f1 = "high ~ units + sq_ft + boro"
f2 = "high ~ units * sq_ft + boro"
f3 = "high ~ units + sq_ft * boro + type"
f4 = "high ~ units + sq_ft * boro + sq_ft * type"
f5 = "high ~ boro + type"logistic = statsmodels.genmod.families.family.Binomial(
link=statsmodels.genmod.families.links.Logit()
)
glm1 = smf.glm(f1, data=housing, family=logistic).fit()
glm2 = smf.glm(f2, data=housing, family=logistic).fit()
glm3 = smf.glm(f3, data=housing, family=logistic).fit()
glm4 = smf.glm(f4, data=housing, family=logistic).fit()
glm5 = smf.glm(f5, data=housing, family=logistic).fit()# show the deviances from our GLM models
print(deviance_table(glm1, glm2, glm3, glm4, glm5)) df_residuals resid_stddev df deviance
0 2619 1695.631547 6 1695.631547
1 2618 1686.126740 7 1686.126740
2 2612 1636.492830 13 1636.492830
3 2609 1619.431515 16 1619.431515
4 2618 1666.615696 7 1666.615696Finally, we can create a table of AIC and BIC values.
mods = [glm1, glm2, glm3, glm4, glm5]
abic_glm = pd.DataFrame(
{
"model": model_names,
"aic": [mod.aic for mod in house_models],
"bic": [mod.bic for mod in house_models],
}
)
print(abic_glm.sort_values(by=["aic", "bic"])) model aic bic
3 house4 27084.800043 27184.644733
2 house3 27103.502577 27185.727615
1 house2 27237.939618 27284.925354
4 house5 27246.843392 27293.829128
0 house1 27256.031113 27297.143632Looking at all these measures, we can say Model 4 is performing the best so far.
16.3 k-Fold Cross-Validation
Cross-validation is another technique to compare models. One of the main benefits is that it can account for how well your model performs on new data. It does this by partitioning your data into k parts. It holds one of the parts aside as the “test” set and then fits the model on the remaining k − 1 parts, the “training” set. The fitted model is then used on the “test” and an error rate is calculated. This process is repeated until all k parts have been used as a “test” set. The final error of the model is some average across all the models.
Cross-validation can be performed in many different ways. The method just described is called “k-fold cross-validation.” Alternative ways of performing cross-validation include “leave-one-out cross-validation”, in which the training data consists of all the data except one observation designated as the test set.
Here we will split our data into k − 1 testing and training data sets.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
print(housing.columns)Index(['neighborhood', 'type', 'units', 'year_built', 'sq_ft',
'income', 'income_per_sq_ft', 'expense', 'expense_per_sq_ft',
'net_income', 'value', 'value_per_sq_ft', 'boro', 'high'],
dtype='object')# get training and test data
X_train, X_test, y_train, y_test = train_test_split(
pd.get_dummies(
housing[["units", "sq_ft", "boro"]], drop_first=True
),
housing["value_per_sq_ft"],
test_size=0.20,
random_state=42,
)We can get a score that indicates how well our model is performing using our test data.
lr = LinearRegression().fit(X_train, y_train)
print(lr.score(X_test, y_test))0.6137125285030868Since sklearn relies heavily on the numpy ndarray, the patsy library allows you to specify a formula just like the formula API in statsmodels, and it returns a proper numpy array you can use in sklearn.
Here is the same code as before, but using the dmatrices function in the patsy library.
from patsy import dmatrices
y, X = dmatrices(
"value_per_sq_ft ~ units + sq_ft + boro",
housing,
return_type="dataframe",
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=42
)
lr = LinearRegression().fit(X_train, y_train)
print(lr.score(X_test, y_test))0.6137125285030818To perform a k-fold cross-validation, we need to import this function from sklearn.
from sklearn.model_selection import KFold, cross_val_score
# get a fresh new housing data set
housing = pd.read_csv('data/housing_renamed.csv')We now have to specify how many folds we want. This number depends on how many rows of data you have. If your data does not include too many observations, you may opt to select a smaller k (e.g., 2). Otherwise, a k between 5 to 10 is fairly common. However, keep in mind that the trade-off with higher k values is more computation time.
kf = KFold(n_splits=5)
y, X = dmatrices('value_per_sq_ft ~ units + sq_ft + boro', housing)Next we can train and test our model on each fold.
coefs = []
scores = []
for train, test in kf.split(X):
X_train, X_test = X[train], X[test]
y_train, y_test = y[train], y[test]
lr = LinearRegression().fit(X_train, y_train)
coefs.append(pd.DataFrame(lr.coef_))
scores.append(lr.score(X_test, y_test))We can also view the results.
coefs_df = pd.concat(coefs)
coefs_df.columns = X.design_info.column_names
print(coefs_df) Intercept boro[T.Brooklyn] boro[T.Manhattan] boro[T.Queens]
0 0.0 33.369037 129.904011 32.103100
0 0.0 32.889925 116.957385 31.295956
0 0.0 30.975560 141.859327 32.043449
0 0.0 41.449196 130.779013 33.050968
0 0.0 -38.511915 56.069855 -17.557939
boro[T.Staten Island] units sq_ft
0 -4.381085e+00 -0.205890 0.000220
0 -4.919232e+00 -0.146180 0.000155
0 -4.379916e+00 -0.179671 0.000194
0 -3.430209e+00 -0.207904 0.000232
0 3.552714e-15 -0.145829 0.000202We can take a look at the average coefficient across all folds using .apply() and the np.mean() function.
import numpy as np
print(coefs_df.apply(np.mean))Intercept 0.000000
boro[T.Brooklyn] 20.034361
boro[T.Manhattan] 115.113918
boro[T.Queens] 22.187107
boro[T.Staten Island] -3.422088
units -0.177095
sq_ft 0.000201
dtype: float64We can also look at our scores. Each model has a default scoring method. LinearRegression(), for example, uses the R2 (coefficient of determination) regression score function.1
print(scores)[0.02731416291043942, -0.5538362212110504, -0.1563637168806138,
-0.3234202061929452, -1.6929655586752923]We can also use cross_val_scores (for cross-validation scores) to calculate our scores.
# use cross_val_scores to calculate CV scores
model = LinearRegression()
scores = cross_val_score(model, X, y, cv=5)
print(scores)[ 0.02731416 -0.55383622 -0.15636372 -0.32342021 -1.69296556]1. Scikit-learn R2 scoring: https://scikit-learn.org/stable/modules/generated/sklearn.metrics.r2_score.html
When we compare multiple models to one another, we compare the average of the scores.
print(scores.mean())-0.5398543080098925Now we’ll refit all our models using k-fold cross-validation.
# create the predictor and response matrices
y1, X1 = dmatrices(
"value_per_sq_ft ~ units + sq_ft + boro", housing)
y2, X2 = dmatrices("value_per_sq_ft ~ units*sq_ft + boro", housing)
y3, X3 = dmatrices(
"value_per_sq_ft ~ units + sq_ft*boro + type", housing
)
y4, X4 = dmatrices(
"value_per_sq_ft ~ units + sq_ft*boro + sq_ft*type", housing
)
y5, X5 = dmatrices("value_per_sq_ft ~ boro + type", housing)# fit our models
model = LinearRegression()
scores1 = cross_val_score(model, X1, y1, cv=5)
scores2 = cross_val_score(model, X2, y2, cv=5)
scores3 = cross_val_score(model, X3, y3, cv=5)
scores4 = cross_val_score(model, X4, y4, cv=5)
scores5 = cross_val_score(model, X5, y5, cv=5)We can now look at our cross-validation scores.
scores_df = pd.DataFrame(
[scores1, scores2, scores3, scores4, scores5]
)
print(scores_df.apply(np.mean, axis=1))0 -5.398543e-01
1 -1.088184e+00
2 -8.668885e+25
3 -7.634198e+25
4 -3.172546e+25
dtype: float64Once again, we see that Model 4 has the best performance.
Conclusion
When we are working with models, it’s important to measure their performance. Using ANOVA for linear models, looking at deviance for GLM models, and using cross-validation are all ways we can measure error and performance when trying to pick the best model.
