Understanding Recursion

Recursion is useful for tasks that can be defined in terms of similar subtasks. For example, sort, search, and traversal problems often have simple recursive solutions. A recursive function performs a task in part by calling itself to perform the subtasks. At some point, the function encounters a subtask that it can perform without calling itself. This case, in which the function does not recurse, is called the base case; the former, in which the function calls itself to perform a subtask, is referred to as the recursive case.

These concepts can be illustrated with a simple and commonly used example: the factorial operator. n! (pronounced “n factorial”) is the product of all integers between n and 1. For example, 4! = 4 × 3 × 2 × 1 = 24. n! can be more formally defined as follows:

n! = n (n – 1)!

0! = 1! = 1

This definition leads easily to a recursive implementation of factorial. The task is to determine the value of n!, and the subtask is to determine the value of (n – 1)! . In the recursive case, when n is greater than 1, the function calls itself to determine the value of (n – 1)! and multiplies that by n. In the base case, when n is 0 or 1, the function simply returns 1. Rendered in code, this looks like the following:

int factorial( int n ){
    if (n > 1) {    /* Recursive case */
        return factorial(n-1) * n;
    } else {        /* Base case */
        return 1;
    }
}

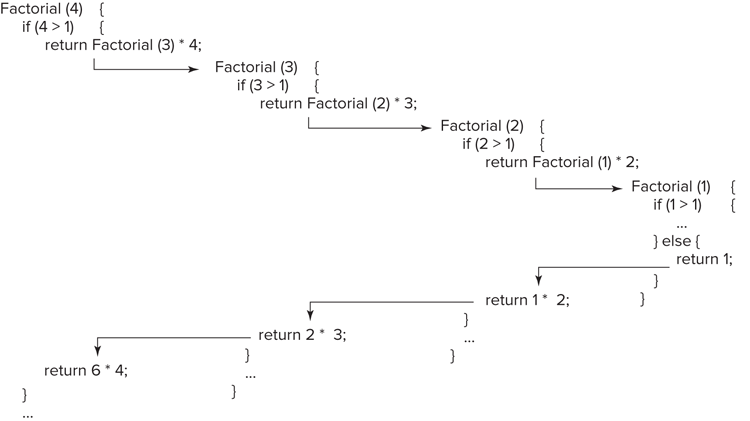
Figure 7-1 illustrates the operation of this function when computing 4!. Notice that n decreases by 1 each time the function recurses. This ensures that the base case will eventually be reached. If a function is written incorrectly such that it does not always reach a base case, it recurses infinitely. In practice, there is usually no such thing as infinite recursion: Eventually a stack overflow occurs and the program crashes — a similarly catastrophic event.

Figure 7-1

Note that when the value returned by the recursive call is itself immediately returned, as in the preceding definition for factorial, the function is tail-recursive. Some compilers can perform tail call elimination on tail-recursive functions, an optimization that reuses the same stack frame for each recursive call. An appropriately optimized tail-recursive function could recurse infinitely without overflowing the stack.

This implementation of factorial represents an extremely simple example of a recursive function. In many cases, your recursive functions may need additional data structures or an argument that tracks the recursion level. Often the best solution in such cases is to move the data structure or argument initialization code into a separate function. This wrapper function, which performs initialization and then calls the purely recursive function, provides a clean, simple interface to the rest of the program.

For example, if you need a factorial function that returns all its intermediate results (factorials less than n), as well as the final result (n!), you most naturally return these results as an integer array, which means the function needs to allocate an array. You also need to know where in the array each result should be written. These tasks are easily accomplished using a wrapper function, as follows:

int[] allFactorials( int n ){ /* Wrapper function */
    int[] results = new int[ n == 0 ? 1 : n ];
    doAllFactorials( n, results, 0 );
    return results;
}
int doAllFactorials( int n, int[] results, int level ){
    if( n > 1 ){  /* Recursive case */
        results[level] = n * doAllFactorials( n - 1, results, level + 1 );
        return results[level];
    } else {        /* Base case */
        results[level] = 1;
        return 1;
    }
}

You can see that using a wrapper function enables you to hide the array allocation and recursion level tracking to keep the recursive function clean. In this case, you can determine the appropriate array index from n, avoiding the need for the level argument, but in many cases there is no alternative to tracking the recursion level, as shown here.

Although recursion is a powerful technique, it is not always the best approach, and rarely is it the most efficient approach. This is due to the relatively large overhead for function calls on most platforms. For a simple recursive function like factorial, many computer architectures spend more time on call overhead than on the actual calculation. Iterative functions, which use looping constructs instead of recursive function calls, do not suffer from this overhead and are frequently more efficient.

Any problem that can be solved recursively can also be solved iteratively. Iterative algorithms are often easy to write, even for tasks that might appear to be fundamentally recursive. For example, an iterative implementation of factorial is relatively simple. It may be helpful to reframe the definition of factorial, such that you describe n! as the product of every integer between n and 1, inclusive. You can use a for loop to iterate through these values and calculate the product:

int factorial( int n ){
    int i, val = 1;
    for( i = n; i > 1; i-- )  /* n = 0 or 1 falls through */
        val *= i;
    return val;
}

This implementation is significantly more efficient than the previous recursive implementation because it doesn’t make any additional function calls. Although it represents a different way of thinking about the problem, it’s not any more difficult to write than the recursive implementation.

For some problems, obvious iterative alternatives like the one just shown don’t exist, but it’s always possible to implement a recursive algorithm without using recursive calls. Recursive calls are generally used to preserve the current values of local variables and restore them when the subtask performed by the recursive call is completed. Because local variables are allocated on the program’s stack, each recursive instance of the routine has a separate set of the local variables, so recursive calls implicitly store variable values on the program’s stack. You can eliminate the need for recursive calls by allocating your own stack and manually storing and retrieving local variable values from this stack.

Implementing this type of stack-based iterative function tends to be significantly more complicated than implementing an equivalent function using recursive calls. Furthermore, unless the overhead for the stack you use is significantly less than the function call overhead, a function written this way won’t be more efficient than a conventional recursive implementation. Therefore you should implement recursive algorithms with recursive calls unless instructed otherwise. An example of a recursive algorithm implemented without recursive calls is given in the solution to the “Preorder Traversal, No Recursion” problem in Chapter 5.

In an interview, a working solution is of primary importance; an efficient solution is secondary. Unless you’ve been told otherwise, go with whatever type of working solution comes to you first. If it’s a recursive solution, you might want to mention the inefficiencies inherent in recursive solutions to your interviewer, so it’s clear that you know about them. In the rare instance that you see a recursive solution and an iterative solution of roughly equal complexity, you should probably mention them both to the interviewer, indicating that you’re going to work out the iterative solution because it’s likely to be more efficient.