Column 2: Aha! Algorithms

The study of algorithms offers much to the practicing programmer. A course on the subject equips students with functions for important tasks and techniques for attacking new problems. We’ll see in later columns how advanced algorithmic tools sometimes have a substantial influence on software systems, both in reduced development time and in faster execution speed.

As crucial as those sophisticated ideas are, algorithms have a more important effect at a more common level of programming. In his book Aha! Insight (from which I stole my title), Martin Gardner describes the contribution I have in mind: “A problem that seems difficult may have a simple, unexpected solution.” Unlike the advanced methods, the aha! insights of algorithms don’t come only after extensive study; they’re available to any programmer willing to think seriously before, during and after coding.

A. Given a sequential file that contains at most four billion 32-bit integers in random order, find a 32-bit integer that isn’t in the file (and there must be at least one missing — why?). How would you solve this problem with ample quantities of main memory? How would you solve it if you could use several external “scratch” files but only a few hundred bytes of main memory?

B. Rotate a one-dimensional vector of n elements left by i positions. For instance, with n=8 and i=3, the vector abcdefgh is rotated to defghabc. Simple code uses an n-element intermediate vector to do the job in n steps. Can you rotate the vector in time proportional to n using only a few dozen extra bytes of storage?

C. Given a dictionary of English words, find all sets of anagrams. For instance, “pots”, “stop” and “tops” are all anagrams of one another because each can be formed by permuting the letters of the others.

This example illustrates a technique that solves a multitude of programming problems: binary search. We initially know that an object is within a given range, and a probe operation tells us whether the object is below, at, or above a given position. Binary search locates the object by repeatedly probing the middle of the current range. If the probe doesn’t find the object, then we halve the current range and continue. We stop when we find what we’re looking for or when the range becomes empty.

The most common application of binary search in programming is to search for an element in a sorted array. When looking for the entry 50, the algorithm makes the following probes.

A binary search program is notoriously hard to get right; we’ll study the code in detail in Column 4.

Sequential search uses about n/2 comparisons on the average to search a table of n elements, while binary search never uses more than about log₂ n comparisons. That can make a big difference in system performance; this anecdote from a Communications of the ACM case study describing “The TWA Reservation System” is typical.

We had one program that was doing a linear search through a very large piece of memory almost 100 times a second. As the network grew, the average CPU time per message was up 0.3 milliseconds, which is a huge jump for us. We traced the problem to the linear search, changed the application program to use a binary search, and the problem went away.

I’ve seen that same story in many systems. Programmers start with the simple data structure of sequential search, which is often fast enough. If it becomes too slow, sorting the table and using a binary search can usually remove the bottleneck.

But the story of binary search doesn’t end with rapidly searching sorted arrays. Roy Weil applied the technique in cleaning an input file of about a thousand lines that contained a single bad line. Unfortunately, the bad line wasn’t known by sight; it could be identified only by running a (starting) portion of the file through a program and seeing a wildly erroneous answer, which took several minutes. His predecessors at debugging had tried to spot it by running a few lines at a time through the program, and they had been making progress towards a solution at a snail’s pace. How did Weil find the culprit in just ten runs of the program?

With this warmup, we can tackle Problem A. The input is on a sequential file (think of a tape or disk — although a disk may be randomly accessed, it is usually much faster to read a file from beginning to end). The file contains at most four billion 32-bit integers in random order, and we are to find one 32-bit integer not present. (There must be at least one missing, because there are 2³² or 4,294,967,296 such integers.) With ample main memory, we could use the bitmap technique from Column 1 and dedicate 536,870,912 8-bit bytes to a bitmap representing the integers seen so far. The problem, however, also asks how we can find the missing integer if we have only a few hundred bytes of main memory and several spare sequential files. To set this up as a binary search we have to define a range, a representation for the elements within the range, and a probing method to determine which half of a range holds the missing integer. How can we do this?

We’ll use as the range a sequence of integers known to contain at least one missing element, and we’ll represent the range by a file containing all the integers in it. The insight is that we can probe a range by counting the elements above and below its midpoint: either the upper or the lower range has at most half the elements in the total range. Because the total range has a missing element, the smaller half must also have a missing element. These are most of the ingredients of a binary search algorithm for the problem; try putting them together yourself before you peek at the solutions to see how Ed Reingold did it.

These uses of binary search just scratch the surface of its applications in programming. A root finder uses binary search to solve a single-variable equation by successively halving an interval; numerical analysts call this the bisection method. When the selection algorithm in Solution 11.9 partitions around a random element and then calls itself recursively on all elements on one side of that element, it is using a “randomized” binary search. Other uses of binary search include tree data structures and program debugging (when a program dies a silent death, where do you probe the source text to home in on the guilty statement?). In each of these examples, thinking of the program as a few embellishments on top of the basic binary search algorithm can give the programmer that all-powerful aha!

One might try to solve the problem by copying the first i elements of x to a temporary array, moving the remaining n – i elements left i places, and then copying the first i from the temporary array back to the last positions in x. However, the i extra locations used by this scheme make it too space-expensive. For a different approach, we could define a function to rotate x left one position (in time proportional to n) and call it i times, but that would be too time-expensive.

To solve the problem within the resource bounds will apparently require a more complicated program. One successful approach is a delicate juggling act: move x[0] to the temporary t, then move x[i] to x[0], x[2i] to x[i], and so on (taking all indices into x modulo n), until we come back to taking an element from x[0], at which point we instead take the element from t and stop the process. When i is 3 and n is 12, that phase moves the elements in this order.

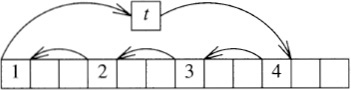
If that process didn’t move all the elements, then we start over at x[1], and continue until we move all the elements. Problem 3 challenges you to reduce this idea to code; be careful.

A different algorithm results from a different view of the problem: rotating the vector x is really just swapping the two segments of the vector ab to be the vector ba, where a represents the first i elements of x. Suppose a is shorter than b. Divide b into b_l and b_r so that b_r is the same length as a. Swap a and b_r to transform ab_lb_r into b_rb_la. The sequence a is in its final place, so we can focus on swapping the two parts of b. Since this new problem has the same form as the original, we can solve it recursively. This algorithm can lead to an elegant program (Solution 3 describes an iterative solution due to Gries and Mills), but it requires delicate code and some thought to see that it is efficient enough.

The problem looks hard until you finally have the aha! insight: let’s view the problem as transforming the array ab into the array ba, but let’s also assume that we have a function that reverses the elements in a specified portion of the array. Starting with ab, we reverse a to get a^rb, reverse b to get a^rb^r, and then reverse the whole thing to get (a^rb^r)^r, which is exactly ba. This results in the following code for rotation; the comments show the results when abcdefgh is rotated left three elements.

Click here to view code image

reverse(0, i-1)       /* cbadefgh */
reverse(i, n-1)       /* cbahgfed */
reverse(0, n-1)       /* defghabc */

Doug McIlroy gave this hand-waving example of rotating a ten-element array up five positions; start with your palms towards you, left over right.

The reversal code is time- and space-efficient, and is so short and simple that it’s pretty hard to get wrong. Brian Kernighan and P. J. Plauger used precisely this code in their 1981 Software Tools in Pascal to move lines within a text editor. Kernighan reports that it ran correctly the first time it was executed, while their previous code for a similar task based on linked lists contained several bugs. This code is used in several text processing systems, including the text editor with which I originally typed this column. Ken Thompson wrote the editor and the reversal code in 1971, and claims that it was part of the folklore even then.

Many approaches to this problem are surprisingly ineffective and complicated. Any method that considers all permutations of letters for a word is doomed to failure. The word “cholecystoduodenostomy” (an anagram in my dictionary of “duodenocholecystostomy”) has 22! permutations, and a few multiplications showed that 22! ≈ 1.124×10²¹. Even assuming the blazing speed of one picosecond per permutation, this will take 1.1×10⁹ seconds. The rule of thumb that “π seconds is a nanocentury” (see Section 7.1) tells us that 1.1×10⁹ seconds is a few decades. And any method that compares all pairs of words is doomed to at least an overnight run on my machine — there are about 230,000 words in the dictionary I used, and even a simple anagram comparison takes at least a microsecond, so the total time is roughly

230,000 words × 230,000 comparisons/word × 1 microsecond/comparison

= 52,900×10⁶ microseconds = 52,900 seconds ≈ 14.7 hours

Can you find a way to avoid both the above pitfalls?

The aha! insight is to sign each word in the dictionary so that words in the same anagram class have the same signature, and then bring together words with equal signatures. This reduces the original anagram problem to two subproblems: selecting a signature and collecting words with the same signature. Think about these problems before reading further.

For the first problem we’ll use a signature based on sorting†: order the letters within the word alphabetically. The signature of “deposit” is “deiopst”, which is also the signature of “dopiest” and any other word in that class. To solve the second problem, we’ll sort the words in the order of their signatures. The best description I have heard of this algorithm is Tom Cargill’s hand waving: sort this way (with a horizontal wave of the hand) then that way (a vertical wave). Section 2.8 describes an implementation of this algorithm.

† This anagram algorithm has been independently discovered by many people, dating at least as far back as the mid-1960’s.

Binary Search. The algorithm for looking up an element in a sorted table is remarkably efficient and can be used in main memory or on disk; its only drawback is that the entire table must be known and sorted in advance. The strategy underlying this simple algorithm is used in many other applications.

Signatures. When an equivalence relation defines classes, it is helpful to define a signature such that every item in a class has the same signature and no other item does. Sorting the letters within a word yields one signature for an anagram class; other signatures are given by sorting and then representing duplicates by a count (so the signature of “mississippi” might be “i4m1p2s4”, or “i4mp2s4” if 1’s are deleted) or by keeping a 26-integer array telling how many times each letter occurs. Other applications of signatures include the Federal Bureau of Investigation’s method for indexing fingerprints and the Soundex heuristic for identifying names that sound alike but are spelled differently.

Knuth describes the Soundex method in Chapter 6 of his Sorting and Searching.

Problem Definition. Column 1 showed that determining what the user really wants to do is an essential part of programming. The theme of this column is the next step in problem definition: what primitives will we use to solve the problem? In each case the aha! insight defined a new basic operation to make the problem trivial.

A Problem Solver’s Perspective. Good programmers are a little bit lazy: they sit back and wait for an insight rather than rushing forward with their first idea. That must, of course, be balanced with the initiative to code at the proper time. The real skill, though, is knowing the proper time. That judgment comes only with the experience of solving problems and reflecting on their solutions.

2. Given a sequential file containing 4,300,000,000 32-bit integers, how can you find one that appears at least twice?

3. We skimmed two vector rotation algorithms that require subtle code; implement each as a program. How does the greatest common divisor of i and n appear in each program?

4. Several readers pointed out that while all three rotation algorithms require time proportional to n, the juggling algorithm is apparently twice as fast as the reversal algorithm: it stores and retrieves each element of the array just once, while the reversal algorithm does so twice. Experiment with the functions to compare their speeds on real machines; be especially sensitive to issues surrounding the locality of memory references.

5. Vector rotation functions change the vector ab to ba; how would you transform the vector abc to cba? (This models the problem of swapping nonadjacent blocks of memory.)

6. In the late 1970’s, Bell Labs deployed a “user-operated directory assistance” program that allowed employees to look up a number in a company telephone directory using a standard push-button telephone.

To find the number of the designer of the system, Mike Lesk, one pressed “LESK*M*” (that is, “5375*6*”) and the system spoke his number. Such services are now ubiquitous. One problem that arises in such systems is that different names may have the same push-button encoding; when this happens in Lesk’s system, it asks the user for more information. Given a large file of names, such as a standard metropolitan telephone directory, how would you locate these “false matches”? (When Lesk did this experiment on such telephone directories, he found that the incidence of false matches was just 0.2 percent.) How would you implement the function that is given a push-button encoding of a name and returns the set of possible matching names?

7. In the early 1960’s, Vic Vyssotsky worked with a programmer who had to transpose a 4000-by-4000 matrix stored on magnetic tape (each record had the same format in several dozen bytes). The original program his colleague suggested would have taken fifty hours to run; how did Vyssotsky reduce the run time to half an hour?

8. [J. Ullman] Given a set of n real numbers, a real number t, and an integer k, how quickly can you determine whether there exists a k-element subset of the set that sums to at most t?

9. Sequential search and binary search represent a tradeoff between search time and preprocessing time. How many binary searches need be performed in an n-element table to buy back the preprocessing time required to sort the table?

10. On the day a new researcher reported to work for Thomas Edison, Edison asked him to compute the volume of an empty light bulb shell. After several hours with calipers and calculus, the fresh hire returned with the answer of 150 cubic centimeters. In a few seconds, Edison computed and responded “closer to 155” — how did he do it?

I organized my anagram program as a three-stage “pipeline” in which the output file of one program is fed as the input file to the next. The first program signs the words, the second sorts the signed file, and the third squashes the words in an anagram class onto one line. Here’s the process on a six-word dictionary.

The output contains three anagram classes.

The following C sign program assumes that no word contains more than one hundred letters and that the input file contains only lower-case letters and newline characters. (I therefore preprocessed the dictionary with a one-line command to change upper-case characters to lower case.)

Click here to view code image

int charcomp(char *x, char *y) { return *x - *y; }

#define WORDMAX 100
int main(void)
{   char word[WORDMAX], sig[WORDMAX];
    while (scanf("%s", word) != EOF) {
        strcpy(sig, word);
        qsort(sig, strlen(sig), sizeof(char), charcomp);
        printf("%s %s ", sig, word);
    }
    return 0;
}

The while loop reads one string at a time into word until it comes to the end of the file. The strcpy function copies the input word to the word sig, whose characters are then sorted by calling the C Standard Library qsort (the parameters are the array to be sorted, its length, the number of bytes per sort item, and the name of the function to compare two items, in this case, characters within the word). Finally, the printf statement prints the signature followed by the word itself and a newline.

The system sort program brings together all words with the same signature; the squash program prints them on a single line.

Click here to view code image

int main(void)
{   char word[WORDMAX], sig[WORDMAX], oldsig[WORDMAX];
    int linenum = 0;
    strcpy(oldsig, "");
    while (scanf("%s %s", sig, word) != EOF) {
        if (strcmp(oldsig, sig) != 0 && linenum > 0)
            printf(" ");
        strcpy(oldsig, sig);
        linenum++;
        printf("%s ", word);
    }
    printf(" ");
    return 0;
}

The bulk of the work is performed by the second printf statement; for each input line, it writes out the second field followed by a space. The if statement catches the changes between signatures: if sig changes from oldsig (its previous value), then a newline is printed (as long as this record isn’t the first in the file). The last printf writes a final newline character.

After testing those simple parts on small input files, I constructed the anagram list by typing

Click here to view code image

sign <dictionary | sort | squash >gramlist

That command feeds the file dictionary to the program sign, pipes sign’s output into sort, pipes sort’s output into squash, and writes squash’s output in the file gramlist. The program ran in 18 seconds: 4 in sign, 11 in sort and 3 in squash.

I ran the program on a dictionary that contains 230,000 words; it does not, however, include many -s and -ed endings. The following were among the more interesting anagram classes.

Click here to view code image

subessential suitableness
canter creant Cretan nectar recant tanrec trance
caret carte cater crate creat creta react recta trace
destain instead sainted satined
adroitly dilatory idolatry
least setal slate stale steal stela tales
reins resin rinse risen serin siren
constitutionalism misconstitutional