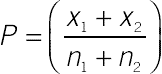When the same users are used in each group the test design is within-subjects (also called matched pairs). As with the continuous within-subjects test (the paired t-test) the variation between users has been removed and you have a better chance of detecting differences (higher power) with the same sample size as a between-subjects design.
To determine whether there is a significant difference between completion rates, conversion rates, or any dichotomous variable we use the McNemar exact test and generate p-values by testing whether the proportion of discordant pairs is greater than 0.5 (called the sign test) for all sample sizes.
McNemar exact test
The McNemar exact test uses a 2 × 2 table similar to those in the between-subjects section, but the primary test metric is the number of participants who switch from pass to fail or fail to pass—the discordant pairs (
McNemar, 1969).
Unlike the between-subjects chi-square test, we cannot setup our 2 × 2 table just from the summary data of the participants who passed and failed. We need to know the number who had a different outcome on each design—the discordant pairs of responses.
Table 5.9 shows the nomenclature used to represent the cells of the 2 × 2 table for this type of analysis.
Table 5.9
Nomenclature for McNemar Exact Test
|
Design B Pass |
Design B Fail |
Total |
| Design A |
a
|
b
|
m
|
| Design B |
c
|
d
|
n
|
| Total |
r
|
s
|
N
|
We want to know if the proportion of discordant pairs (cells b and c) is greater than what we’d expect to see from chance alone. For this type of analysis, we set chance to 0.50. If the proportion of pairs that are discordant is different from 0.50 (higher or lower), then we have evidence that there is a difference between designs.
To test the observed proportion against a test proportion, we use the nonparametric binomial test. This is the same approach we took in
Chapter 4 (Comparing Small Sample Completion Rates to a Criterion). When the proportion tested is 0.50, the binomial test goes by the special name “the sign test.”
The sign test uses the following binomial probability formula:
p(x)=n!x!(n−x)!px(1−p)(n−x)
where
x is the number of positive or negative discordant pairs (cell c or cell b, whichever is smaller),
n is the total number of discordant pairs (cell b + cell c), and
p = .50.
Note: The term
n! is pronounced “
n factorial” and is
n×(n−1)×(n−2)×⋯× 2×1
.
As discussed in
Chapter 4, we will again use mid-probabilities as a less conservative alternative to exact probabilities, which tend to overstate the value of
p, especially when sample sizes are small.
Example 1: Completion rates
For example, 15 users attempted the same task on two different designs. The completion rate on Design A was 87% and on Design B was 53%.
Table 5.10 shows how each user performed, with 0s representing failed task attempts and 1s for passing attempts.
Table 5.10
Sample Data for McNemar Exact Test
| User |
Design A |
Design B |
| 1 |
1 |
0 |
| 2 |
1 |
1 |
| 3 |
1 |
1 |
| 4 |
1 |
0 |
| 5 |
1 |
0 |
| 6 |
1 |
1 |
| 7 |
1 |
1 |
| 8 |
0 |
1 |
| 9 |
1 |
0 |
| 10 |
1 |
1 |
| 11 |
0 |
0 |
| 12 |
1 |
1 |
| 13 |
1 |
0 |
| 14 |
1 |
1 |
| 15 |
1 |
0 |
| Comp rate |
87% |
53% |
Next we total the number of concordant and discordant responses in a 2 × 2 table (
Table 5.11).
Table 5.11
Concordant and Discordant Responses for Example 1
|
Design B Pass |
Design B Fail |
Total |
| Design A Pass |
7 (a) |
6 (b) |
13 (m) |
| Design A Fail |
1 (c) |
1 (d) |
2 (n) |
| Total |
8 (r) |
7 (s) |
15 (N) |
Concordant pairs
• Seven users completed the task on both designs (cell a)
• One user failed on Design A and failed on Design B (cell d)
Discordant pairs
• Six users completed on Design A but failed on Design B (cell b)
• One user failed on Design A and passed on Design B (cell c)
Table 5.12 shows the discordant users along with a sign (positive or negative) to indicate whether they performed better (plus sign) or worse (negative sign) on Design B. By the way, this is where this procedure gets its name the “sign test”—we’re testing whether the proportion of pluses to minuses is significantly different from 0.50.
Table 5.12
Discordant Performance from Example 1
| User |
Relative Performance on B |
| 1 |
− |
| 4 |
− |
| 5 |
− |
| 8 |
+ |
| 9 |
− |
| 13 |
− |
| 15 |
− |
In total, there were seven discordant pairs (cell b + cell c). Most users who performed differently performed better on Design A (six of seven). We will use the smaller of the discordant cells to simplify the computation, which is the one person in cell c who failed on Design A and passed on Design B. (Note that you will get the same result if you used the larger of the discordant cells, but it would be more work.) Plugging these values in the formula, we get
p(0)=7!0!(7−0)!0.50(1−0.5)(7−0)=0.0078
p(1)=7!1!(7−1)!0.51(1−0.5)(7−1)=0.0547
The one-tailed exact-p value is these two probabilities added together, 0.0078 + 0.0547 = 0.0625, so the two-tailed probability is double this (0.125). The mid-probability is equal to half the exact probability for the value observed plus the cumulative probability of all values less than the one observed. In this case, the probability of all values less than the one observed is just the probability of 0 discordant pairs, which is 0.0078:
Mid p=120.0547+0.0078
Mid p=0.0352
The one-tailed mid-p value is 0.0352, so the two-tailed mid-p value is double this (0.0704). Thus, the probability of seeing one out of seven users perform better on Design A than B if there really was no difference is 0.0704. Put another way, we can be about 93% sure Design A has a better completion rate than Design B.
The computations for this two-sided mid-p value are rather tedious to do by hand, but are fairly easy to get using the Excel function =2*(BINOMDIST(0,7,0.5,FALSE) + 0.5*BINOMDIST(1,7,0.5,FALSE)).
If you need to guarantee that the reported
p-value is greater than or equal to the actual long-term probability, then you should use the exact-
p values instead of the mid-
p values. This is similar to the recommendation we gave when comparing the completion rate to a benchmark and when computing binomial confidence intervals (see
Chapter 4). For most applications in user research, the mid-
p value will work better (lead to more correct decisions) over the long run (
Agresti and Coull, 1998).
Alternate approaches
As with the between-subjects chi-square test, there isn’t much agreement among statistics texts (or statisticians) on the best way to compute the within-subjects p-value. This section provides information about additional approaches you might have encountered. You may safely skip this section if you trust our recommendation (or if you’re not interested in more geeky technical details).
Chi-square statistic
The most common recommendation in statistics text books for large sample within-subject comparisons is to use the chi-square statistic. It is typically called the McNemar chi-square test (
McNemar, 1969), as opposed to the McNemar exact test which we presented in the earlier section. It uses the following formula:
χ2=(c−b)2c+b
You will notice that the formula only uses the discordant cells (b and c). You can look up the test statistic in a chi-square table with 1 degree of freedom to generate the p-value, or use the Excel CHIDIST function. Using the data from Example 1 with seven discordant pairs we get a test statistic of
χ2=(1−6)27=3.571
Using the Excel function =CHIDIST(3.571, 1), we get the p-value of 0.0587, which, for this example, is reasonably close to our mid-p value of 0.0704.
However, to use this approach, the sample size needs to be reasonably large to have accurate results. As a general guide, it is a large enough sample if the number of discordant pairs (
b +
c) is greater than 30 (
Agresti and Franklin, 2007).
You can equivalently use the z-statistic and corresponding normal table of values to generate a p-value instead of the chi-square statistic, by simply taking the square root of the entire equation.
Z=c−bc+b√
Z=6−16+1√=57√=1.89
Using the Excel NORMSDIST function (=2*NORMSDIST(1.89)), we get p = 0.0587, demonstrating the mathematical equivalence of the methods.
Yates correction to the chi-square statistic
To further complicate matters, some texts recommend using a Yates corrected chi-square for all sample sizes (
Bland, 2000). As shown in the following, the Yates correction is
χ2=(|c−b|−1)2b+c
Using the data from Example 1 with seven discordant pairs we get
χ2=(|1−6|−1)27=2.29
We look up this value in a chi-square table of values with 1 degree of freedom or use the Excel function =CHIDIST(2.29, 1) to get the p-value of 0.1306. For this example, this value is even higher than the exact-p value from the sign test, which we expect to overstate the magnitude of p. A major criticism of the Yates correction is that it will likely exceed the p-value from the sign test. Recall that this overcorrection also occurs with the Yates correction of the between-subjects chi-square test. For this reason, we do not recommend the use of the Yates correction.
Table 5.13 provides a summary of the
p-values generated from the different approaches and our recommendations.
Table 5.13
Summary of p-values Generated from Sample Data for McNemar Tests
| Method |
P-value |
Notes |
| McNemar exact test using mid-probabilities |
0.0704 |
Recommended: For all sample sizes will provide best average long-term probability, but some individual tests may understate actual probability |
| McNemar exact test using exact probabilities |
0.125 |
Recommended: For all sample sizes when you need to guarantee the long-term probability is greater than or equal to the p-value (a conservative approach) |
| McNemar chi-square test/z
test |
0.0587 |
Not Recommended: Understates true probability for sample sizes and is unclear about what constitutes a large sample size |
| McNemar chi-square test with Yates correction |
0.1306 |
Not Recommended: Overstates true probability for all sample sizes |
Confidence interval around the difference for matched pairs
To estimate the likely magnitude of the difference between matched pairs of binary responses, we recommend the appropriate adjusted-Wald confidence interval (
Agresti and Min, 2005). As described in
Chapter 3 for confidence intervals around a single proportion, this adjustment uses the same concept as that for the between-subjects confidence interval around two proportions.
When applied to a 2 × 2 table for a within-subjects setup (as shown in
Table 5.14),
the adjustment is to add 1/8
th of a squared critical value from the normal distribution for the specified level of confidence
to each cell in the 2 × 2 table. For a 95% level of confidence, this has the effect of adding two pseudo observations to the total number of trials (
N).
Table 5.14
Framework for Adjusted-Wald Confidence Interval
|
Design B Pass |
Design B Fail |
Total |
| Design A Pass |
aadj
|
badj
|
madj
|
| Design A Fail |
cadj
|
dadj
|
nadj
|
| Total |
radj
|
sadj
|
Nadj
|
Using the same notation from the 2 × 2 table with the “adj” meaning to add
z2α8
to each value, we have the formula:
(pˆ2adj−pˆ1adj)±zα(pˆ12adj+pˆ21adj)−(pˆ21adj−pˆ12adj)2Nadj−−−−−−−−−−−−−−−−−−√
where
pˆ1adj=madjNadj
pˆ2adj=radjNadj
pˆ12adj=badjNadj
pˆ21adj=cadjNadj
zα = two-sided z critical value for the level of confidence (e.g., 1.96 for a 95% confidence level)
z2α8
= The adjustment added to each cell (e.g., for a 95% confidence level this is
1.9628=0.48
)
The formula is similar to the confidence interval around two independent proportions. The key difference here is how we generate the proportions from the 2 × 2 table.
Table 5.15 shows the results from Example 1 (so you don’t need to flip back to the original page).
Table 5.15
Results from Example 1
|
Design B Pass |
Design B Fail |
Total |
| Design A Pass |
7 (a) |
6 (b) |
13 (m) |
| Design A Fail |
1 (c) |
1 (d) |
2 (n) |
| Total |
8 (r) |
7 (s) |
15 (N) |
Table 5.16 shows the adjustment of 0.5 added to each cell.
Table 5.16
Adjusted Values for Computing Confidence Interval
|
Design B Pass |
Design B Fail |
Total |
| Design A Pass |
7.5 (aadj) |
6.5 (badj) |
14 (madj) |
| Design A Fail |
1.5 (cadj) |
1.5 (dadj) |
3 (nadj) |
| Total |
9 (radj) |
8 (sadj) |
17 (Nadj) |
You can see that the adjustment has the effect of adding two pseudo users to the sample as we go from a total of 15–17. Filling these values in the formula for a 95% confidence interval (which has a critical z-value of 1.96) we get
pˆ1adj=1417=0.825
pˆ2adj=917=0.529
pˆ12adj=6.517=0.383
pˆ21adj=1.517=0.087
(pˆ2adj−pˆ1adj)±zα(pˆ12adj+pˆ21adj)−(pˆ21adj−pˆ12adj)2Nadj−−−−−−−−−−−−−−−−−−√
(0.529−0.825)±1.96(0.383+0.087)−(0.087−0.383)217−−−−−−−−−−−−−−−−−−√
−0.296±0.295
The 95% confidence interval around the difference in completion rates between designs is −59.1% to −0.1%. The confidence interval goes from negative to positive because we subtracted the design with the better completion rate from the one with the worse completion rate.
There’s nothing sacred about the order in which you subtract the proportions. We can just as easily subtract Design B from Design A, which would generate a confidence interval of 0.1– 59.1%. Neither confidence interval quite crosses 0, so we can be about 95% confident there is a difference. It is typically easier to subtract the smaller proportion from the larger when reporting confidence intervals, so we will do that through the remainder of this section.
The mid-p value from the McNemar exact test was 0.0704 which gave us around 93% confidence that there was a difference—just short of the 95% confidence indicated by the adjusted-Wald confidence interval (which is based on a somewhat different statistical procedure), but likely confident enough for many early stage designs to move on to the next research question (or make any indicated improvements to the current design and move on to testing the next design).
In most applied settings, the difference between 94% confidence and 95% confidence shouldn’t lead to different decisions. If you are using a rigid cutoff of 0.05, such as for a publication, then use the
p-value to decide whether to reject the null hypothesis. Keep in mind that most statistical calculations approximate the role of chance. Both the approximation and the choice of the method used can result in
p-values that fluctuate by a few percentage points (as we saw in
Table 5.13) so don’t get too hung up on what the “right”
p-value is. If you are testing in an environment where you need to guarantee a certain
p-value (medical device testing come to mind), then increasing your confidence level to 99% and using the exact-
p values instead of the mid-
p values will significantly reduce the probability of identifying a chance difference as significant.
Example 2: Completion rates
In a comparative usability test, 14 users attempted to rent the same type of car in the same city on two different websites (
Avis.com and
Enterprise.com). All 14 users completed the task on
Avis.com but only 10 of 14 completed it on
Enterprise.com. The users and their task results appear in
Table 5.17 and
Table 5.18.
Is there sufficient evidence that more users could complete the task on
Avis.com than on
Enterprise.com (as designed at the time of this study)?
Table 5.17
Completion Data from CUE-8 Task
| User |
Avis.com
|
Enterprise.com
|
| 1 |
1 |
1 |
| 2 |
1 |
1 |
| 3 |
1 |
0 |
| 4 |
1 |
0 |
| 5 |
1 |
1 |
| 6 |
1 |
1 |
| 7 |
1 |
1 |
| 8 |
1 |
0 |
| 9 |
1 |
1 |
| 10 |
1 |
1 |
| 11 |
1 |
1 |
| 12 |
1 |
0 |
| 13 |
1 |
1 |
| 14 |
1 |
1 |
| Comp rate |
100% |
71% |
Table 5.18
Organization of Concordant and Discordant Pairs from CUE-8 Task
In total there were four discordant users (cell
b + cell
c), all of which performed better on
Avis.com.
Table 5.19 shows the improvement performance difference for the four users on
Enterprise.com.
Table 5.19
Discordant Performance from CUE-8 Task
| User |
Relative Performance on Enterprise.com
|
| 3 |
— |
| 4 |
— |
| 8 |
— |
| 12 |
— |
Plugging the appropriate values in the formula we get
p(x)=n!x!(n−x)!px(1−p)(n−x)
p(0)=4!0!(4−0)!0.50(1−0.5)(4−0)=0.0625
The one-tailed exact-p value is 0.0625, so the two-tailed probability is double this (0.125). The mid-probability is equal to half the exact probability for the value observed plus the cumulative probability of all values less than the one observed. Because there are no values less than 0, the one-tailed mid-probability is equal to half of 0.0625:
Mid -p=12(0.0625)
Mid- p=0.0313
The one-tailed mid-
p value is 0.0313, so the two-tailed mid-
p value is double this (0.0625). Thus, the probability of seeing zero out of four users perform worse on
Enterprise.com if there really was no difference is 0.0625. Put another way, we can be around 94% sure
Avis.com had a better completion rate than
Enterprise.com on this rental car task at the time of this study.
Comparing rental car websites
Why Enterprise.com had a worse completion rate— from the files of Jeff Sauro
In case you were wondering why
Enterprise.com had a worse completion rate, the task required users to add a GPS system to the rental car reservation. On
Enterprise.com, this option only appeared AFTER you entered your personal information. It thus led four users to spend a lot of time hunting for that option and either giving up or saying they would call customer service. Allowing users to add that feature (which changes the total rental price) would likely increase the completion rate (and rental rate) for
Enterprise.com.
The 95% confidence interval around the difference is found by first adjusting the values in each interior cell of the 2 × 2 table by 0.5
(1.9628=0.48≈0.5)
, as shown in
Table 5.20.
Table 5.20
Adjusted Counts for CUE-8 Task
|
Design B Pass |
Design B Pass |
Total |
| Design A Pass |
10.5 (aadj) |
4.5 (badj) |
15 (madj) |
| Design A Fail |
0.5 (cadj) |
0.5 (dadj) |
1 (nadj) |
| Total |
11 (radj) |
5 (sadj) |
16 (Nadj) |
Finding the component parts of the formula and entering the values we get
(pˆ2adj−pˆ1adj)±zα(pˆ12adj+pˆ21adj)−(pˆ21adj−pˆ12adj)2Nadj−−−−−−−−−−−−−−−−−−√
pˆ1adj=madjNadj=1516=0.938
pˆ2adj=radjNadj=1116=0.688
pˆ12adj=badjNadj=4.516=0.281
pˆ21adj=cadjNadj=0.516=0.03
(0.938−0.688)±1.96(0.281+0.03)−(0.03−0.281)216−−−−−−−−−−−−−−−−−√
0.250±0.245
We can be 95% confident the difference between proportions is between 0.5% and 49.5%. This interval does not cross zero which tells us we can be 95% confident the difference is greater than zero. It is another example of a significant difference seen with the confidence interval but not with the p-value. We didn’t plan on both examples having p-values so close to 0.05. They are a consequence of using data from actual usability tests. Fortunately, you are more likely to see p-values and confidence intervals point to the same conclusion.


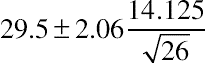
 which is based on a table of values that is one-sided. We find this approach more confusing because in most cases you’ll be working with two-sided rather than one-sided confidence intervals. It is also inconsistent with the Excel TINV function, which is a very convenient way to get desired values of t when computing confidence intervals.
which is based on a table of values that is one-sided. We find this approach more confusing because in most cases you’ll be working with two-sided rather than one-sided confidence intervals. It is also inconsistent with the Excel TINV function, which is a very convenient way to get desired values of t when computing confidence intervals.

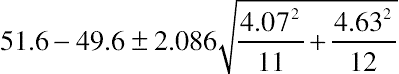

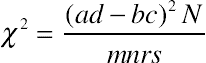



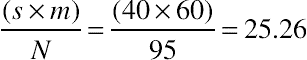
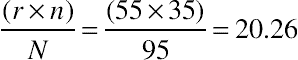














 . This adjustment is algebraically equivalent to the N−1 chi-square adjustment. The resulting formula is
. This adjustment is algebraically equivalent to the N−1 chi-square adjustment. The resulting formula is
 , where x1 and x2 are the numbers completing or converting, and n1 and n2 are the numbers attempting
, where x1 and x2 are the numbers completing or converting, and n1 and n2 are the numbers attempting











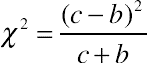

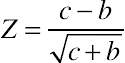









 )
)



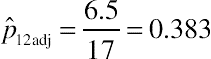



 , as shown in Table 5.20.
, as shown in Table 5.20.