What sample sizes do we need? Part 2: formative studies
Abstract
The purpose of formative user research is to discover and enumerate the events of interest in the study (e.g., the problems that participants experience during a formative usability study). The statistical methods used to estimate sample sizes for formative research draw upon techniques not routinely taught in introductory statistics classes. This chapter covers techniques based on the binomial probability model and discusses issues associated with violation of the assumptions of the binomial model when averaging probabilities across a set of problems or participants while maintaining a focus on practical aspects of iterative design.
Keywords
Introduction
Using a probabilistic model of problem discovery to estimate sample sizes for formative user research
The famous equation P(x ≥ 1) = 1 – (1 – p)n

Deriving a sample size estimation equation from 1 – (1 – p)n



Table 7.1
Sample Size Requirements for Formative User Research
| p | P(x ≥ 1) = 0.50 | P(x ≥ 1) = 0.75 | P(x ≥ 1) = 0.85 | P(x ≥ 1) = 0.90 | P(x ≥ 1) = 0.95 | P(x ≥ 1) = 0.99 |
| 0.01 | 69 (168) | 138 (269) | 189 (337) | 230 (388) | 299 (473) | 459 (662) |
| 0.05 | 14 (34) | 28 (53) | 37 (67) | 45 (77) | 59 (93) | 90 (130) |
| 0.10 | 7 (17) | 14 (27) | 19 (33) | 22 (38) | 29 (46) | 44 (64) |
| 0.15 | 5 (11) | 9 (18) | 12 (22) | 15 (25) | 19 (30) | 29 (42) |
| 0.25 | 3 (7) | 5 (10) | 7 (13) | 9 (15) | 11 (18) | 17 (24) |
| 0.50 | 1 (3) | 2 (5) | 3 (6) | 4 (7) | 5 (8) | 7 (11) |
| 0.90 | 1 (2) | 1 (2) | 1 (3) | 1 (3) | 2 (3) | 2 (4) |

Note: The first number in each cell is the sample size required to detect the event of interest at least once; numbers in parentheses are the sample sizes required to observe the event of interest at least twice
Table 7.2
Likelihood of Discovery for Various Sample Sizes
| p | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
| 0.01 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 |
| 0.05 | 0.05 | 0.10 | 0.14 | 0.19 | 0.23 |
| 0.10 | 0.10 | 0.19 | 0.27 | 0.34 | 0.41 |
| 0.15 | 0.15 | 0.28 | 0.39 | 0.48 | 0.56 |
| 0.25 | 0.25 | 0.44 | 0.58 | 0.68 | 0.76 |
| 0.50 | 0.50 | 0.75 | 0.88 | 0.94 | 0.97 |
| 0.90 | 0.90 | 0.99 | 1.00 | 1.00 | 1.00 |
| p | n = 6 | n = 7 | n = 8 | n = 9 | n = 10 |
| 0.01 | 0.06 | 0.07 | 0.08 | 0.09 | 0.10 |
| 0.05 | 0.26 | 0.30 | 0.34 | 0.37 | 0.40 |
| 0.10 | 0.47 | 0.52 | 0.57 | 0.61 | 0.65 |
| 0.15 | 0.62 | 0.68 | 0.73 | 0.77 | 0.80 |
| 0.25 | 0.82 | 0.87 | 0.90 | 0.92 | 0.94 |
| 0.50 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 |
| 0.90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| p | n = 11 | n = 12 | n = 13 | n = 14 | n = 15 |
| 0.01 | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 |
| 0.05 | 0.43 | 0.46 | 0.49 | 0.51 | 0.54 |
| 0.10 | 0.69 | 0.72 | 0.75 | 0.77 | 0.79 |
| 0.15 | 0.83 | 0.86 | 0.88 | 0.90 | 0.91 |
| 0.25 | 0.96 | 0.97 | 0.98 | 0.98 | 0.99 |
| 0.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| p | n = 16 | n = 17 | n = 18 | n = 19 | n = 20 |
| 0.01 | 0.15 | 0.16 | 0.17 | 0.17 | 0.18 |
| 0.05 | 0.56 | 0.58 | 0.60 | 0.62 | 0.64 |
| 0.10 | 0.81 | 0.83 | 0.85 | 0.86 | 0.88 |
| 0.15 | 0.93 | 0.94 | 0.95 | 0.95 | 0.96 |
| 0.25 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 |
| 0.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |

Using the tables to plan sample sizes for formative user research

Assumptions of the binomial probability model
Additional applications of the model
Estimating the composite value of p for multiple problems or other events
Table 7.3
Hypothetical Results for a Formative Usability Study
| Problem | ||||||||||||
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Count | Proportion |
| 1 | x | x | x | x | x | x | 6 | 0.6 | ||||
| 2 | x | x | x | x | x | 5 | 0.5 | |||||
| 3 | x | x | x | x | x | 5 | 0.5 | |||||
| 4 | x | x | x | x | 4 | 0.4 | ||||||
| 5 | x | x | x | x | x | x | 6 | 0.6 | ||||
| 6 | x | x | x | x | 4 | 0.4 | ||||||
| 7 | x | x | x | x | 4 | 0.4 | ||||||
| 8 | x | x | x | x | x | 5 | 0.5 | |||||
| 9 | x | x | x | x | x | 5 | 0.5 | |||||
| 10 | x | x | x | x | x | x | 6 | 0.6 | ||||
| Count | 10 | 8 | 6 | 5 | 5 | 4 | 5 | 3 | 3 | 1 | 50 | |
| Proportion | 1.0 | 0.8 | 0.6 | 0.5 | 0.5 | 0.4 | 0.5 | 0.3 | 0.3 | 0.1 | 0.50 | |

Note: x = specified participant experienced specified problem.
Adjusting small-sample composite estimates of p

Table 7.4
Hypothetical Results for a Formative Usability Study: First Four Participants and all Problems
| Problem | ||||||||||||
| Participant | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Count | Proportion |
| 1 | x | x | x | x | x | x | 6 | 0.75 | ||||
| 2 | x | x | x | x | x | 5 | 0.625 | |||||
| 3 | x | x | x | x | x | 5 | 0.625 | |||||
| 4 | x | x | x | x | 4 | 0.5 | ||||||
| Count | 4 | 4 | 0 | 4 | 1 | 3 | 2 | 2 | 0 | 0 | 20 | |
| Proportion | 1.0 | 1.0 | 0 | 1.0 | 0.25 | 0.75 | 0.5 | 0.5 | 0 | 0 | 0.50 | |

Note: x = specified participant experienced specified problem.
Table 7.5
Hypothetical Results for a Formative Usability Study: First Four Participants and Only Problems Observed with Those Participants
| Problem | |||||||||
| Participant | 1 | 2 | 4 | 5 | 6 | 7 | 8 | Count | Proportion |
| 1 | x | x | x | x | x | x | 6 | 0.86 | |
| 2 | x | x | x | x | x | 5 | 0.71 | ||
| 3 | x | x | x | x | x | 5 | 0.71 | ||
| 4 | x | x | x | x | 4 | 0.57 | |||
| Count | 4 | 4 | 4 | 1 | 3 | 2 | 2 | 20 | |
| Proportion | 1.0 | 1.0 | 1.0 | 0.25 | 0.75 | 0.5 | 0.5 | 0.71 | |

Note: x = specified participant experienced specified problem.








Estimating the number of problems available for discovery and the number of undiscovered problems

What affects the value of p?
What is a reasonable problem discovery goal?
Table 7.6
Variables and Results of the Lewis (1994) ROI Simulations
| Independent Variable | Value | Sample Size at Maximum ROI | Magnitude of Maximum ROI | Percentage of Problems Discovered at Maximum ROI |
| Average likelihood of problem discovery (p) | 0.10 | 19.0 | 3.1 | 86 |
| 0.25 | 14.6 | 22.7 | 97 | |
| 0.50 | 7.7 | 52.9 | 99 | |
| Range: | 11.3 | 49.8 | 13 | |
| Number of problems available for discovery | 30 | 11.5 | 7.0 | 91 |
| 150 | 14.4 | 26.0 | 95 | |
| 300 | 15.4 | 45.6 | 95 | |
| Range: | 3.9 | 38.6 | 4 | |
| Daily cost to run a study | 500 | 14.3 | 33.4 | 94 |
| 1000 | 13.2 | 19.0 | 93 | |
| Range: | 1.1 | 14.4 | 1 | |
| Cost to fix a discovered problem | 100 | 11.9 | 7.0 | 92 |
| 1000 | 15.6 | 45.4 | 96 | |
| Range: | 3.7 | 38.4 | 4 | |
| Cost of an undiscovered problem (low set) | 200 | 10.2 | 1.9 | 89 |
| 500 | 12.0 | 6.4 | 93 | |
| 1000 | 13.5 | 12.6 | 94 | |
| Range: | 3.3 | 10.7 | 5 | |
| Cost of an undiscovered problem (high set) | 2000 | 14.7 | 12.3 | 95 |
| 5000 | 15.7 | 41.7 | 96 | |
| 10000 | 16.4 | 82.3 | 96 | |
| Range: | 1.7 | 70.0 | 1 |

Reconciling the “Magic Number Five” with “Eight is Not Enough”
Some history—the 1980s
Having collected data from a few test subjects – and initially a few are all you need – you are ready for a revision of the text. Revisions may involve nothing more than changing a word or a punctuation mark. On the other hand, they may require the insertion of new examples and the rewriting, or reformatting, of an entire frame. This cycle of test, evaluate, rewrite is repeated as often as is necessary.
Some more history—the 1990s
The number of usability results found by aggregates of evaluators grows rapidly in the interval from one to five evaluators but reaches the point of diminishing returns around the point of ten evaluators. We recommend that heuristic evaluation is done with between three and five evaluators and that any additional resources are spent on alternative methods of evaluation (Nielsen and Molich, 1990, p. 255).
The basic findings are that (a) 80% of the usability problems are detected with four or five subjects, (b) additional subjects are less and less likely to reveal new information, and (c) the most severe usability problems are likely to have been detected in the first few subjects (Virzi, 1992, p. 457).
The benefits are much larger than the costs both for user testing and for heuristic evaluation. The highest ratio of benefits to costs is achieved for 3.2 test users and for 4.4 heuristic evaluators. These numbers can be taken as one rough estimate of the effort to be expended for usability evaluation for each version of a user interface subjected to iterative design (Nielsen and Landauer, 1993, p. 212).
Problem discovery shows diminishing returns as a function of sample size. Observing four to five participants will uncover about 80% of a product’s usability problems as long as the average likelihood of problem detection ranges between .32 and .42, as in Virzi. If the average likelihood of problem detection is lower, then a practitioner will need to observe more than five participants to discover 80% of the problems. Using behavioral categories for problem severity (or impact), these data showed no correlation between problem severity (impact) and rate of discovery (Lewis, 1994, p. 368).
The derivation of the “Magic Number 5”
The Magic Number 5: “All you need to do is watch five people to find 85% of a product’s usability problems.”
The curve [1 – (1 - .31)n] clearly shows that you need to test with at least 15 users to discover all the usability problems in the design. So why do I recommend testing with a much smaller number of users? The main reason is that it is better to distribute your budget for user testing across many small tests instead of blowing everything on a single, elaborate study. Let us say that you do have the funding to recruit 15 representative customers and have them test your design. Great. Spend this budget on three tests with 5 users each. You want to run multiple tests because the real goal of usability engineering is to improve the design and not just to document its weaknesses. After the first study with 5 users has found 85% of the usability problems, you will want to fix these problems in a redesign. After creating the new design, you need to test again.
Eight is not enough—a reconciliation
When we tested the site with 18 users, we identified 247 total obstacles-to-purchase. Contrary to our expectations, we saw new usability problems throughout the testing sessions. In fact, we saw more than five new obstacles for each user we tested. Equally important, we found many serious problems for the first time with some of our later users. What was even more surprising to us was that repeat usability problems did not increase as testing progressed. These findings clearly undermine the belief that five users will be enough to catch nearly 85 percent of the usability problems on a Web site. In our tests, we found only 35 percent of all usability problems after the first five users. We estimated over 600 total problems on this particular online music site. Based on this estimate, it would have taken us 90 tests to discover them all!
Table 7.7
Expected Problem Discovery When p = .029 and There are 600 Problems
| Sample Size | Percent Discovered (%) | Total Number Discovered | New Problems | Sample Size | Percent Discovered (%) | Total Number Discovered | New Problems |
| 1 | 2.9 | 17 | 17 | 36 | 65.3 | 392 | 6 |
| 2 | 5.7 | 34 | 17 | 37 | 66.3 | 398 | 6 |
| 3 | 8.5 | 51 | 17 | 38 | 67.3 | 404 | 6 |
| 4 | 11.1 | 67 | 16 | 39 | 68.3 | 410 | 6 |
| 5 | 13.7 | 82 | 15 | 40 | 69.2 | 415 | 5 |
| 6 | 16.2 | 97 | 15 | 41 | 70.1 | 420 | 5 |
| 7 | 18.6 | 112 | 15 | 42 | 70.9 | 426 | 6 |
| 8 | 21.0 | 126 | 14 | 43 | 71.8 | 431 | 5 |
| 9 | 23.3 | 140 | 14 | 44 | 72.6 | 436 | 5 |
| 10 | 25.5 | 153 | 13 | 45 | 73.4 | 440 | 4 |
| 11 | 27.7 | 166 | 13 | 46 | 74.2 | 445 | 5 |
| 12 | 29.8 | 179 | 13 | 47 | 74.9 | 450 | 5 |
| 13 | 31.8 | 191 | 12 | 48 | 75.6 | 454 | 4 |
| 14 | 33.8 | 203 | 12 | 49 | 76.4 | 458 | 4 |
| 15 | 35.7 | 214 | 11 | 50 | 77.0 | 462 | 4 |
| 16 | 37.6 | 225 | 11 | 51 | 77.7 | 466 | 4 |
| 17 | 39.4 | 236 | 11 | 52 | 78.4 | 470 | 4 |
| 18 | 41.1 | 247 | 11 | 53 | 79.0 | 474 | 4 |
| 19 | 42.8 | 257 | 10 | 54 | 79.6 | 478 | 4 |
| 20 | 44.5 | 267 | 10 | 55 | 80.2 | 481 | 3 |
| 21 | 46.1 | 277 | 10 | 56 | 80.8 | 485 | 4 |
| 22 | 47.7 | 286 | 9 | 57 | 81.3 | 488 | 3 |
| 23 | 49.2 | 295 | 9 | 58 | 81.9 | 491 | 3 |
| 24 | 50.7 | 304 | 9 | 59 | 82.4 | 494 | 3 |
| 25 | 52.1 | 313 | 9 | 60 | 82.9 | 497 | 3 |
| 26 | 53.5 | 321 | 8 | 61 | 83.4 | 500 | 3 |
| 27 | 54.8 | 329 | 8 | 62 | 83.9 | 503 | 3 |
| 28 | 56.1 | 337 | 8 | 63 | 84.3 | 506 | 3 |
| 29 | 57.4 | 344 | 7 | 64 | 84.8 | 509 | 3 |
| 30 | 58.6 | 352 | 8 | 65 | 85.2 | 511 | 2 |
| 31 | 59.8 | 359 | 7 | 66 | 85.7 | 514 | 3 |
| 32 | 61.0 | 366 | 7 | 67 | 86.1 | 516 | 2 |
| 33 | 62.1 | 373 | 7 | 68 | 86.5 | 519 | 3 |
| 34 | 63.2 | 379 | 6 | 69 | 86.9 | 521 | 2 |
| 35 | 64.3 | 386 | 7 | 70 | 87.3 | 524 | 3 |

There will, of course, continue to be discussions about sample sizes for problem-discovery usability tests, but I hope they will be informed discussions. If a practitioner says that five participants are all you need to discover most of the problems that will occur in a usability test, it’s likely that this practitioner is typically working in contexts that have a fairly high value of p and fairly low problem discovery goals. If another practitioner says that he’s been running a study for three months, has observed 50 participants, and is continuing to discover new problems every few participants, then it’s likely that he has a somewhat lower value of p, a higher problem discovery goal, and lots of cash (or a low-cost audience of participants). Neither practitioner is necessarily wrong – they’re just working in different usability testing spaces. The formulas developed over the past 25 years provide a principled way to understand the relationship between those spaces, and a better way for practitioners to routinely estimate sample-size requirements for these types of tests.
More about the binomial probability formula and its small-sample adjustment
The origin of the binomial probability formula









How does the deflation adjustment work?
Table 7.8
Two Extreme Patterns of Three Participants Encountering Problems
| Outcome A | Problems | ||||
| Participant | 1 | 2 | 3 | Count | Proportion |
| 1 | x | x | x | 3 | 1.00 |
| 2 | x | x | x | 3 | 1.00 |
| 3 | x | x | x | 3 | 1.00 |
| Count | 3 | 3 | 3 | 9 | |
| Proportion | 1.00 | 1.00 | 1.00 | 1.00 | |
| Outcome B | Problems | ||||
| Participant | 1 | 2 | 3 | Count | Proportion |
| 1 | x | 1 | 0.33 | ||
| 2 | x | 1 | 0.33 | ||
| 3 | x | 1 | 0.33 | ||
| Count | 1 | 1 | 1 | 3 | |
| Proportion | 0.33 | 0.33 | 0.33 | 0.33 | |

Other statistical models for problem discovery
Criticisms of the binomial model for problem discovery
Expanded binomial models
The beta-binomial distribution is a compound distribution of the beta and the binomial distributions. It is a natural extension of the binomial model. It is obtained with the parameter p in the binomial distribution is assumed to follow a beta distribution with parameters a and b. … It is convenient to reparameterize to μ = a/(a + b), θ = 1/(a + b) because parameters μ and θ are more meaningful. μ is the mean of the binomial parameter p. θ is a scale parameter which measures the variation of p.
Capture-recapture models
Why not use one of these other models when planning formative user research?
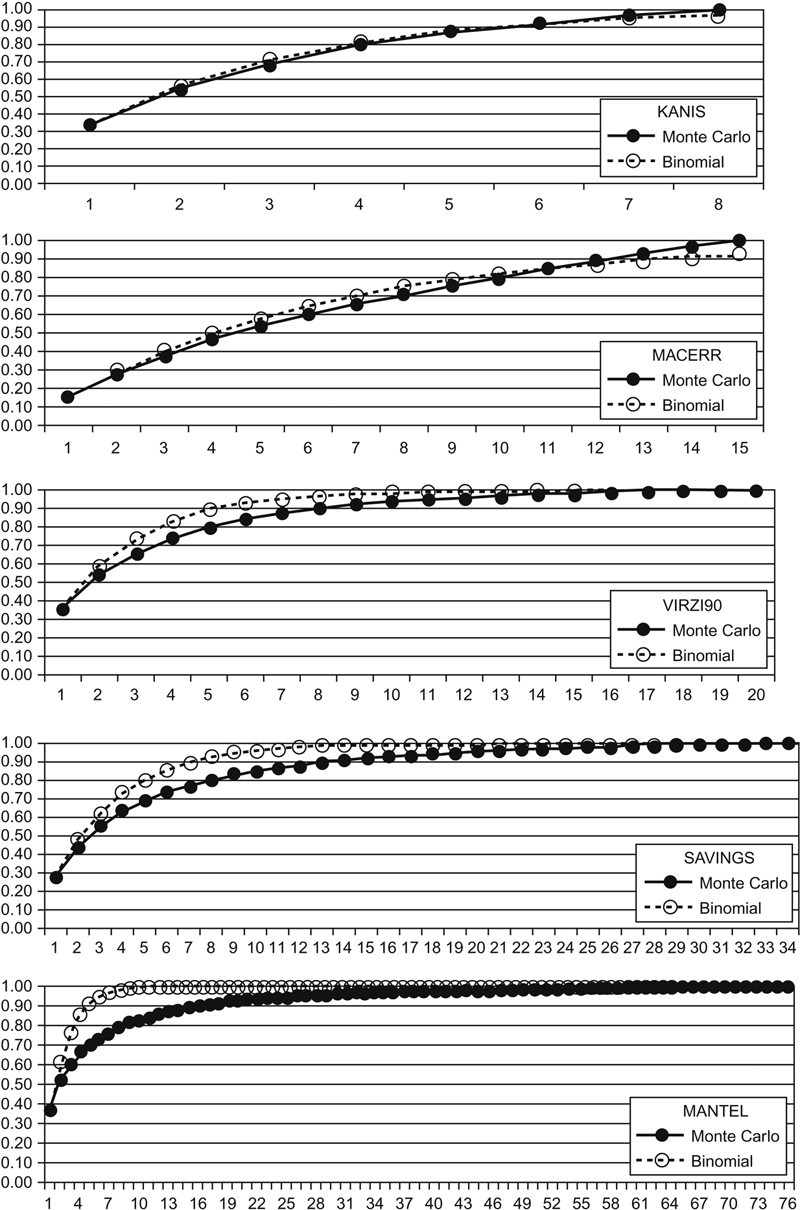
Table 7.9
Analyses of Maximum Differences Between Monte Carlo and Binomial Models for Five Usability Evaluations
| Database/Type of Evaluation | Total Sample Size | Total Number of Problems Discovered | Max Difference (Proportion) | Max Difference (Number of Problems) | At n = | p |
| KANIS (Usability Test) | 8 | 22 | 0.03 | 0.7 | 3 | 0.35 |
| MACERR (Usability Test) | 15 | 145 | 0.05 | 7.3 | 6 | 0.16 |
| VIRZI90 (Usability Test) | 20 | 40 | 0.09 | 3.6 | 5 | 0.36 |
| SAVINGS (Heuristic Evaluation) | 34 | 48 | 0.13 | 6.2 | 7 | 0.26 |
| MANTEL (Heuristic Evaluation) | 76 | 30 | 0.21 | 6.3 | 6 | 0.38 |
| Mean | 30.6 | 57.0 | 0.102 | 4.8 | 5.4 | 0.302 |
| Std Dev | 27.1 | 50.2 | 0.072 | 2.7 | 1.5 | 0.092 |
| N Studies | 5 | 5 | 5 | 5 | 5 | 5 |
| sem | 12.1 | 22.4 | 0.032 | 1.2 | 0.7 | 0.041 |
| df | 4 | 4 | 4 | 4 | 4 | 4 |
| t-crit-90 | 2.13 | 2.13 | 2.13 | 2.13 | 2.13 | 2.13 |
| d-crit-90 | 25.8 | 47.8 | 0.068 | 2.6 | 1.4 | 0.087 |
| 90% CI Upper Limit | 56.4 | 104.8 | 0.170 | 7.4 | 6.8 | 0.389 |
| 90% CI Lower Limit | 4.8 | 9.2 | 0.034 | 2.3 | 4.0 | 0.215 |

Pretend you are running a business. It is a high-risk business and you need to succeed. Now imagine two people come to your office:
• The first person says, “I’ve identified all problems we might possibly have.”
• The second person says, “I’ve identified the most likely problems and have fixed many of them. The system is measurably better than it was.”
Which one would you reward? Which one would you want on your next project? In our experience, businesses are far more interested in getting solutions than in uncovering issues.
Generally, we expect the MLE [maximum likelihood estimate] to perform better as the proportion of the population that is observed in a sample increases. The probability that a single individual detected with probability p is observed at least once in T capture occasions is 1 – (1 – p)T. Therefore, it is clear that increasing T is expected to increase the proportion of the population that is observed, even in situations where individual capture rates p are relatively small. In many practical problems T may be the only controllable feature of the survey, so it is important to consider the impact of T on the MLE’s performance.
Key points
Table 7.10
List of Sample Size Formulas for Formative Research
| Name of Formula | Formula | Notes |
The famous equation: 1 – (1 – p)n |
|
Computes the likelihood of seeing events of probability p at least once with a sample size of n—derived by subtracting the probability of 0 occurrences (binomial probability formula) from 1 |
| Sample size for formative research |
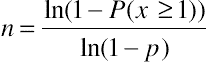
|
The equation above, solved for n—to use, set P(x > 1) to a discovery goal (for example, 0.85 for 85%) and p to the smallest probability of an event that you are interested in detecting in the study—ln stands for “natural logarithm” |
| Combined adjustment for small-sample estimates of p |

|
From Lewis (2001)—two-component adjustment combining deflation and Good-Turing discounting: pest is the estimate of p from the observed data; GTadj is the number of problem types observed only once divided by the total number of problem types |
| Quick adjustment formula |
|
Regression equation based on 19 usability studies—to use when problem-by-participant matrix not available |
| Binomial probability formula |

|
Probability of seeing exactly x events of probability p with n trials |












