CHAPTER IV
THE REAL GRASSMANNIANS
1. The real Grassmannians

The involutio![]() n of X, corresponding to the change of orientation of an m-plane of F, is an isometry of X. The group
n of X, corresponding to the change of orientation of an m-plane of F, is an isometry of X. The group ![]() of isometries of X generated by
of isometries of X generated by ![]() , which is of order 2, acts freely on X and we may consider the Riemannian manifold
, which is of order 2, acts freely on X and we may consider the Riemannian manifold ![]() endowed with the Riemannian metric gY induced by g. The natural projection
endowed with the Riemannian metric gY induced by g. The natural projection ![]() is a two-fold covering. We identify Y with the real Grassmannian
is a two-fold covering. We identify Y with the real Grassmannian ![]() of all m-planes in F. When m = 1, the Grassmannian
of all m-planes in F. When m = 1, the Grassmannian ![]() is the projective space of F.
is the projective space of F.
Let VY and WY be the vector bundles over Y whose fibers at the point y![]() Y are equal to Vx and Wx, respectively, where x is one of the points of X satisfying
Y are equal to Vx and Wx, respectively, where x is one of the points of X satisfying ![]() (x) = y. Then the tangent space T
(x) = y. Then the tangent space T![]() Y,y of Y at y Y is identified with
Y,y of Y at y Y is identified with ![]()
For x![]() X, the tangent space T(x) is equal to
X, the tangent space T(x) is equal to ![]() it is easily verified that the mappin
it is easily verified that the mappin![]() is equal to the identity mapping of
is equal to the identity mapping of ![]() A vector field on X is even (resp. odd) with respect to the involu
A vector field on X is even (resp. odd) with respect to the involu![]() tion if = (resp. = -). We say that a symmetric p-form u on X is even (resp. odd) with respect to
tion if = (resp. = -). We say that a symmetric p-form u on X is even (resp. odd) with respect to ![]() if
if ![]() where = 1 (resp.
where = 1 (resp.![]() = -1). Such a form u is even if and only if we can write
= -1). Such a form u is even if and only if we can write ![]() where
where ![]() is a symmetric p-form on Y . If E is a sub-bundle of
is a symmetric p-form on Y . If E is a sub-bundle of ![]() invariant under the isometry
invariant under the isometry![]() , there exists a unique sub-bundle EY of
, there exists a unique sub-bundle EY of ![]() such that, for all x
such that, for all x![]() X, the isomorphism
X, the isomorphism ![]() where y =
where y =![]() induces by restriction an isomorphism : E
induces by restriction an isomorphism : E![]() symmetric p-form u on Y is a section of EY if and only if the even symmetric p-form
symmetric p-form u on Y is a section of EY if and only if the even symmetric p-form ![]() on X is a section of E.
on X is a section of E.
Throughout the remainder of this section, we suppose that n 1. The curvature R of the Riemannian manifold (X, g) is determined by
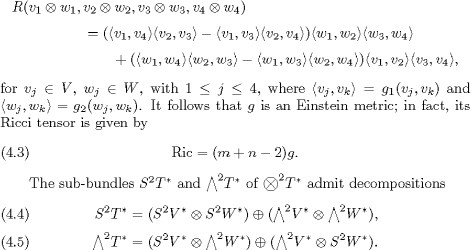
We denote by ![]() the sub-bundle of
the sub-bundle of ![]() which is the orthogonal complement, with respect to the scalar product induced by g1, of the line bundle {g1} generated by
the section g1 of
which is the orthogonal complement, with respect to the scalar product induced by g1, of the line bundle {g1} generated by
the section g1 of ![]() . Similarly, we denote by
. Similarly, we denote by ![]() Wthe sub-bundle of
Wthe sub-bundle of ![]() which is the orthogonal complement of the line bundle {g2} generated by the section g2. We consider the sub-bundles
which is the orthogonal complement of the line bundle {g2} generated by the section g2. We consider the sub-bundles

We also consider the Grassmannians ![]() = and
= and ![]() the natural projection :
the natural projection : ![]() and the involution of
and the involution of ![]() Let
Let ![]() be the canonical vector bundle of rank n over
be the canonical vector bundle of rank n over ![]() whose fiber at
whose fiber at ![]() is the subspace of F determined by the oriented n-plane a, and let
is the subspace of F determined by the oriented n-plane a, and let ![]() be the vector bundle of rank m over
be the vector bundle of rank m over ![]() whose fiber over a
whose fiber over a![]() Xis the orthogonal complement
Xis the orthogonal complement ![]() of
of ![]() in F. As above, we identify the tangent bundle of
in F. As above, we identify the tangent bundle of ![]() Xwith the bundle
Xwith the bundle ![]() the scalar product on F induces Riemannian metrics on
the scalar product on F induces Riemannian metrics on ![]() and
and ![]() . There is a natural diffeomorphism
. There is a natural diffeomorphism
![]()
sending an m-plane of F into its orthogonal complement. When m = n, this mapping is an involution of ![]() in this case, we say that a symmetric p-form u on Y is even (resp. odd) if
in this case, we say that a symmetric p-form u on Y is even (resp. odd) if ![]() where
where![]() = 1 (resp
= 1 (resp![]() . = -1).
. = -1).
Now suppose that the vector space F is oriented and let![]() be a unit vector of
be a unit vector of![]() which is positive with respect to the orientation of F. The oriented m-plane x
which is positive with respect to the orientation of F. The oriented m-plane x![]() X gives us an orientation of Vx, which in turn induces an orientation of Wx: if {v1, . . . , vm} is a positively oriented
orthonormal basis of Vx, then the orientation of Wx is determined by an orthonormal basis {w1, . . . ,wn} of Wx satisfying
X gives us an orientation of Vx, which in turn induces an orientation of Wx: if {v1, . . . , vm} is a positively oriented
orthonormal basis of Vx, then the orientation of Wx is determined by an orthonormal basis {w1, . . . ,wn} of Wx satisfying

endowed with the Riemannian metrics g and gY induced by the standard Euclidean scalar product of ![]() Throughout the remainder of this section, we also suppose that m + n 3.
Throughout the remainder of this section, we also suppose that m + n 3.
The group SO(m + n) acting on ![]() sends every oriented m-plane into another oriented m-plane. This gives rise to an action of the group SO(m + n) on X. In
fact, the group SO(m + n) acts transitively on the Riemannian manifold (X, g) by isometries. The isotropy group of the point
x0 of X corresponding to the vector e
sends every oriented m-plane into another oriented m-plane. This gives rise to an action of the group SO(m + n) on X. In
fact, the group SO(m + n) acts transitively on the Riemannian manifold (X, g) by isometries. The isotropy group of the point
x0 of X corresponding to the vector e![]() is the subgroup
is the subgroup ![]() of SO(m + n) consisting of the matrices
of SO(m + n) consisting of the matrices

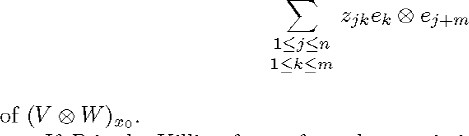
If B is the Killing form of ![]() the restriction to
the restriction to ![]() of the scalar product -B is invariant under the adjoint action of K and therefore induces an SO(m + n)-invariant metric
of the scalar product -B is invariant under the adjoint action of K and therefore induces an SO(m + n)-invariant metric ![]() on the homogeneous space SO(m + n)/K. Endowed with this metric g0, the manifold SO(m + n)/K is a symmetric space of compact
type of rank min(m, n). It is easily verified that
on the homogeneous space SO(m + n)/K. Endowed with this metric g0, the manifold SO(m + n)/K is a symmetric space of compact
type of rank min(m, n). It is easily verified that ![]() Thus is an isometry from the symmetric space SO(m + n)/K, endowed with the metric
Thus is an isometry from the symmetric space SO(m + n)/K, endowed with the metric
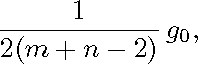
to X; henceforth, we shall identify these Riemannian manifolds by means of this SO(m + n)-equivariant isometry. From Lemma
1.21, we again obtain the equality (4.3). Moreover, the symmetric space SO(m + n)/K is irreducible unless m = n = 2. On the
other hand, we shall see below that the Grassmannian ![]() is not irreducible and is in fact isometric to a product of 2-spheres (see Proposition 4.3).
is not irreducible and is in fact isometric to a product of 2-spheres (see Proposition 4.3).



We now suppose that m = n = 3. If we identify the vector bundle ![]() with V and the vector bundle
with V and the vector bundle ![]() with W by means of the scalar products g1 on V and g2 on W, the Hodge operators
with W by means of the scalar products g1 on V and g2 on W, the Hodge operators

when m = n = 3. We recall that the Grassmannian ![]() is isometric to the symmetric space SU(4)/SO(4) (see [36, p. 519]). Thus by Lemma 2.41, we know that the space Hom
is isometric to the symmetric space SU(4)/SO(4) (see [36, p. 519]). Thus by Lemma 2.41, we know that the space Hom![]() vanishes for the space
vanishes for the space ![]() when m, n 3 and m + n 7, and that Hom
when m, n 3 and m + n 7, and that Hom![]() is one-dimensional for the space
is one-dimensional for the space ![]() as we have just seen, both of these assertions are also consequences of Lemma 4.1.
as we have just seen, both of these assertions are also consequences of Lemma 4.1.
Let ![]() be the element of the dual of the group SO(m + n) which is the equivalence class of the irreducible SO(m + n)-module
be the element of the dual of the group SO(m + n) which is the equivalence class of the irreducible SO(m + n)-module ![]() . We denote by K the SO(m + n)-module of all Killing vector fields on X and by KC its complexification. The irreducible symmetric
space X is not equal to
. We denote by K the SO(m + n)-module of all Killing vector fields on X and by KC its complexification. The irreducible symmetric
space X is not equal to![]() a simple Lie group. Thus according to (2.27), we know that the SO(m+n)module
a simple Lie group. Thus according to (2.27), we know that the SO(m+n)module ![]() is irreducible and is equal to KC. When m + n 7, by (4.16) the Frobenius reciprocity theorem tells us that
is irreducible and is equal to KC. When m + n 7, by (4.16) the Frobenius reciprocity theorem tells us that

(ii) If m = n = 3, then E(X) is an irreducible SO(6)-module isomorphic to the Lie algebra ![]() and is equal to the SO(6)-submodule
and is equal to the SO(6)-submodule
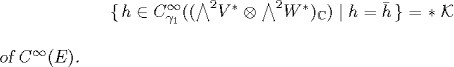
When m + n 7, the vanishing of the space E(X) is also given by Theorem 1.22 (see Koiso [41] and [42]).
For the remainder of this section, we suppose that m = n 2. Then the isometry![]() of the Grassmannian
of the Grassmannian ![]() is an involution. The group of isometries of Y generated by
is an involution. The group of isometries of Y generated by ![]() , which is of order 2, acts freely on Y and we may consider the Riemannian manifold
, which is of order 2, acts freely on Y and we may consider the Riemannian manifold ![]() equal to the quotient
equal to the quotient ![]() Y/endowed with the Riemannian metric
Y/endowed with the Riemannian metric ![]() induced by g. The natural projections
induced by g. The natural projections ![]() and
and ![]() are two-fold and four-fold coverings, respectively. The action of the group SO(2n) on Y passes to the quotient
are two-fold and four-fold coverings, respectively. The action of the group SO(2n) on Y passes to the quotient ![]() In fact, SO(2n) acts transitively on
In fact, SO(2n) acts transitively on ![]() and it is easily verified that the isotropy group of the point
and it is easily verified that the isotropy group of the point ![]() is equal to the subgroup of SO(2n) generated by
is equal to the subgroup of SO(2n) generated by ![]() and the matrix
and the matrix
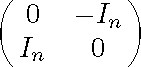
of SO(2n). In fact, ![]() is a symmetric space of compact type of rank n. When n 3, it is irreducible and equal to the adjoint space of X and of Y
. On the other hand, when n = 2, it is not irreducible, and we have the following result, whose proof appears below i
is a symmetric space of compact type of rank n. When n 3, it is irreducible and equal to the adjoint space of X and of Y
. On the other hand, when n = 2, it is not irreducible, and we have the following result, whose proof appears below i![]() n 9, Chapter V:
n 9, Chapter V:
PROPOSITION 4.3. The symmetric space (![]() endowed with the Riemannian metric which is the product of the metrics of constant curvature 1 on each factor is isometric
to the Grassmannian
endowed with the Riemannian metric which is the product of the metrics of constant curvature 1 on each factor is isometric
to the Grassmannian ![]() endowed with the Riemannian metric
endowed with the Riemannian metric ![]() Y ).
Y ).
The following proposition is a direct consequence of Propositions 4.3 and 10.2, and of Theorem 2.23,(ii).
PROPOSITION 4.4. The maximal flat Radon transform for functions on the symmetric space ![]() G
G
R2 ,2 is injective.
The notion of even or odd tensor on Y (with respect to the involutive isometry ![]() defined here coincides with the one considered in 4, Chapter II. In fact, a section u of
defined here coincides with the one considered in 4, Chapter II. In fact, a section u of ![]() over Y is even if and only if we can write
over Y is even if and only if we can write ![]() where
where ![]() is a symmetric p-form on
is a symmetric p-form on ![]() Y . Lemma 2.17 gives us the following result:
Y . Lemma 2.17 gives us the following result:
LEMMA 4.5. A symmetric p-form u on ![]() satisfies the Guillemin condition if and only if the even symmetric p-form
satisfies the Guillemin condition if and only if the even symmetric p-form ![]() on
on ![]() satisfies the Guillemin condition.
satisfies the Guillemin condition.
![]() 2. The Guillemin condition on the real Grassmannians
2. The Guillemin condition on the real Grassmannians
Let m, n 1 be given integers. In this section, we again consider the real Grassmannians X = ![]() and Y =
and Y = ![]() endowed with the metrics g and gY , and the natural Riemannian submersion
endowed with the metrics g and gY , and the natural Riemannian submersion ![]() and continue to identify the tangent bundle T of X with the vector bundle
and continue to identify the tangent bundle T of X with the vector bundle ![]() as in
as in![]() 1.
1.

of closed totally geodesic submanifolds of ![]() Indeed, using the above description of the mappin
Indeed, using the above description of the mappin![]() at (x1, . . . , xr), we see that the tangent spaces of these two submanifolds of
at (x1, . . . , xr), we see that the tangent spaces of these two submanifolds of ![]() at x are equal. From the formula for the curvature of
at x are equal. From the formula for the curvature of ![]() we infer that ExpxV 1 W1 is a totally geodesic submanifold of
we infer that ExpxV 1 W1 is a totally geodesic submanifold of ![]() and a globally symmetric space. Clearly, the sub-manifold
and a globally symmetric space. Clearly, the sub-manifold ![]() possesses these same properties. In fact, the subgroup SO(m+n, V1) of SO(m+n) consisting of all elements of SO(m+n) which
preserve the subspace V1 and which are the identity on the orthogonal complement of V1 acts transitively on these submanifolds
by isometries. These various observations yield the relation (4.21), which in turn gives us the equality
possesses these same properties. In fact, the subgroup SO(m+n, V1) of SO(m+n) consisting of all elements of SO(m+n) which
preserve the subspace V1 and which are the identity on the orthogonal complement of V1 acts transitively on these submanifolds
by isometries. These various observations yield the relation (4.21), which in turn gives us the equality

From the above observations and the equalities (4.21) and (4.22), we obtain:

(ii) if u is an even (resp. odd) symmetric form on X, the form ![]() iu on Z is even (resp. odd);
iu on Z is even (resp. odd);
(iii) if h is a section of the sub-bundle E of ![]() over X, then
over X, then ![]() ih is a section of the sub-bundle EZ of
ih is a section of the sub-bundle EZ of ![]() .
.
If the subspaces Vj are all 2-dimensional and the integers pj are all equal to 1, then the images of the mappings![]() and are totally geodesic flat r-tori of
and are totally geodesic flat r-tori of ![]() and
and ![]() In particular, when m
In particular, when m ![]() n and r = m, these images are maximal flat totally geodesic tori of
n and r = m, these images are maximal flat totally geodesic tori of ![]() and
and ![]() and all maximal flat totally geodesic tori of
and all maximal flat totally geodesic tori of ![]() and
and ![]() arise in this way. On the other hand when n < m and r = n + 1, if the subspaces Vj are 2-dimensional and pj = 1 for
arise in this way. On the other hand when n < m and r = n + 1, if the subspaces Vj are 2-dimensional and pj = 1 for ![]() and if
and if ![]() = m - n, then the images
= m - n, then the images
m-From Lemma 2.17, or from the commutativity of diagram (4.23) and the above remarks concerning totally geodesic flat tori of the Grassmanni-ans, we obtain the following result:
LEMMA 4.7. A symmetric p-form u on Y satisfies the Guillemin condition if and only if the even symmetric p-form ![]() on X satisfies the Guillemin condition.
on X satisfies the Guillemin condition.

of Y , which is isometric to ![]() If u is a symmetric p-form on Y satisfying the Guillemin condition, then the restriction of u to
If u is a symmetric p-form on Y satisfying the Guillemin condition, then the restriction of u to ![]() satisfies the Guillemin condition.
satisfies the Guillemin condition.

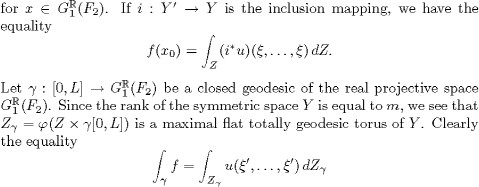
holds. Now we suppose that u satisfies the Guillemin condition; then the above integral vanishes, and so the function f on
the real projective space ![]() of dimension
of dimension![]() 2 satisfies the zero-energy condition. The injec-tivity of the X-ray transform for functions on the real projective space
of dimension
2 satisfies the zero-energy condition. The injec-tivity of the X-ray transform for functions on the real projective space
of dimension ![]() 2, given by Theorem 2.23,(ii), tells us that the function f vanishes. From the equality f(x0) = 0, we infer that the restriction
of u to
2, given by Theorem 2.23,(ii), tells us that the function f vanishes. From the equality f(x0) = 0, we infer that the restriction
of u to ![]() satisfies the Guillemin condition.
satisfies the Guillemin condition.
The following proposition is a generalization of Lemma 5.3 of [23].


From Proposition 4.10 and Lemma 4.6, by means of the isometries : GR ,p we deduce the following: ![]()
PROPOSITION 4.12. Let y be a point of the real Grassmannian Y = ![]() Let
Let ![]() be a closed totally geodesic submanifold of Y isometric to the real Grassmannian
be a closed totally geodesic submanifold of Y isometric to the real Grassmannian ![]() which can be written in the form Expy
which can be written in the form Expy![]() where
where ![]() is a q-dimensional subspace of V
is a q-dimensional subspace of V![]() and
and ![]() is an r-dimensional subspace of
is an r-dimensional subspace of ![]() Assume either that 2
Assume either that 2 ![]() m < n and r = n, or that 2 n < m and q = m. If u is a symmetric p-form on Y satisfying the Guillemin condition, then the restriction
of u to
m < n and r = n, or that 2 n < m and q = m. If u is a symmetric p-form on Y satisfying the Guillemin condition, then the restriction
of u to ![]() satisfies the Guillemin condition.
satisfies the Guillemin condition.
When ![]() the following proposition is a consequence of Propositions 4.11 and 4.12 and Lemma 4.6. If
the following proposition is a consequence of Propositions 4.11 and 4.12 and Lemma 4.6. If ![]() in the following proposition, the submanifold
in the following proposition, the submanifold ![]() of Y considered there has the same rank as Y , and in this case the conclusion of the proposition is immediate.
of Y considered there has the same rank as Y , and in this case the conclusion of the proposition is immediate.
PROPOSITION 4.13. Let y be a point of the real Grassmannian Y = ![]() with 2
with 2 ![]() m < n. Let
m < n. Let ![]() Y be a closed totally geodesic submanifold of Y isometric to the real Grassmannian
Y be a closed totally geodesic submanifold of Y isometric to the real Grassmannian ![]() which can be written in the form
which can be written in the form ![]() where
where ![]() is a q-dimensional subspace of
is a q-dimensional subspace of ![]() If u is a symmetric p-form on Y satisfying the Guillemin condition, then the restriction of u to
If u is a symmetric p-form on Y satisfying the Guillemin condition, then the restriction of u to ![]() satisfies the Guillemin condition.
satisfies the Guillemin condition.
From Proposition 4.12 and the injectivity of the X-ray transform for functions on a real projective space, we now obtain the following proposition, which is also given by Theorem 2.24.
PROPOSITION 4.14. For m, ![]() n 2, with
n 2, with ![]() the maximal flat Radon transform for functions on the real Grassmannian
the maximal flat Radon transform for functions on the real Grassmannian ![]() is injective.
is injective.

PROOF: Let Z be the closed totally geodesic submanifold of Y equal ,n; clearly to Expy![]() which is isometric to the real Grassmannian
which is isometric to the real Grassmannian ![]() is a totally geodesic submanifold of Z. Let
is a totally geodesic submanifold of Z. Let![]() be a 1-form on Y satisfying the Guillemin condition. By Proposition 4.12, the restriction of
be a 1-form on Y satisfying the Guillemin condition. By Proposition 4.12, the restriction of![]() to the submanifold Z satisfies the zero-energy condition; therefore so does the restriction
to the submanifold Z satisfies the zero-energy condition; therefore so does the restriction ![]() of to the submanifold
of to the submanifold ![]() By Theorem 3.26, we know that is exact.
By Theorem 3.26, we know that is exact.
