From the above discussion concerning the parallel vector fields on the totally geodesic flat 2-torus Z and from the relations (6.8), we deduce the following result:

PROPOSITION 6.3. Let h be a section of over , with n 3. The symmetric 2-form h satisfies the Guillemin condition if and only if the two symmetric 2-forms and satisfy the Guillemin condition.

Let N be an odd integer 1; we consider the closed geodesic

3. Symmetric forms on the complex quadric

We now introduce certain symmetric 2-forms on X which are defined in [23, 4]; we shall also recall some of their properties which are established in [23].

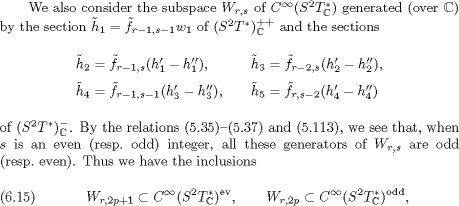
for all p 0. Lemma 7.7 of [23] asserts the following:

LEMMA 6.5. Let r, s 0 be given integers. The non-zero elements of the set of generators of the space form a basis of . More precisely, the dimensions and bases of the non-zero spaces are given by the following table:

LEMMA 6.6. If the non-zero elements of the set of generators of the spaces and form bases of these spaces. More precisely, the dimensions and bases of the non-zero spaces and are given by the following table:

4. Computing integrals of symmetric forms

In this section and the next one, we shall compute integrals of symmetric 2-forms over specific closed geodesics of X. Each of these geodesics is contained in one of the families of flat 2-tori of X considered in [23, 4]. Thus many of the computations appearing in these two sections of this chapter are the same or similar to those of [23, 4].

We consider the torus Z₀ introduced in 2 and we shall use the objects associated there with this torus. In particular, we shall identify a function f on satisfying

for Since cos2 t sin2(r+s) t 0, the lemma is a consequence of the equality (6.13) and the above relation.

Let be a given real number; we set ì = cos and = sin . If is the inclusion mapping of the complex hypersurface V into V , the symmetric 2-forms and on satisfy the relations

LEMMA 6.10. Let r, s 0 be given integers. Then there exists 0

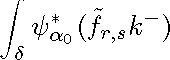
does not vanish.

PROOF: The coefficient of of the polynomial is equal

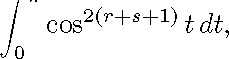
which is positive, and so the polynomial is non-zero. Hence there exists a real number such that the expressions cos 0 and do not vanish. Therefore by (6.12) and (6.22), we infer that the integral of the lemma corresponding to this element does not vanish.

Let be the element of G defined by

5. Computing integrals of odd symmetric forms

This section is a continuation of the preceding one. Its results will only be used in the proofs of the lemmas of 6, which we require for Propositions 6.28 and 6.34 and for Theorem 6.36. This last theorem is needed in 8 to establish the infinitesimal rigidity of the quadric of dimension 3.

If k, l 0 are given integers, we set

does not vanish.

LEMMA 6.14. Let r 0 and s 2 be given integers, with s even. Then there exists such that the integral

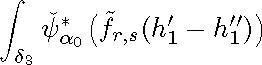
does not vanish.

Let r 0 and s 1 be given integers. Since the elements of G induce isometries of X, according to Lemmas 6.13 and 6.14, the symmetric

PROOF: By formulas (6.32) and (6.35), there exists an explicit polynomial P(u) of degree 3 in u such that

holds.

PROOF: By formulas (6.32) and (6.37), there exists an explicit polynomial of degree 3 in u such that

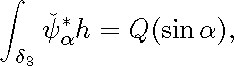
for moreover, we verify that the coefficient of u2 of is equal to

If the symmetric 2-form h satisfies the zero-energy condition, the polynomial Q vanishes and so, by Lemma 6.12, we obtain the relation (6.38).

PROOF: By (6.30) and the formulas involving which appear after Lemma 6.15, we obtain expressions for the functions on Z0, with 1 j 8. By the relations (6.11)–(6.13), with N = 1, there exists an explicit polynomial P(u) of degree in u such that

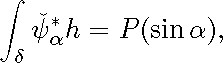
for all R. Since the symmetric 2-form h satisfies the zero-energy condition, this polynomial P vanishes. The vanishing of the coefficient of of P(u) gives us the relation (6.41). Next, we give equalities analogous to those appearing after Lemma 6.14, with replaced by the element of G defined in 4. Then by (6.19) and these formulas, we obtain expressions for the functions on Z0, with 1 j 8. Using relations (6.11)–(6.13), with N = 1, we compute an explicit polynomial of degree in u such that

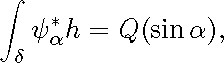
for Our hypotheses imply that this polynomial vanishes. The vanishing of the coefficient of (resp. of gives us the relation (6.39) (resp. the relation (6.40)). Moreover, when r is odd, the equality (- = 0 is equivalent to (6.42), while the equality = 0 is equivalent to (6.43). On the other hand, when r is even, the equality Q(1) = 0 is equivalent to (6.44), while the equality = 0 is equivalent to (6.45).

Let r, s 0 be fixed integers; we now consider the sections with defined in 3.

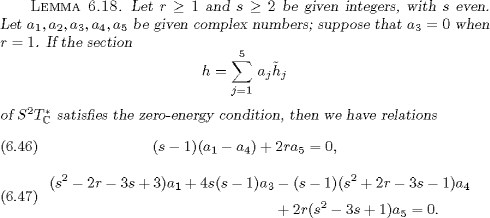
PROOF: We first derive equalities analogous to (6.30) and to those appearing after Lemma 6.14, with replaced by , with Since we have = ,0, these new formulas generalize those given above; we also remark that . We then obtain expressions for the ,functions and

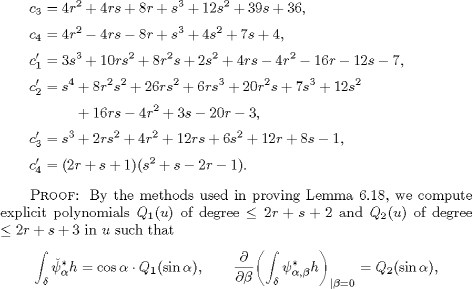
for all If the symmetric 2-form h satisfies the zero-energy condition, the polynomials Q1 and Q2 vanish; the vanishing of the coefficients of and in the polynomial Q1(u) give us the relations (6.48) and (6.49), respectively, while the vanishing of the coefficient of in the polynomial Q2(u) give us the relation (6.50).

LEMMA 6.20. Let r, s 0 be given integers, with s even, and let a1, a2, a3, a4 be given complex numbers. Suppose that a3 = 0 when r = 0, and that a4 = 0 when s = 0. If the section

for Here we require formulas (6.19) and (6.21) and certain formulas used in proving Lemma 6.17. The equality P(0) = 0 is equivalent to (6.52), while the equality = 0 is equivalent to (6.51). On the other hand, when r is even, the equality P(1) = 0 is equivalent to (6.53). When r is odd, the equality P(-1) = 0 is equivalent to the relation

We easily see that the relations (6.52) and (6.54) imply that (6.53) holds. If the symmetric 2-form h satisfies the zero-energy condition, the polynomial P vanishes, and we obtain the desired equalities.

LEMMAS 6.17–6.20 are due to Tela Nlenvo; details of the proofs of these lemmas can be found in [52].

6. Bounds for the dimensions of spaces of symmetric forms

In this section, we use the results of 4 and 5 to give bounds for the dimension of certain spaces which we shall need in 7.

LEMMA 6.21. Let r, s 0 be given integers, with s even. Then we have

PROOF: For r 1, s 2, the determinant of the matrix, whose entries are the coefficients of a1, a2 and a3 in the relations (6.51), (6.52) and (6.53), is equal to

If r = 0 and s 2 (resp. if r 1 and s = 0), the relations (6.51) and (6.52), with a3 = 0 (resp. with a4 = 0), are clearly linearly independent. Finally, if r = s = 0, the relations (6.51), (6.52) and (6.53) reduce to a1 + a2 = 0. We remark that the symmetric 2-form h of Lemma 6.20 is an element of From Lemmas 6.6 and 6.20, we then deduce the desired inequality.

LEMMA 6.22. Let r, s 0 be given integers, with s even. Then we have

PROOF: If r 1, the determinant of the matrix, whose entries are the coefficients of a2, a3 and a4 in the relations (6.48), (6.49) and (6.50), is equal to

If r = 0, the relations (6.48) and (6.50), with a3 = 0, are linearly independent; in fact, the determinant of the matrix, whose entries are the coefficients of a2 and a4 in these two relations, is equal to -8(s + 1)2. We remark that the symmetric 2-form h of Lemma 6.19 is an element of From Lemmas 6.6 and 6.19, we then obtain the desired inequality.

LEMMA 6.23. Let r, s 0 be given integers, with s even. Then we have

PROOF: If r, s 2, the determinant of the matrix, whose entries are the coefficients of a3 and a4 in the relations (6.46) and (6.47), is equal to the non-zero expression 4s(s - 1)2. If r = 1 and s 2, or if r 2 and s = 0, the relation (6.46) is non-trivial. We note that the relations (6.46) and (6.47) do not involve the coefficient a2; when r 1 and s 2, according to Lemma 6.14, the symmetric 2-form which belongs to does not satisfy the zero-energy condition. We remark that the symmetric 2-form h of Lemma 6.18 is an element of These observations, together with Lemmas 6.5 and 6.18, give us the desired inequality.

LEMMA 6.24. Let r 0, s 1 be given integers, with s odd. Then we have

PROOF: We note that the relations (6.39)–(6.45) do not involve the coefficient when r 1 and 2r + s - 3 > 0, according to Lemma 6.13, the symmetric 2-form h4, which belongs to does not satisfy the zero-energy condition. Also the symmetric 2-form h of Lemma 6.17 is an element of r,s.

(i) We first consider the case when r, s 3 and r is odd. In view of the above observations and Lemmas 6.4 and 6.17, it suffices to show that the matrix, corresponding to the linear system consisting of the equations (6.39)–(6.43) in the scalars aj , with 1 j 8 and j = 4, is of maximal rank. The determinant of the matrix, whose entries are the coefficients of the aj , with j = 1 and 5 in these relations, is equal to

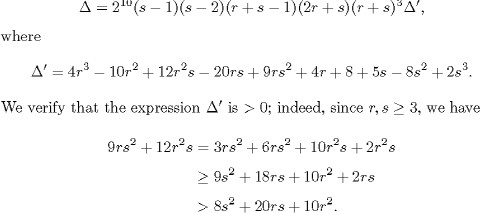
Therefore the determinant is > 0 and our 5 × 7 matrix is of maximal rank.

(ii) We next consider the case when r 2 is even and s 3. In view of the observations which precede the case (i), and Lemmas 6.4 and 6.17, it suffices to show that the matrix, corresponding to the linear system consisting of the equations (6.39)–(6.41), and (6.44) and (6.45) in the scalars aj , with 1 8 and is of maximal rank. The determinant of the 5 × 5 matrix, whose entries are the coefficients of the aj , with j = 1 and in these relations, is equal to

Since 2r +s-3 = s-1 > 0, in view of the observations which precede the case (i), and Lemmas 6.4 and 6.17, it suffices to show that the matrix, corresponding to the linear system consisting of equations (6.55)–(6.58) in the scalars aj , with 1 8 and j 4, 5, is of maximal rank. The determinant of the 4 × 4 matrix, whose entries are the coefficients of the scalars a1, a2, a3, a6 in the equations (6.55)–(6.58), is equal to

Since 2r+s-3 = 2r-2 > 0, in view of the observations which precede the case (i), and Lemmas 6.4 and 6.17, when r is odd (resp. even) it suffices to know that the matrix corresponding to the linear system consisting of equations (6.59)–(6.61) (resp. of equations (6.59), (6.60) and (6.62)) in the scalars a1, a2, a5, a6, a8 is of maximal rank. Since the determinant of the matrix

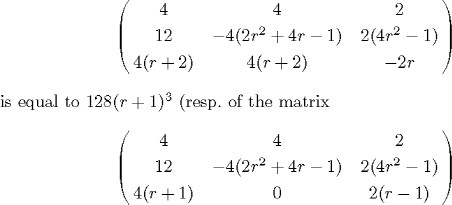
is equal to 128r( r + 1)2), our matrix is of maximal rank when r is odd (resp. even).

in this case, we also consider the relation (6.38) of Lemma 6.16. Since the determinant of the matrix

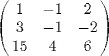
is equal to 104, the matrix of the linear system consisting of equations (6.65), (6.67) and (6.38) in the scalars a1, a3, a7, a8 is of maximal rank. For all s 3, we then obtain the desired inequality from Lemmas 6.4, 6.16 and 6.17.

(vii) We finally consider the case when r = 0 and s = 1. In this case, we set

and then Lemmas 6.4 and 6.17 imply the desired result.

7. The complex quadric of dimension three

In this section, we suppose that n = 3 and that X is the quadric of dimension 3, which is a homogeneous space of the group G = SO(5). Let be the dual of the group G.

The Casimir element of the Lie algebra g0 of G operates by a scalarcon an irreducible G-module which is a representative of . We know that, for , the G-module is an eigenspace of the Lich-nerowicz Laplacian with eigenvalue = 12c. If W is a G-submodule of with , we denote by C(W) the weight subspace of W corresponding to its highest weight ; we recall that the multiplicity of the G-module W is equal to the dimension of the space C(W).

From the branching law for SO(5) and its subgroup K described in Theorem 1.2 of [54], using the computation of the highest weights of the irreducible K-modules given in 7, Chapter V, we obtain the following result given by Proposition 9.1 of [23] (see also [54, 4]):

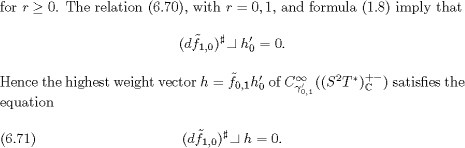
Moreover since the section h is either even or odd, we know that one (and only one) of the coefficients c1, c2 must vanish. If c2 = 0, then from (6.71) we obtain the relation

which contradicts (6.69). Therefore we must have c1 = 0, and the vector h is a non-zero multiple of k- and so is an odd section of Hence the vector satisfies the conclusion of the lemma.

For r 0, the highest weight vector of the SO(5)-module C((S2T)C+-)^ev generates (over C) a subspace V r,0 of this module. By Lemma 6.30 we have

for r, s 0, and so the symmetric 2-form belongs to the subspace for all r, s 0.

From Proposition 6.25, Lemma 6.6, the inclusions (6.16) and the remark preceding Lemma 6.30, we deduce the following result given by Lemma 9.5 of [23]:

LEMMA 6.31. For r, s 0, we have

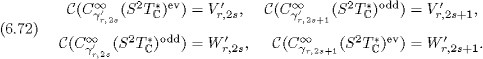
LEMMA 6.32. For r, s 0, with s even, the symmetric 2-form on X does not satisfy the Guillemin condition.

For r 0, we have From Proposition 5.22 and from Lemmas 6.8, 6.29, 6.31 and 6.32, we then obtain the following result:

PROPOSITION 6.33. For r, s 0, we have

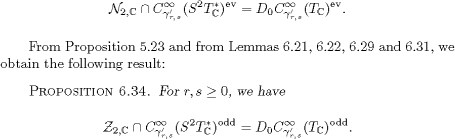
We now complete the proof of the following result of [23].

THEOREM 6.35. An even symmetric 2-form on the quadric X = satisfies the Guillemin condition if and only if it is a Lie derivative of the metric.

PROOF: From Proposition 2.30,(i), with , and and Propositions 6.25, 6.27 and 6.33, we obtain the equality

which implies the desired result.

The following is a consequence of joint work with Tela Nlenvo (see [52] and 5).

THEOREM 6.36. An odd symmetric 2-form on the quadric satisfies the zero-energy condition if and only if it is a Lie derivative of the metric.

PROOF: From Proposition 2.30,(ii), with and and Propositions 6.25, 6.28 and 6.34, we obtain the equality

which implies the desired result.

Let r, s 0 be given integers. By Lemma 4.5 of [23], when s 2 is even, the highest weight vector

PROPOSITION 6.37. Let X be the complex quadric Q3. For r, s 0, we have

The following theorem is a direct consequence of Propositions 5.24, 6.25 and 6.37.

THEOREM 6.38. An even section of over the quadric which satisfies the Guillemin condition, vanishes identically.

Let r 0, s 1 be given integers. By Lemma 6.9, when s is an odd integer, the highest weight vector

PROPOSITION 6.39. Let X be the complex quadric Q3. For r, s 0, we have

The following theorem is a direct consequence of Propositions 5.25, 6.25 and 6.39.

THEOREM 6.40. An odd section of over the quadric Q3, which satisfies the zero-energy condition, vanishes identically.

8. The rigidity of the complex quadric

In this section, we assume that X is the complex quadric with n 3, and we extend the main results of 7 to the quadric Qn; in particular, we shall prove the four following theorems.

THEOREM 6.41. An even symmetric 2-form on the quadric X = Qn, with n 3, satisfies the Guillemin condition if and only if it is a Lie derivative of the metric.

THEOREM 6.42. An odd symmetric 2-form on the quadric X = Qn, with n 3, satisfies the zero-energy condition if and only if it is a Lie derivative of the metric.

THEOREM 6.43. An even section of over the quadric Qn, with n 3, which satisfies the Guillemin condition, vanishes identically.

THEOREM 6.44. An odd section of ( over the quadric Qn, with n 3, which satisfies the zero-energy condition, vanishes identically.

From Theorems 6.41 and 6.42, we shall deduce the following:

THEOREM 6.45. The complex quadric X = Qn, with n 3, is infinitesimally rigid.

From Theorems 6.43 and 6.44, we shall deduce the following:

THEOREM 6.46. A section of over the complex quadric Qn, with n 3, which satisfies the zero-energy condition, vanishes identically.

We now prove these last two theorems simultaneously. Let h be a symmetric 2-form on X satisfying the zero-energy condition. We write where

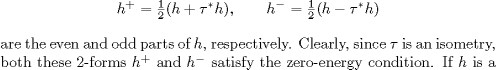
section of so are the forms h+ and h-. By Lemma 2.11, the even form h+ satisfies the Guillemin condition. First, by Theorems 6.41 and 6.42 we know that the even form h+ and the odd form h- are Lie derivatives of the metric. Finally, if h is a section of by Theorems 6.43 and 6.44 we know that the forms h+ and h- vanish.

From Theorems 6.41 and 6.43, and from Propositions 2.18 and 2.21, with and F = E = we deduce the following two results:

THEOREM 6.47. The real Grassmannian Y = with n 3, is rigid in the sense of Guillemin.

THEOREM 6.48. A section of the vector bundle EY over the real Grassmannian with n 3, which satisfies the Guillemin condition, vanishes identically.

of submanifolds of X and we saw that a submanifold of X belonging to Fis isometric to the complex quadric of dimension 3.

From Lemma 4.8, with p = 2 and q = 3, we obtain:

LEMMA 6.49. Let X be the complex quadric with n 3. Let

xx and h be an element of If the restriction of h to an arbitrary submanifold of the family Fvanishes, then h vanishes.

PROPOSITION 6.50. Let h be a symmetric 2-form on the quadric X = Qn, with n 3.

PROOF: We consider the complex quadric Z = of dimension 3. Let be a submanifold of X belonging to the family According to Lemma 4.6 and the equality (5.64), there is a totally geodesic imbedding whose image is equal to and which possesses the following properties:

We note that Proposition 6.50,(iii) gives us Theorems 6.43 and 6.44. We therefore know that Theorem 6.46 also holds.

We consider the G-invariant family F = F1 of closed connected totally geodesic surfaces of X defined in 6, Chapter V; there we saw that each surface of F is contained in a totally geodesic submanifold belonging to the family and that all the totally geodesic flat 2-tori of X belong to the family F. Thus any closed geodesic of X is contained in a totally geodesic surface of X belonging to the family F; it follows that

According to the inclusion (6.73) and Theorem 6.46, we know that the equality

holds. By Lemma 5.8, relation (6.74) and Proposition 5.17, we see that the families F and and the vector bundle satisfy the hypotheses of Theorem 2.48,(iii). Hence from this theorem, we deduce the following result:

This theorem together with the first two parts of Proposition 6.50 implies Theorems 6.41 and 6.42. According to the proofs of Theorem 2.45,(iii) and Proposition 6.50, we see that the only results of 7 which we require for the proof of Theorem 6.41 (resp. Theorem 6.42) are Theorems 6.35 and 6.38 (resp. Theorem 6.36 and 6.40).

None of our results concerning forms on the quadric satisfying the zero-energy condition enter into our proof of Theorem 6.41 given above. Previously, in [23] we deduced Theorem 6.41 for the quadric with n 4, from Theorem 6.35 by means of the infinitesimal rigidity of this quadric. In fact, if h is an even symmetric 2-form on X = Qn, with n 4, satisfying the Guillemin condition, by Proposition 6.50,(i) and the inclusion (6.73) we know that h satisfies the zero-energy condition; the infinitesimal rigidity of Qn implies that h is a Lie derivative of the metric.

From Theorems 5.27 and 6.41, we obtain the following:

THEOREM 6.52. An even section of L over the quadric with n 3, which satisfies the Guillemin condition, vanishes identically.

From Theorem 6.41 and the decomposition (1.11), we obtain the relation

9. Other proofs of the infinitesimal rigidity of the quadric

In this section, we suppose that X is the complex quadric , with n 4. This section and the next one are devoted to other proofs of the infinitesimal rigidity of the quadric X = with n 4. Some of the methods used here were introduced in [18] and [22].

The essential aspects of the proof of the following proposition were first given by Dieng in [10].

PROPOSITION 6.53. The infinitesimal rigidity of the quadric implies that all the quadrics Qn, with n 3, are infinitesimally rigid.

PROOF: We consider the G-invariant family F3 of closed connected totally geodesic surfaces of X introduced in 6, Chapter V and the family of closed connected totally geodesic submanifolds of X isometric to the quadric Q3 introduced in 6, Chapter V and in 8. According to a remark made in 6, Chapter V, we know that each surface belonging to the family F3 is contained in a totally geodesic submanifold of X belonging to the family Assume that we know that the quadric Q3 is infinitesimally rigid; then the family possesses property (III) of 8, Chapter II; moreover, by Propositions 5.13 and 5.14, the families F = F3 and satisfy the hypotheses of Theorem 2.47,(iii). From this last theorem, we deduce the infinitesimal rigidity of X.

We now consider the G-invariant family F = F2 of closed connected totally geodesic surfaces of X. The sub-bundle N2 = NF of B consisting of those elements of B, which vanish when restricted to the closed totally geodesic submanifolds of F, was introduced in 8, Chapter II and was considered in 6, Chapter V. We also consider the differential operator

of 8, Chapter II.

We consider the families and of closed connected totally geodesic submanifolds of X introduced in 6, Chapter V and we set

A submanifold of X belonging to (resp. to is a surface isometric to the flat 2-torus (resp. to the real projective plane , while a submanifold of X belonging to is isometric to the complex projective space CP2. In 6, Chapter V, we saw that each surface belonging to is contained in a submanifold of X belonging to the family therefore each surface of X belonging to F is contained in a submanifold of X belonging to the family According to Proposition 3.19 and Theorems 3.7 and 3.39, we see that the family possesses property (III) of 8, Chapter II. Hence a symmetric 2-form h on X satisfying the zero-energy condition belongs to ) and, by Proposition 2.44, verifies the relation

vanishes identically.

We now give an alternate proof of Theorem 6.45, with n 4, using Propositions 6.54, 6.55 and 5.26. In the case n = 4, this proof appears in [22]. Let h be a symmetric 2-form on the quadric X = Qn, with n 4, satisfying the zero-energy condition and the relation div h = 0. When n 5, Proposition 6.54 tells us that h is a section of L; by Proposition 5.26, we see that h vanishes identically. When n = 4, Proposition 6.54 tells us that h is a section of and, as we saw above, Proposition 2.44 gives us the relation by Proposition 6.55, we see that h vanishes. Then Proposition 2.13 gives us the infinitesimal rigidity of X.

Finally, we present an outline of the proof of the infinitesimal rigidity of Qn, with n 5, given in [18]. This proof completely avoids the use of harmonic analysis on the quadric; it requires the description of the explicit complement of in the vector bundle N2 = NF given by Proposition 5.12.

By Lemma 1.17, we obtain the relation (6.76). Then Proposition 6.56 tells us that v = 0 and Since a harmonic differential 2-form on X is a constant multiple of the Kahler form of X, we immediately deduce that Thus we know that D1h = 0. We know that the sequence (1.24) is exact (see 6, Chapter V); therefore h is a Lie derivative of the metric. We have thus shown that the infinitesimal rigidity of the quadric with is a consequence of Propositions 5.12, 5.14 and 6.56.

10. The complex quadric of dimension four

In this section, we suppose that X is the complex quadric Q4 of dimension 4, which is a homogeneous space of the group G = SO(6), and we present an outline of the proof of Proposition 6.55.

11. Forms of degree one

PROPOSITION 6.68. The space g(K) belongs to the kernel of and is isomorphic to the cohomology of the complex (6.87), with j = 1.

PROOF: By Proposition 3.10,(i), we know that g(K) belongs to the kernel of Let be a 1-form on X satisfying = 0. We consider

PROPOSITION 6.69. An even 1-form on X satisfying the Guillemin condition verifies the relation

From Propositions 2.20, 6.67 and 6.69, we deduce the following two results given by Theorems 11.1 and 11.2 of [23]:

THEOREM 6.70. An even 1-form on the quadric with n 3, satisfies the Guillemin condition if and only if it is exact.

THEOREM 6.71. A 1-form on the Grassmannian with n 3, satisfies the Guillemin condition if and only if it is exact.

The following result is given by Theorem 2 of [20].

THEOREM 6.72. A 1-form on the quadric X = with n 3, satisfies the zero-energy condition if and only if it is exact.

PROOF: Let be a 1-form on X satisfying the zero-energy condition. From Theorem 3.8, it follows that the restriction of to a flat torus of X belonging to the family is exact. Therefore we have According to Proposition 6.68, we may write

When n 4, we are able to give a proof of the preceding theorem which avoids the use of Proposition 6.68. In 6, Chapter V, we saw that each surface belonging to the family F2 is contained in a submanifold belonging to the family of closed totally geodesic submanifolds of X introduced there. Since a submanifold belonging to the family is isometric to the complex projective space according to Theorems 3.8 and 3.40 we know that the family possesses property (VI) of 8, Chapter II. When n 4, Theorem 6.72 is thus a consequence of the last equality of (6.86) and Theorem 2.51,(ii), with F = and .