CHAPTER VII

THE RIGIDITY OF THE REAL GRASSMANNIANS

1. The rigidity of the real Grassmannians

We consider the G-invariant families

of closed connected totally geodesic submanifolds of X. We consider the sub-bundle N = NF of B introduced in 8, Chapter II consisting of those elements of B, which vanish when restricted to the closed totally geodesic submanifolds of F.

LEMMA 7.2. Let X be the real Grassmannian , with m 2, n 3. Then we have

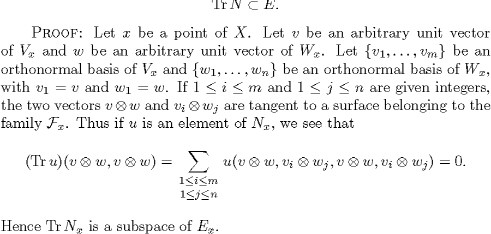
PROPOSITION 7.3. Let h be a section of E over the real Grassmannian X = with m 2 and n 3. If the restriction of h to an arbitrary submanifold of X belonging to the family is a Lie derivative of the metric of then h vanishes.

The infinitesimal rigidity of the complex quadric given by Theorem 6.45, implies that the family Fpossesses property (III) of 8, Chapter II; therefore we have

THEOREM 7.4. The real Grassmannian X = with m, n 2 and m + n 5, is infinitesimally rigid.

THEOREM 7.5. Let h be a symmetric 2-form on the real Grassmannian X = , with m, n 3. If h belongs to L(F), then h is a Lie derivative of the metric of X.

In Chapter X, we shall show that the Grassmannian is not infinitesimally rigid; on the other hand, Theorem 10.20 tells us that the Grassmannian is infinitesimally rigid

PROPOSITION 7.7. Let h be a section of EY over the real Grassman-nian with m 2 and n 3. If the restriction of h to an arbitrary submanifold of Y belonging to the family is a Lie derivative of the metric of Y , then h vanishes.

PROOF: The symmetric 2-form on X = is even and is a section of the vector bundle E over X. If h is an element of , then the form belongs to The desired result is a consequence of Proposition 7.3.

We remark that the preceding proposition actually requires only Theorem 6.43 rather than Theorem 6.46, whose proof relies upon both Theorems 6.43 and 6.44 and which is needed for the case of an arbitrary symmetric 2-form considered in Proposition 7.3.

THEOREM 7.8. The real Grassmannian X = with m, n 2 and is rigid in the sense of Guillemin.

PROOF: Since a submanifold Z of X belonging to the family is isometric to the complex quadric of dimension n endowed with the metric we know that the sequence (1.24) for Z is exact. The desired result is given by Proposition 2.46,(ii).

THEOREM 7.11. Let m, n 2 be given integers, with A 1-form on the real Grassmannian Y = satisfies the Guillemin condition if and only if it is exact.

THEOREM 7.12. Let m, n 2 be given integers, with m + n 5. A 1-form on the real Grassmannian X = satisfies the zero-energy condition if and only if it is exact.

THEOREM 7.12 is given by Theorem 3 of [20]. In Chapter X, we shall show that a 1-form on the Grassmannian satisfies the zero-energy condition if and only if it is exact (see Theorem 10.21).

2. The real Grassmannians

Let F be a real vector space of dimension m + n, where m, n 1, endowed with a positive definite scalar product. We consider the real Grassmannians and endowed with the Riemannian metrics induced by the scalar product of F, which are defined in 1, Chapter IV. There we also saw that the natural mapping

LEMMA 7.13. Let n 2 be a given integer. Let F be a real vector space of dimension 2n + 2 endowed with a positive definite scalar product and let U be a subspace of F of dimension 2n. If is an even symmetric p-form on then the symmetric p-form on is even.

Let be a maximal flat totally geodesic torus of Y ; then we easily

p1see that is a maximal flat totally geodesic torus of X. Let be arbitrary parallel vector fields on they induce parallel vector fields on determined by

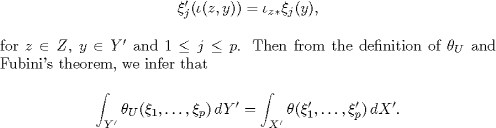
From this equality, we deduce the following result:

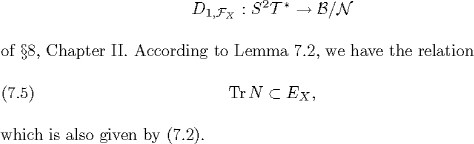
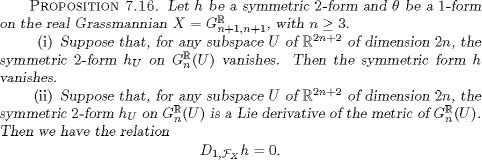
Let n be an integer 2, and let U be a real vector space of dimension 2n endowed with a positive definite scalar product. According to an observation made in 1, Chapter IV, if all even functions on GR n,n satisfying the Guillemin condition vanish, then the analogous result is also true for the Grassmannian GRn (U); moreover if all even symmetric 2-forms (resp. 1-forms) on GR n,n satisfying the Guillemin condition are Lie derivatives of the metric (resp. are exact), then the analogous result is also true for the Grassmannian GRn (U). We shall use these remarks in the course of the proofs of the next three propositions.

PROPOSITION 7.17. For n 2, the maximal flat Radon transform for functions on the symmetric space G^Rn,n is injective.

PROOF: We proceed by induction on n 2. Proposition 4.4 tells us that the desired result is true for n = 2. Next, let n 2 be a given integer and suppose that the maximal flat Radon transform for functions on the symmetric space G^Rn,n is injective. Let f be an even real-valued function on X = GRn +1,n+1 satisfying the Guillemin condition. Let U be an arbitrary subspace of R2n+2 of dimension 2n. According to Lemmas 7.13 and 7.14, the function fU on GRn (U) is even and satisfies the Guillemin condition. From Lemma 4.5 and our induction hypothesis, we infer that the function fU vanishes. Then by Proposition 7.15, we know that f vanishes. According to Lemma 4.5, this argument gives us the desired result for the space X.

The preceding proposition is also given by Theorem 2.24.

PROPOSITION 7.18. Let n be an integer 3 and suppose that all even symmetric 2-forms on GR n,n satisfying the Guillemin condition are Lie derivatives of the metric. Then an even symmetric 2-form on X = GRn +1,n+1 satisfying the Guillemin condition is a Lie derivative of the metric.

PROOF: Let k be an even symmetric 2-form on X satisfying the Guillemin condition. According to the decomposition (1.11), we may decompose k as

PROPOSITION 7.19. Let n be an integer 3 and suppose that all even 1-forms on GR n,n satisfying the Guillemin condition are exact. Then an even 1-form on X = GRn +1,n+1 satisfying the Guillemin condition is exact.

PROOF: Let be an even 1-form on X satisfying the Guillemin condition. Let U be an arbitrary subspace of R2n+2 of dimension 2n and consider the Grassmannian Y = GRn (U). According to Lemmas 7.13 and 7.14 and our hypothesis, the 1-form U on Y is closed. Therefore by Proposition 7.15,(iii), we know that the restriction of dto an arbitrary subman-ifold of X belonging to the family FX vanishes. Then Lemma 7.6 tells us that d= 0. Since the cohomology group H1(X,R) vanishes, the form is exact.

The following theorem is a direct consequence of Propositions 2.18 and 7.18.

THEOREM 7.20. If the symmetric space GRn,n, with n 3, is rigid in the sense of Guillemin, then so is the space G

Rn +1,n+1.

The following proposition is a direct consequence of Propositions 2.20 and 7.19.

PROPOSITION 7.21. Let n be an integer 3 and suppose that all 1-forms on GRn,n satisfying the Guillemin condition are exact. Then a 1-form on X = G

Rn +1,n+1 satisfying the Guillemin condition is exact.

According to Proposition 4.3, the symmetric space G

R2 ,2 is isometric to the product RP2 × RP². In Chapter X, we shall show that this space is not rigid in the sense of Guillemin (Theorem 10.5) and that there exist 1-forms on this space which satisfy the Guillemin condition and which are not exact (Theorem 10.6).