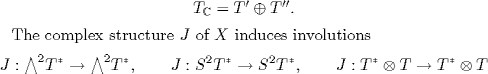CHAPTER I

SYMMETRIC SPACES AND EINSTEIN MANIFOLDS

1. Riemannian manifolds

Let E and F be vector bundles over X endowed with scalar products and D : E F be a differential operator of order k. We consider the scalar products on (E) and (F), defined in terms of these scalar products on E and F and the Riemannian measure of X, and the formal adjoint , which is a differential operator of order k. If D is elliptic and X is compact, then D(E) is a closed subspace of (F) and we have the orthogonal decomposition

LEMMA 1.1. Let Y be a totally geodesic submanifold of the Rieman-nian manifold (X, g). Let i : Y X be the natural imbedding and be the Riemannian metric on Y induced by g. Let be a vector field on X. If is the vector field on Y whose value at x Y is equal to the orthogonal projection of onto the subspace T_Y,x of T_x, then we have

Let be a vector field on X. According to the second Bianchi identity and the relation (1.4), we see that

If the scalar curvature r(g) of (X, g) is constant and equal to and if is a conformal Killing vector field, then by (1.16) we see that the real-valued function f =−(2/n) dsatisfying fg is a solution of the equation

If X is compact, we know that the eigenvalues of the Laplacian acting on C(X) are 0; hence from the previous observation, we obtain the following result due to Lichnerowicz [43, 83]:

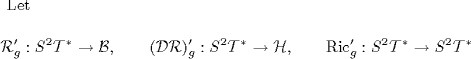
be the linear differential operators, which are the linearizations along g of the non-linear operators h R(h), h (DR)(h) and h Ric(h), respectively, where h is a Riemannian metric on X. Let h be a section of

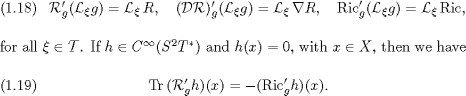
is equal .

The following result is given by Proposition 4.1 of [13].

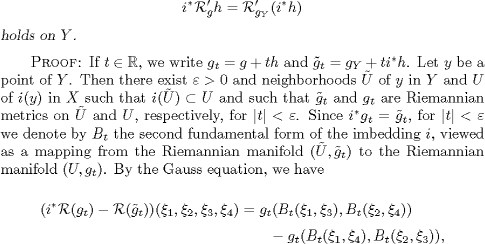
for all According to our hypothesis, we have B₀ = 0; thus if we differentiate both sides of the above equation with respect to t, at t = 0, we obtain

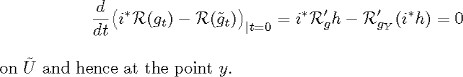
2. Einstein manifolds

We say that the Riemannian manifold (X, g) is an Einstein manifold if there is a real number such that Ric = g. In this section, we suppose that g is an Einstein metric, i.e., that there is a real number such that Ric = the scalar curvature r(g) of (X, g) is constant and equal to . By (1.29), we have

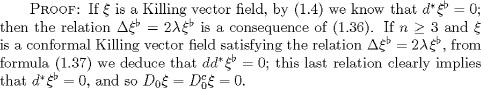
PROOF: Let h be a section of over X. If x X and h(x) = 0, then by (1.20) and (1.21) we have

If is a vector field on X, then we know that = 0; on the other hand, by the last relation of (1.18), we know that (1.38) holds. If x X, by the surjectivity of (D0) we know that there exists a vector field on X such that The commutativity of the diagram (1.40) is now a consequence of the previous observations.

The proof of Lemma 1.9 can be found in [3, 7]. The following lemma is a generalization of Proposition 3.2 of [22].

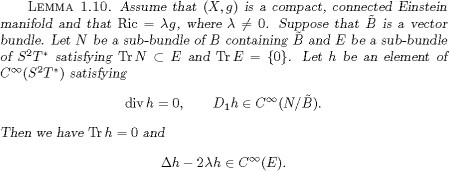
(see also Koiso [41]). By definition, the space E(X) is contained in an eigenspace of the Lichnerowicz Laplacian , which is an elliptic operator, and is therefore finite-dimensional.

According to Lemma 1.7, when is a vector bundle, we may take N = and E = {0} in Lemma 1.10; from the latter lemma and the relation between the space H(X) and the cohomology of the sequence (1.24), we obtain the following result:

3. Symmetric spaces

We say that the Riemannian manifold (X, g) is a locally symmetric space if R = 0. According to Lemma 1.4, if the equality

holds, then the manifold (X, g) is locally symmetric. Throughout this section, we shall suppose that the manifold (X, g) is a connected locally symmetric space. Since the set of local isometries of X acts transitively on X, we see that is a vector bundle. According to [13], the infinitesimal orbit of the curvature is equal to and so we have:

LEMMA 1.13. Suppose that (X, g) is a connected locally symmetric space. Then is a vector bundle equal to the infinitesimal orbit of the curvature

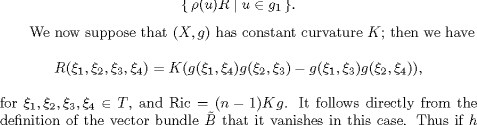
If the dimension of X is 3, in 1 we saw that TrB = , and so we obtain the inequalities

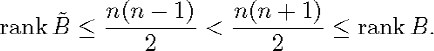
Thus we see that, if the dimension of X is 2, the vector bundle is always non-zero.

Let Y be a totally geodesic submanifold of X. Let i : Y X be the natural imbedding and gY = be the Riemannian metric on Y induced by g. Then (Y, gY ) is a locally symmetric space; its Riemann curvature tensor RY is equal to the section of BY and the infinitesimal orbit of Y is equal to . For x Y , the diagram

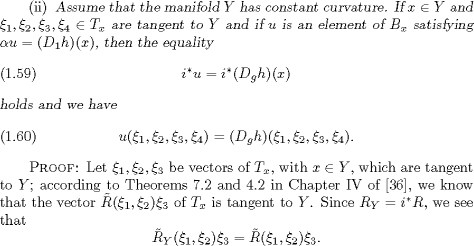
The equality (1.57) now follows from Proposition 1.3 and formula (1.21). Now suppose that Y is connected and let h be a section of . Let x be a point of Y and let u be an element of Bx satisfying u = (D1h)(x). First, suppose that h vanishes at the point x of Y . Then (Dgh)(x) is an element of Bx; by (1.25) and (1.58), we see that the vector u - (Dgh)(x) of Bx belongs to and that

LEMMA 1.15. Assume that (X, g) is a connected locally symmetric space. Let Y be a totally geodesic submanifold of X of constant curvature. Let h be a section of over X. Let x Y and u be an element of Bx such that (D1h)(x) = If the restriction of h to the submanifold Y is a Lie derivative of the metric on Y induced by g, then the restrictions of Dgh and u to the submanifold Y vanish.

PROOF: Let i : Y X be the natural imbedding and gY = be the Riemannian metric on Y induced by g. Assume that the restriction of h to the submanifold Y is equal to the Lie derivative of gY along a vector field on Y . Since Y has constant curvature, by (1.49) and (1.57) we have

From Proposition 1.14,(ii) and (1.59), we infer that iu = 0.

From Lemmas 1.1 and 1.15, we deduce the following result:

LEMMA 1.16. Assume that (X, g) is a connected locally symmetric space. Let Y , Z be totally geodesic submanifolds of X; suppose that Z is a submanifold of Y of constant curvature. Let be a section of over X. Let x Z and u be an element of Bx such that (D1h)(x) = If the restriction of h to the submanifold Y is a Lie derivative of the metric on Y induced by g, then the restriction of u to the submanifold Z vanishes.

We consider the third-order differential operator

the complex (1.63) to the cohomology of the sequence (1.24) induces an injective mapping from the cohomology group to the cohomology of the complex (1.24).

According to Theorem 7.3 of [13], if the equality (1.48) holds, a section h of satisfying D1h = 0 also satisfies the equation D2h = 0. Therefore if (1.48) is true, the complex (1.23) is exact and the two mappings considered above involving cohomology groups are isomorphisms. Moreover, if the equality (1.48) holds and X is simply-connected, the sequence (1.24) is exact; on the other hand, if the equality (1.48) holds and X is compact, the cohomology group ( is isomorphic to H(X).

THEOREM 1.18. Suppose that (X, g) is a connected locally symmetric space satisfying one of the following conditions:

(ii) (X, g) is a symmetric space of compact type.

Then the sequence (1.63) is exact. If the equality (1.48) holds, the sequence (1.24) is also exact.

We now suppose that (X, g) has constant curvature K; then the vector bundle vanishes and so the equality (1.48) holds. Thus the complex (1.50) is exact. If X is simply-connected, the sequence (1.51) is also exact. These two results were first proved by Calabi [8] (see also [2]); other direct proofs are given in [13, 6]. Furthermore if (X, g) is a compact surface of constant curvature K, from the equalities (1.53) and (1.54) we obtain the following proposition, whose first assertion is given by [2, p. 24].

PROPOSITION 1.19. Let (X, g) be a compact surface of constant curvature K.

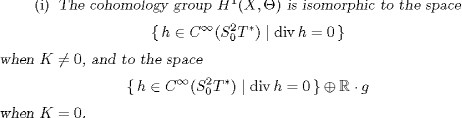
(ii) If K 0 and the cohomology group vanishes, then we have E(X) = {0}.

We now suppose that X is equal to the sphere (Sn, g0) of constant curvature 1, which is a symmetric space of compact type. We know that the sequences (1.24) and (1.51) are exact and that the cohomology groups and H(X) vanish. When X is equal to the sphere (S2, g0), according to Proposition 1.19,(i) and the decomposition (1.12) we see that

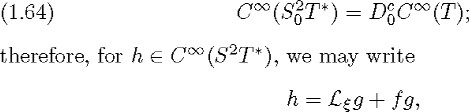
where is a vector field and f is a real-valued function on X = S2. Moreover, by Proposition 1.19,(ii), we have E(X) = {0} when X = S

2.

If (X, g) is a compact manifold with positive constant curvature, then its universal covering manifold is isometric to where is a positive real number. Thus from Theorem 1.18 and the above results, we obtain the following:

PROPOSITION 1.20. Let (X, g) is a compact manifold with positive constant curvature. Then cohomology group and the space H(X) vanish, and the sequence (1.51) is exact.

We now suppose that (X, g) is a symmetric space of compact type. Then there is a Riemannian symmetric pair (G,K) of compact type, where G is a compact, connected semi-simple Lie group and K is a closed subgroup of G, such that the space X is isometric to the homogeneous space G/K endowed with a G-invariant metric. We identify X with G/K, and let x0 be the point of X corresponding to the coset of the identity element of G in G/K. If and are the Lie algebras of G and K, respectively, we consider the Cartan decomposition corresponding to the Riemannian symmetric pair (G,K), where p0 is a subspace of . We identify p0 with the tangent space to X at the point x0. If B is the Killing form of the Lie algebra , the restriction of -B to induces a G-invariant Riemannian metric on X. According to Theorem 7.73 of [6], we know that

LEMMA 1.21. Let (X, g) be an irreducible symmetric space of compact type. Then g is an Einstein metric and there is a positive real number such that Ric = moreover, the metric g0 induced by the Killing form of is equal to

In [41] and [42], Koiso proved the following:

Theorem 1.22. Let X be an irreducible symmetric space of compact type whose universal covering manifold is not equal to one of the following:

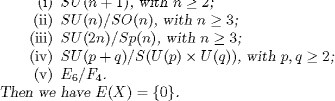
Some of the methods used by Koiso to prove Theorem 1.22 will be described in Chapter II; in fact, we shall give an outline of the proof of this theorem for an irreducible symmetric space X which is not equal to a simple Lie group. According to the remarks preceding Theorem 1.18, from Lemma 1.12 and Theorem 1.22 we deduce:

THEOREM 1.23. Let X be an irreducible symmetric space of compact type whose universal covering manifold is not equal to one of the spaces (i)–(v) of Theorem 1.22. Then the sequence (1.24) is exact.

In [13] and [10], the equality (1.48) is proved for the complex projective space with n 2, and the complex quadric of dimension 3 (see Propositions 3.32 and 5.14). Thus from Theorem 1.18, without the use of the space of infinitesimal Einstein deformations, we obtain the exactness of the sequence (1.24) when X is an irreducible symmetric space of compact type equal either to a sphere, to a real or complex projective space, or to the complex quadric of dimension 3. Theorem 1.23 also gives us the exactness of the sequence (1.24) for these irreducible symmetric spaces other than the complex quadric of dimension 4. In fact, we conjecture that the equality (1.48) holds for any irreducible symmetric space.

4. Complex manifolds

In this section, we suppose that X is a complex manifold endowed with a Hermitian metric g. We consider the sub-bundles Tand Tof TC of complex vector fields of type (1, 0) and (0, 1), respectively; then we have the decomposition