CHAPTER II

RADON TRANSFORMS ON SYMMETRIC SPACES

1. Outline

In this chapter, we introduce the Radon transforms for functions and symmetric forms on a symmetric space (X, g) of compact type, namely the X-ray transform and the maximal flat transform. In we present results concerning harmonic analysis on homogeneous spaces and use them to study these Radon transforms in and to describe properties of certain spaces of symmetric forms in The notions of rigidity in the sense of Guillemin and of infinitesimal rigidity of the space X are introduced in in this section, we also state the fundamental result of Guillemin [35] concerning isospectral deformations of the metric g of X (Theorem 2.14). In 4, we present Grinberg’s theorem concerning the injectivity of the maximal flat Radon transform for functions on X; when the space (X, g) is irreducible, from this result we infer that, if the space X is rigid in the sense of Guillemin, it is necessarily equal to its adjoint space. In criteria for the rigidity of the space X are given in terms of harmonic analysis. Some lemmas concerning irreducible G-modules, where G is a compact semi-simple Lie group, proved in are used in our study of symmetric forms on an irreducible symmetric space presented in . Results concerning the space of infinitesimal Einstein deformations of an irreducible symmetric space can be found in Our criteria for the infinitesimal rigidity or the rigidity in the sense of Guillemin of an irreducible symmetric space are given in

Homogeneous vector bundles and harmonic analysis

Let (X, g) be a Riemannian manifold which may be written as a homogeneous space G/K, where G is a compact Lie group and K is a closed subgroup of G. We assume that the group G acts by isometries on the Riemannian manifold X. If F is a homogeneous vector bundle over X, then the space (F) is a G-module.

Let F be a complex homogeneous vector bundle over X endowed with a Hermitian scalar product. We endow the space of sections of F over X with the Hermitian scalar product obtained from the scalar product on F and the Riemannian measure dX of X. If the vector bundle F is unitary in the sense of [56, 2.4], then the space (F) is a unitary G-module. Let x0 be the point of X corresponding to the coset of the identity element of G. The action of G on the fiber F0 of F at the point x0 of X induces a representation of K on F0. Then F is isomorphic to the homogeneous vector bundle and we shall identify these two homogeneous vector

Let and be the Lie algebras of G and K, respectively. In this section, we henceforth suppose that G/K is a reductive homogeneous space; this means that there is an Ad(K)-invariant complement of in This assumption always holds when the compact group G is connected and semi-simple and (G,K) is a Riemannian symmetric pair of compact type. Let F1, F2, F3 be complex homogeneous vector bundles over X endowed with Hermitian scalar products. Assume that these vector bundles are unitary.

PROOF: First, suppose that assertion (ii) holds. Then according to Proposition 2.2,(i) the subspace KerQ2 is equal to the closure of

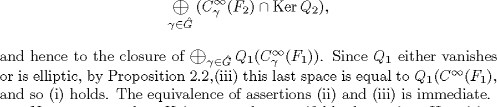
Now suppose that X is a complex manifold, that g is a Hermitian metric and that the group G acts by holomorphic isometries on X. Then the vector bundles and are homogeneous sub-bundles of TC, while the vector bundles and are homogeneous sub-bundles of The isomorphisms of vector bundles (1.70) are G-equivariant. Therefore for all G, the isomorphism of vector bundles : induces isomor-phisms of G-modules

3. The Guillemin and zero-energy conditions

Let (X, g) be a Riemannian manifold. For p 0, we consider the symmetrized covariant derivative

Definition 2.5. We say that a symmetric p-form u on X satisfies the zero-energy condition if, for every closed geodesi of X, the integral of u over vanishes.

Let Y be a totally geodesic submanifold of X; clearly, if is a symmetric p-form on X satisfying the zero-energy condition, then the restriction of u to Y also satisfies the zero-energy condition. From Lemma 2.4, we obtain the following result:

LEMMA 2.6. If u is a symmetric p-form on X, then the symmetric (p + 1)-form D^pu satisfies the zero-energy condition. A symmetric 2-form on X, which is equal to a Lie derivative of the metric g, satisfies the zero-energy condition.

DEFINITION 2.7. We say that the Riemannian metric g on X is a CL-metric if all its geodesics are periodic and have the same length L.

If g is a CL-metric, we say that X is a CL-manifold; then the geodesic flow on the unit tangent bundle of (X, g) is periodic with least period L.

The following proposition is due to Michel (Proposition 2.2.4 of [45]; see also Proposition 5.86 of [5]).

PROPOSITION 2.8. Let be a one-parameter family of CL-metrics on X, for with g0 = g. Then the infinitesimal deformation h = of {gt} satisfies the zero-energy condition.

From the previous equalities, we infer that

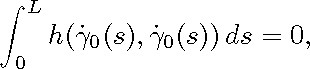
and so h satisfies the zero-energy condition.

DEFINITION 2.9. We say that a symmetric p-form u on a compact locally symmetric space X satisfies the Guillemin condition if, for every maximal flat totally geodesic torus Z contained in X and for all unitary parallel vector fields on Z, the integral

vanishes.

From Lemma 2.4, we obtain:

LEMMA 2.10. Let X be a compact locally symmetric space. If u is a symmetric p-form on X, then the symmetric (p+1)-form D^pu satisfies the Guillemin condition. If is a vector field on X, the symmetric 2-form on X satisfies the Guillemin condition.

Thus every exact one-form on a compact locally symmetric space satisfies the Guillemin and zero-energy conditions.

LEMMA 2.11. Let X be a flat torus. A symmetric p-form on X satisfying the zero-energy condition also satisfies the Guillemin condition.

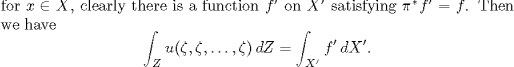
If u satisfies the zero-energy condition, then the functions f and vanish, and so, by the preceding formula, satisfies the Guillemin condition.

If (X, g) is a compact locally symmetric space, according to Lemma 2.11 a symmetric p-form on X satisfying the zero-energy condition also satisfies the Guillemin condition.

DEFINITION 2.12. We say that a compact locally symmetric space X is rigid in the sense of Guillemin (resp. infinitesimally rigid) if the only symmetric 2-forms on X satisfying the Guillemin (resp. the zero-energy) condition are the Lie derivatives of the metric g.

If X is a compact locally symmetric space X and p 0 is an integer, we consider the space of all sections of satisfying the zero-energy condition. According to Lemma 2.6, we have the inclusion

By formula (1.4), we see that the infinitesimal rigidity of the compact locally symmetric space X is equivalent to the equality On the other hand, the equality means that every differential form of degree 1 on X satisfying the zero-energy condition is exact.

PROPOSITION 2.13. Let X be a compact locally symmetric space. Then the following assertions are equivalent:

(i) Every symmetric 2-form h on X, which satisfies the Guillemin (resp. the zero-energy) condition and the relation div h = 0, vanishes.

(ii) The space X is rigid in the sense of Guillemin (resp. is infinitesimally rigid).

PROOF: First assume that assertion (i) holds. Let h be a symmetric 2-form on X satisfying the Guillemin (resp. the zero-energy) condition. According to the decomposition (1.11), we may write

where is an element of satisfying div h0 = 0 and Clearly, by Lemma 2.10 (resp. Lemma 2.6), the symmetric 2-form h0 also satisfies the Guillemin (resp. the zero-energy) condition; our assumption implies that vanishes, and so h is a Lie derivative of the metric. Therefore (ii) is true. According to the decomposition (1.11), we see that assertion (i) is a direct consequence of (ii).

We now assume that (X, g) is a symmetric space of compact type. If the space X is rigid in the sense of Guillemin, it is also infinitesimally rigid. If X is a space of rank one, the closed geodesics of X are the maximal flat totally geodesic tori of X, and so the notions of Guillemin rigidity and infinitesimal rigidity for X are equivalent.

Consider a family of Riemannian metrics {gt} on X, for , with

tg0 = g. We say that {gt} is an isospectral deformation of g if the spectrum Spec(X, gt) of the metric gt is equal to Spec(X, g), for all < . We say that the space (X, g) is infinitesimally spectrally rigid (i.e., spectrally rigid to first-order) if, for every such isospectral deformation {gt} of g, there is a one-parameter family of diffeomorphisms t of X such that gt to first-order in t at t = 0, or equivalently if the infinitesimal deformation d is a Lie derivative of the metric g.

In [35], Guillemin proved the following result:

THEOREM 2.14. A symmetric 2-form on a symmetric space (X, g) of compact type, which is equal to the infinitesimal deformation of an isospectral deformation of g, satisfies the Guillemin condition.

This theorem leads us to Guillemin’s criterion for the infinitesimal spectral rigidity of a symmetric space of compact type which may be expressed as follows:

Theorem 2.15. If a symmetric space of compact type is rigid in the sense of Guillemin, it is infinitesimally spectrally rigid.

4. Radon transforms

Let (X, g) be a symmetric space of compact type. Then there is a Riemannian symmetric pair (G,K) of compact type, where G is a compact, connected semi-simple Lie group and K is a closed subgroup of G such that the space X is isometric to the homogeneous space G/K endowed with a G-invariant metric. We identify X with G/K, and let x0 be the point of X corresponding to the coset of the identity element of G in G/K. Since the maximal flat totally geodesic tori of X are conjugate under the action of G on X, the space of all such tori is a homogeneous space of G. We also consider the set of all closed geodesics of X; when the rank of X is equal to one, then is equal to .

A Radon transform for functions on X assigns to a function on X its integrals over a class of totally geodesic submanifolds of X of a fixed dimension. Here we shall consider two such Radon transforms, the maximal flat Radon transform and the X-ray transform.

The maximal flat Radon transform for functions on X assigns to a real-valued function f on X the function f on , whose value at a torus Z is the integral

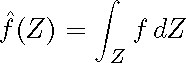
of f over Z. Clearly this transform is injective if every function on X satisfying the Guillemin condition vanishes. The X-ray transform for functions on X assigns to a real-valued function f on X the function on , whose value at a closed geodesic is the integral

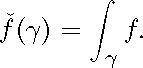
Clearly this transform is injective if every function on X satisfying the zero-energy condition vanishes. If the rank of X is equal to one, the maximal flat Radon transform for functions on X coincides with the X-ray transform for functions on X.

Let f be a real-valued function on X. If Z is a torus belonging to and if is a unitary parallel vector field on Z, then we see that

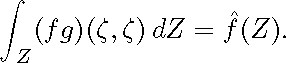
On the other hand, if is a closed geodesic of X, we have

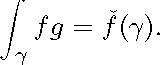
Thus the maximal flat Radon (resp. the X-ray) transform of f vanishes if and only if the symmetric 2-form fg satisfies the Guillemin (resp. the zero-energy) condition.

If X is an irreducible symmetric space of compact type, we recall that g is an Einstein metric and that Ric = g, where is a positive real number; moreover, the space E(X) of infinitesimal Einstein deformations of the metric g is a G-submodule of

PROPOSITIOn 2.16. Let X be an irreducible symmetric space of compact type, which is not isometric to a sphere. If X is rigid in the sense of Guillemin (resp. is infinitesimally rigid), then the maximal flat Radon (resp. the X-ray) transform for functions on X is injective.

PROOF: Assume that X is rigid in the sense of Guillemin (resp. is infinitesimally rigid). Let f be real-valued function on the Einstein manifold X; suppose that the function (resp. the function vanishes. Then the symmetric 2-form fg on X satisfies the Guillemin (resp. the zero-energy) condition. Therefore we may write where is a vector field on X. According to Proposition 1.6, the function f vanishes, and so the corresponding Radon transform for functions is injective.

Let be a finite group of isometries of X of order q. If F is a vector bundle equal either to a sub-bundle of TC or to a sub-bundle of invariant under the group , we denote by )the space consisting of all -invariant sections of F; if the vector bundle F is also invariant under the group G and if the isometries of commute with the action of G, then is a G-submodule of If F is the trivial complex line bundle, we consider the G-submodule of -invariant functions on X.

We suppose that the group acts without fixed points. Then the quotient is a manifold and the natural projection : X Y is a covering projection. Thus the metric g induces a Riemannian metric on Y such at gY = g. Clearly the space Y is locally symmetric.

A symmetric p-form on X is invariant under the group if and only if there is a symmetric p-form on Y such that The projection induces an isomorphism

If X is an irreducible symmetric space, then X and Y are Einstein manifolds; according to the definition of the spaces E(X) and E(Y ) of infinitesimal Einstein deformations, we see that the projection and the isomorphism (2.5) induce an isomorphism

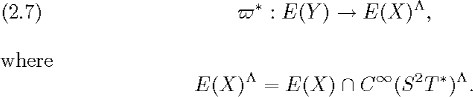
Throughout the remainder of this section, we also suppose that the isometries of commute with the action of G on X; then Y is a homogeneous space of G. Assume furthermore that there is a subgroup of G containing K and a G-equivariant diffeomorphism which have the following properties:

(i) (G,) is a Riemannian symmetric pair;

(ii) when we identify X with G/K, the projection is equal to the natural projection .

Under these conditions, the space (Y, gY ) is isometric to the symmetric space of compact type endowed with a G-invariant metric.

holds for all symmetric p-forms on Y .

From the above observations, we deduce

From the above observations, we deduce the following:

LEMMA 2.17. Suppose that the quotient is a symmetric space. Then a symmetric p-form u on Y satisfies the Guillemin (resp. the zero-energy) condition if and only if the symmetric p-form u on X, which is invariant under the group , satisfies the Guillemin (resp. the zero-energy) condition.

By Lemma 2.17, we see that the maximal flat Radon (resp. the X-ray) transform for functions on Y is injective if and only if the restriction of the the maximal flat Radon (resp. the X-ray) transform for functions on X to the space is injective. From Lemma 2.17 and the equality (2.6), we deduce the following three results:

PROPOSITION 2.18. Suppose that the quotient is a symmetric space. Then the following assertions are equivalent:

(i) Every symmetric 2-form on the space X, which is invariant under the group and satisfies the Guillemin condition, is a Lie derivative of the metric.

(ii) The space Y is rigid in the sense of Guillemin.

PROPOSITION 2.19. Suppose that the quotient is a symmetric space. Then the following assertions are equivalent:

(i) Every symmetric 2-form on the space X, which is invariant under the group and satisfies the zero-energy condition, is a Lie derivative of the metric.

(ii) The space Y is infinitesimally rigid.

PROPOSITION 2.20. Suppose that the quotient is a symmetric space. Then the following assertions are equivalent:

(i) Every differential form of degree 1 on the space X, which is invariant under the group and satisfies the Guillemin (resp. the zero-energy) condition, is exact.

(ii) Every differential form of degree 1 on the space Y , which satisfies the Guillemin (resp. the zero-energy) condition, is exact.

induced by (2.5), is an isomorphism of G-modules.

The following proposition is a consequence of Lemma 2.17.

PROPOSITION 2.21. Suppose that the quotient is a symmetric space. Let F be a sub-bundle of SpTinvariant under the groups G and , and let FY be the G-invariant sub-bundle of induced by F. Then the following assertions are equivalent:

(i) Any section of the vector bundle F over the space X, which is invariant under the group and satisfies the Guillemin (resp. the zero-energy) condition, vanishes.

(ii) Any section of the vector bundle FY over the space Y , which satisfies the Guillemin (resp. the zero-energy) condition, vanishes.

Let Z be a maximal flat totally geodesic torus of X. Since preserves Z, if f is an odd function on X, we see that the integral of f over Z vanishes. Therefore the odd functions on X satisfy the Guillemin condition, and so belong to the kernel of the maximal flat Radon transform for functions.

PROPOSITION 2.22. We suppose that the group is equal to the group {id, } of order 2, where is an involutive isometry of X, and that the quotient is a symmetric space. Then an odd symmetric p-form on X satisfies the Guillemin condition, and the maximal flat Radon transform for functions on X is not injective. Moreover, the space X is not rigid in the sense of Guillemin.

PROOF: Let u be an odd symmetric p-form on X and let Z be a maximal flat totally geodesic torus of X. If is a parallel vector field on Z, then the function ( on Z is odd, that is,

for all hence its integral over Z vanishes. We now construct an odd symmetric 2-form on X which is not a Lie derivative of the metric. Let be a point of X and U be a open neighborhood of x for which . By Lemma 1.13 and remarks made in , Chapter I, we know that the infinitesimal orbit of the curvature Bis a vector bundle and that the quotient bundle B/Bis non-zero. According to 1, Chapter I, the morphism (D1) : S2TS2TB/Bis surjective; hence we may choose a symmetric 2-form h on X whose support is contained in U and which satisfies (D1h)(x) = 0. We know that h is not a Lie derivative of the metric on any neighborhood of x. The symmetric 2-form h= h - h on X is odd and its restriction to U is equal to h. Hence the form hsatisfies the Guillemin condition, and so the space X is not rigid in the sense of Guillemin.

In Chapter III, we shall prove that the X-ray transform for functions on the sphere Sn, with is injective on the space of all even functions (see Proposition 3.17). Clearly, this result is equivalent to assertion (i) of the following theorem. By Lemma 2.17, we know that assertions (i) and (ii) of this theorem are equivalent. We point out that assertion (i) of this theorem in the case of the 2-sphere S2 is a classic result due to Funk.

THEOREM 2.23. (i) The kernel of the X-ray transform for functions on the sphere (Sn, g0), with n 2, is equal to the space of all odd functions on Sn.

(ii) The X-ray transform for functions on the real projective space with n 2, is injective.

The adjoint space of the symmetric space X is the symmetric space which admits X as a Riemannian covering and is itself not a Riemannian covering of another symmetric space. For example, the adjoint space of the n-sphere Sn, with n 2, is the real projective space

In [34], Grinberg generalized Theorem 2.23 and proved the following:

THEOREM 2.24. The maximal flat Radon transform for functions on a symmetric space X of compact type is injective if and only if X is equal to its adjoint space.

By Proposition 2.22, the sphere is not infinitesimally rigid. Hence from Proposition 2.16 and Theorem 2.24, we obtain the following necessary condition for Guillemin rigidity:

THEOREM 2.25. Let X be an irreducible symmetric space of compact type. If X is rigid in the sense of Guillemin, then X is equal to its adjoint space.

In Chapter III, we shall show that the X-ray transform for functions on a flat torus of dimension > 1 is injective; this result is due to Michel [46] (see Proposition 3.5). If the symmetric space X is of rank q, each point of X is contained in a totally geodesic flat torus of dimension q of X (see Theorem 6.2 in Chapter V of [36]). Thus from the injectivity of the X-ray transform for functions on a flat torus, we deduce the following:

PROPOSITION 2.26. The X-ray transform for functions on a symmetric space X of compact type of rank > 1 is injective.

We now extend the definitions of the maximal flat Radon transform and the X-ray transform to symmetric p-forms. Let L be the vector bundle over whose fiber at a point Z is the space of all parallel vector fields on the flat torus Z. This vector bundle is a homogeneous G-bundle over and its rank is equal to the rank of the symmetric space X. We consider the p-th symmetric product of the dual Lof L. The space of all symmetric p-forms on X and the space ( of all sections of ove are G-modules. The maximal flat Radon transform for symmetric p-forms on X is the morphism of G-modules

which assigns to a symmetric p-form u on X the section of who se value at the point Z is determined by

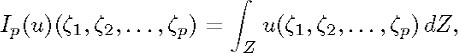
where 1, 2, . . . , p are elements of LZ. The kernel Np of this mapping Ip is the G-submodule of equal to the space consisting of all symmetric p-forms on X which satisfy the Guillemin condition. The com-plexification of the space shall be viewed as the G-submodule of equal to the kernel of the morphism of G-modules

induced by the mapping Ip. The mapping I0 coincides with the maximal flat Radon transform for functions defined above, while the mapping I2 was introduced in [23].

The X-ray transform for symmetric p-forms on X is the linear mapping sending an element (SpT) into the real-valued function on pu Cu whose value at the closed geodesic is the integral

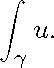
The kernel of this mapping is equal to the space of all symmetric p-forms on X satisfying the zero-energy condition. Then according to Lemma 2.11, we have

for G, is a morphism of G-modules. The complexification of the space shall be viewed as the G-submodule

of consisting of all complex symmetric p-forms on X which satisfy the zero-energy condition.

When the rank of X is equal to one, the vector bundle L is a line bundle; in this case, the X-ray transform for symmetric p-forms, which may be viewed as a morphism of G-modules

determines the maximal flat Radon transform for symmetric p-forms.

5. Radon transforms and harmonic analysis

Let 0 be the subset of consisting of those elements of for which the G-module is non-zero. It is well-known that, for 0, the G-module is irreducible (see Theorem 4.3 in Chapter V of [37]).

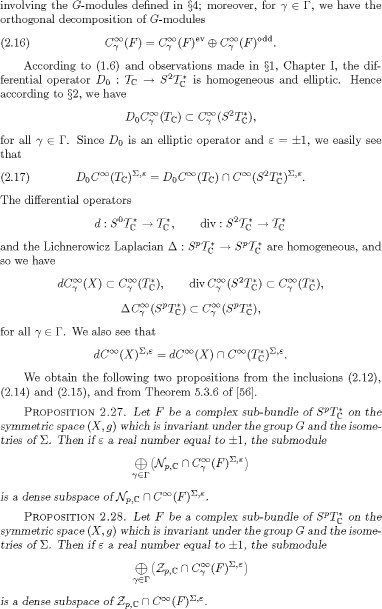
The following proposition is a direct consequence of Propositions 2.27 and 2.28.

PROPOSITION 2.29. Let (X, g) be a symmetric space of compact type. Let be a finite set of isometries of X which commute with the action of G on X and let be a real number equal to .

±(i) The restriction of the maximal flat Radon transform for functions on X to the space ^,is injective if and only if the equality

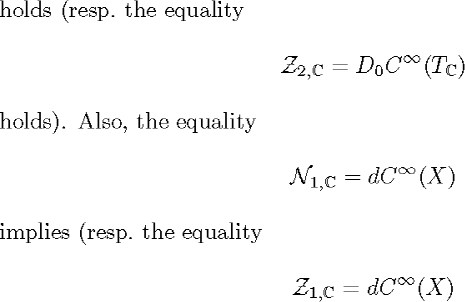
implies) that any differential form of degree 1 on X satisfying the Guillemin (resp. the zero-energy) condition is exact.

PROPOSITION 2.30. Let (X, g) be a symmetric space of compact type. Let be a finite set of isometries of X which commute with the action of G on X and let be a real number equal to .

PROOF: Since D0 is an elliptic homogeneous differential operator, the assertions of the proposition follow from the first inclusion of (2.15), the equality (2.17) and from Propositions 2.2,(iii), 2.27 and 2.28.

PROPOSITION 2.30 gives us the following criteria for the Guillemin rigidity and the infinitesimal rigidity of X, which are analogous to the criteria for the injectivity of the Radon transforms for functions on X obtained from Proposition 2.29:

PROPOSITION 2.31. Let (X, g) be a symmetric space of compact type.

(i) The space X is rigid in the sense of Guillemin if and only if

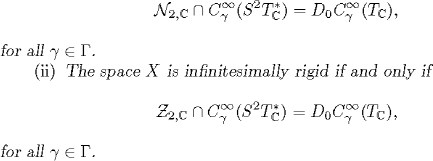
PROPOSITION 2.32. Let (X, g) be a symmetric space of compact type. Let be a finite set of isometries of X which commute with the action of G on X and let be a real number equal to .

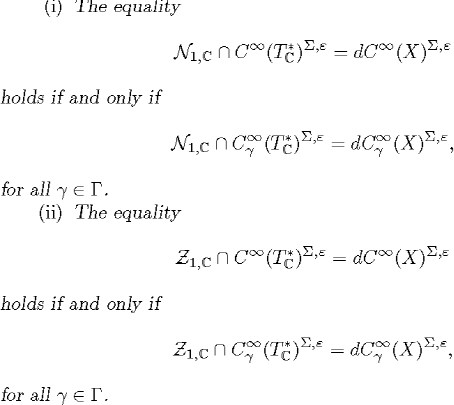
PROOF: Since the exterior differential operator d acting on is an elliptic homogeneous differential operator, the assertions of the proposition follow from (2.15) and Propositions 2.2,(iii), 2.27 and 2.28.

PROPOSITION 2.32 gives us the following criteria, which are analogous to the criteria for the Guillemin rigidity and the infinitesimal rigidity of X given by Proposition 2.31:

PROPOSITION 2.33. Let (X, g) be a symmetric space of compact type. The following assertions are equivalent:

(i) A differential form of degree 1 on the space X satisfies the Guil-lemin (resp. the zero-energy) condition if and only if it is exact.

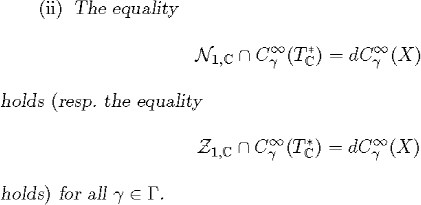
Suppose that is equal to a finite group of isometries of X which commute with the action of G and that is equal to +1. Assume that acts without fixed points and that the quotient space is a symmetric space; furthermore, assume that there is a subgroup of G containing K and a G-equivariant diffeomorphism satisfying properties (i) and (ii) o4. If the vector bundle F is a sub-bundle of which is invariant under , we consider the sub-bundle FY of determined by F; then for , the G-submodule

of G-modules.

We choose a Cartan subalgebra of the complexification g of the Lie algebra of G and fix a system of positive roots of g. Let p be an integer equal to 1 or 2 and consider the corresponding homogeneous differential operator We consider the following properties which the space X and the group might possess:

(Ap) Let be an arbitrary element of , and let u be an arbitrary highest weight vector of the G-module if the section u satisfies the Guillemin condition, then u belongs to ).

(Bp) Let be an arbitrary element of , and let u be an arbitrary highest weight vector of the G-module if the section u satisfies the zero-energy condition, then u belongs to ).

According to the relation (1.4) and Propositions 2.30 and 2.32, we see that in order to prove that the equality

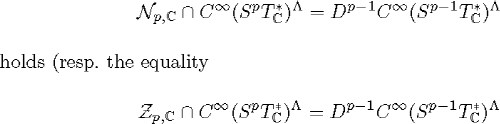
holds), it suffices to verify that X and possess property Ap (resp. property Bp).

Thus according to Proposition 2.18 (resp. Proposition 2.19) and the relation (1.4), we know that, if the space X and the group possess property A2 (resp. property B2), the space Y is rigid in the sense of Guillemin (resp. is infinitesimally rigid). On the other hand, according to Proposition 2.20, if the space X and the group possess property A1 (resp. property B1), then every differential form of degree 1 on the space Y , which satisfies the Guillemin (resp. the zero-energy) condition, is exact.

These methods for proving the rigidity of a symmetric space of compact type were first introduced in [14] in the case of the complex projective space (see 5, Chapter III). The analogous method for proving the injectivity of Radon transforms for functions described above was first used by Funk to prove Theorem 2.23 for the 2-sphere S2 and the real projective plane (see also Proposition 3.17); it was also applied by Grinberg in [31] to other projective spaces. The methods described above will be applied to the real Grassmannian of 2-planes in and to the complex quadric Qn of dimension n. In fact, they shall be used in Chapter VI to show that the real Grassmannian is rigid in the sense of Guillemin and that the complex quadric is infinitesimally rigid, and in 4, Chapter X to show that the real Grassmannian is infinitesimally rigid. Also the criterion for the exactness of a differential form of degree 1, which we have just described, shall be used in the case of the real projective plane in Chapter III, in the case of the complex quadric and of the real Grassmannian with n 3, in 11, Chapter VI, and in the case of the real Grassmannian in 4, Chapter X.

6. Lie algebras

Let g be a complex semi-simple Lie algebra. The Casimir element of operates by a scalar ( on an irreducible finite-dimensional g-module If g is simple, the Casimir element of acts on the irreducible g-module corresponding to the adjoint representation of g by the identity mapping, and so (see Theorem 3.11.2 of [55]).

LEMMA 2.34. Let be a complex semi-simple Lie algebra. Let V1 and V2 be irreducible finite-dimensional modules. Then the modules V1 and V2 are isomorphic if and only if c(V1) = c(V2).

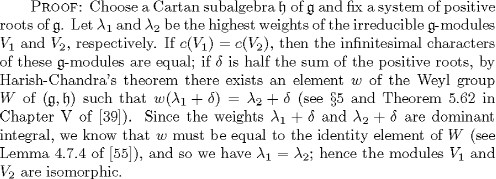
Let G be a compact connected, semi-simple Lie group, whose Lie algebra we denote by A complex G-module V can be viewed as a g0-module and so the Casimir element of operates on V ; if V is an irreducible G-module, the Casimir element of acts by the scalar c(V ) on V .

From Lemma 2.34, we obtain the following result:

LEMMA 2.35. Let G be a compact connected, semi-simple Lie group. Let V1 and V2 be irreducible complex G-modules. Then the G-modules V1 and V2 are isomorphic if and only if c(V1) = c(V2).

7. Irreducible symmetric spaces

We consider the symmetric space (X, g) of compact type of 4. We write X as the homogeneous space G/K, where G is a compact, connected semi-simple Lie group and K is a closed subgroup of G. We suppose that g is a G-invariant metric and that (G,K) is a Riemannian symmetric pair of compact type. We continue to denote by the dual of the group G. Let x0 be the point of X corresponding to the coset of the identity element of G. If and are the Lie algebras of G and K, respectively, we consider the Cartan decomposition corresponding to the Riemannian symmetric pair (G,K), where is a subspace of We identify with the tangent space to X at the point x0. If B is the Killing form of the Lie algebra of G, then the restriction of -B to induces a G-invariant Riemannian metric on X. The complexifications of and of are K-modules. We denote by Skp the k-th symmetric product of and by the K-submodule of S2p consisting of those elements of S2p of trace zero with respect to the Killing form of g. The isotropy group K acts on in fact, the K-modules and S2 x0 0TC,are isomorphic to the x0

K-modules and respectively. If X is an irreducible Hermitian symmetric space, then we have

If X is an irreducible symmetric space which is not Hermitian, then we have

The G-module

of all Killing vector fields on X is isomorphic to We identify its com-plexification with the G-module

of complex vector fields on X, which is isomorphic to We know that a Killing vector fiel on X satisfies the relation thus the subspaces g(KC) and dC(X) of C(TC) are orthogonal.

K) The Lichnerowicz Laplacian acting on is self-adjoint and its eigenvalues are non-negative real numbers. Since the Laplacian acting on SpTCis elliptic, the eigenspace

of the Laplacian corresponding to the eigenvalue is finite-dimensional. The Casimir element of acts by a scalar an irreducible G-module which is a representative of . According to [41, 5], the action of the Lichnerowicz Laplacian

corresponding to the metric on X on the G-module coincides with the action of the Casimir element of g0 on this G-module. Thus, fo we see that is an eigenspace of the Lichnerowicz Laplacian g0 with eigenvalue c. Since the operato acting on is elliptic and real-analytic, the elements of C) are real-analytic sections of If F is a complex sub-bundle of invariant under the group G, then the Laplacian preserves the space

We suppose throughout the remainder of this section that X is an irreducible symmetric space. According to Lemma 1.21, the metric g is a positive multiple of g0 and is an Einstein metric. In fact, by formula (1.65), we have Ric =, where is a positive real number, and = moreover, the Lichnerowicz Laplacian corresponding to the metric g is equal . Let F be a complex sub-bundle of invariant under the group from Lemma 2.35 and the above remarks concerning the Laplacia we infer that the G-submodule is equal to the eigenspace of acting on associated with the eigenval Moreover, by Proposition 2.1 and the preceding remark, for we see that, if the eigenspace

(Xfor al If is an element of , according to (2.12) (resp. to (2.14)), we know that belongs to (resp. to therefore so does . Since (resp. is a closed subspace of we see that also belongs to this subspace.

PROPOSITION 2.37. Let (X, g) be an irreducible symmetric space of compact type. Let E be a G-invariant sub-bundle of and let h be a symmetric 2-form on X. Assume that there is a real number ì such that

(i) If ì is not an eigenvalue of the Laplacian acting on then h is a section of E.

(ii) Assume that ì is an eigenvalue of the Laplacian acting on and suppose that h satisfies div h = 0 and Tr h = 0. Then we can write h = h1 +h2, where h1 is a section of and is a section of E satisfying

moreover, if h satisfies the Guillemin (resp. the zero-energy) condition, then we may require that h1 and h2 also satisfy the Guillemin (resp. the zero-energy) condition.

The desired result is a direct consequence of formulas (1.39) and (1.10).

We now further assume that X is of type I, i.e. is not equal to a simple Lie group (see [36, p. 439]). We may suppose that the Lie group G is simple; then the complexification g of the Lie algebra g0 is simple. Let 1 be the element of which is the equivalence class of the irreducible G-module g. We know that c1 = 1, and hence we have 1 = 2. This observation and the above remarks concerning the Lichnerowicz Laplacians, together with the Frobenius reciprocity theorem, give us the following result:

Since E(X)C is G-submodule of we know that E(X)C is equal to the direct sum of k copies of the irreducible G-module , where is the integer MultE(X)C; it follows that the G-module E(X) is isomorphic to the direct sum of k copies of g0. Moreover, we infer that the vanishing of the space dimC HomK implies that the space E(X) vanishes.

Since the G-module KC is isomorphic to g, we see that

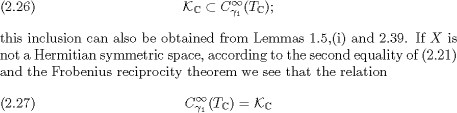
holds. If X is a Hermitian symmetric space, by (2.20) we see that is an irreducible G-module; since the decomposition of given by (1.69) is G-invariant, by (2.20) we obtain the orthogonal decompositions

whose components and are irreducible G-modules isomorphic to .

PROPOSITION 2.40. Let (X, g) be an irreducible symmetric space of compact type, which is not equal to a simple Lie group or to the sphere S2. Then the space E(X) of infinitesimal Einstein deformations of X is a Gmodule isomorphic to the direct sum of k copies of the irreducible G-module and its multiplicity k is equal to

Hence the equality (2.31) becomes

Since Mult is equal to one, the preceding equality together with the Frobenius reciprocity theorem gives us the first assertion of the proposition. The other assertions of the proposition then follow from the second equalities of (2.20) and (2.21).

In [42], Koiso also showed that the assertions of the previous proposition also hold when the irreducible space X is a simple Lie group. The following lemma is stated without proof by Koiso (see Lemma 5.5 of [42]); for the irreducible symmetric spaces

with p, q 2, we shall verify the results of this lemma in Chapter IV (see Lemma 4.1), Chapter V (see Lemma 5.15) and 3, Chapter VIII.

LEMMA 2.41. Let (X, g) be a simply-connected irreducible symmetric space of compact type which is not equal to a simple Lie group. If X is Hermitian, then the space Hom , is one-dimensional and if X is not Hermitian the space Hom, vanishes, unless X is one of the spaces appearing in the following table which gives the dimension of the space Hom,

The first two spaces X of this table are Hermitian, while the last three are not Hermitian.

Since the space is isometric to the sphere S

2, by Lemma 2.41 and the equalities (2.25) we know that the space E(X) vanishes when X is the sphere S2; we also proved this result directly in 3, Chapter I. Therefore from Proposition 2.40 and Lemma 2.41, we obtain the results of Theorem 1.22 when the space X of this theorem is not equal to a simple Lie group; moreover, when X is equal to one of the last four spaces of the table of Lemma 2.41, we see that the G-module E(X) is isomorphic to g0.

Thus according to Proposition 2.40 and Lemma 2.41, if X is an irreducible symmetric space of compact type, which is not equal to a simple Lie group, the space E(X) either vanishes or is isomorphic to the G-module .

From the relations (2.17), (2.18) and (2.26), we obtain the following result:

PROPOSITION 2.42. Let (X, g) be an irreducible symmetric space of compact type, which is not equal to a simple Lie group, and let be the element of which is the equivalence class of the irreducible G-module . Let be a finite set of isometries of X which commute with the action of G on X and let be a real number equal to ±1.

Let d be the integer which is equal to 1 when X is a Hermitian symmetric space and equal to 0 otherwise. According to (2.27) and (2.28), we know that the multiplicity of the G-module is equal to d+1. Since its G-submodule is isomorphic to from Propositions 2.31 and 2.42 we deduce the following criteria for Guillemin rigidity and infinitesimal rigidity:

PROPOSITION 2.43. Let (X, g) be an irreducible symmetric space of compact type, which is not equal to a simple Lie group, and let be the element of which is the equivalence class of the irreducible G-module .

(i) If the inequality

holds for all , with = 1, and if the inequality

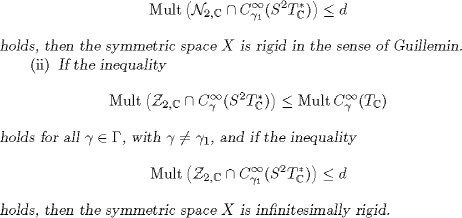
We choose a Cartan subalgebra of g and fix a system of positive roots of If W is a G-submodule of witthe dimension of its weight subspace, corresponding to the highest weight of is equal to the multiplicity of W. Thus according to Proposition 2.43,(i), to prove the Guillemin rigidity of X, it suffices to successively carry out the following steps:

According to Proposition 2.43,(ii), to prove the infinitesimal rigidity of X, it suffices to carry out the steps (i) and (ii) given above and then the following step:

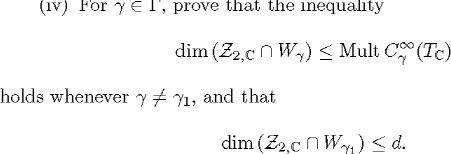
These methods for proving the rigidity of an irreducible symmetric space of compact type implement the criteria described at the end of 5. They were first used in [14] to show that the complex projective space is infinitesimally rigid (see 5, Chapter III).

8. Criteria for the rigidity of an irreducible symmetric space

We consider the symmetric space (X, g) of compact type of 4 and 7 and continue to view X as the homogeneous space G/K. We recall that a closed connected totally geodesic submanifold Y of X is a symmetric space; moreover, if x is a point of Y and the tangent space to Y at x is equal to the subspace V of Tx, then the submanifold Y is equal to the subset ExpxV of X (see 7 in Chapter IV of [36]).

Let be a family of closed connected totally geodesic submanifolds of X. We denote by the subspace of consisting of all symmetric 2-forms h which satisfy the following condition: for all subman-ifolds the restriction of h to Z is a Lie derivative of the metric of Z induced by g. By Lemma 1.1, we know that is a subspace of We consider the following properties which the family Fmight possess:

(I) If a section of Sover X satisfies the Guillemin condition, then its restriction to an arbitrary submanifold of X belonging to the family satisfies the Guillemin condition.

(II) Every submanifold of X belonging to Fis rigid in the sense of Guillemin.

(III) Every submanifold of X belonging to is infinitesimally rigid.

If the family possesses properties (I) and (II), then we see that

On the other hand, the restriction of an element of to an arbitrary sub-manifold of X belonging to the family satisfies the zero-energy condition; hence if the family possesses property (III), we have the inclusion

Z2 From Lemma 1.16, we obtain:

PROPOSITION 2.44. Let (X, g) be a symmetric space of compact type. Let F be a family of closed connected totally geodesic surfaces of X which is invariant under the group G, and let be a family of closed connected totally geodesic submanifolds of X. Assume that each surface of X belonging to F is contained in a submanifold of X belonging to F. A symmetric 2-form h on X belonging to satisfies the relation

PROPOSITION 2.45. Let (X, g) be a symmetric space of compact type. Let F be a G-invariant family of closed connected totally geodesic surfaces of X with positive constant curvature. Let h be an element of Then the following assertions are equivalent:

(i) The symmetric 2-form h belongs to

(iii) The symmetric 2-form h satisfies

PROOF: By Lemma 1.15, we know that assertion (i) implies (ii). Now suppose that assertion (ii) holds. Let Y be a totally geodesic submani-fold of X belonging to the family F and let be the natural imbedding. Then we have 0. If is the Riemannian metric on Y induced by g, by Proposition 1.14,(i) the restriction of h to the manifold Y satisfies Theorem 1.18 gives us the exactness of the sequence (1.51) corresponding to the Riemannian manifold (Y, gY ) with positive constant curvature; therefore the form on Y is a Lie derivative of the metric . Thus we know that h belongs to and so assertion (ii) implies (i). Since the equivalence of assertions (ii) and (iii) is a consequence of Proposition 1.14,(ii).

PROPOSITION 2.46. Let (X, g) be a symmetric space of compact type. Let Fbe a family of closed connected totally geodesic submanifolds of X.

(i) Suppose that each closed geodesic of X is contained in a subman-ifold of X belonging to the family Then we have the inclusion

(ii) Suppose that the sequence (1.24), corresponding to an arbitrary submanifold of X belonging to the family is exact. Let h be an element of C(S2T) satisfying the relation D1h = 0. Then h belongs to

(iii) Suppose that the hypothesis of (i) and of (ii) hold, and that the space X is infinitesimally rigid. Then the sequence (1.24) is exact.

PROOF: Let h be an element of C(S2T). First, suppose that h belongs to and that the hypothesis of (i) holds. Let be an arbitrary closed geodesic of X; then there is a submanifold Y of X belonging to the family containing . Let be the natural inclusion. Since the symmetric 2-form on Y is a Lie derivative of the metric of Y , the integral of h over vanishes; thus the symmetric 2-form h satisfies the zero-energy condition and assertion (i) holds. Next, let Y be an arbitrary submanifold of X belonging to the family and let be the natural inclusion. If D1,Y is the differential operator on the symmetric space Y defined in 1, Chapter I, according to formula (1.58) of Proposition 1.14 the relation D1h = 0 implies that and if the sequence (1.24) for Y is exact, it follows that is a Lie derivative of the metric of Y . Thus assertion (ii) is true. Finally, assertion (iii) is a direct consequence of (i) and (ii).

THEOREM 2.47. Let (X, g) be a symmetric space of compact type. Let F be a family of closed connected totally geodesic surfaces of X which is invariant under the group G, and let Fbe a family of closed connected totally geodesic submanifolds of X. Assume that each surface of X belonging to F is contained in a submanifold of X belonging to Suppose that the relation (1.48) and the equality

hold.

(i) A symmetric 2-form h on X belonging to is a Lie derivative of the metric g.

(ii) If the family possesses properties (I) and (II), then the symmetric space X is rigid in the sense of Guillemin.

(iii) If the family possesses property (III), then the symmetric space X is infinitesimally rigid.

PROOF: First, let h be a symmetric 2-form h on X belonging to By Proposition 2.44, we see that According to the equality (2.32), we therefore know that D1h = 0. By the relation (1.48) and Theorem 1.18, the sequence (1.24) is exact, and so we see that h is a Lie derivative of the metric g. Thus we have proved assertion (i). Now assume that the family satisfies the hypothesis of (i) (resp. of (ii)). Then we know that the space N2 (resp. the space is contained in Assertion (ii) (resp. (iii)) is a consequence of (i).

We now assume that (X, g) is an irreducible symmetric space of compact type; then we have Ric where is a positive real number.

THEOREM 2.48. Let (X, g) be an irreducible symmetric space of compact type. Let F be a family of closed connected totally geodesic surfaces of X which is invariant under the group G, and let be a family of closed connected totally geodesic submanifolds of X. Let E be a G-invariant sub-bundle 0T. Assume that each surface of X belonging to F is contained of in a submanifold of X belonging to and suppose that the relation

Assertion (i) is now a consequence of Proposition 2.37,(ii), with Next, let k be a symmetric 2-form on X belonging to According to the decomposition (1.11), we may write k as

where h is an element of satisfying div h = 0, which is uniquely determined by k, and where is a vector field on X. If k is invariant under a finite group of isometries of X, clearly h is also -invariant. Since is an element of the 2-form h also belongs to According to (i), we may write h = h1 + h2, where h1 is an element of E(X) and h2 is a section of E. If k satisfies the Guillemin (resp. the zero-energy) condition, according to Lemma 2.10 (resp. Lemma 2.6) so does h, and we may suppose that h1 also satisfies the Guillemin (resp. the zero-energy) condition. First, if then h1 and h are also sections of E; if moreover the equality (2.37) holds, then h vanishes and so k is equal to Next, under the hypotheses of (ii), if k is -invariant and satisfies the Guillemin (resp. the zero-energy) condition and if the equality (2.35) (resp. the equality (2.36)) holds, then h is a -invariant section of E; according to (2.34), we infer that h vanishes, and so k is equal to We have thus verified both assertions (ii) and (iii).

Since the differential operator corresponding to the family F of Theorem 2.48 is homogeneous, according to the proof of Proposition 2.37 the sections h1 and h2 given by Theorem 2.48,(i) satisfy the relations

The following theorem gives criteria for the Guillemin rigidity or the infinitesimal rigidity of an irreducible symmetric space of compact type.

Theorem 2.49. Let (X, g) be an irreducible symmetric space of compact type. Let F be a family of closed connected totally geodesic surfaces of X which is invariant under the group G, and let be a family of closed connected totally geodesic submanifolds of X. Let E be a G-invariant sub-bundle of Assume that each surface of X belonging to F is contained in a submanifold of X belonging to and suppose that the relations (2.33) and (2.37) hold.

(i) If the family possesses properties (I) and (II) and if the equality (2.35) holds, then the symmetric space X is rigid in the sense of Guillemin.

(ii) If the family possesses property (III) and if the equality (2.36) holds, then the symmetric space X is infinitesimally rigid.

PROOF: Under the hypotheses of (i) (resp. of (ii)), a symmetric 2-form h on X satisfying the Guillemin (resp. the zero-energy) condition belongs to by Theorem 2.48,(ii), with = {id}, we see that h is a Lie derivative of the metric g.

According to Proposition 2.13, we know that the equality (2.35) (resp. the equality (2.36)) is a necessary condition for the Guillemin rigidity (resp. the infinitesimal rigidity) of X.

If we take E = {0} in Theorem 2.49, we obtain the following corollary of Theorem 2.49:

THEOREM 2.50. Let (X, g) be an irreducible symmetric space of compact type. Let F be a family of closed connected totally geodesic surfaces of X which is invariant under the group G, and let be a family of closed connected totally geodesic submanifolds of X. Assume that each surface of X belonging to F is contained in a submanifold of X belonging to F. Suppose that the equality

holds. Then assertions (i) and (ii) of Theorem 2.49 hold.

Thus according to Theorem 2.50, when X is an irreducible space, in Theorem 2.47 in order to obtain assertion (ii) (resp. assertion (iii)) of the latter theorem we may replace the hypothesis that the relation (1.48) holds by the hypothesis that the equality (2.35) (resp. the equality (2.36)) holds.

We again assume that X is an arbitrary symmetric space of compact type. We consider the following properties which the family might possess:

(IV) If a one-form over X satisfies the Guillemin condition, then its restriction to an arbitrary submanifold of X belonging to the family satisfies the Guillemin condition.

(V) If Y is an arbitrary submanifold of X belonging to the family every form of degree one on Y satisfying the Guillemin is exact.

(VI) If Y is an arbitrary submanifold of X belonging to the family every form of degree one on Y satisfying the zero-energy is exact.

We consider the subset of 2Tconsisting of those elements of 2 which vanish when restricted 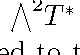to the submanifolds belonging to the family if the family is invariant under the group G, then is a sub-bundle of ²

THEOREM 2.51. Let (X, g) be a symmetric space of compact type. Let F and be two families of closed connected totally geodesic submanifolds of X. Assume that each submanifold of X belonging to F is contained in a submanifold of X belonging to , and suppose that

(i) If the family possesses properties (IV) and (V), then a differential form of degree one on X satisfies the Guillemin condition if and only if it is exact.

(ii) If the family possesses property (VI), then a differential form of degree one on X satisfies the zero-energy condition if and only if it is exact.

PROOF: Suppose that the family possesses properties (IV) and (V) (resp. possesses property (VI)). L be a 1-form on X satisfying the Guillemin (resp. the zero-energy) condition. Consider a submanifold Y of X belonging to the family According to our hypotheses, the restriction of to Y satisfies the Guillemin (resp. the zero-energy) condition; it follows that the 1-form on Y is closed. Hence the restriction of the 2-form to Y vanishes, and so the restriction of to an arbitrary submanifold of X belonging to the family F vanishes. From the relation (2.38), we infer that is closed. Since the cohomology group vanishes, the form is exact.