2.5 Small-World Network

Interestingly, in networks, the distance between a given node pair is known to be surprisingly small although the network size is very large. This property is referred to as the “small-world property” and was originally known as the “six degrees of separation” in sociology [18]. For example, the small-world property has been experimentally confirmed in the social network formed by the communication via internet tools such as instant-messaging systems [19].

2.5.1 Average Shortest Path Length

The distance between a node pair can be measured using the average shortest path length of a network, which is defined as

(2.14)

where d(i, j) indicates the shortest path length between nodes i and j. In addition, d(i, i) = 0 and d(i, j) =∞, if there is no shortest path between nodes i and j. Thus, the average shortest path length is only calculated in connected networks, in which there are shortest paths between all node pairs.

The ER random network model helps in explaining a small average shortest path length [7] when the probability p is not too small. When considering the breadth-first search from a node on the random network constructed with N nodes and probability p, the total number of nodes within a distance l is approximately expressed as

(2.15)

where k = p(N − 1) and is the average degree of random networks. Equating k ^l with N, we find that the average shortest path length is proportional to the logarithm of N:

(2.16)

In fact, the average shortest path length is almost similar to that of the random network model (see Table 2.2 and Refs. 2,7,18 for details).

Table 2.2 The Number of Nodes, Average Degree k, Average Path Length L, and Clustering Coefficient C of Representative Real-World Networks.

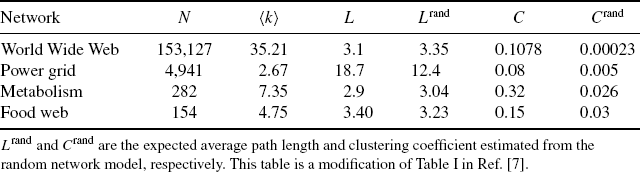
On the other hand, lattice networks have a large average shortest path length because they are embedded in dimensional spaces. For example, the one-dimensional lattice (Fig. 2.3a) and two-dimensional lattice (Fig. 2.3b) display L ∝ N and L ∝ N^1/2, respectively. It is clear that the lattice networks have no small-world property.

2.5.2 Ultrasmall-World Network

In addition, in the case of scale-free networks, there is a different relationship between the average shortest path length and network size. It is expected that the average shortest path length is smaller because of hubs (high-degree nodes). This relationship is characterized by the degree exponent γ. When γ > 3, L ∝ ln N as random networks. However, when 2 < γ < 3,

(2.17)

That is, scale-free networks are more small-world than random networks, indicating an ultrasmall-world property [20].

In addition, the average shortest path length L^nc of random networks with a given degree distribution (e.g., the configuration model) [21] is estimated as

(2.18)

where . . . indicates the average over nodes and γ_e ≈ 0.5772 is the Euler's constant. Of course, the above equation can be applied to the ER random network model and the BA model.