7.5 Proofs of the Main Theorems

We provide proofs for the symmetric bipartite case only. Note that the two other cases can be treated in a similar manner. However, nonbipartite graphs are much simpler to handle, because the calculations involve univariate instead of bivariate generating functions. On the other hand, the asymmetric bipartite case can be treated similar to the symmetric one, however, the calculations are even more technical due to the lack of symmetry and thus omitted.

Proof (of Theorem 7.1):We start considering the probability that no complex component occurs during the noncritical phase. The generating function of all such graphs is given by Equation (7.4). What is left, is to extract the coefficient of x^my^m and to divide this result by Equation (7.1), the corresponding total number of graphs. Recall that ε > 0 is fixed. We proceed considering the sequence of integer pairs (m, n) = (m, (1 − ε)m ). For technical reasons, we also define the ratio

which is always very close to ε. Thus, we may apply Lemma 7.4. It turns out that the saddle point is given by

Combining the result with Stirling's formula, we thus obtain

Finally, we can safely replace ε ' by without changing the expansion. All changes go into the error term .

Note that the critical case, that is Setup B, is somehow different. Lemma 7.4 can not be directly applied, because the saddle point would coincide with the singularity of the denominator. Thus, additional calculations and a different saddle point approach are required, see Ref. [7] for details.

Finally, we consider the probability that the complex part of a symmetric bipartite graph contains at most r more edges than nodes. To calculate an asymptotic expansion for a certain r, we thus proceed counting all graphs possessing excess exactly equal to s for all s less or equal than r. Such a graph contains 2m − n + s unrooted tree components, and a possibly empty set of unicyclic components:

An asymptotic expansion can again be derived by applying Lemma 7.4. In particular, we infer the same saddle point (x₀, y₀) as above. Finally, the probability that the excess equals at most r, is given by

We performed these calculations for r ≤ 2 using Maple and obtained in particular

Furthermore, a general proof of this property without the explicit calculation of an asymptotic approximation is based on the results of Ref. [8], together with the observations of Ref. [11].

Our further results concern the component structure of the graph. The proofs are again based on a generating function approach using Equation (7.4). Further, we introduce an additional variable to “mark” the parameter of interest, see for instance Refs. [16, 20–22] for further details of this method.

Again, recall that we fix ε > 0 and suppose that n = (1 − ε)m . We also note that it is sufficient to consider graphs of , the set of bipartite graphs without complex components, since all results for hold for unrestricted random bipartite graphs too. This can be easily seen in the following way. Consider a random variable ξ defined on the set G_m,m,n (with n = (1 − ε)m and ε > 0) and ξ ' its restriction to . Then the corresponding distribution functions by F_ξ and F_ξ' satisfy the relation

We proceed considering the cyclic components, since they are easier to handle.

Proof (of Theorem 7.3):In particular, we prove the following facts: The moment generating function of the number of cycles C_n,m and the number of cycles of length 2k C_n,m,k in a graph of (with n = (1 − ε)m and ε > 0) is given by

and

respectively, where s is any fixed real number. Since the moment-generating function of a Poisson distribution Po(λ) is given by we immediately deduce Theorem 7.3, once these formulas are proven.

We start with the calculation of the total number of cycles. For this purpose, we introduce a new variable that marks each cyclic component, that is, the exponent of counts the number of cycles. Equation (7.4) generalizes to

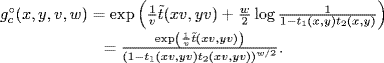
Of course, we have . Hence, the moment-generating function is given by

Again, the number of tree components equals 2m − n, thus the generating function simplifies to

We continue using Cauchy's formula and the double saddle point method described in Lemma 7.4. Note that we can use the same saddle point x₀ = y₀ = (1 − ε ')e^ε'−1. The calculation is even easier because it is sufficient to calculate the leading term.

We make use of the inequality

that is satisfied on the lines |x| = x₀, |y| = y₀ of integration. Furthermore, since , we obtain a corresponding result:

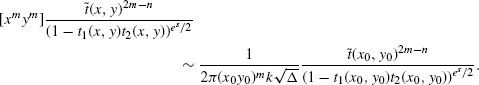
Thus, we obtain the moment-generating function

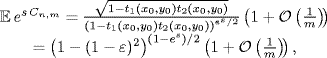
which completes the proof of the first part.

The proof of the second part is very similar, we just replace by the generating function

Hereby, is used to mark cycles of length 2k. Recall that the generating function of a component containing a cycle of length 2k is given by . We proceed as usual and yield

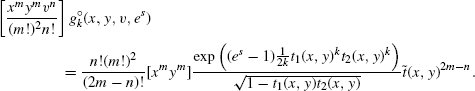
Finally, the moment-generating function of C_n,m,k equals

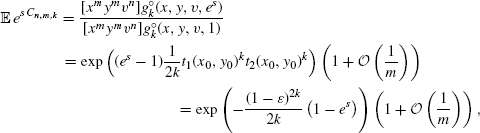
which completes the proof.

Next, we consider the number of vertices contained in cyclic components.

Proof (of Theorem 7.4): For the first part of the proof, we have to count the number of vertices V_n,m contained in cycles. We make use of the generating function

where the exponent of counts the number of cyclic points. Hence by again using the double saddle point methods, we get the claimed characteristic function, see Ref. [7] for details.

If we count the number of all vertices contained in cyclic components, the generating function modifies to

Here, we took care of all vertices of trees that are attached to cycles. It is straightforward to calculate asymptotic mean and variance.

Finally, we consider tree components.

Proof (of Theorem 7.2): The proof of this theorem is more complicated, since we also normalize depending on m. As in the formulation of Section 7.2, we use the following notation:

and

where k ≥ 1 is integer and 0 < ε < 1 holds.

First, we show that mean value and variance of the number of tree components T_m,n,k with k vertices of a randomly chosen graph of (with n = (1 − ε)m and ε > 0) are given by

(7.9)

and by

In what follows, we make use of the generating function of a bipartite tree components with 2k vertices. Because of Lemma 7.1, it is straightforward to calculate the number of unrooted trees possessing m₁ and m₂ nodes of each kind. Thus, it is easy to see that the generating function we are looking for is given by

We introduce the variable to mark trees which are of size k and obtain the following generating function

The lth factorial moment is then given by

The numerator of this expression simplifies to

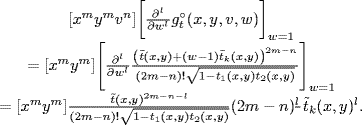
Now, we apply Lemma 7.4.4 to calculate an asymptotic expansion and obtain that the leading term of equals

Moreover, we conclude that the variance is of order O(m) too, thus its calculation requires to determine the next term of the asymptotic expansion. We do this in a semiautomatic way using Maple and obtain the proposed result.

To infer the limiting distribution, we make use of the characteristic function . It is given by

where we can use the simplification

Using a saddle point approach, it is possible to establish the following result, see Ref. [7] for details. For every k ≥ 1 and for every real number r we have, as m→ ∞,

where , what completes the proof.