8.5 Tree-Pattern Graph Kernels
Tree-based graph kernels [55] compare subtrees of graphs.
8.5.1 Definition
Let G = (V, E) be a graph and let T = (W, F), 
be a rooted directed tree. A tree pattern of G with respect to T consists of vertices 
such that
(8.14)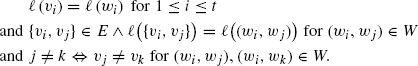 
Each vertex 
in the tree is assigned a vertex 
in the graph such that edges and labels match. The 
need not be distinct, as long as vertices assigned to sibling vertices in T are distinct (Fig. 8.3). The tree pattern counting functionψ(G, T) returns the number of times the tree pattern T occurs in the graph G, that is, the number of distinct tuples 
that are tree patterns of T in G.
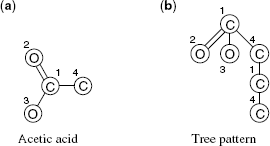
Figure 8.3 Tree patterns. Shown are the annotated graph of acetic acid (a) and a tree pattern contained in it (b). Numbers indicate assigned vertices. Note that vertices 1 and 4 appear twice; this is the equivalent of tottering in random walk kernels.
Let G = (V, E), G ' = (V ', E ') be graphs, let 
be a set of trees, and, let 
weight the trees in 
. Then
(8.15) 
is positive definite as it corresponds to a weighted inner product in the feature space indexed by the trees in 
. Specific examples of 
include weighting by size 
and by branching cardinality 
for balanced trees T of order h, where |T| denotes the number of vertices in T and branch(T) denotes branching cardinality. The parameter λ controls the weight put on complex tree patterns: more weight is put on them for λ > 1, and less for λ < 1. In the limit of λ → 0, only linear trees have nonzero weight, and the two kernels converge to the walk counting kernel. The branching cardinality weighting scheme can be extended to arbitrary trees of depth up to h.
8.5.2 Computation
Mahé and Vert [55] show how to compute such kernels using dynamic programming and the notion of neighborhood matching sets in time O(|V| |V '|h c2c), where c denotes the maximum vertex degree. Tottering (Fig. 8.3) can be prevented by additional constraints on ψ, where algorithms can be retained by transforming the input graphs, increasing runtime by a factor of
(8.16) 
8.5.3 Variants and Extensions
Shervashidze and Borgwardt [56] use the “naive vertex refinement” version of the Weisfeiler–Lehman graph isomorphism test [71] to define a fast graph kernel that compares subtrees of (labeled) graphs. The test iteratively constructs multisets of label strings 
that describe the neighborhood of each vertex; it terminates if either the multisets of the two graphs differ in any given round, or the maximum number h of iterations is reached. Consequently, the number of distinguishable isomorphic graphs depends on the free parameter h. The Weisfeiler–Lehman graph kernel simply counts the multiset strings common to both graphs:
(8.17)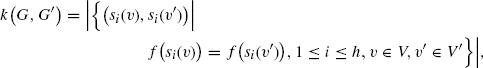 
where f is an injective function that compresses strings of concatenated labels. For two graphs, this kernel can be computed in time O(h |E|) using bucket sort [68] to exploit the bounded size of the label alphabet (and thus strings over it) in various sorting steps of the algorithm. The simultaneous computation of a kernel matrix for n graphs can be done in time O(n h max {|E1|, . . ., |En|} + n2h max {|V1|, . . ., |Vn|}) by using hashing to speed up label compression.