5
The Relative Power of Primitive Synchronization Operations
Imagine you are in charge of designing a new multiprocessor. What kinds of atomic instructions should you include? The literature includes a bewildering array of different choices: reading and writing to memory, getAndDecrement(), swap(), getAndComplement(), compareAndSet(), and many, many others. Supporting them all would be complicated and inefficient, but supporting the wrong ones could make it difficult or even impossible to solve important synchronization problems.
Our goal is to identify a set of primitive synchronization operations powerful enough to solve synchronization problems likely to arise in practice. (Of course, we might want to support other, nonessential synchronization operations for convenience.) To this end, we need some way to evaluate the power of various synchronization primitives: what synchronization problems they can solve, and how efficiently they can solve them.
A concurrent object implementation is wait-free if each method call finishes in a finite number of steps. A method is lock-free if it guarantees that infinitely often some method call finishes in a finite number of steps. We have already seen wait-free (and therefore by definition also lock-free) register implementations in Chapter 4. One way to evaluate the power of synchronization instructions is to see how well they support implementations of shared objects such as queues, stacks, trees, and so on. As we explained in Chapter 4, we evaluate solutions that are wait-free or lock-free, that is, guarantee progress without relying on outside support.1
We will see that all synchronization instructions are not created equal. If one thinks of primitive synchronization instructions as objects whose exported methods are the instructions themselves (in the literature these objects are often referred to as synchronization primitives ), one can show that there is an infinite hierarchy of synchronization primitives, such that no primitive at one level can be used for a wait-free or lock-free implementation of any primitives at higher levels. The basic idea is simple: each class in the hierarchy has an associated consensus number, which is the maximum number of threads for which objects of the class can solve an elementary synchronization problem called consensus. We will see that in a system of n or more concurrent threads, it is impossible to construct a wait-free or lock-free implementation of an object with consensus number n from an object with a lower consensus number.
5.1 Consensus Numbers
Consensus is an innocuous-looking, somewhat abstract problem that will have enormous consequences for everything from algorithm design to hardware architecture. A consensus object provides a single method decide(), as shown in Fig. 5.1. Each thread calls the decide() method with its input v at most once. The object’s decide () method will return a value meeting the following conditions:
![]()
Figure 5.1 Consensus object interface.
In other words, a concurrent consensus object is linearizable to a sequential consensus object in which the thread whose value was chosen completes its decide() first. Sometimes it is useful to focus on consensus problems where all inputs are either zero or one. We call this specialized problem binary consensus. To simplify the presentation, we focus here on binary consensus, but our claims apply verbatim to consensus in general.
We are interested in wait-free solutions to the consensus problem, that is, wait-free concurrent implementations of consensus objects. The reader will notice that since the decide() method of a given consensus object is executed only once by each thread, and there are a finite number of threads, by definition a lock-free implementation would also be wait-free and vice versa. Henceforth, we mention only wait-free implementations, and for historical reasons, call any class that implements consensus in a wait-free manner a consensus protocol.
We will restrict ourselves to object classes with deterministic sequential specifications (i.e., ones in which each sequential method call has a single outcome). 2
We want to understand whether a particular class of objects is powerful enough to solve the consensus problem. How can we make this notion more precise? If we think of such objects as supported by a lower level of the system, perhaps the operating system, or even the hardware, then we care about the properties of the class, not about the number of objects. (If the system can provide one object of this class, it can probably provide more.) Second, it is reasonable to suppose that any modern system can provide a generous amount of read–write memory for bookkeeping. These two observations suggest the following definition.
Definition 5.1.1
A class C solves n-thread consensus if there exist a consensus protocol using any number of objects of class C and any number of atomic registers.
Definition 5.1.2
The consensus number of a class C is the largest n for which that class solves n-thread consensus. If no largest n exists, we say the consensus number of the class is infinite.
Corollary 5.1.1
Suppose one can implement an object of class C from one or more objects of class D, together with some number of atomic registers. If class C solves n-consensus, then so does class D.
5.1.1 States and Valence
A good place to start is to think about the simplest interesting case: binary consensus (i.e., inputs 0 or 1) for 2 threads (call them A and B ). Each thread makes moves until it decides on a value. Here, a move is a method call to a shared object. A protocol state consists of the states of the threads and the shared objects. An initial state is a protocol state before any thread has moved, and a final state is a protocol state after all threads have finished. The decision value of any final state is the value decided by all threads in that state.
A wait-free protocol’s set of possible states forms a tree, where each node represents a possible protocol state, and each edge represents a possible move by some thread. Fig. 5.2 shows the tree for a 2-thread protocol in which each thread moves twice. An edge for A from node s to node s′ means that if A moves in protocol state s, then the new protocol state is s′. We refer to s′ as a successor state to s. Because the protocol is wait-free, the tree must be finite. Leaf nodes represent final protocol states, and are labeled with their decision values, either 0 or 1.
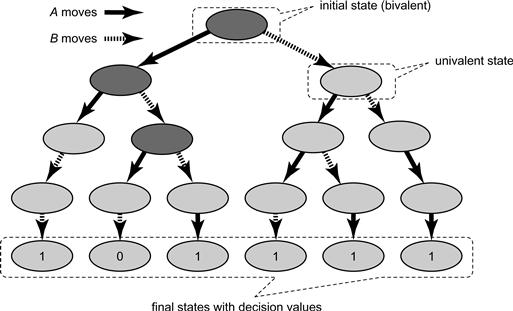
Figure 5.2 An execution tree for two threads A and B. The dark shaded nodes denote bivalent states, and the lighter ones univalent states.
A protocol state is bivalent if the decision value is not yet fixed: there is some execution starting from that state in which the threads decide 0, and one in which they decide 1. By contrast, the protocol state is univalent if the outcome is fixed: every execution starting from that state decides the same value. A protocol state is 1-valent if it is univalent, and the decision value will be 1, and similarly for 0-valent. As illustrated in Fig. 5.2, a bivalent state is a node whose descendants in the tree include both leaves labeled with 0 and leaves labeled with 1, while a univalent state is a node whose descendants include only leaves labeled with a single decision value.
Our next lemma says that an initial bivalent state exists. This observation means that the outcome of the protocol cannot be fixed in advance, but must depend on how reads and writes are interleaved.
Lemma 5.1.1
Every 2-thread consensus protocol has a bivalent initial state.
Proof
Consider the initial state where A has input 0 and B has input 1. If A finishes the protocol before B takes a step, then A must decide 0, because it must decide some thread’s input, and 0 is the only input it has seen (it cannot decide 1 because it has no way of distinguishing this state from the one in which B has input 0). Symmetrically, if B finishes the protocol before A takes a step, then B must decide 1, because it must decide some thread’s input, and 1 is the only input it has seen. It follows that the initial state where A has input 0 and B has input 1 is bivalent.
Lemma 5.1.2
Every n-thread consensus protocol has a bivalent initial state.
Proof
Left as an exercise.
A protocol state is critical if:
Lemma 5.1.3
Every wait-free consensus protocol has a critical state.
Proof
Suppose not. By Lemma 5.1.2, the protocol has a bivalent initial state. Start the protocol in this state. As long as there is some thread that can move without making the protocol state univalent, let that thread move. If the protocol runs forever, then it is not wait-free. Otherwise, the protocol eventually enters a state where no such move is possible, which must be a critical state.
Everything we have proved so far applies to any consensus protocol, no matter what class (or classes) of shared objects it uses. Now we turn our attention to specific classes of objects.
5.2 Atomic Registers
The obvious place to begin is to ask whether we can solve consensus using atomic registers. Surprisingly, perhaps, the answer is no. We will show that there is no binary consensus protocol for two threads. We leave it as an exercise to show that if two threads cannot reach consensus on two values, then n threads cannot reach consensus on k values, where n > 2 and k > 2.
Often, when we argue about whether or not there exists a protocol that solves a particular problem, we construct a scenario of the form: “if we had such a protocol, it would behave like this under these circumstances …”. One particularly useful scenario is to have one thread, say A, run completely by itself until it finishes the protocol. This particular scenario is common enough that we give it its own name: A runs solo.
Theorem 5.2.1
Atomic registers have consensus number 1.
Proof
Suppose there exists a binary consensus protocol for two threads A and B. We will reason about the properties of such a protocol and derive a contradiction.
By Lemma 5.1.3, we can run the protocol until it reaches a critical state s. Suppose A ’s next move carries the protocol to a 0-valent state, and B ’s next move carries the protocol to a 1-valent state. (If not, then switch thread names.) What methods could A and B be about to call? We now consider an exhaustive list of the possibilities: one of them reads from a register, they both write to separate registers, or they both write to the same register.
Suppose A is about to read a given register (B may be about to either read or write the same register or a different register), as depicted in Fig. 5.3. Consider two possible execution scenarios. In the first scenario, B moves first, driving the protocol to a 1-valent state s′, and then B runs solo and eventually decides 1. In the second execution scenario, A moves first, then B executes one operation, driving the protocol to a 0-valent state s. B then runs solo starting in s″ and eventually decides 0. The problem is that the states s′ and s″ are indistinguishable to B (the read A performed could only change its thread-local state which is not visible to B ), which means that B must decide the same value in both scenarios, a contradiction.
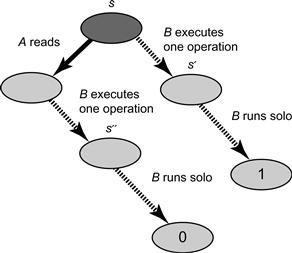
Figure 5.3 Case: A reads first. In the first execution scenario, B moves first, driving the protocol to a 1-valent state s′, and then B runs solo and eventually decides 1. In the second execution scenario, A moves first, driving the protocol to a 0-valent state s″. B then runs solo starting in s″ and eventually decides 0.
Suppose, instead of this scenario, both threads are about to write to different registers, as depicted in Fig. 5.4. A is about to write to r0 and B to r1. Let us consider two possible execution scenarios. In the first, A writes to r0 and then B writes to r1, so the resulting protocol state is 0-valent because A went first. In the second, B writes to r1 and then A writes to r0, so the resulting protocol state is 1-valent because B went first.
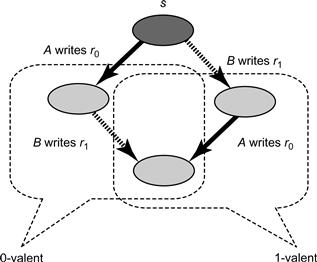
Figure 5.4 Case: A and B write to different registers.
The problem is that both scenarios lead to indistinguishable protocol states. Neither A nor B can tell which move was first. The resulting state is therefore both 0-valent and 1-valent, a contradiction.
Finally, suppose both threadswrite to the same register r, as depicted in Fig. 5.5. Again, consider two possible execution scenarios. In one scenario A writes first, the resulting protocol state s′ is 0-valent, B then runs solo and decides 0. In another scenario, B writes first, the resulting protocol state s″ is 1-valent, B then runs solo and decides 1. The problem is that B cannot tell the difference between s′ and s″ (because in both s′ and s″ it overwrote the register r and obliterated any trace of A’s write) so B must decide the same value starting fromeither state, a contradiction.

Figure 5.5 Case: A and B write to the same register.
Corollary 5.2.1
It is impossible to construct a wait-free implementation of any object with consensus number greater than 1 using atomic registers.
The aforementioned corollary is perhaps one of the most striking impossibility results in Computer Science. It explains why, if we want to implement lock-free concurrent data structures on modern multiprocessors, our hardware must provide primitive synchronization operations other than loads and stores (reads–writes).
5.3 Consensus Protocols
We now consider a variety of interesting object classes, asking how well each can solve the consensus problem. These protocols have a generic form, which we describe in Fig. 5.6. The object has an array of atomic registers in which each decide() method proposes its input value and then goes on to execute a sequence of steps in order to decide on one of the proposed values. We will devise different implementations of the decide() method using various synchronization objects.

Figure 5.6 The generic consensus protocol.
5.4 FIFO Queues
In Chapter 3, we saw a wait-free FIFO queue implementation using only atomic registers, subject to the limitation that only one thread could enqueue to the queue, and only one thread could dequeue from the queue. It is natural to ask whether one can provide a wait-free implementation of a FIFO queue that supports multiple enqueuers and dequeuers. For now, let us focus on a more specific problem: can we provide a wait-free implementation of a two-dequeuer FIFO queue using atomic registers?
Theorem 5.4.1
The two-dequeuer FIFO queue class has consensus number at least 2.
Proof
Fig. 5.7 shows a two-thread consensus protocol using a single FIFO queue. Here, the queue stores integers. The queue is initialized by enqueuing the value WIN followed by the value LOSE. As in all the consensus protocol considered here, decide() first calls propose(v), which stores v in proposed[], a shared array of proposed input values. It then proceeds to dequeue the next item from the queue. If that item is the value WIN, then the calling thread was first, and it decides on its own value. If that item is the value LOSE, then the other thread was first, so the calling thread returns the other thread’s input, as declared in the proposed[] array.

Figure 5.7 2-thread consensus using a FIFO queue.
The protocol is wait-free, since it contains no loops. If each thread returns its own input, then they must both have dequeued WIN, violating the FIFO queue specification. If each returns the other’s input, then they must both have dequeued LOSE, also violating the queue specification.
The validity condition follows from the observation that the thread that dequeued WIN stored its input in the proposed[] array before any value was dequeued.
Trivial variations of this program yield protocols for stacks, priority queues, lists, sets, or any object with methods that return different results if applied in different orders.
Corollary 5.4.1
It is impossible to construct a wait-free implementation of a queue, stack, priority queue, set, or list from a set of atomic registers.
Although FIFO queues solve two-thread consensus, they cannot solve 3-thread consensus.
Theorem 5.4.1
FIFO queues have consensus number 2.
Proof
By contradiction. Assume we have a consensus protocol for a thread A, B, and C. By Lemma 5.1.3, the protocol has a critical state s. Without loss of generality, we can assume that A’s next move takes the protocol to a 0-valent state, and B’s next move takes the protocol to a 1-valent state. The rest, as before, is a case analysis.
First, we know that A and B’s pending moves cannot commute, implying that they are both about to call methods of the same object. Second, we know that A and B cannot be about to read or write shared registers. It follows that they are about to call methods of a single queue object.
First, suppose A and B both call deq(), as depicted in Fig. 5.8. Let s′ be the protocol state if A dequeues and then B dequeues, and let s″ be the state if the dequeues occur in the opposite order. Since s′ is 0-valent, if C runs uninterrupted from s′, then it decides 0. Since s″ is 1-valent, if C runs uninterrupted from s″, then it decides 1. But s′ and s″ are indistinguishable to C (the same two items were removed from the queue), so C must decide the same value in both states, a contradiction.
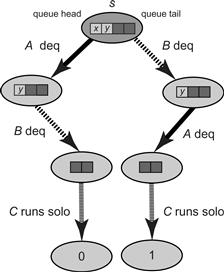
Figure 5.8 Case: A and B both call deq().
Second, suppose A calls enq(a) and B calls deq(). If the queue is nonempty, the contradiction is immediate because the two methods commute (each operates on a different end of the queue): C cannot observe the order in which they occurred. If the queue is empty, then the 1-valent state reached if B executes a dequeue on the empty queue and then A enqueues is indistinguishable to C from the 0-valent state reached if A alone enqueues. Notice that we do not really care what a deq() on an empty queue does, that is, aborts or waits, since this will not affect the state visible to C.
Finally, suppose A calls enq(a) and B calls enq(b), as depicted in Fig. 5.9. Let s′ be the state at the end of the following execution:
1. Let A and B enqueue items a and b in that order.
2. Run A until it dequeues a. (Since the only way to observe the queue’s state is via the deq() method, A cannot decide before it observes one of a or b.)
3. Before A takes any further steps, run B until it dequeues b.
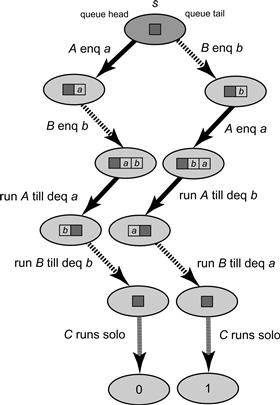
Figure 5.9 Case: A calls enq(a) and B calls enq(b). Notice that a new item is enqueued by A after A and B enqueued their respective items and before it dequeued (and B could have also enqueued items before dequeuing), but that this item is the same in both of the execution scenarios.
Let s″ be the state after the following alternative execution:
1. Let B and A enqueue items b and a in that order.
3. Before A takes any further steps, run B until it dequeues a.
Clearly, s′ is 0-valent and s″ is 1-valent. Both A ’s executions are identical until A dequeues a or b. Since A is halted before it can modify any other objects, B ’s executions are also identical until it dequeues a or b. By a now familiar argument, a contradiction arises because s′ and s″ are indistinguishable to C.
Trivial variations of this argument can be applied to show that many similar data types, such as sets, stacks, double-ended queues, and priority queues, all have consensus number exactly two.
5.5 Multiple Assignment Objects
In the (m, n-assignment) problem, for n ≥ m > 1 (sometimes called multiple assignment ), we are given an object with n fields (sometimes an n-element array). The assign() method takes as arguments m values ![]() , and m index values
, and m index values ![]() . It atomically assigns vj to array element ij. The read() method takes an index argument, i, and returns the ith array element. This problem is the dual of the atomic snapshot object (Chapter 4), where we assign to one field and read multiple fields atomically. Because snapshots can be implemented from read–write registers, Theorem 5.2.1 implies shapshot objects have consensus number 1.
. It atomically assigns vj to array element ij. The read() method takes an index argument, i, and returns the ith array element. This problem is the dual of the atomic snapshot object (Chapter 4), where we assign to one field and read multiple fields atomically. Because snapshots can be implemented from read–write registers, Theorem 5.2.1 implies shapshot objects have consensus number 1.
Fig. 5.10 shows a lock-based implementation of a (2,3)-assignment object. Here, threads can assign atomically to any two out of three array entries.

Figure 5.10 A lock-based implementation of a (2,3)-assignment object.
Theorem 5.5.1
There is no wait-free implementation of an (m,n)-assignment object by atomic registers for any n > m > 1.
Proof
It is enough to show that we can solve 2-consensus given two threads and a (2,3)-assignment object. (Exercise 75 asks one to justify this claim.) As usual, the decide() method must figure out which thread went first. All array entries are initialized with null values. Fig. 5.11 shows the protocol. Thread A writes (atomically) to fields 0 and 1, while thread B writes (atomically) to fields 1 and 2. Then they try to determine who went first. From A ’s point of view, there are three cases, as shown in Fig. 5.12:
![]() If A ’s assignment was ordered first, and B ’s assignment has not happened, then fields 0 and 1 have A ’s value, and field 2 is null. A decides its own input.
If A ’s assignment was ordered first, and B ’s assignment has not happened, then fields 0 and 1 have A ’s value, and field 2 is null. A decides its own input.
![]() If A ’s assignment was ordered first, and B ’s second, then field 0 has A ’s value, and fields 1 and 2 have B ’s. A decides its own input.
If A ’s assignment was ordered first, and B ’s second, then field 0 has A ’s value, and fields 1 and 2 have B ’s. A decides its own input.
![]() If B ’s assignment was ordered first, and A ’s second, then fields 0 and 1 have A ’s value, and 2 has B ’s. A decides B ’s input.
If B ’s assignment was ordered first, and A ’s second, then fields 0 and 1 have A ’s value, and 2 has B ’s. A decides B ’s input.

Figure 5.11 2-thread consensus using (2,3)-multiple assignment.
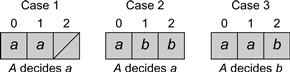
Figure 5.12 Consensus using multiple assignment: possible views.
A similar analysis holds for B.
Theorem 5.5.2
Atomic ![]() -register assignment for n > 1 has consensus number at least n.
-register assignment for n > 1 has consensus number at least n.
Proof
We design a consensus protocol for n threads ![]() . The protocol uses an
. The protocol uses an ![]() -assignment object. For convenience we name the object fields as follows. There are n fields
-assignment object. For convenience we name the object fields as follows. There are n fields ![]() where thread i writes to register ri, and
where thread i writes to register ri, and ![]() fields rij, where i > j, where threads i and j both write to field rij. All fields are initialized to null. Each thread i atomically assigns its input value to n fields: its single-writer field ri and its n−1 multi-writer registers rij. The protocol decides the first value to be assigned.
fields rij, where i > j, where threads i and j both write to field rij. All fields are initialized to null. Each thread i atomically assigns its input value to n fields: its single-writer field ri and its n−1 multi-writer registers rij. The protocol decides the first value to be assigned.
After assigning to its fields, a thread determines the relative ordering of the assignments for every two threads i and j as follows:
![]() Read rij. If the value is null, then neither assignment has occurred.
Read rij. If the value is null, then neither assignment has occurred.
![]() Otherwise, read ri and rj. If ri’s value is null, then j precedes i, and similarly for rj.
Otherwise, read ri and rj. If ri’s value is null, then j precedes i, and similarly for rj.
![]() If neither ri nor rj is null, reread rij. If its value is equal to the value read from ri, then j precedes i, else vice versa.
If neither ri nor rj is null, reread rij. If its value is equal to the value read from ri, then j precedes i, else vice versa.
Repeating this procedure, a thread can determine which value was written by the earliest assignment. Two example orderings appear in Fig. 5.13.
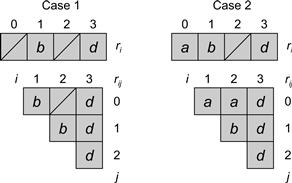
Figure 5.13 Two possible views of (4,10)-assignment solving consensus for 4 threads. In Part 1 only threads B and D show up. B is the first to assign and wins the consensus. In Part 2 there are three threads A, B, and D, and as before, B wins by assigning first and D assigns last. The order among the threads can be determined by looking at the pairwise order among any two. Because the assignments are atomic, these individual orders are always consistent and define the total order among the calls.
Note that multiple assignment solves consensus for any m > n > 1 threads while its dual structures and atomic snapshots, have consensus number at most one. Although these two problems may appear similar, we have just shown that writing atomically to multiple memory locations requires more computational power than reading atomically.
5.6 Read–Modify–Write Operations
Many, if not all, of the classical synchronization operations provided by multiprocessors in hardware can be expressed as read–modify–write (RMW) operations, or, as they are called in their object form, read–modify–write registers. Consider a RMW register that encapsulates integer values, and let ![]() be a set of functions from integers to integers. 3
be a set of functions from integers to integers. 3
A method is an RMW for the function set ![]() if it atomically replaces the current register value v with f (v), for some
if it atomically replaces the current register value v with f (v), for some ![]() , and returns the original value v. (Sometimes
, and returns the original value v. (Sometimes ![]() is a singleton set.) We (mostly) follow the Java convention that an RMW method that applies the function mumble is called getAndMumble().
is a singleton set.) We (mostly) follow the Java convention that an RMW method that applies the function mumble is called getAndMumble().
For example, the java.util.concurrent package provides an AtomicInteger class with a rich set of RMW methods.
![]() The getAndSet(v) method atomically replaces the register’s current value with v and returns the prior value. This method (also called swap()) is an RMW method for the set of constant functions of the type
The getAndSet(v) method atomically replaces the register’s current value with v and returns the prior value. This method (also called swap()) is an RMW method for the set of constant functions of the type ![]() .
.
![]() The getAndIncrement(v) method atomically adds 1 to the register’s current value and returns the prior value. This method (also called fetch-and-increment) is an RMW method for the function
The getAndIncrement(v) method atomically adds 1 to the register’s current value and returns the prior value. This method (also called fetch-and-increment) is an RMW method for the function ![]() .
.
![]() The getAndAdd(k) method atomically adds k to the register’s current value and returns the prior value. This method (also called fetch-and-add) is an RMW method for the set of functions
The getAndAdd(k) method atomically adds k to the register’s current value and returns the prior value. This method (also called fetch-and-add) is an RMW method for the set of functions ![]() .
.
![]() The compareAndSet() method takes two values, an expected value e, and an update value u. If the register value is equal to e, it is atomically replaced with u, and otherwise it is unchanged. Either way, the method returns a Boolean value indicating whether the value was changed. Informally,
The compareAndSet() method takes two values, an expected value e, and an update value u. If the register value is equal to e, it is atomically replaced with u, and otherwise it is unchanged. Either way, the method returns a Boolean value indicating whether the value was changed. Informally, ![]() if
if ![]() and u otherwise. Strictly speaking however, CompareAndSet() is not an RMW method for
and u otherwise. Strictly speaking however, CompareAndSet() is not an RMW method for ![]() , because an RMW method would return the register’s prior value instead of a Boolean value, but this distinction is a technicality.
, because an RMW method would return the register’s prior value instead of a Boolean value, but this distinction is a technicality.
![]() The get() method returns the register’s value. This method is an RMW method for the identity function f (v) = v.
The get() method returns the register’s value. This method is an RMW method for the identity function f (v) = v.
The RMW methods are interesting precisely because they are potential hardware primitives, engraved not in stone, but in silicon. Here, we define RMW registers and their methods in terms of synchronized Java methods, but, pragmatically, they correspond (exactly or nearly) to many real or proposed hardware synchronization primitives.
An RMW method is nontrivial if its set of functions includes at least one function that is not the identity function.
Theorem 5.6.1
Any nontrivial RMW register has consensus number at least 2.
Proof
Fig. 5.14 shows a 2-thread consensus protocol. Since there exists f in ![]() that is not the identity, there exists a value v such that
that is not the identity, there exists a value v such that ![]() . In the decide() method, as usual, the propose(v) method writes the thread’s input v to the proposed[] array. Then each thread applies the RMW method to a shared register. If a thread’s call returns v, it is linearized first, and it decides its own value. Otherwise, it is linearized second, and it decides the other thread’s proposed value.
. In the decide() method, as usual, the propose(v) method writes the thread’s input v to the proposed[] array. Then each thread applies the RMW method to a shared register. If a thread’s call returns v, it is linearized first, and it decides its own value. Otherwise, it is linearized second, and it decides the other thread’s proposed value.

Figure 5.14 2-thread consensus using RMW.
Corollary 5.6.1
It is impossible to construct a wait-free implementation of any nontrivial RMW method from atomic registers for two or more threads.
5.7 Common2 RMW Operations
We now identify a class of RMW registers, called Common2, that correspond to many of the common synchronization primitives provided by processors in the late Twentieth Century. Although Common2 registers, like all nontrivial RMW registers, are more powerful than atomic registers, we will show that they have consensus number exactly 2, implying that they have limited synchronization power. Fortunately, these synchronization primitives have by-and-large fallen from favor in contemporary processor architectures.
Definition 5.7.1
A set of functions ![]() belongs to Common2 if for all values v and all fi and fj in
belongs to Common2 if for all values v and all fi and fj in ![]() , either:
, either:
Definition 5.7.2
A RMW register belongs to Common2 if its set of functions ![]() belongs to Common2.
belongs to Common2.
For example, many RMW registers in the literature provide only one nontrivial function. For example, getAndSet() uses a constant function, which overwrites any prior value. The getAndIncrement() and getAndAdd() methods use functions that commute with one another.
Very informally, here is why RMW registers in Common2 cannot solve 3-thread consensus. The first thread (the winner) can always tell it was first, and each of the second and third threads (the losers) can each tell that they were losers. However, because the functions defining the state following operations in Common2 commute or overwrite, a loser thread cannot tell which of the others went first (was the winner), and because the protocol is wait-free, it cannot wait to find out. Let us make this argument more precise.
Theorem 5.7.1
Any RMW register in Common2 has consensus number (exactly) 2.
Proof
Theorem 5.6.1 states that any such register has consensus number at least 2. We need only to show that any Common2 register cannot solve consensus for three threads.
Assume by way of contradiction that a 3-thread protocol exists using only Common2 registers and read–write registers. Suppose threads A, B, and C reach consensus through Common2 registers. By Lemma 5.1.3, any such protocol has a critical state s in which the protocol is bivalent, but any method call by any thread will cause the protocol to enter a univalent state.
We now do a case analysis, examining each possible method call. The kind of reasoning used in the proof of Theorem 5.2.1 shows that the pending methods cannot be reads or writes, nor can the threads be about to call methods of different objects. It follows that the threads are about to call RMW methods of a single register r.
Suppose A is about to call a method for function fA, sending the protocol to a 0-valent state, and B is about to call a method for fB, sending the protocol to a 1-valent state. There are two possible cases:
1. As depicted in Fig. 5.15, one function overwrites the other: ![]() . Let s′ be the state that results if A applies fA and then B applies fB. Because s′ is 0-valent, C will decide 0 if it runs alone until it finishes the protocol. Let s″ be the state that results if B alone calls fB. Because s″ is 1-valent, C will decide 1 if it runs alone until it finishes the protocol. The problem is that the two possible register states
. Let s′ be the state that results if A applies fA and then B applies fB. Because s′ is 0-valent, C will decide 0 if it runs alone until it finishes the protocol. Let s″ be the state that results if B alone calls fB. Because s″ is 1-valent, C will decide 1 if it runs alone until it finishes the protocol. The problem is that the two possible register states ![]() and
and ![]() are the same, so s′ and s″ differ only in the internal states of A and B. If we now let thread C execute, since C completes the protocol without communicating with A or B, these two states look identical to C, so it cannot possibly decide different values from the two states.
are the same, so s′ and s″ differ only in the internal states of A and B. If we now let thread C execute, since C completes the protocol without communicating with A or B, these two states look identical to C, so it cannot possibly decide different values from the two states.
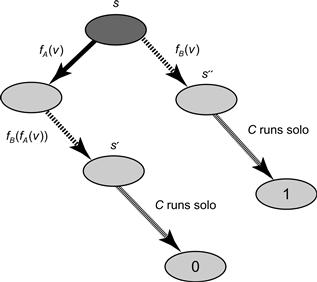
Figure 5.15 Case: two functions that overwrite.
2. The functions commute: ![]() . Let s′ be the state that results if A applies fA and then B applies fB. Because s′ is 0-valent, C will decide 0 if it runs alone until it finishes the protocol. Let s″ be the state that results if A and B perform their calls in the reverse order. Because s″ is 1-valent, C will decide 1 if it runs alone until it finishes the protocol. The problem is that the two possible register states
. Let s′ be the state that results if A applies fA and then B applies fB. Because s′ is 0-valent, C will decide 0 if it runs alone until it finishes the protocol. Let s″ be the state that results if A and B perform their calls in the reverse order. Because s″ is 1-valent, C will decide 1 if it runs alone until it finishes the protocol. The problem is that the two possible register states ![]() and
and ![]() are the same, so s′ and s″ differ only in the internal states of A and B. Now let thread C execute. Since C completes the protocol without communicating with A or B, these two states look identical to C, so it cannot possibly decide different values from the two states.
are the same, so s′ and s″ differ only in the internal states of A and B. Now let thread C execute. Since C completes the protocol without communicating with A or B, these two states look identical to C, so it cannot possibly decide different values from the two states.
5.8 The compareAndSet() Operation
We consider the compareAndSet() operation, a synchronization operation supported by several contemporary architectures. (For example, it is called CMPXCHG on the Intel Pentium™). This method is also known in the literature as compare-and-swap. A compareAndSet() takes two arguments: an expected value and an update value. If the current register value is equal to the expected value, then it is replaced by the update value; otherwise the value is left unchanged. The method call returns a Boolean indicating whether the value changed.
Theorem 5.8.1
A register providing compareAndSet() and get() methods has an infinite consensus number.
Proof
Fig. 5.16 shows a consensus protocol for n threads ![]() using the AtomicInteger class’s compareAndSet() method. The threads share an AtomicInteger object, initialized to a constant FIRST, distinct from any thread index. Each thread calls compareAndSet() with FIRST as the expected value, and its own index as the new value. If thread A ’s call returns true, then that method call was first in the linearization order, so A decides its own value. Otherwise, A reads the current AtomicInteger value, and takes that thread’s input from the proposed[] array.
using the AtomicInteger class’s compareAndSet() method. The threads share an AtomicInteger object, initialized to a constant FIRST, distinct from any thread index. Each thread calls compareAndSet() with FIRST as the expected value, and its own index as the new value. If thread A ’s call returns true, then that method call was first in the linearization order, so A decides its own value. Otherwise, A reads the current AtomicInteger value, and takes that thread’s input from the proposed[] array.

Figure 5.16 Consensus using compareAndSwap().
We note that having the compareAndSet() register in Theorem 5.8.1 provide a get() method is only a convenience, and so it follows that:
Corollary 5.8.1
A register providing only compareAndSet() has an infinite consensus number.
As we will see in Chapter 6, machines that provide primitive operations like compareAndSet()4 are asynchronous computation’s equivalents of the Turing Machines of sequential computation: any concurrent object that can be implemented, can be implemented in a wait-free manner on such machines. Thus, in the words of Maurice Sendak, compareAndSet() is the “king of all wild things.”
5.9 Chapter Notes
Michael Fischer, Nancy Lynch, and Michael Paterson [40] were the first to prove that consensus is impossible in a message-passing system where a single thread can halt. Their seminal paper introduced the “bivalency” style of impossibility argument widely used in the field of distributed computing. M. Loui and H. Abu-Amara [108] and Herlihy [62] were the first to extend this result to shared memory.
Clyde Kruskal, Larry Rudolph, and Marc Snir [133] coined the term read–modify–write operation as part of the NYU Ultracomputer project.
Maurice Herlihy [62] introduced the notion of a consensus number as a measure of computational power, and was the first to prove most of the impossibility and universality results presented in this chapter and Chapter 6.
The class Common2 that includes several common primitive synchronization operations was defined by Yehuda Afek and Eytan Weisberger and Hanan Weisman [5]. The “sticky-bit” object used in the exercises is due to Serge Plotkin [126].
The n-bounded compareAndSet() object with arbitrary consensus number n in Exercise 5.10 is based on a construction by Prasad Jayanti and Sam Toueg [81]. In the hierarchy used here, we say that X solves consensus if one can construct a wait-free consensus protocol from any number of instances of X and any amount of read–write memory. Prasad Jayanti [79] observed that one could also define resource-bounded hierarchies where one is restricted to using only a fixed number of instances of X, or a fixed amount of memory. The unbounded hierarchy used here seems to be the most natural one, since any other hierarchy is a coarsening of the unbounded one.
Jayanti also raised the question whether the hierarchy is robust, that is, whether an object X at level m can be “boosted” to a higher consensus level by combining it with another object Y at the same or lower level. Wai-Kau Lo and Vassos Hadzilacos [106] and Eric Schenk [144] showed that the consensus hierarchy is not robust: certain objects can be boosted. Informally, their constructions went like this: let X be an object with the following curious properties. X solves n-thread consensus but “refuses” to reveal the results unless the caller can prove he or she can solve an intermediate task weaker than n-thread consensus, but stronger than any task solvable by atomic read/write registers. If Y is an object that can be used to solve the intermediate task, Y can boost X by convincing X to reveal the outcome of an n-thread consensus. The objects used in these proofs are nondeterministic.
The Maurice Sendak quote is from Where the Wild Things Are [140].
Exercise 47. Prove Lemma 5.1.2.
Exercise 48. Prove that every n-thread consensus protocol has a bivalent initial state.
Exercise 49. Prove that in a critical state, one successor state must be 0-valent, and the other 1-valent.
Exercise 50. Show that if binary consensus using atomic registers is impossible for two threads, then it is also impossible for n threads, where n > 2. (Hint: argue by reduction: if we had a protocol to solve binary consensus for n threads, then we can transform it into a two-thread protocol.)
Exercise 51. Show that if binary consensus using atomic registers is impossible for n threads, then so is consensus over k values, where k > 2.
Exercise 52. Show that with sufficiently many n-thread binary consensus objects and atomic registers one can implement n-thread consensus over n values.
Exercise 53. The Stack class provides two methods: push(x) pushes a value onto the top of the stack, and pop() removes and returns the most recently pushed value. Prove that the Stack class has consensus number exactly two.
Exercise 54. Suppose we augment the FIFO Queue class with a peek() method that returns but does not remove the first element in the queue. Show that the augmented queue has infinite consensus number.
Exercise 55. Consider three threads, A, B, and C, each of which has a MRSW register, XA, XB, and XC, that it alone can write and the others can read.
In addition, each pair shares a RMWRegister register that provides only a compareAndSet() method: A and B share RAB, B and C share RBC, and A and C share RAC. Only the threads that share a register can call that register’s compareAndSet() method or read its value.
Your mission: either give a consensus protocol and explain why it works, or sketch an impossibility proof.
Exercise 56. Consider the situation described in Exercise 5.55, except that A, B, and C can apply a double compareAndSet() to both registers at once.
Exercise 57. In the consensus protocol shown in 5.7, what would happen if we announced the thread’s value after dequeuing from the queue?
Exercise 58. Objects of the StickyBit class have three possible states ⊥, 0, 1, initially ⊥. A call to write(v), where v is 0 or 1, has the following effects:
A call to read() returns the object’s current state.
1. Show that such an object can solve wait-free binary consensus (that is, all inputs are 0 or 1) for any number of threads.
2. Show that an array of ![]() StickyBit objects with atomic registers can solve wait-free consensus for any number of threads when there are m possible inputs. (Hint: you need to give each thread one single-writer, multi-reader atomic register.)
StickyBit objects with atomic registers can solve wait-free consensus for any number of threads when there are m possible inputs. (Hint: you need to give each thread one single-writer, multi-reader atomic register.)
Exercise 59. The SetAgree class, like the Consensus class, provides a decide() method whose call returns a value that was the input of some thread’s decide()call. However, unlike the Consensus class, the values returned by decide() calls are not required to agree. Instead, these calls may return no more than k distinct values. (When k is 1, SetAgree is the same as consensus.) What is the consensus number of the SetAgree class when k > 1?
Exercise 60. The two-thread approximate agreement class for a given ε is defined as follows. Given two threads A and B, each can call decide(xa) and decide(xb) methods, where xa and Xb are real numbers. These methods return values ya and yb respectively, such that ya and yb both lie in the closed interval ![]() , and
, and ![]() for ε > 0. Note that this object is nondeterministic.
for ε > 0. Note that this object is nondeterministic.
What is the consensus number of the approximate agreement object?
Exercise 61. Consider a distributed system where threads communicate by message-passing. A type A broadcast guarantees:
1. every nonfaulty thread eventually gets each message,
2. if P broadcasts M1 then M2, then every thread receives M1 before M2, but
3. messages broadcast by different threads may be received in different orders at different threads.
A type B broadcast guarantees:
1. every nonfaulty thread eventually gets each message,
2. if P broadcasts M1 and Q broadcasts M2, then every thread receives M1 and M2 in the same order.
For each kind of broadcast,
Exercise 62. Consider the following 2-thread QuasiConsensus problem:
Two threads, A and B, are each given a binary input. If both have input v, then both must decide v. If they have mixed inputs, then either they must agree, or B may decide 0 and A may decide 1 (but not vice versa).
Here are three possible exercises (only one of which works). (1) Give a 2-thread consensus protocol using QuasiConsensus showing it has consensus number 2, or (2) give a critical-state proof that this object’s consensus number is 1, or (3) give a read–write implementation of QuasiConsensus, thereby showing it has consensus number 1.
Exercise 63. Explain why the critical-state proof of the impossibility of consensus fails if the shared object is, in fact, a Consensus object.
Exercise 64. In this chapter we showed that there is a bivalent initial state for 2-thread consensus. Give a proof that there is a bivalent initial state for n thread consensus.
Exercise 65. A team consensus object provides the same decide() method as consensus. A team consensus object solves consensus as long as no more than two distinct values are ever proposed. (If more than two are proposed, the results are undefined.)
Show how to solve n-thread consensus, with up to n distinct input values, from a supply of team consensus objects.
Exercise 66. A trinary register holds values ⊥, 0, 1, and provides compareAndSet() and get() methods with the usual meaning. Each such register is initially ⊥. Give a protocol that uses one such register to solve n-thread consensus if the inputs of the threads are binary, that is, either 0 or 1.
Can you use multiple such registers (perhaps with atomic read–write registers) to solve n-thread consensus even if the threads' inputs are in the range ![]() , for K > 1. (You may assume an input fits in an atomic register.) Important: remember that a consensus protocol must be wait-free.
, for K > 1. (You may assume an input fits in an atomic register.) Important: remember that a consensus protocol must be wait-free.
Feel free to use all the atomic registers you want (they are cheap).
Exercise 67. Earlier we defined lock-freedom. Prove that there is no lock-free implementation of consensus using read–write registers for two or more threads.
Exercise 68.Fig. 5.17 shows a FIFO queue implemented with read, write, getAndSet() (that is, swap) and getAndIncrement() methods. You may assume this queue is linearizable, and wait-free as long as deq() is never applied to an empty queue. Consider the following sequence of statements.

Figure 5.17 Queue implementation.
![]() Both getAndSet() and getAndIncrement() methods have consensus number 2.
Both getAndSet() and getAndIncrement() methods have consensus number 2.
![]() We can add a peek() simply by taking a snapshot of the queue (using the methods studied earlier in the course) and returning the item at the head of the queue.
We can add a peek() simply by taking a snapshot of the queue (using the methods studied earlier in the course) and returning the item at the head of the queue.
![]() Using the protocol devised for Exercise 54, we can use the resulting queue to solve n-consensus for any n.
Using the protocol devised for Exercise 54, we can use the resulting queue to solve n-consensus for any n.
We have just constructed an n-thread consensus protocol using only objects with consensus number 2. Identify the faulty step in this chain of reasoning, and explain what went wrong.
Exercise 69. Recall that in our definition of compareAndSet() we noted that strictly speaking, compareAndSet() is not a RMW method for fe,u, because a RMW method would return the register’s prior value instead of a Boolean value. Use an object that supports compareAndSet() and get() to provide a new object with a linearizable NewCompareAndSet() method that returns the register’s current value instead of a Boolean.
Exercise 70. Define an n-bounded compareAndSet() object as follows. It provides a compareAndSet() method that takes two values, an expected value e, and an update value u. For the first n times compareAndSet() is called, it behaves like a conventional compareAndSet() register: if the register value is equal to e, it is atomically replaced with u, and otherwise it is unchanged, and returns a Boolean value indicating whether the change occurred. After compareAndSet() has been called n times, however, the object enters a faulty state, and all subsequent method calls return ⊥.
Show that an n-bounded compareAndSet() object has consensus number exactly n.
Exercise 71. Provide a wait-free implementation of a two-thread three-location Assign23 multiple assignment object from three compareAndSet() objects (that is, objects supporting the operations compareAndSet() and get() ).
Exercise 72. In the proof of Theorem 5.5.1, we claimed that it is enough to show that we can solve 2-consensus given two threads and an (2,3)-assignment object. Justify this claim.
Exercise 73. Prove Corollary 5.8.1.
Exercise 74. We can treat the scheduler as an adversary who uses the knowledge of our protocols and input values to frustrate our attempts at reaching consensus. One way to outwit an adversary is through randomization. Assume there are two threads that want to reach consensus, each can flip an unbiased coin, and the adversary cannot control future coin flips.
Assume the adversary scheduler can observe the result of each coin flip and each value read or written. It can stop a thread before or after a coin flip or a read or write to a shared register.
A randomized consensus protocol terminates with probability one against an adversary scheduler. Fig. 5.18 shows a plausible-looking randomized consensus protocol. Give an example showing that this protocol is incorrect.

Figure 5.18 Is this a randomized consensus protocol?
Exercise 75. One can implement a consensus object using read–write registers by implementing a deadlock- or starvation-free mutual exclusion lock. However, this implementation provides only dependent progress, and the operating system must make sure that threads do not get stuck in the critical section so that the computation as a whole progresses.
![]() Is the same true for obstruction-freedom, the nonblocking dependent progress condition? Show an obstruction-free implementation of a consensus object using only atomic registers.
Is the same true for obstruction-freedom, the nonblocking dependent progress condition? Show an obstruction-free implementation of a consensus object using only atomic registers.
![]() What is the role of the operating system in the obstruction-free solution to consensus? Explain where the critical-state-based proof of the impossibility of consensus breaks down if we repeatedly allow an oracle to halt threads so as to allow others to make progress.
What is the role of the operating system in the obstruction-free solution to consensus? Explain where the critical-state-based proof of the impossibility of consensus breaks down if we repeatedly allow an oracle to halt threads so as to allow others to make progress.
(Hint, think of how you could restrict the set of allowed executions.)
1 It makes no sense to evaluate solutions that only meet dependent progress conditions. This is because the real power of solutions based on dependent conditions such as obstruction-freedom or deadlock-freedom is masked by the contribution of the operating system they depend on.
2 We avoid nondeterministic objects since their structure is significantly more complex. See the discussion in the notes at the end of this chapter.
3 For brevity, we consider only registers that hold integer values, but they could equally well hold references to other objects.
4 Some architectures provide a pair of operations similar to get()/compareAndSet() called load-linked/store-conditional. In general, the load-linked method marks a location as loaded, and the store-conditional method fails if another thread modified that location since it was loaded. See Chapter 18 and Appendix B.
