6.1 Introduction

In Chapter 5, we considered a simple technique for proving statements of the form “there is no wait-free implementation of X by Y.” We considered object classes with deterministic sequential specifications.¹ We derived a hierarchy in which no object from one level can implement an object at a higher level (see Fig. 6.1). Recall that each object has an associated consensus number, which is the maximum number of threads for which the object can solve the consensus problem. In a system of n or more concurrent threads, it is impossible to construct a wait-free implementation of an object with consensus number n from an object with a lower consensus number. The same result holds for lock-free implementations, and henceforth unless we explicitly state otherwise, it will be implied that a result that holds for wait-free implementations holds for lock-free ones.

Figure 6.1. Concurrent computability and the universality hierarchy of synchronization operations.

Consensus Number	Object
1	atomic registers
2	getAndSet(), getAndAdd(), Queue, Stack
m	(m,m(m + 1)/2)-register assignment
∞	memory-to-memory move, compareAndSet(), Load-Linked/StoreConditional2

² See Appendix B for details.

The impossibility results of Chapter 5 do not by any means imply that wait-free synchronization is impossible or infeasible. In this chapter, we show that there exist classes of objects that are universal: given sufficiently many of them, one can construct a wait-free linearizable implementation of any concurrent object.

A class is universal in a system of n threads if, and only if it has a consensus number greater than or equal to n. In Fig. 6.1, each class at level n is universal for a system of n threads. A machine architecture or programming language is computationally powerful enough to support arbitrary wait-free synchronization if, and only if it provides objects of a universal class as primitives. For example, modern multiprocessor machines that provide a compareAndSet() operation are universal for any number of threads: they can implement any concurrent object in a wait-free manner.

This chapter describes how to use consensus objects to build a universal construction that implements any concurrent object. The chapter does not describe practical techniques for implementing wait-free objects. Like classical computability theory, understanding the universal construction and its implications will allow us to avoid the nae mistake of trying to solve unsolvable problems. Once we understand why consensus is powerful enough to implement any kind of object, we will be better prepared to undertake the engineering effort needed to make such constructions efficient.

6.2 Universality

A class C is universal if one can construct a wait-free implementation of any object from some number of objects of C and some number of read–write registers. Our construction uses multiple objects of class C because we are ultimately interested in understanding the synchronization power of machine instructions, and most machines allow their instructions to be applied to multiple memory locations. We allow an implementation to use multiple read–write registers because it is convenient for bookkeeping, and memory is usually in plentiful supply on modern architectures. To avoid distraction, we use an unlimited number of read–write registers and consensus objects, leaving the question of recycling memory as an exercise. We begin by presenting a lock-free implementation, later extending it to a slightly more complex wait-free one.

6.3 A Lock-Free Universal Construction

Fig. 6.2 shows a generic definition for a sequential object, based on the invocation–response formulation of Chapter 3. Each object is created in a fixed initial state. The apply() method takes as argument an invocation which describes the method being called and its arguments, and returns a response, containing the call’s termination condition (normal or exceptional) and the return value, if any. For example, a stack invocation might be push() with an argument, and the corresponding response would be normal and void.

Figure 6.2 A Generic sequential object: the apply() method applies the invocation and returns a response.

Figs. 6.3 and 6.4 show a universal construction that transforms any sequential object into a lock-free linearizable concurrent object. This construction assumes that sequential objects are deterministic: if we apply a method to an object in a particular state, then there is only one possible response, and one possible new object state. We can represent any object as a combination of a sequential object in its initial state and a log: a linked list of nodes representing the sequence of method calls applied to the object (and hence the object’s sequence of state transitions). A thread executes a method call by adding the new call to the head of the list. It then traverses the list, from tail to head, applying the method calls to a private copy of the object. The thread finally returns the result of applying its own operation. It is important to understand that only the head of the log is mutable: the initial state and nodes preceding the head never change.

Figure 6.3 The Node class.

Figure 6.4 The lock-free universal algorithm.

How do we make this log-based construction concurrent, that is, allow threads to make concurrent calls to apply()? A thread attempting to call apply() creates a node to hold its invocation. The threads then compete to append their respective nodes to the head of the log by running an n-thread consensus protocol to agree which node was appended to the log. The inputs to this consensus are references to the threads' nodes, and the result is the unique winning node.

The winner can then proceed to compute its response. It does so by creating a local copy of the sequential object and traversing the log, following next references from tail to head, applying the operations in the log to its copy, finally returning the response associated with its own invocation. This algorithm works even when apply() calls are concurrent, because the prefix of the log up to the thread’s own node never changes. The losing threads, which were not chosen by the consensus object, must try again to set the node currently at the head of the log (which changes between attempts) to point to them.

We now consider this construction in detail. The code for the lock-free universal construction appears in Fig. 6.4. A sample execution appears in Fig. 6.5. The object state is defined by a linked list of nodes, each one containing an invocation. The code for a node appears in Fig. 6.3. The node’s decideNext field is a consensus object used to decide which node is appended next in the list, and next is the field in which the outcome of that consensus, the reference to the next node, is recorded. The seq field is the node’s sequence number in the list. This field is zero while the node is not yet threaded onto the list, and positive otherwise. Sequence numbers for successive nodes in the list increase by one. Initially, the log consists of a unique sentinel node with sequence number 1.

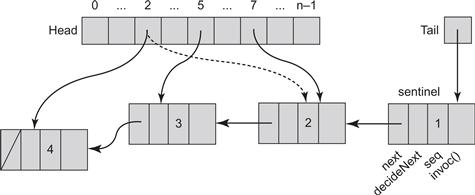
Figure 6.5 Execution of the lock-free universal construction. Thread 2 appends the second node in the log winning consensus on decideNext in the sentinel node. It then sets the node's sequence number from 0 to 2, and refers to it from its entry in the head[] array. Thread 7 loses the decideNext consensus at the sentinel node, sets the next reference and sequence number of the decided successor node to 2 (they were already set to the same values by thread 2), and refers to the node from its entry in the head[] array. Thread 5 appends the third node, updates its sequence number to 3 and updates its entry in the head[] array to this node. Finally, thread 2 appends the fourth node, sets its sequence number to 4, and refers to it from its entry in the head[] array. The maximal value in the head array keeps track of the head of the log.

The hard part about designing the concurrent lock-free universal construction is that consensus objects can be used only once. ³

In our lock-free algorithm in Fig. 6.4, each thread allocates a node holding its invocation, and repeatedly tries to append that node to the head of the log. Each node has a decideNext field, which is a consensus object. A thread tries to append its node by proposing as input to a consensus protocol on the head’s decideNext field. Because threads that do not participate in this consensus may need to traverse the list, the result of this consensus is stored in the node’s next field. Multiple threads may update this field simultaneously, but they all write the same value. When the thread’s node is appended, it sets the node’s sequence number.

Once a thread’s node is part of the log, it computes the response to its invocation by traversing the log from the tail to the newly added node. It applies each of the invocations to a private copy of the object, and returns the response from its own invocation. Notice that when a thread computes its response, all its predecessors' next references must already be set, because these nodes have already have been added to the head of the list. Any thread that added a node to the list has updated its next reference with the result of the decideNext consensus.

How do we locate the head of the log? We cannot track the head with a consensus object because the head must be updated repeatedly, and consensus objects can only be accessed once by each thread. Instead, we create a per-thread structure of the kind used in the Bakery algorithm of Chapter 2. We use an n-entry array head[], where head[i] is the last node in the list that thread i has observed. Initially all entries refer to the tail sentinel node. The head is the node with the maximum sequence number among the nodes referenced in the head[] array. The max() method in Fig. 6.3 performs a collect, reading the head[] entries and returning the node with the highest sequence number.

The construction is a linearizable implementation of the sequential object. Each apply() call can be linearized at the point of the consensus call adding the node to the log.

Why is this construction lock-free? The head of the log, the latest node appended, is added to the head[] array within a finite number of steps. The node’s predecessor must appear in the head array, so any node repeatedly attempting to add a new node will repeatedly run the max() function on the head array. It detects this predecessor, applies consensus on its decideNext field, and then updates the winning node’s fields, and including its sequence number. Finally, it stores the decided node in that thread’s head array entry. The new head node always eventually appears in head[]. It follows that the only way a thread can repeatedly fail to add its own node to the log is if other threads repeatedly succeed in appending their own nodes to the log. Thus, a node can starve only if other nodes are continually completing their invocations, implying that the construction is lock-free.

6.4 A Wait-Free Universal Construction

How do we make a lock-free algorithm wait-free? The full wait-free algorithm appears in Fig. 6.6. We must guarantee that every thread completes an apply() call within a finite number of steps, that is, no thread starves. To guarantee this property, threads making progress must help less fortunate threads to complete their calls. This helping pattern will show up later in a specialized form in other wait-free algorithms.

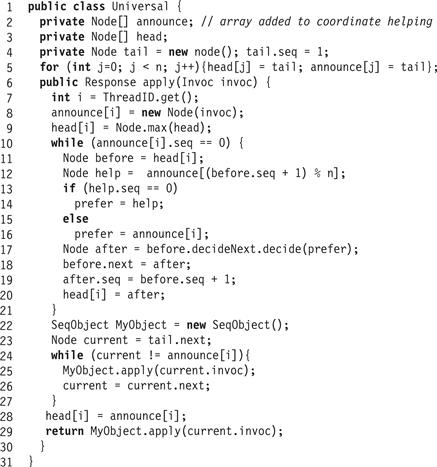
Figure 6.6 The wait-free universal algorithm.

To allow helping, each thread must share with other threads the apply() call that it is trying to complete. We add an n-element announce[] array, where announce[i] is the node thread i is currently trying to append to the list. Initially, all entries refer to the sentinel node, which has a sequence number 1. A thread i announces a node when it stores the node in announce[i].

To execute apply(), a thread first announces its new node. This step ensures that if the thread itself does not succeed in appending its node onto the list, some other thread will append that node on its behalf. It then proceeds as before, attempting to append the node into the log. To do so, it reads the head[] array only once (Line 9), and then enters the main loop of the algorithm, which it executes until its own node has been threaded onto the list (detected when its sequence number becomes non zero in Line 10). Here is a change from the lock-free algorithm. A thread first checks to see if there is a node that needs help ahead of it in the announce[] array (Line 12). The node to be helped must be determined dynamically because nodes are continually added to the log. A thread attempts to help nodes in the announce[] array in increasing order, determined by the sequence number modulo the width n of the announce[] array. We will prove that this approach guarantees that any node that does not make progress on its own will eventually be helped by others once its owner thread’s index matches the maximal sequence number modulo n. If this helping step were omitted, then an individual thread could be overtaken an arbitrary number of times. If the node selected for help does not require help (its sequence number is non zero in Line 13), then each thread attempts to append its own node (Line 16). (All announce[] array entries are initialized to the sentinel node which has a non zero sequence number.) The rest of the algorithm is almost the same as in the lock-free algorithm. A node is appended when its sequence number becomes non zero. In this case, the thread proceeds as before to compute its result based on the immutable segment of the log from the tail to its own node.

Fig. 6.7 shows an execution of the wait-free universal construction in which, starting from the initial state, thread 5 announces its new node and appends it to the log, and pauses before adding the node to head[]. Thread 7 then takes steps. The value of (before.seq + 1) mod n is 3, so thread 7 tries to help thread 2. Thread 7 loses the consensus on the sentinel node’s decideNext reference since thread 5 already won it, and thus completes the operations of thread 5, setting the node’s sequence number to 2 and adding thread 5’s node to the head[] array. Now imagine that thread 3 immediately announces its node. Then thread 7 succeeds in appending thread 3’s node, but again pauses immediately after setting thread 3’s node’s sequence number to 3, but before adding it to head[]. Now thread 3 wakes up. It will not enter the main loop because its node’s sequence number is non zero, but will continue to update head[] at Line 28 and compute its output value using a copy of the sequential object.

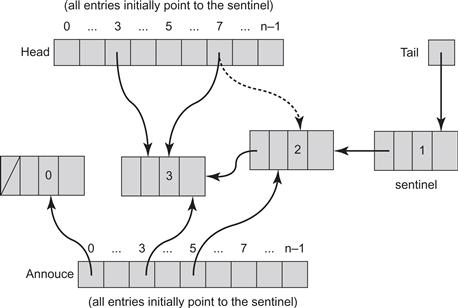
Figure 6.7 Execution of the wait-free universal construction. Thread 5 announces its new node and appends it to the log, but halts before adding the node to the head[] array. Another thread 7 will not see thread 5's node in the head[] array, and will attempt to help thread (before.seq + 1 mod n), which is equal to 3. When attempting to help thread 3, thread 7 loses the consensus on the sentinel node's decideNext reference since thread 5 already won. Thread 7 therefore completes updating the fields of thread 5's node, setting the node's sequence number to 2, and adding the node to the head[] array. Notice that thread 5's own entry in the head[] array is not yet set to its announced node. Next, thread 2 announces its node and thread 7 succeeds in appending thread 3's node, setting thread 3's node's sequence number to 3. Now thread 3 wakes up. It will not enter the main loop because its node's sequence number is non zero, but will continue to update the head[] array and compute its output value using a copy of the sequential object.

There is a delicate point to understand about these modifications to the lock-free algorithm. Since more than one thread can attempt to append a particular node to the log, we must make sure that no node is appended twice. One thread might append the node, and set the node’s sequence number, at the same time that another thread appended the same node and set its sequence number. The algorithm avoids this error because of the order in which threads read the maximum head[] array value and the sequence number of a node in the announce[] array. Let a be a node created by thread A and appended by threads A and B. It must be added at least once to head[] before the second append. Notice, however, that the before node read from head[A] by B (Line 11) must be a itself, or a successor of a in the log. Moreover, before any node is added to head[] (either in Line 20 or in Line 28), its sequence number is made non zero (Line 19). The order of operations ensures that B sets its head[B] entry (the entry based on which B ’s before variable will be set, resulting in an erroneous append) in Lines 9 or 20, and only then validates that the sequence number of a is non zero in Lines 10 or 13 (depending whether A or another thread performs the operation). It follows that the validation of the erroneous second append will fail because the sequence number of node a will already be non zero, and it will not be added to the log a second time.

Linearizability follows because no node is ever added twice, and the order in which nodes are appended to the log is clearly compatible with the natural partial order of the corresponding method calls.

To prove that the algorithm is wait-free, we need to show that the helping mechanism will guarantee that any node that is announced is eventually added to the head[] array (implying that it is in the log) and the announcing thread can complete computation of its outcome. To assist in the proof, it is convenient to define some notation. Let max(head[]) be the node with the largest sequence number in the head[] array, and let “c ∈ head[]” denote the assertion that node c has been assigned to head[i], for some i.

An auxiliary variable (sometimes called a ghost variable) is one that does not appear explicitly in the code, does not alter the program’s behavior in any way, yet helps us reason about the behavior of the algorithm. We use the following auxiliary variables:

The code reflecting the auxiliary variables and how they are updated appears in Fig. 6.8. For example, the statement

means that the node after is added to concur(j) for all threads j. The code statements within the angled brackets are considered to be executed atomically. This atomicity can be assumed because auxiliary variables do not affect the computation in any way. For brevity let us slightly abuse the notation by letting the function max() applied to a node or array of nodes return the maximal among their sequence numbers.

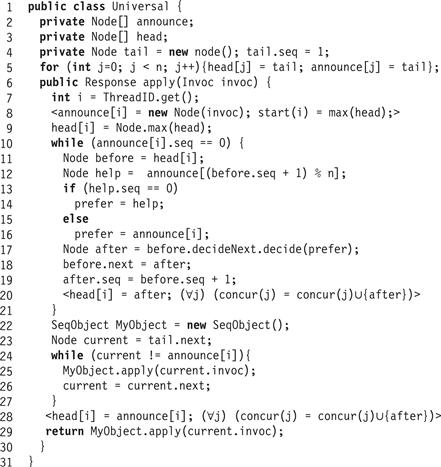
Figure 6.8 The wait-free universal algorithm with auxiliary variables. Operations in angled brackets are assumed to happen atomically.

Notice that the following property is invariant throughout the execution of the universal algorithm:

(6.4.1)

Lemma 6.4.1 places a bound on the number of nodes that can be appended while a method call is in progress. We now give a sequence of lemmas showing that when A finishes scanning the head[] array, either announce[A] is appended, or head[A] lies within n + 1 nodes of the end of the list.

6.5 Chapter Notes

The universal construction described here is adapted from Maurice Herlihy’s 1991 paper [62]. An alternative lock-free universal construction using load-linked–store-conditional appears in [60]. The complexity of this construction can be improved in several ways. Yehuda Afek, Dalia Dauber, and Dan Touitou [3] show how to improve the time complexity to depend on the number of concurrent threads, not the maximum possible number of threads. Mark Moir [118] shows how to design lock-free and wait-free constructions that do not require copying the entire object. James Anderson and Mark Moir [11] extend the construction to allow multiple objects to be updated. Prasad Jayanti [80] shows that any universal construction has worst-case Ω(n) complexity, where n is the maximal number of threads. Tushar Chandra, Prasad Jayanti, and King Tan [26] identify a large class of objects for which a more efficient universal construction exists.