2. Intuition Building with Center of Gravity Models
The simplest facility-location problem is the center of gravity (COG) problem. This is also a good place to start building intuition for more complicated models.
Center of gravity problems are ubiquitous in everyday life. When two children position themselves on a teeter-totter so that their different weights are in equilibrium, they are intuitively solving a two-body center of gravity problem. When a waitress loads a tray with an impressively large number of drinks and plates, and then balances the entire arrangement by positioning her hand in an unexpectedly off-center position, she is solving a center of gravity problem.
These problems come from our intuition of physics, and it is natural that the location of facilities in a supply chain borrows the terminology.
For logistics, a center of gravity problem is usually defined as selecting the location of a facility so that the weighted-average distance to all the demand points is minimized. So, in effect, the problem is similar to the waitress balancing the tray. The items on the tray are like the demand points, and the placement of her hand is like the facility location.
In the world of logistics, center of gravity problems are valued precisely because of their simplicity. A center of gravity solution suggests that facilities are located at the center (the “center of gravity”) of a collection of demand points (or in some instances, for firms with many suppliers, at the center of the supply points). Another way to think about this problem is to imagine a facility plopped down anywhere on the map. The demand points then engage in a tug of war to pull the facility closer. The larger demand points have more pull. If many small demand points are in a region, they will pull the facility closer to the region. The equilibrium point is when no demand point can pull the facility any closer without creating a solution that is worse for the entire system.
Center of gravity models are, by definition, clear-cut and not ambiguous. Problem formulations do not require a skilled professional to determine the cleanest approximation or modeling formula, but rather, merely require a correct and accurate specification. Thus, the same input data will inevitably yield the same result (or, in some cases, the same set of distinct, but functionally equivalent results). Center of gravity studies are useful both for building the intuition of the professional analyst and for validating the accuracy of his or her more comprehensive results.
Center of gravity studies are also powerful learning problems for someone new to the mathematical language of optimization. Because these problems are relatively simple, we can show how formal equations are designed to force a numerical engine to generate the optimal solution to the correct problem. In your career, you might be called upon to generate optimization formulas yourself. It is more likely that you will be required to use both off-the-shelf and customized software solutions that implement such formulations automatically. Regardless, it will be useful to have seen how a problem metamorphoses from a real-world “story problem” to a partially formulated collection of mathematical equations, and finally to a carefully tuned set of constraints, variables, and objective function.
By contrast, capturing the fiduciary nuances of a multimillion-dollar supply chain is a challenging process that calls upon the instinct and intuition of the professional modeler. Not every analyst will generate the exact same mathematical model for the same set of demand, supply, and pricing data. The plans and insights generated by a comprehensive strategic network design study will inevitably be a function of both the quality of the software tool and the skill of the analyst who yields it. Therefore, we find it very useful to start with the center of gravity models to help modelers and decision makers later tackle the complexity of modeling a full supply chain with its costs.
In the following two problems, we will cover the physics center of gravity and the practical center of gravity. In both cases, we will be locating a single site.
Problem 1: Physics Weighted-Average Centering
Consider a hypothetical country based on the principles of rational organization. Let’s call this country Logistica. The citizens of Logistica must choose a location for their capital.
Although all the citizens wish to live as near the seat of government as possible, it is impossible for all but a few of the citizens to relocate to their new capital. The map shown in Figure 2.1 shows the cities of Logistica, with the table showing the population. For more details on this problem, see the Excel file called Logistica.xls found on the book Web site.
Figure 2.1. Map of Logistica and Population by City
The planners of Logistica first decide to place the capital in the most central location possible. Initially, they choose their capital location by considering the boundaries of Logistica, and then selecting the location that centers the country geographically. This would be analogous to a waitress balancing a large, empty tray by placing her hand underneath the exact center.
However, the population of Logistica is not uniformly distributed across its interior. In general, there are more people in the East than the West, with a relatively empty middle. Thus, a geographically centered capital would incur pointlessly large travel times for everyone. The map in Figure 2.2 shows a square representing the approximate location of the geographic center. The planners calculate that this point is, on average, 471 miles from each citizen.
Figure 2.2. Approximate Geographic Center
Note: We can estimate the distance in miles between any two latitude and longitude points that are approximately halfway between the equator and the North or South Pole with the following equation:1
1 Designing and Managing the Supply Chain: Concepts, Strategies, and Case Studies. David Simchi-Levi, Philip Kaminsky, and Edith Simchi-Levi. McGraw-Hill/Irwin. 2008. Page 87.
Dist(miles)ab is the distance from point a to point b. Longa, Lata, Longb, and Latb are the longitudes and latitudes expressed as decimal numbers of point a and point b, respectively. If you want this measure to be in kilometers instead of miles, you simply change the 69 to 111.
Ever rational, the Logistica planners decide to borrow an idea from their colleagues in physics and instead locate the capital based on a weighted average of locations of the cities already scattered about the country. Thus, a single large metropolis in the East would be given more consideration than a smattering of hamlets in the West. A city with one million Logisticans would have more sway than a city with just 500,000 Logisticans. This is how a physicist would calculate a center of gravity point.
Formally, this sort of problem can be solved with a simple closed-form equation. In practice, this means that the problem can be solved with a relatively simple calculation engine, such as an Excel spreadsheet, or even with pencil and paper. Mathematically, this also means that a computer program is guaranteed to solve this problem quickly.
Specifically, the mathematical formula for physics center of gravity (or the weighted average location) would find the coordinates of Logistica’s capital as follows.
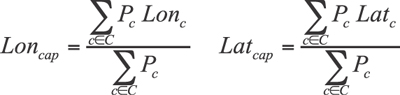
Here, Lon represents a city’s longitude, Lat represents its latitude, and P represents a city’s population. Here we are using the population as the weighting factor. In other problems, many different weighting factors can be used. In network problems, customer demand is the most common. These formulas compute the weighted average of the longitude and latitude of all the existing cities (represented by the set C). The physics center of gravity for Logistica using the previous Lon and Lat equations is shown in Figure 2.3
Figure 2.3. Logistica COG
With this approach, the weighted-average distance a citizen must travel is down to 388 miles. However, the location happens to fall in shark-infested waters offshore from a mountainous and deserted region. Obviously, the citizens of Logistica are not pleased with the resulting proposal. Though it’s good for a physics calculation, the planners quickly realize that the center of gravity calculation would not prove practical.
Logistica has its share of uninhabited coastlines, mountainous regions, treacherous canyons, and forest preserves. These would not be good locations for the capital. The planners realize that they need to exclude these locations as options.
After further digging into this simple formula, the planners (and three of the four authors of this book) were surprised to find that the formula was not minimizing what they thought it was! The formula does not minimize the weighted average distance to each city. Instead, the formula minimizes the demand multiplied by the distance squared. That is, a city that is 100 miles away is weighted by a factor of 10,000 but a city that is 110 miles away (10% further away) is weighted by a factor of 12,100 (21% more). The principles of physics would naturally square distance when finding the center of gravity. However, to the citizens of Logistica (and to real world supply chain practitioners), this definition does not necessarily make sense. In general, if you have to travel 10% further, it should be about a 10% increase in cost. Because this is counter-intuitive, see the sidebar for an additional explanation.
In summary and after more discussion, the planners of Logistica came up with a list of reasons for why the physics center of gravity calculations should not be used:
• It does not minimize what you want to minimize: weighted average distance.
• It might point to the middle of a large lake, an ocean, the top of a tall mountain, a wildlife preserve, or the middle of a barren desert.
• It will almost never land in a location that exploits existing infrastructure, such as a city, a population center with a workforce, railways, highways, or ports.
• The method cannot take advantage of true road distances or travel restrictions—it has to rely on straight-line estimates based on latitude and longitude.
• It cannot be extended to include factors like costs, capacities, different types of facilities, different products, multiple levels of facilities (hub and spoke, suppliers, warehouses, retailers, etc.), or other practical considerations.
What the Physics Center of Gravity Actually Minimizes
The idea of computing a weighted-average position from a set of cities, and of treating this weighted average as some sort of unattainable “ideal point,” has a deep-seated, intuitive appeal. There is a strong temptation to lend credence to the results of a clear mathematical equation. Indeed, when preparing and editing this book, the authors had to strongly resist describing the weighted-average technique as being some sort of hyperlogical, platonic ideal that is impaired only by a planner’s inability to conjure up a “Brasilia/Canberra” city from scratch. There is something jarring about the realization that the weighted-average computation does not, in fact, minimize the total person-miles of our hypothetical country. With this in mind, we have included a brief digression on this particular aspect of center of gravity modeling.
Consider a slightly idealized version of the American state of Oregon. The bulk of the population of Oregon lives along the Willamette Valley, a fertile crescent that meanders for roughly 100 miles, from Eugene, Oregon, in the middle of the state, to Portland, Oregon, along its northern border. Let’s simplify this situation slightly, and imagine that the entire population of Oregon lives in either Eugene or Portland, with a 4:9 ratio between the two populations and a total population of 1.3 million (we’ve made some assumptions to illustrate the point). Moreover, let’s assume that the Willamette Valley (and the associated highway) runs 100 miles due north, from Eugene to Portland. Our COG problem is now nicely simplified—we only need to determine how far south from Portland to place our capital.
We can thus let X represent the distance from Portland to our capital. If X = 0 then Portland will be selected as our capital. If X = 100 then Eugene is the capital, and if X = 50 then the capital will be placed halfway in between the two cities.
Given our assumption that 400,000 people live in Eugene, and the remaining 900,000 live in Portland, the formula for computing total person-miles of travel will be as follows:
T = (9000000)X + (400000)(100–X)
Suppose we want to find the X that yields the smallest result for T, with the caveat that X must be between 0 and 100, inclusive. This result is easy to obtain from simple trial and error. If we let X = 0, then we obtain the result T = 40,000,000 (40 million). If we let X = 100, then we obtain the result T = 90,000,000 (90 million). If we let X = 50, then we obtain the result T = 65,000,000 (65 million).
In other words, if we place the capital in Portland, then, on average, an Oregonian will need to travel 31 miles to visit the capital (40 million person-miles divided by 1.3 million population). There is something jarring about the realization that the weighted average computation (the physics center of gravity calculation) does not, in fact, minimize the total person-mile (or with division by the total population, the weighted average distance a citizen must travel) of our hypothetical country. If we place the capital halfway between the two cities, we get a “split the difference” average trip of 50 miles.
Although these examples do not constitute a proof, it should be easy to see that we can minimize total person-miles simply by placing the capital in the larger city of Portland. Every location that is further away from Portland increases the total commuting distance for the citizens of Portland more than is offset by the total decrease in distance for the citizens of Eugene. This is true precisely because there are more Portlanders than Eugeneans.
However, consider the “physics weighted average” positioning of the capital. In our version of Oregon, we can simplify the map to a straight line (the same principles will apply on a globe using latitude and longitude).
With Portland at the 0 mile marker and Eugene at the 100 mile marker, the X variable again represents location of our capital. If we locate our capital using the physics weighted-average calculation, this value will be
X = ((900000)(0) + (400000)(100))/1300000≈31
That is to say, a weighted-average position locates our capital about 31 miles south of Portland. The total person-miles for this location will be 55 million, or 43 miles per person.
This is clearly worse than the result obtained by placing the capital at Portland, because we are now requiring Oregonians to travel an average of 43 miles to the capital versus the 31 from before.
This shows that weighted average location computation (the physics center of gravity) does not minimize the average distance. It is minimizing something else!
The weighted average location computation is actually minimizing the demand times the distance squared. To show this, we will need a little calculus. Let S be the same as T except we are squaring the distance now. The formula becomes
S = (900000)X2 + (400000)(100–X)2
Now, as before, we might ask what value for X results in the smallest value for S. In this case, there are some relatively straightforward ideas from calculus that can be applied. Without getting bogged down in the mathematics, the minimization of S can be found by considering S to be a function of X, taking the derivative of S relative to X, setting this derivative to zero, and solving for X. This appears as follows:
S’ = 2(900000)X – 2(400000)(100–X) = 0 →
(2(900000) + 2(400000))X = 2(400000)(100) →
X = 2(400000)(100)/(2(900000) + 2(400000)) ≈ 31
Thus, when we place our capital at the weighted-average location that lies 31 miles south of Portland, we minimize not the total citizen miles (i.e., the T value) but rather the total citizen miles-squared (i.e., the S value).
For graphical evidence, see Figure 2.4. The x-axis represents the distance of the capital from Portland. So, 0 is at Portland, 10 would be 10 miles away from Portland, and 100 would be in Eugene. The Y-Axis on the left and the line with the square markers shows the demand weighted average distance. You can see that this steadily increases as we move the capital further from Portland. The Y-Axis on the right and the line with the diamond markers shows the total demand times distance squared (in millions). This is the physics center of gravity and you can see that its minimum point is about 31 miles from Portland.
Figure 2.4. Graph with Different Center of Gravity Objectives
This sidebar has shown that the weighted-average position, while being most true to the “center of gravity” concept that is used by physicists, will minimize a value that does not have meaning for supply chain planners. Despite its intuitive appeal, it will give us an answer that is different from what we are actually trying to achieve. The physics center of gravity is good for balancing a tray or ensuring that flying airplanes are stable, but not very good for supply chain network design.
Problem 2: Practical Center of Gravity
The planners of Logistica, having learned that applying the physics center of gravity is flawed for network design problems, now try to find an approach to minimize the average distance traveled.
Some planners start to ask the question of what happens when they simply pick the three Eastern cities of 5, 16, and 11 (see Figure 2.5).
Figure 2.5. Picking Cities 5, 16, and 11
For each of these locations, a clever planner quickly calculates some additional key statistics to better understand these choices for a capital city. Figure 2.6 shows the weighted-average distance (miles) and the percentage of the population within 100, 200, and 300 miles of the city selected (shown in the column header).
Figure 2.6. Key Statistics for 5, 16, and 11
The planners of Logistica started to feel like they were on to a good approach. Maybe there is a lot more to this simple problem than they realized. First, they confirmed that the physics center of gravity solution (COG in the table) did not do very well on the key statistics for judging potential locations. It had a higher average distance and had very few citizens with 100, 200, or 300 miles radius. Because the objective of the physics center of gravity does not minimize average distance or percentage of customers close to the capital, this result is not surprising. The planners also realize that there may be trade-offs they have to make. For example, it may be important that a large portion of the population can easily get to the capital city, even if the average distance is a bit longer.
Of course, the curious planners want to know whether even better solutions existed. Because they are picking only one city as the capital, they can easily calculate the key statistics for all 25 cities. The full set of statistics can be seen in the spreadsheet, Logistica.xls. Figure 2.7 shows the statistics for a few key cities.
Figure 2.7. Key Statistics for Other Key Cities
City 22 is at the extreme western point and, not surprisingly, does poorly on all the key statistics. Its citizens have grown used to the long travel distances to visit other Logistica cities and would not be surprised by this. Working our way east to the middle of the country, from City 22, we also analyze Cities 20 and 15. Neither does very well on the statistics, although 15 (which is close to the landmass center of the country) has a relatively decent weighted-average distance.
Cities 4 and 10 are much more interesting. Geographically, these cities are getting farther and farther away from any physics or mathematical center. However, they start to dominate on the percentage of the population that is within a certain distance. Both of these cities have 24% of the population within 100 miles—much higher than City 11’s 17%. Likewise, City 10 dominates on the percentage within 200 and 300 miles. City 10 happens to be very close to the vast majority of the citizens of Logistica.
The planners quickly realize that comparing candidate locations allows them to exploit the richness of the problem (trading off average distance with percentage within a certain distance).
We now start to formulate a more realistic problem. We will formalize this in Chapter 3, “Locating Facilities Using a Distance-Based Approach.” This problem selects the most central location from a list of possible candidates. Typically, the list of candidates is the entire list of cities. However, this is not a hard requirement, and a center of gravity problem could be forced to select from a subset of the cities, or could be allowed to select from among proposed locations that currently have no population at all.
You might think that by restricting the selection problem to a limited set of candidates, the problem would become easier to solve. In the case of just picking one city, this is true if you have the time to enumerate all the solutions like the planners of Logistica did. However, as you expand the problem, nothing could be further from the truth.
This more realistic and practical formulation of the problem is best solved with linear and integer programming techniques. This technique, which we will explore further in the next chapter, allows us to minimize the weighted-average distance (or other factors), picks locations we can actually use, and is very easily expanded to include other factors as well.
Lessons Learned from Center of Gravity Problems
In this chapter, we learned that locating a single point relative to demand is best done by minimizing the average weighted distance. You can accomplish this by picking your solution from a candidate list of locations. When picking one point, it is often simple enough to list out all the combinations and pick the best one. In the end, when you have a solution, it will tend to pull the single point close to as much demand as possible.
Although the physics concept of a weighted-average central point is appealing to our intuition and mathematically easy, it is flawed for network design studies. It can lead to undesirable locations as it is really minimizing the population multiplied by miles squared. Also, it cannot be extended to take advantage of existing infrastructure, road distance, or other facility costs.
End-of-Chapter Questions
1. Given the analysis presented in this chapter, where would you put the capital of Logistica and why? What factors went into your decision?
2. Besides the weighted-average distance and the percentage of customers within a certain distance of the capital, what other factors might the citizens of Logistica want to consider? Of these factors, which are quantifiable and which are qualitative?
3. If the planners of Logistica had been lucky enough for their first calculation to have picked an existing city, why should they still analyze other cities?
4. Name a reason why minimizing weighted-average distance is more important than maximizing the percentage of customers within a certain distance. Now, name a reason why maximizing the percentage of customers within a certain distance is more important than why minimizing weighted-average distance.
5. If instead of weighting the problem by the population of each city, assume that the analysis was done with each city having equal weight. That is, what matters is how close a city is to the capital, not how many people live there.
a. Which capital location is now the best from an average-distance point of view?
b. Which capital is now the best in terms of the number of cities within 100, 200, and 300 miles?
c. Does this make the analysis easier or harder? Why?
6. What if the western part of Logistica decided it needed a capital city as well? Assume that City 15 was the easternmost city in this region. What is the best location for the capital of the western half of Logistica? Why?
7. Often, when logistics practitioners think about having some automatic way of picking a latitude and longitude, they think about a problem where the four cities form a square on a map. In this case, let’s assume that each city has a population of one million and the latitude and longitude of the four points are (15,155), (15,158), (18,155), and (18,158).
a. What is the latitude and longitude of the physics center of gravity?
b. What is the average distance to each of the cities from this point?
c. Is there a better point that would minimize the weighted-average distance?
d. If the population of City 1 were five million, what would be the physics center of gravity latitude and longitude?
e. Sticking with the assumption in part (d), is there a location with a lower weighted-average distance? If so, where is the point?
f. Provide some reasons why the example in parts (a) to (c) (that is, four points, forming a square, each with equal demand) is not likely to occur in real-world supply chain network design problems?
8. In both the physics and the practical center of gravity, we used the straight-line distance from a city to the capital. Why could we use actual road distance in the practical center of gravity but not in the physics center of gravity?