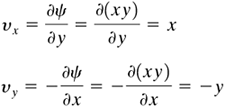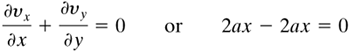3.9. OTHER METHODS FOR SOLUTION OF DIFFERENTIAL EQUATIONS OF MOTION

3.9A. Introduction

In Section 3.8 we considered examples where the Navier-Stokes differential equations of motion could be solved analytically. These cases were used where there was only one non-vanishing component of the velocity. To solve these equations for flows in two and three directions is quite complex.

In this section we will consider some approximations that simplify the differential equations to allow us to obtain analytical solutions. Terms will be omitted which are quite small compared to the terms retained.

Three cases will be considered in this section: inviscid flow, potential flow, and creeping flow. The fourth case, for boundary-layer flow, will be considered in Section 3.10. The solution of these equations may be simplified by using a stream function ψ(x, y) and/or a velocity potential φ(x, y) rather than the terms of the velocity components ν_x, ν_y, and v_z.

3.9B. Stream Function

The stream function ψ(x, y) is a convenient parameter by which we can represent two-dimensional, steady, incompressible flow. This stream function ψ in m²/s is related to the velocity components ν_x and ν_y by

Equation 3.9-1

These definitions of ν_x and ν_y can then be used in the x and y components of the differential equation of motion, Eqs. (3.7-36) and (3.7-37), together with ν_z = 0, to obtain a differential equation for ψ that is equivalent to the Navier-Stokes equation. Details are given elsewhere (B2).

The stream function is very useful because of its physical significance, that is, that in steady flow, lines defined by ψ = constant are streamlines, which are the actual curves traced out by the particles of fluid. A stream function exists for all two-dimensional, steady, incompressible flow whether viscous or inviscid and whether rotational or irrotational.

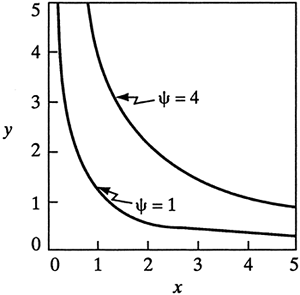
EXAMPLE 3.9-1. Stream Function and Streamlines The stream function relationship is given as ψ = xy. Find the equations for the components of velocity. Also plot the streamlines for a constant ψ = 4 and ψ = 1. Solution: Using Eq. (3.9-1), To determine the streamline for ψ = constant = 1 = xy, assume that y = 0.5 and solve for x: Hence, x = 2. Repeating, for y = 1, x = 1; for y = 2, x = 0.5; for y = 5, x = 0.2, and so on. Doing the same for ψ = constant = 4, the streamlines for ψ = 1 and ψ = 4 are plotted in Fig. 3.9-1. A possible flow model is flow around a corner. Figure 3.9-1. Plot of streamlines for ψ = xy for Example 3.9-1.

3.9C. Differential Equations of Motion for Ideal Fluids (Inviscid Flow)

Special equations for ideal or inviscid fluids can be obtained for a fluid having a constant density and zero viscosity. These are called the Euler equations. Equations (3.7-36)-(3.7-38) for the x, y, and z components of momentum become

Equation 3.9-2

Equation 3.9-3

Equation 3.9-4

At very high Reynolds numbers the viscous forces are quite small compared to the inertia forces and the viscosity can be assumed as zero. These equations are useful in calculating pressure distribution at the outer edge of the thin boundary layer in flow past immersed bodies. Away from the surface outside the boundary layer this assumption of an ideal fluid is often valid.

3.9D. Potential Flow and Velocity Potential

The velocity potential or potential function ϕ(x, y) in m²/s is useful in inviscid flow problems and is defined as

Equation 3.9-5

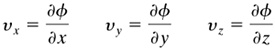
This potential exists only for a flow with zero angular velocity, or irrotationality. This type of flow of an ideal or inviscid fluid (ρ = constant, μ = 0) is called potential flow. Additionally, the velocity potential ϕ exists for three-dimensional flows, whereas the stream function does not. The vorticity of a fluid is defined as follows:

Equation 3.9-6

or,

Equation 3.9-7

where 2ω_z is the vorticity and ω_z in s^-1 is angular velocity about the z axis. If 2ω_z = 0, the flow is irrotational and a potential function exists.

Using Eq. (3.6-24), the conservation-of-mass equation for flows in the x and y directions is as follows for constant density:

Equation 3.9-8

Differentiating ν_x in Eq. (3.9-5) with respect to x and ν_y with respect to y and substituting into Eq. (3.9-8),

Equation 3.9-9

This is Laplace's equation in rectangular coordinates. If suitable boundary conditions exist or are known, Eq. (3.9-9) can be solved to give ϕ(x, y). Then the velocity at any point can be obtained using Eq. (3.9-5). Techniques for solving this equation include using numerical analysis, conformal mapping, and functions of a complex variable, and are given elsewhere (B2, S3). Euler's equations can then be used to find the pressure distribution.

When the flow is inviscid and irrotational, a similar type of Laplace equation is obtained from Eq. (3.9-7) for the stream function:

Equation 3.9-10

Lines of constant φ are called equal potential lines and for potential flow are everywhere perpendicular (orthogonal) to lines of constant ψ. This can be proved as follows. A line of constant ψ would be such that the change in ψ is zero:

Equation 3.9-11

Then, substituting Eq. (3.9-1) into the above,

Equation 3.9-12

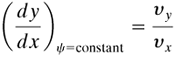
Also, for lines of constant φ,

Equation 3.9-13

Equation 3.9-14

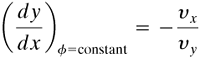
Hence,

Equation 3.9-15

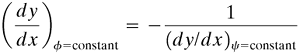
An example of the use of the stream function is in obtaining the flow pattern for inviscid, irrotational flow past a cylinder of infinite length. The fluid approaching the cylinder has a steady and uniform velocity of v_∞ in the x direction. Laplace's equation (3.9-10) can be converted to cylindrical coordinates to give

Equation 3.9-16

where the velocity components are given by

Equation 3.9-17

Using four boundary conditions which are needed and the method of separation of variables, the stream function ψ is obtained. Converting to rectangular coordinates,

Equation 3.9-18

where R is the cylinder radius. The streamlines and the constant-velocity-potential lines are plotted in Fig. 3.9-2 as a flow net.

EXAMPLE 3.9-2. Stream Function for a Flow Field The velocity components for a flow field are as follows: Prove that it satisfies the conservation of mass and determine ψ. Solution: First we determine ∂vx/∂x = 2ax and ∂vy/∂y = -2ax. Substituting these values into Eq. (3.6-24), the conservation of mass for two-dimensional flow, Then using Eq. (3.9-1), Equation 3.9-19 Integrating Eq. (3.9-19) for vx, Equation 3.9-20 Integrating Eq. (3.9-19) for vy, Equation 3.9-21 Equating Eq. (3.9-20) to (3.9-21), Equation 3.9-22 Canceling like terms, Equation 3.9-23 Hence, f(x) = 0 and f(y) = ay3/3. Substituting f(x) = 0 into Eq. (3.9-20), Equation 3.9-24

EXAMPLE 3.9-3. Stream Function and Velocities from Potential Function The potential function for a two-dimensional, irrotational, incompressible flow field is given as ϕ = x2 − 2y - y2. Find the stream function ψ and the velocity components vx and vy. Solution: Using Eqs. (3.9-1) and (3.9-5), Combining, Equation 3.9-25 Differentiating the potential function with respect to x and equating the result to ∂ψ/∂y from Eq. (3.9-25), Equation 3.9.26 Differentiating the potential function with respect to y and equating the result to -∂ψ/∂x from Eq. (3.9-25), Equation 3.9-27 Integrating Eq. (3.9-26), Equation 3.9-28 Integrating Eq. (3.9-27), Equation 3.9-29 Equating Eq. (3.9-28) to (3.9-29), Equation 3.9-30 Hence, after canceling 2xy from both sides, Equation 3.9-31 Therefore, f(x) = 2x and f(y) = 0. Substituting f(x) = 2x into Eq. (3.9-28), Equation 3.9-32 The velocities are, from Eqs. (3.9-26) and (3.9-27), Equation 3.9-33 In potential flow, the stream function and potential function are used to represent the flow in the main body of the fluid. These ideal fluid solutions do not satisfy the condition that νx = νy = 0 on the wall surface. Near the wall we have viscous drag and we use boundary-layer theory, where we obtain approximate solutions for the velocity profiles in this thin boundary layer taking into account viscosity. This is discussed in Section 3.10. Then we splice this solution onto the ideal flow solution that describes flow outside the boundary layer.

3.9E. Differential Equations of Motion for Creeping Flow

At very low Reynolds numbers, below about 1, the term creeping flow is used to describe flow at very low velocities. This type of flow applies for the fall or settling of small particles through a fluid. Stokes' law is derived using this type of flow in problems of settling and sedimentation.

In flow around a sphere, for example, the fluid changes velocity and direction in a complex manner. If the inertia effects in this case were important, it would be necessary to keep all the terms in the three Navier-Stokes equations. Experiments show that at a Reynolds number below about 1, the inertia effects are small and can be omitted. Hence, the equations of motion, Eqs. (3.7-36)-(3.7-38) for creeping flow of an incompressible fluid, become

Equation 3.9-34

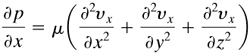
Equation 3.9-35

Equation 3.9-36

For flow past a sphere the stream function ψ can be used in the Navier-Stokes equation in spherical coordinates to obtain the equation for the stream function and the velocity distribution and pressure distribution over the sphere. Then by integration over the whole sphere, the form drag, caused by the pressure distribution, and the skin friction or viscous drag, caused by the shear stress at the surface, can be summed to give the total drag:

Equation 3.9-37

where F_D is total drag force in N, D_p is particle diameter in m, ν is free stream velocity of fluid approaching the sphere in m/s, and μ is viscosity in kg/m · s. This is Stokes' equation for the drag force on a sphere.

Often Eq. (3.9-37) is rewritten as follows:

Equation 3.9-38

where C_D is a drag coefficient, equal to 24/N_Re for Stokes' law, and A is the projected area of the sphere, . This is discussed in more detail in Section 3.1 for flow past spheres.