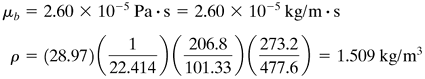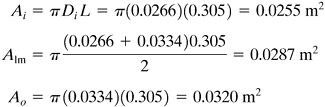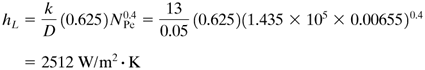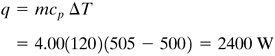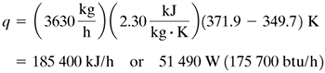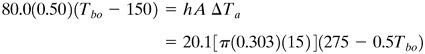4.5. FORCED CONVECTION HEAT TRANSFER INSIDE PIPES

4.5A. Introduction and Dimensionless Numbers

In most situations involving a liquid or a gas in heat transfer, convective heat transfer usually occurs as well as conduction. In most industrial processes where heat transfer is occurring, heat is being transferred from one fluid through a solid wall to a second fluid. In Fig. 4.5-1 heat is being transferred from the hot flowing fluid to the cold flowing fluid. The temperature profile is shown.

The velocity gradient, when the fluid is in turbulent flow, is very steep next to the wall in the thin viscous sublayer where turbulence is absent. Here the heat transfer is mainly by conduction, with a large temperature difference of T₂ − T₃ in the warm fluid. As we move farther away from the wall, we approach the turbulent region, where rapidly moving eddies tend to equalize the temperature. Hence, the temperature gradient is less and the difference T₁ − T₂ is small. The average temperature of fluid A is slightly less than the peak value T₁. A similar explanation can be given for the temperature profile in the cold fluid.

The convective coefficient for heat transfer through a fluid is given by

Equation 4.5-1

where h is the convective coefficient in W/m² · K, A is the area in m², T is the bulk or average temperature of the fluid in K, T_w is the temperature of the wall in contact with the fluid in K, and q is the heat-transfer rate in W. In English units, q is in btu/h, h in btu/h · ft² · °F, A in ft², and T and T_w in °F.

The type of fluid flow, whether laminar or turbulent, of the individual fluid has a great effect on the heat-transfer coefficient h, which is often called a film coefficient, since most of the resistance to heat transfer is in a thin film close to the wall. The more turbulent the flow, the greater the heat-transfer coefficient.

There are two main classifications of convective heat transfer. The first is free or natural convection, where the motion of the fluid results from the density changes in heat transfer. The buoyant effect produces a natural circulation of the fluid, so it moves past the solid surface. In the second type, forced convection, the fluid is forced to flow by pressure differences, a pump, a fan, and so on.

Most of the correlations for predicting film coefficients h are semiempirical in nature and are affected by the physical properties of the fluid, the type and velocity of flow, the temperature difference, and the geometry of the specific physical system. Some approximate values for convective coefficients were presented in Table 4.1-2. In the following correlations, either SI or English units can be used, since the equations are dimensionless.

To correlate these data for heat-transfer coefficients, dimensionless numbers such as the Reynolds and Prandtl numbers are used. The Prandtl number is the ratio of the shear component of diffusivity for momentum μ/ρ to the diffusivity for heat k/ρc_p and physically relates the relative thicknesses of the hydrodynamic layer and thermal boundary layer:

Equation 4.5-2

Values of the N_Pr for gases are given in Appendix A.3 and range from about 0.5 to 1.0. Values for liquids range from about 2 to well over 10⁴. The dimensionless Nusselt number, N_Nu, is used to relate data for the heat-transfer coefficient h to the thermal conductivity k of the fluid and a characteristic dimension D:

Equation 4.5-3

For example, for flow inside a pipe, D is the diameter.

4.5B. Heat-Transfer Coefficient for Laminar Flow Inside a Pipe

Certainly, the most important convective heat-transfer process industrially is that of cooling or heating a fluid flowing inside a closed circular conduit or pipe. Different types of correlations for the convective coefficient are needed for laminar flow (N_Re below 2100), for fully turbulent flow (N_Re above 6000), and for the transition region (N_Re between 2100 and 6000).

For laminar flow of fluids inside horizontal tubes or pipes, the following equation of Sieder and Tate (S1) can be used for N_Re < 2100:

Equation 4.5-4

where D = pipe diameter in m, L = pipe length before mixing occurs in the pipe in m, μ_b = fluid viscosity at bulk average temperature in Pa · s, μ_w = viscosity at the wall temperature, c_p = heat capacity in J/kg · K, k = thermal conductivity in W/m · K, h_a = average heat-transfer coefficient in W/m² · K, and N_Nu = dimensionless Nusselt number. All the physical properties are evaluated at the bulk fluid temperature except μ_w. The Reynolds number is

Equation 4.5-5

and the Prandtl number,

Equation 4.5-6

This equation holds for (N_ReN_PrD/L) > 100. If used down to (N_ReN_PrD/L) > 10, it still holds to ±20% (B1). For (N_ReN_PrD/L) < 100, another expression is available (P1).

In laminar flow the average coefficient h_a depends strongly on heated length. The average (arithmetic mean) temperature drop ΔT_a is used in the equation to calculate the heat-transfer rate q:

Equation 4.5-7

where T_w is the wall temperature in K, T_bi the inlet bulk fluid temperature, and T_bo the outlet bulk fluid temperature.

For large pipe diameters and large temperature differences ΔT between pipe wall and bulk fluid, natural convection effects can increase h (P1). Equations are also available for laminar flow in vertical tubes.

4.5C. Heat-Transfer Coefficient for Turbulent Flow Inside a Pipe

When the Reynolds number is above 6000, the flow is fully turbulent. Since the rate of heat transfer is greater in the turbulent region, many industrial heat-transfer processes are in the turbulent region.

The following equation has been found to hold for tubes but is also used for pipes. It holds for a N_Re > 6000, a N_Pr between 0.7 and 16 000, and L/D > 60.

Equation 4.5-8

where h_L is the heat-transfer coefficient based on the log mean driving force ΔT_lm (see Section 4.5H). The fluid properties except for μ_w are evaluated at the mean bulk temperature. If the bulk fluid temperature varies from the inlet to the outlet of the pipe, the mean of the inlet and outlet temperatures is used. For an LID < 60, where the entry is an abrupt contraction, an approximate correction is provided by multiplying the right-hand side of Eq. (4.5-8) by a correction factor given in Section 4.5F.

The use of Eq. (4.5-8) may be trial and error, since the value of h_L must be known in order to evaluate T_w, and hence μ_w, at the wall temperature. Also, if the mean bulk temperature increases or decreases in the tube length L because of heat transfer, the bulk temperature at length L must be estimated in order to have a mean bulk temperature of the entrance and exit to use.

The heat-transfer coefficient for turbulent flow is somewhat greater for a pipe than for a smooth tube. This effect is much less than in fluid friction, and it is usually neglected in calculations. Also, for liquid metals that have Prandtl numbers << 1, other correlations must be used to predict the heat-transfer coefficient. (See Section 4.5G.) For shapes of tubes other than circular, the equivalent diameter can be used, as discussed in Section 4.5E.

For air at 1 atm total pressure, the following simplified equation holds for turbulent flow in pipes:

Equation 4.5-9

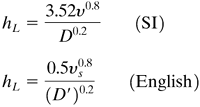
where D is in m, ν in m/s, and h_L in W/m² · K for SI units; and D' is in in., ν_s in ft/s, and h_L in btu/h · ft² · °F for English units.

Water is often used in heat-transfer equipment. A simplified equation to use for a temperature range of T = 4−105°C (40−220°F) is

Equation 4.5-10

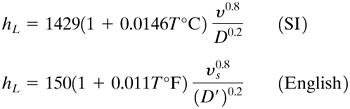
For organic liquids, a very simplified equation to use for approximations is as follows (P3):

Equation 4.5-11

For flow inside helical coils and N_Re above 10⁴, the predicted film coefficient for straight pipes should be increased by the factor (1 + 3.5D/D_coil).

EXAMPLE 4.5-1. Heating of Air in Turbulent Flow Air at 206.8 kPa and an average of 477.6 K is being heated as it flows through a tube of 25.4 mm inside diameter at a velocity of 7.62 m/s. The heating medium is 488.7 K steam condensing on the outside of the tube. Since the heat-transfer coefficient of condensing steam is several thousand W/m2 · K and the resistance of the metal wall is very small, it will be assumed that the surface wall temperature of the metal in contact with the air is 488.7 K. Calculate the heat-transfer coefficient for an L/D > 60 and also the heat-transfer flux q/A. Solution: From Appendix A.3, for physical properties of air at 477.6 K (204.4°C), μb = 2.60 × 10-5 Pa · s, k = 0.03894 W/m, NPr = 0.686. At 488.7 K (215.5°C), μw = 2.64 × KT5 Pa · s. The Reynolds number calculated at the bulk fluid temperature of 477.6 K is Hence, the flow is turbulent and Eq. (4.5-8) will be used. Substituting into Eq. (4.5-8), Solving, hL = 63.2 W/m2 · K (11.13 btu/h · ft2 · °F). To solve for the flux q/A,

4.5D. Heat-Transfer Coefficient for Transition Flow Inside a Pipe

In the transition region for a N_Re between 2100 and 6000, the empirical equations are not well defined, just as in the case of fluid friction factors. No simple equation exists for accomplishing a smooth transition from heat transfer in laminar flow to that in turbulent flow, that is, a transition from Eq. (4.5-4) at a N_Re = 2100 to Eq. (4.5-8) at a N_Re = 6000.

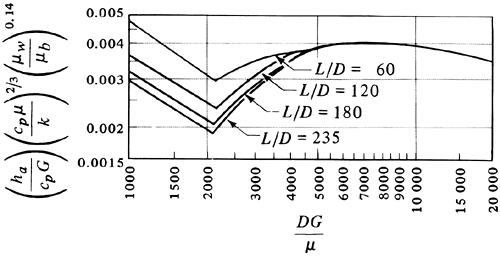
The plot in Fig. 4.5-2 represents an approximate relationship to use between the various heat-transfer parameters and the Reynolds number between 2100 and 6000. For below a N_Re, of 2100, the curves represent Eq. (4.5-4), and above 10⁴, Eq. (4.5-8). The mean ΔT_a of Eq. (4.5-7) should be used with the h_a in Fig. 4.5-2.

4.5E. Heat-Transfer Coefficient for Noncircular Conduits

A heat-transfer system often used is one in which fluids flow at different temperatures in concentric pipes. The heat-transfer coefficient of the fluid in the annular space can be predicted by using the same equations as for circular pipes. However, the equivalent diameter defined in Section 2.10G must be used. For an annular space, D_eq is the ID of the outer pipe D₁ minus the OD of the inner pipe D₂. For other geometries, an equivalent diameter can also be used.

EXAMPLE 4.5-2. Water Heated by Steam and Trial-and-Error Solution Water is flowing in a horizontal 1-in. schedule 40 steel pipe at an average temperature of 65.6°C and a velocity of 2.44 m/s. It is being heated by condensing steam at 107.8°C on the outside of the pipe wall. The steam-side coefficient has been estimated as h0 = 10 500 W/m2 · K. Calculate the convective coefficient hi for water inside the pipe. Calculate the overall coefficient Ui based on the inside surface area. Calculate the heat-transfer rate q for 0.305 m of pipe with the water at an average temperature of 65.6°C. Solution: From Appendix A.5, the various dimensions are Di = 0.0266 m and D0 = 0.0334 m. For water at a bulk average temperature of 65.6°C, from Appendix A.2, NPr = 2.72, ρ = 0.980(1000) = 980 kg/m3, k = 0.633 W/m · K, and μ = 4.32 × 10-4 Pa · S = 4.32 × 10-4 kg/m · s. The temperature of the inside metal wall is needed and will be assumed as about one-third the difference between 65.6 and 107.8, or 80°C = Tw, for the first trial. Hence, μw at 80°C = 3.56 × 10-4 Pa · s. First, the Reynolds number of the water is calculated at the bulk average temperature: Hence, the flow is turbulent. Using Eq. (4.5-8) and substituting known values, Solving, hL = hi = 13 324 W/m2 · K. For part (b), the various areas are as follows for 0.305-m pipe: The k for steel is 45.0 W/m · K. The resistances are The overall temperature difference is (107.8 - 65.6)°C = 42.2°C = 42.2 K. The temperature drop across the water film is Hence, Tw = 65.6 + 14.5 = 80.1°C. This is quite close to the original estimate of 80°C. The only physical property changing in the second estimate would be μw. This would have a negligible effect on hi, and a second trial is not necessary. For part (b), the overall coefficient is, by Eq. (4.3-16), For part (c), with the water at an average temperature of 65.6°C,

4.5F. Entrance-Region Effect on Heat-Transfer Coefficient

Near the entrance of a pipe where the fluid is being heated, the temperature profile is not fully developed and the local coefficient h is greater than the fully developed heat-transfer coefficient h_L for turbulent flow. At the entrance itself, where no temperature gradient has been established, the value of h is infinite. The value of h drops rapidly and is approximately the same as h_L at L/D ≅ 60, where L is the entrance length. These relations for turbulent flow inside a pipe are as follows where the entrance is an abrupt contraction:

Equation 4.5-12

Equation 4.5-13

where h is the average value for a tube of finite length L and h_L is the value for a very long tube.

4.5G. Liquid-Metals Heat-Transfer Coefficient

Liquid metals are sometimes used as heat-transfer fluids in cases where a fluid is needed over a wide temperature range at relatively low pressures. Liquid metals are often used in nuclear reactors and have high heat-transfer coefficients as well as a high heat capacity per unit volume. The high heat-transfer coefficients are due to the very high thermal conductivities and, hence, low Prandtl numbers. In liquid metals in pipes, heat transfer by conduction is very important in the entire turbulent core because of the high thermal conductivity and is often more important than the convection effects.

For fully developed turbulent flow in tubes with uniform heat flux, the following equation can be used (L1):

Equation 4.5-14

where the Peclet number N_Pe = N_ReN_Pr. This holds for L/D > 60 and N_Pe between 100 and 10⁴. For constant wall temperatures,

Equation 4.5-15

for L/D > 60 and N_Pe > 100. All physical properties are evaluated at the average bulk temperature.

EXAMPLE 4.5-3. Liquid-Metal Heat Transfer Inside a Tube A liquid metal flows at a rate of 4.00 kg/s through a tube having an inside diameter of 0.05 m. The liquid enters at 500 K and is heated to 505 K in the tube. The tube wall is maintained at a temperature of 30 K above the fluid bulk temperature and constant heat flux is also maintained. Calculate the required tube length. The average physical properties are as follows: μ = 7.1 × 10-4 Pa · s, ρ = 7400 kg/m3, cp = 120 J/kg · K, k = 13 W/m · K. Solution: The area is A = πD2/4 = π(0.05)2/4 = 1.963 × 10–3 m2. Then G = 4.0/1.963 × 10–3 = 2.038 × 103 kg/m2 · s. The Reynolds number is Using Eq. (4.5-14), Using a heat balance, Equation 4.5-16 Substituting into Eq. (4.5-1), Hence, A = 2400/75 360 = 3.185 × 10-2 m2. Then, Solving, L = 0.203 m.

4.5H. Log Mean Temperature Difference and Varying Temperature Drop

Equations (4.5-1) and (4.3-12) as written apply only when the temperature drop (T_i − T₀) is constant for all parts of the heating surface. Hence, the equation

Equation 4.5-17

only holds at one point in the apparatus when the fluids are being heated or cooled. However, as the fluids travel through the heat exchanger, they become heated or cooled and either T_i or T₀ or both vary. Then (T_i − T₀) or ΔT varies with position, and some mean ΔT_m must be used over the whole apparatus.

In a typical heat exchanger, a hot fluid inside a pipe is cooled from to by a cold fluid which is flowing on the outside in a double pipe countercurrently (in the reverse direction) and is heated from T₂ to T₁, as shown in Fig. 4.5-3a. The ΔT shown is varying with distance. Hence, ΔT in Eq. (4.5-17) varies as the area A goes from 0 at the inlet to A at the outlet of the exchanger.

For countercurent flow of the two fluids as in Fig. 4.5-3a, the heat-transfer rate is

Equation 4.5-18

where ΔT_m is a suitable mean temperature difference to be determined. For a dA area, a heat balance on the hot and the cold fluids gives

Equation 4.5-19

where m is flow rate in kg/s. The values of m, m', c_p, , and U are assumed constant. Also,

Equation 4.5-20

From Eq. (4.5-19), dT' = -dq/ and dT = dq/mc_p. Then,

Equation 4.5-21

Substituting Eq. (4.5-20) into (4.5-21),

Equation 4.5-22

Integrating between points 1 and 2,

Equation 4.5-23

Making a heat balance between the inlet and outlet,

Equation 4.5-24

Solving for and mc_p in Eq. (4.5-24) and substituting into Eq. (4.5-23),

Equation 4.5-25

Comparing Eqs. (4.5-18) and (4.5-25), we see that ΔT_m is the log mean temperature difference ΔT_lm. Hence, in the case where the overall heat-transfer coefficient U is constant throughout the equipment and the heat capacity of each fluid is constant, the proper temperature driving force to use over the entire apparatus is the log mean driving force,

Equation 4.5-26

where

Equation 4.5-27

It can be also shown that for parallel flow, as pictured in Fig. 4.5-3b, the log mean temperature difference should be used. In some cases, where steam is condensing, and may be the same. The equations still hold for this case. When U varies with distance or other complicating factors occur, other references should be consulted (B2, P3, W1).

EXAMPLE 4.5-4. Heat-Transfer Area and Log Mean Temperature Difference A heavy hydrocarbon oil which has a cpm = 2.30 kJ/kg · K is being cooled in a heat exchanger from 371.9 K to 349.7 K and flows inside the tube at a rate of 3630 kg/h. A flow of 1450 kg water/h enters at 288.6 K for cooling and flows outside the tube. Calculate the water outlet temperature and heat-transfer area if the overall Ui = 340 W/m2 · K and the streams are countercurrent. Repeat for parallel flow. Solution: Assume a cpm = 4.187 kJ/kg · K for water. The water inlet T2 = 288.6 K, outlet = T1; oil inlet = 371.9, outlet = 349.7 K. Calculating the heat lost by the oil, By a heat balance, the q must also equal the heat gained by the water: Solving, T1 = 319.1 K. To solve for the log mean temperature difference, ΔT2 = − T2 = 349.7 − 288.6 = 61.1 K, ΔT1 = - T1 = 371.9 - 319.1 = 52.8 K. Substituting into Eq. (4.5-27), Using Eq. (4.5-26), Solving, Ai = 2.66 m2. For part (b), the water outlet is still T1 = 319.1 K. Referring to Fig. 4.5-3b, ΔT2 = 371.9 − 288.6 = 83.3K and ΔT1 = 349.7 - 319.1 = 30.6 K. Again, using Eq. (4.5-27) and solving, ΔTlm = 52.7 K. Substituting into Eq. (4.5-26), Ai = 2.87 m2. This is a larger area than for counterflow. This occurs because counterflow gives larger temperature driving forces, and it is usually preferred over parallel flow for this reason.

EXAMPLE 4.5-5. Laminar Heat Transfer and Trial and Error A hydrocarbon oil at 150°F enters inside a pipe with an inside diameter of 0.0303 ft and a length of 15 ft with a flow rate of 80 lbm/h. The inside pipe surface is assumed constant at 350°F, since steam is condensing outside the pipe wall, and has a very large heat-transfer coefficient. The properties of the oil are cpm = 0.50 btu/lbm · °F and km = 0.083 btu/h · ft · °F. The viscosity of the oil varies with temperature as follows: 150°F, 6.50 cp; 200°F, 5.05 cp; 250°F, 3.80 cp; 300°F, 2.82 cp; 350°F, 1.95 cp. Predict the heat-transfer coefficient and the oil outlet temperature, Tbo. Solution: This is a trial-and-error solution since the outlet temperature of the oil Tbo is unknown. The value of Tbo = 250°F will be assumed and checked later. The bulk mean temperature of the oil to use for the physical properties is (150 + 250)/2 or 200°F. The viscosity at 200°F is At the wall temperature of 350°F, The cross-section area of the pipe A is The Reynolds number at the bulk mean temperature is The Prandtl number is Since the NRe is below 2100, the flow is in the laminar region and Eq. (4.5-4) will be used. Even at the outlet temperature of 250°F, the flow is still laminar. Substituting, Solving, ha = 20.1 btu/h · ft2 · °F (114 W/m2 · K). Next, making a heat balance on the oil, Equation 4.5-28 Using Eq. (4.5-7) Equation 4.5-7 For ΔTa, Equating Eq. (4.5-28) to (4.5-7) and substituting, Solving, Tbo = 255°F. This is higher than the assumed value of 250°F. For the second trial, the mean bulk temperature of the oil would be (150 + 255)/2 or 202.5°F. The new viscosity is 5.0 cp compared with 5.05 for the first estimate. This only affects the (μb/μw)0.14 factor in Eq. (4.5-4), since the viscosity effect in the (NRe)(NPr) factor cancels out. The heat-transfer coefficient will change by less than 0.2%, which is negligible. Hence, the outlet temperature of T1 = 255°F (123.9°C) is correct.