4.14. DIMENSIONAL ANALYSIS IN HEAT TRANSFER
4.14A. Introduction
As seen in many of the correlations for fluid flow and heat transfer, many dimensionless groups, such as the Reynolds number and Prandtl number, occur in these correlations. Dimensional analysis is often used to group the variables in a given physical situation into dimensionless parameters or numbers which can be useful in experimentation and correlating data.
An important way of obtaining these dimensionless groups is to use dimensional analysis of differential equations as described in Section 3.11. Another useful method is the Buckingham method, in which the listing of the significant variables in the particular physical problem is done first. Then we determine the number of dimensionless parameters into which the variables may be combined.
4.14B. Buckingham Method
1. Heat transfer inside a pipe
The Buckingham theorem, given in Section 3.11, states that the function relationship among q quantities or variables whose units may be given in terms of u fundamental units or dimensions may be written as (q –u) dimensionless groups.
As an additional example to illustrate the use of this method, let us consider a fluid flowing in turbulent flow at velocity v inside a pipe of diameter D and undergoing heat transfer to the wall. We wish to predict the dimensionless groups relating the heat-transfer coefficient h to the variables D, ρ, μ, cp, k, and v. The total number of variables is q = 7.
The fundamental units or dimensions are u = 4 and are mass M, length L, time t, and temperature T. The units of the variables in terms of these fundamental units are as follows:
![]()
Hence, the number of dimensionless groups or π's can be assumed to be 7 – 4, or 3. Then
Equation 4.14-1
![]()
We will choose the four variables D, k, μ, and v to be common to all the dimensionless groups. Then the three dimensionless groups are
Equation 4.14-2
![]()
Equation 4.14-3
![]()
Equation 4.14-4
![]()
For π1, substituting the actual dimensions,
Equation 4.14-5

Summing for each exponent,
Equation 4.14-6

Solving these equations simultaneously, a = 1, b = 0, c = -1, and d = 1.
Substituting these values into Eq. (4.14-2),
Equation 4.14-7
![]()
Repeating for π2 and π 3 and substituting the actual dimensions,
Equation 4.14-8
![]()
Equation 4.14-9
![]()
Substituting π1, π2, and π3 into Eq. (4.14-1) and rearranging,
Equation 4.14-10
![]()
This is in the form of the familiar equation for heat transfer inside pipes, Eq. (4.5-8).
This type of analysis is useful in empirical correlations of heat-transfer data. The importance of each dimensionless group, however, must be determined by experimentation (B1, M1).
2. Natural convection heat transfer outside a vertical plane
In the case of natural convection heat transfer from a vertical plane wall of length L to an adjacent fluid, different dimension-less groups should be expected as compared to forced convection inside a pipe, since velocity is not a variable. The buoyant force due to the difference in density between the cold and the heated fluid should be a factor. As seen in Eqs. (4.7-1) and (4.7-2), the buoyant force depends upon the variables β, g, ρ, and ΔT. Hence, the list of variables to be considered and their fundamental units are as follows:
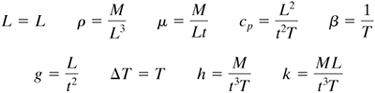
The number of variables is q = 9. Since u = 4, the number of dimensionless groups or π's is 9 - 4, or 5. Then π1 = f(π2, π3, π4,π5).
We will choose the four variables L, μ, k, and g to be common to all the dimensionless groups:

For π1, substituting the dimensions,
Equation 4.14-11
![]()
Solving for the exponents as before, ![]() , b = -1, c = 0, and
, b = -1, c = 0, and ![]() . Then π1 becomes
. Then π1 becomes
Equation 4.14-12
![]()
Taking the square of both sides to eliminate fractional exponents,
Equation 4.14-13
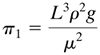
Repeating for the other π equations,
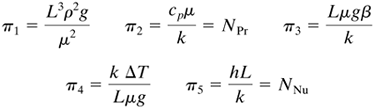
Combining the dimensionless groups π1, π3, and π4 as follows,
Equation 4.14-14
![]()
Equation (4.14-14) is the Grashof group given in Eq. (4.7-4). Hence,
Equation 4.14-15
![]()
