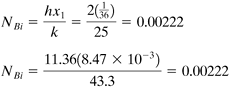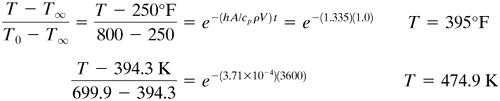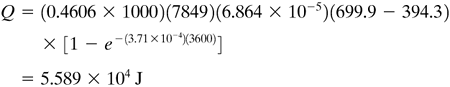5.2. SIMPLIFIED CASE FOR SYSTEMS WITH NEGLIGIBLE INTERNAL RESISTANCE

5.2A. Basic Equation

We begin our treatment of transient heat conduction by analyzing a simplified case. In this situation we consider a solid which has a very high thermal conductivity or very low internal conductive resistance compared to the external surface resistance, where convection occurs from the external fluid to the surface of the solid. Since the internal resistance is very small, the temperature within the solid is essentially uniform at any given time.

An example would be a small, hot cube of steel at T₀ K at time t = 0, suddenly immersed in a large bath of cold water at T_∞ which is held constant with time. Assume that the heat-transfer coefficient h in W/m² · K is constant with time. Making a heat balance on the solid object for a small time interval of time dt s, the heat transfer from the bath to the object must equal the change in internal energy of the object:

Equation 5.2-1

where A is the surface area of the object in m², T the average temperature of the object at time t in s, ρ the density of the object in kg/m³, and V the volume in m³. Rearranging the equation and integrating between the limits of T = T₀ when t = 0 and T = T when t = t,

Equation 5.2-2

Equation 5.2-3

This equation describes the time–temperature history of the solid object. The term c_p ρV is often called the lumped thermal capacitance of the system. This type of analysis is often called the lumped capacity method or Newtonian heating or cooling method.

5.2B. Equation for Different Geometries

In using Eq. (5.2-3) the surface/volume ratio of the object must be known. The basic assumption of negligible internal resistance was made in the derivation. This assumption is reasonably accurate when

Equation 5.2-4

where hx₁/k is called the Biot number N_Bi, which is dimensionless, and x₁ is a characteristic dimension of the body obtained from x₁ = V/A. The Biot number compares the relative values of internal conduction resistance and surface convective resistance to heat transfer.

For a sphere,

Equation 5.2-5

For a long cylinder,

Equation 5.2-6

For a long square rod,

Equation 5.2-7

EXAMPLE 5.2-1. Cooling of a Steel Ball A steel ball having a radius of 1.0 in. (25.4 mm) is at a uniform temperature of 800°F (699.9 K). It is suddenly plunged into a medium whose temperature is held constant at 250°F (394.3 K). Assuming a convective coefficient of h = 2.0 btu/h · ft2 · °F (11.36 W/m2 · K), calculate the temperature of the ball after 1 h (3600 s). The average physical properties are k = 25 btu/h · ft · °F (43.3 W/m · K), ρ = 490 lbm/ft3 (7849 kg/m3), and cp = 0.11 btu/lbm · °F (0.4606 kJ/kg · K). Use SI and English units. Solution: For a sphere from Eq. (5.2-5), From Eq. (5.2-4) for the Biot number, This value is <0.1; hence, the lumped capacity method can be used. Then, Substituting into Eq. (5.2-3) for t = 1.0 h and solving for T,

5.2C. Total Amount of Heat Transferred

The temperature of the solid at any time t can be calculated from Eq. (5.2-3). At any time t, the instantaneous rate of heat transfer q(t) in W from the solid of negligible internal resistance can be calculated from

Equation 5.2-8

Substituting the instantaneous temperature T from Eq. (5.2-3) into Eq. (5.2-8),

Equation 5.2-9

To determine the total amount of heat Q in W · s or J transferred from the solid from time t = 0 to t = t, we can integrate Eq. (5.2-9):

Equation 5.2-10

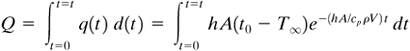
Equation 5.2-11

EXAMPLE 5.2-2. Total Amount of Heat in Cooling For the conditions in Example 5.2-1, calculate the total amount of heat removed up to time t = 3600 s. Solution: From Example 5.2-1, hA/cpρV = 3.71 × 10−4 s−1. Also, V = 4πr3/3 = 4(π)(0.0254)3/3 = 6.864 × 10−5 m3. Substituting into Eq. (5.2-11),