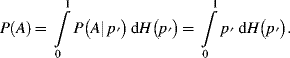2
Probabilistic Approaches for Treating Uncertainty
Probability has been, and continues to be, a fundamental concept in the context of risk assessment. Unlike the other measures of uncertainty considered in this book, probability is a single-valued measure.
The common axiomatic basis of probability is found in Kolmogorov's (1933) probability axioms. Let 
denote events in a sample space 
. The following probability axioms are assumed to hold:
(2.1)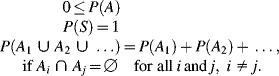 
These axioms specify that probability is a non-negative, normalized, and additive measure.
Different types of operational or conceptual interpretations of probability can be distinguished. Among the most common are:
- Classical
- Relative frequency
- Subjective
- Logical.
Modern probability theory is not based on a particular interpretation of probability, although its standard language is best suited to the classical and relative frequency interpretations (Aven, 2012). In the context of risk assessment, the relative frequency and subjective interpretations are most common. Relative frequency probability is broadly recognized as the proper representation of variation in large populations (aleatory uncertainty), also among proponents of alternative representations of uncertainty; see, for example, Baudrit, Dubois, and Guyonnet (2006) and Ferson and Ginzburg (1996). The subjective interpretation, where probability is understood as expressing a degree of belief and measuring epistemic uncertainty, is also widely applied in risk assessment (Bedford and Cooke, 2001). The classical and logical interpretations of probability have less relevance in the context of risk assessment, as will be seen in the coming sections where we review and discuss the interpretations mentioned above. The review, which to a large extent is taken from or based on Aven (2013a), covers also the Bayesian subjective probability framework, which through the concept of chance provides a link between subjective probability and limiting relative frequencies.
2.1 Classical Probabilities
The classical interpretation of probability dates back to de Laplace (1812). It applies only in situations involving a finite number of outcomes which are equally likely to occur. The probability of an event 
is equal to the ratio between the number of outcomes resulting in 
and the total number of possible outcomes, that is,
(2.2) 
Consider as an example the tossing of a die. Then 
, as there are six possible outcomes which are equally likely to appear and only one outcome which gives the event that the die shows “1.” The requirement for each outcome to be equally likely is crucial for the understanding of this interpretation and has been subject to much discussion in the literature. A common perspective taken is that this requirement is met if there is no evidence favoring some outcomes over others. This is the so-called “principle of indifference,” also sometimes referred to as the “principle of insufficient reason.” In other words, classical probabilities are appropriate when the evidence, if there is any, is symmetrically balanced (Hajek, 2001), such as we may have when throwing a die or playing a card game.
The classical interpretation is, however, not applicable in most real-life situations beyond random gambling and sampling, as we seldom have a finite number of outcomes which are equally likely to occur. The discussion about the principle of indifference is interesting from a theoretical point of view, but a probability concept based solely on this principle is not so relevant in a context where we search for a concept of probability that can be used in a wide range of applications.
2.2 Frequentist Probabilities
The frequentist probability of an event 
, denoted 
, is defined as the fraction of times event 
occurs if the situation/experiment considered were repeated (hypothetically) an infinite number of times. Thus, if an experiment is performed 
times and event 
occurs 
times out of these, then 
is equal to the limit of 
as 
tends to infinity (tacitly assuming that the limit exists), that is,
(2.3) 
Taking a sample of repetitions of the experiment, event 
occurs in some of the repetitions and not in the rest. This phenomenon is attributed to “randomness,” and asymptotically the process generates a fraction of successes, the “true” probability 
, which describes quantitatively the aleatory uncertainty (i.e., variation) about the occurrence of event 
. In practice, it is of course not possible to repeat a situation an infinite number of times. The probability 
is a model concept used as an approximation to a real-world setting where the population of units or number of repetitions is always finite. The limiting fraction 
is typically unknown and needs to be estimated by the fraction of occurrences of 
in the finite sample considered, producing an estimate 
.
A frequentist probability is thus a mind-constructed quantity – a model concept founded on the law of large numbers which says that frequencies 
converge to a limit under certain conditions: that is, the probability of event 
exists and is the same in all experiments, and the experiments are independent. These conditions themselves appeal to probability, generating a problem of circularity. One approach to deal with this problem is to assign the concept of probability to an individual event by embedding the event into an infinite class of “similar” events having certain “randomness” properties (Bedford and Cooke, 2001, p. 23). This leads to a somewhat complicated framework for understanding the concept of probability; see the discussion in van Lambalgen (1990). Another approach, and a common way of looking at probability, is to simply assume the existence of the probability 
, and then refer to the law of large numbers to give 
the limiting relative frequency interpretation. Starting from Kolmogorov's axioms (as in the second paragraph of the introduction to Part II; see also Bedford and Cooke 2001, p. 40) and the concept of conditional probability, as well as presuming the existence of probability, the theory of probability is derived, wherein the law of large numbers constitutes a key theorem which provides the interpretation of the probability concept.
The so-called propensity interpretation is yet another way of justifying the existence of a probability (SEP, 2009). This interpretation specifies that probability should primarily be thought of as a physical characteristic: The probability is a propensity of a repeatable experimental set-up which produces outcomes with limiting relative frequency 
. Consider as an example a coin. The physical characteristics of the coin (weight, center of mass, etc.) are such that when tossing the coin over and over again the fraction of heads will be p (Figure 2.1). The literature on probability shows that the existence of a propensity is controversial (Aven, 2013a). However, from a conceptual point of view the idea of a propensity may be no more difficult to grasp than the idea of an infinite number of repetitions of experiments. If the framework of frequentist probability is accepted, that is, if referring to an infinite sequence of similar situations makes sense, the propensity concept should also be accepted as it essentially expresses that such a framework exists.
Figure 2.1 Repetition of the experiment of tossing a coin.
Thus, for gambling situations and when dealing with fractions in large populations of similar items, the frequentist probability concept makes sense, as a model concept. Of course, if a die is thrown over and over again a very large number of times its physical properties will eventually change, so the idea of “similar experiments” is questionable. Nevertheless, for all practical purposes we can carry out (in theory) a large number of trials, say 100 000, without any physical changes in the experimental set-up, and that is what is required for the concept to be meaningful. The same is true if we consider a population of (say) 100 000 human beings belonging to a specific category, say men in the age range 20 to 30 years old in a specific country.
It is not surprising, then, that frequency probabilities are so commonly and widely adopted in practice. The theoretical concept of a frequentist probability is introduced, often in the form of a probability model – for example, the binomial, normal (Gaussian), or Poisson distributions – and statistical analysis is carried out to estimate the frequentist probabilities (more generally the parameters of the probability models) and to study the properties of the estimators using well-established statistical theory. However, the types of situations that are captured by this framework are limited. As noted by Singpurwalla (2006, p. 17), the concept of frequency probabilities “is applicable to only those situations for which we can conceive of a repeatable experiment.” This excludes many situations and events. Consider for example events such as the rise of sea level over the next 20 years, the guilt or innocence of an accused individual, or the occurrence or not of a disease in a specific person with a specific history.
What does it mean that the situations under consideration are “similar?” The “experimental conditions” cannot be identical, since we would then observe exactly the same outcome and the ratio 
would be either 1 or 0. What kind of variation between the experiments is allowed? This is often difficult to specify and makes it challenging to extend frequentist probabilities to include real-life situations. Consider as an example the frequentist probability that a person 
contracts a specific disease 
. What should be the population of similar persons in this situation? If we include all men/women of his/her age group we get a large population, but many of the people in this population may not be very “similar” to person 
. We may reduce the population to increase the similarity, but not too much as that would make the population very small and hence inadequate for defining the frequentist probability. This type of dilemma is faced in many types of modeling and a balance has to be made between different concerns: similarity (and hence relevance) vs. population size (and hence validity of the frequentist probability concept, as well as data availability).
, and the fraction of years where scenarios of the different criticality classes occur are denoted 
, 
, 
, and 
. These quantities are unknown, and the standard statistical way to proceed is to establish estimates and describe the associated uncertainty using confidence intervals. A 
confidence interval is defined by
is a parameter and 
and 
random variables. There might be data available to provide an estimate 
of the probability of a cooling system failure event 
; however, for the rarer scenarios, such as the catastrophic one (CA), data directly on the overall event may not be available. A model 
then needs to be introduced which links the conditional frequentist probability of a catastrophic CA scenario (given a cooling system failure event 
), 
, with frequentist probabilities of barrier failures. An event tree may be used for this purpose. Consider for example the following two barriers, illustrated in Figure 2.2:
, the quench system is the first barrier to avoid overheating of the reactor. If the quench system fails, a containment system is intended to mitigate external damage. If both these barriers fail, a catastrophic scenario will occur. The logic of this is illustrated in the event tree of Figure 2.3, where 
denotes failure of the quench system and 
failure of the containment system.
be the vector of barrier failure probabilities, where 
denotes the frequentist probability of quench system failure given a cooling system failure, and 
the frequentist probability of containment system failure given a cooling system failure and quench system failure. From the event tree in Figure 2.3. we construct a model 
of 
by 
. The barrier failure probabilities can be estimated from test data, and an estimate of the probability of a catastrophic failure is obtained as
, an associated confidence interval for this probability can be given. On the other hand, calculating a confidence interval for the unconditional frequentist probability 
is not so straightforward since data directly on the CA scenario is not available.2.3 Subjective Probabilities
The theory of subjective probability was proposed independently and at about the same time by Bruno de Finetti in Fondamenti Logici del Ragionamento Probabilistico (de Finetti, 1930) and Frank Ramsey in The Foundations of Mathematics (Ramsey, 1931); see Gillies (2000).
A subjective probability – sometimes also referred to as a judgmental or knowledge-based probability – is a purely epistemic description of uncertainty as seen by the assigner, based on his or her background knowledge. In this view, the probability of an event 
represents the degree of belief of the assigner with regard to the occurrence of 
. Hence, a probability assignment is a numerical encoding of the state of knowledge of the assessor, rather than a property of the “real world.”
It is important to appreciate that, irrespective of interpretation, any subjective probability is considered to be conditional on the background knowledge 
that the assignment is based on. They are “probabilities in the light of current knowledge” (Lindley, 2006). This can be written as 
, although the writing of 
is normally omitted as the background knowledge is usually unmodified throughout the calculations. Thus, if the background knowledge changes, the probability might also change. Bayes' theorem (see Section 2.4) is the appropriate formal tool for incorporating additional knowledge into a subjective probability. In the context of risk assessment, the background knowledge typically and mainly includes data, models, expert statements, assumptions, and phenomenological understanding.
There are two common interpretations of a subjective probability, one making reference to betting and another to a standard for measurement. The betting interpretation and related interpretations dominate the literature on subjective probabilities, especially within the fields of economy and decision analysis, whereas the standard for measurement is more common among risk and safety analysts.
2.3.1 Betting Interpretation
If derived and interpreted with reference to betting, the probability of an event 
, denoted 
, equals the amount of money that the person assigning the probability would be willing to bet if a single unit of payment were given in return in case event 
were to occur, and nothing otherwise. The opposite must also hold: that is, the assessor must be willing to bet the amount 
if a single unit of payment were given in return in case 
were not to occur, and nothing otherwise. In other words, the probability of an event is the price at which the person assigning the probability is neutral between buying and selling a ticket that is worth one unit of payment if the event occurs and worthless if not (Singpurwalla, 2006). The two-sidedness of the bet is important in order to avoid a so-called Dutch book, that is, a combination of bets (probabilities) that the assigner would be committed to accept but which would lead him or her to a sure loss (Dubucs, 1993). A Dutch book can only be avoided by making so-called coherent bets, meaning bets that can be shown to obey the set of rules that probabilities must obey. In fact, the rules of probability theory can be derived by taking the avoidance of Dutch books as a starting point (Lindley, 2000).
Consider the event 
, defined as the occurrence of a specific type of nuclear accident. Suppose that a person specifies the subjective probability 
. Then, according to the betting interpretation, this person is expressing that he/she is indifferent between:
- receiving (paying) €0.005; and
- taking a gamble in which he/she receives (pays) €1 if
occurs and €0 if 
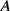does not occur.
If the unit of money is €1000, the interpretation would be that the person is indifferent between:
- receiving (paying) €5; and
- taking a gamble where he/she receives (pays) €1000 if
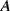occurs and €0 if 
does not occur.
In practice, the probability assignment would be carried out according to an iterative procedure in which different gambles are compared until indifference is reached. However, as noted by Lindley (2006) (see also Cooke, 1986), receiving the payment in the nuclear accident example would be trivial if the accident were to occur (the assessor might not be alive to receive it). The problem is that there is a link between the probability assignment and value judgments about money (the price of the gamble) and the situation (the consequences of the accident). This value judgment has nothing to do with the uncertainties per se, or the degree of belief in the occurrence of event 
.
2.3.2 Reference to a Standard for Uncertainty
A subjective probability can also be understood in relation to a standard for uncertainty, for example, making random withdrawals from an urn. If a person assigns a probability of 0.1 (say) to an event 
, then this person compares his/her uncertainty (degree of belief) in the occurrence of 
to drawing a specific ball from an urn containing 10 balls. The uncertainty (degree of belief) is the same. More generally, the probability 
is the number such that the uncertainty about the occurrence of 
is considered equivalent, by the person assigning the probability, to the uncertainty about the occurrence of some standard event, for example, drawing, at random, a red ball from an urn that contains 
red balls (see, e.g., Lindley, 2000, 2006; Bernardo and Smith, 1994).
linking the occurrence of a cooling system failure (D) with the occurrence of a catastrophic scenario (CA) through the barrier failure events 
. Here 
is the indicator function equal to 1 if the argument is true and 0 otherwise. Then, we obtain
is the expected value operator.As for the betting interpretation, the interpretation with reference to an uncertainty standard can be used to deduce the rules of probability; see Lindley (2000). These rules are typically referred to as axioms in textbooks on probability, but they are not axioms here, since they are deduced from more basic assumptions linked to the uncertainty standard; see Lindley (2000, p. 299). Whether the probability rules are deduced or taken as axioms may not be so important to applied probabilists. The main point is that these rules apply, and the uncertainty standard provides an easily understandable way of defining and interpreting subjective probability where uncertainty/probability and utility/value are separated. The rules of probability reduce to the rules governing proportions, which are easy to communicate.
2.4 The Bayesian Subjective Probability Framework
The so-called Bayesian framework has subjective probability as a basic component, and the term “probability” is reserved for, and always understood as, a degree of belief. Within this framework, the term “chance” is used by some authors (e.g., Lindley, 2006; Singpurwalla, 2006; Singpurwalla and Wilson, 2008) for the limit of a relative frequency in an exchangeable, infinite Bernoulli series. A chance distribution is the limit of an empirical distribution function (Lindley, 2006). Two random quantities 
and 
are said to be exchangeable if for all values 
and 
that 
and 
may take, we have
(2.5) 
That is, the probabilities remain unchanged (invariant) when switching (permuting) the indices. The relationship between subjective probability and the chance concept is given by the so-called representation theorem of de Finetti; see, for example, Bernardo and Smith (1994, p. 172). Roughly speaking, this theorem states that if an exchangeable Bernoulli series can be introduced, one may act as though frequency probabilities exist.
In the case when a chance 
of an event 
may be introduced, we have 
. That is, the probability of an event 
for which the associated chance is known is simply equal to the value of the chance. For unknown 
, observations of outcomes in similar (exchangeable) situations would not be considered independent of the situation of interest, since the observations would provide more information about the value of 
. On the other hand, for known 
the outcomes would be judged as independent, since nothing more could be learned about 
from additional observations. Hence, conditional on 
, the outcomes are independent, but unconditionally they are not – they are exchangeable. In practice, the value of a chance 
is in most cases unknown and the assessor expresses his or her uncertainty about the value of 
by a probability distribution 
. As in the example of Section 1.1.3, the probability of 
can then be derived as
The probability 
in this equation characterizes uncertainty about the occurrence of event A, given the background knowledge 
(suppressed from the notation), which includes a judgment of exchangeability which allows for the equivalence relation 
, as well as the information contained in 
. Consequently, the uncertainty about p does not make 
uncertain.
More generally, if a chance distribution is known, then under judgment of exchangeability the probability distribution is equal to the chance distribution, which is analogous to setting 
. If the chance distribution is unknown, a “prior” probability distribution is established over the chance distribution (parameters), updated to a “posterior” distribution upon receiving new information, and the “predictive” probability distribution may be established by using the law of total probability, as illustrated in (2.6). The updating is performed using Bayes' rule, which states that
(2.7) 
for 
.
denote the chance of a catastrophic (CA) scenario; also let 
denote the chance of a cooling system failure (chance of event D), 
the chance of a quenching system failure (chance of event 
), and 
the chance of a containment system failure (chance of event 
). Then we have a chance model 
as follows:
.
. Analogously to (2.6), the probability of the catastrophic scenario is given as
may be derived, describing the degree of uncertainty on the value of the chance of a CA scenario. From this probability distribution a credibility interval may then be derived, say a 90% credibility interval 
specifying that with a 90% probability the actual value of 
is in the interval 
, where 
and 
are fixed quantities.2.5 Logical Probabilities
Logical probabilities were first proposed by Keynes (1921) and later taken up by Carnap (1922, 1929). The idea is that probability expresses an objective logical relation between propositions – a sort of “partial entailment.” There is a number in the interval 
, denoted 
, which measures the objective degree of logical support that evidence E gives to hypothesis 
(Franklin, 2001). As stated by Franklin (2001), this view on probability has an intuitive initial attractiveness in representing a level of agreement found when scientists, juries, actuaries, and so on evaluate hypotheses in the light of evidence. However, as described by Aven (2013a), the notion of partial entailment has never received a satisfactory interpretation, and also both Cowell et al. (1999) and Cooke (2004) conclude that this interpretation of probability cannot be justified.