Having taught assembly language programming for many years, I’ve discovered that most people don’t understand the fundamental difference between a number and the representation of that number. Most of the time this confusion is harmless. However, many algorithms depend upon the internal and external representations we use for numbers to operate correctly and efficiently. If you do not understand the difference between the abstract concept of a number and the representation of that number, you’ll have trouble understanding, using, or creating such algorithms. Fully understanding this difference could take you from creating some mediocre code to creating great code.

A number is an intangible, abstract, concept. It is an intellectual device that we use to denote quantity. Let’s say I were to tell you that “some book has one hundred pages.” You could touch the pages — they are tangible. You could even count those pages to verify that there are one hundred of them. However, “one hundred” is simply an abstraction that I would be applying to the book as a way of describing its size.

The important thing to realize is that the following is not one hundred:

This is nothing more than ink on paper forming certain lines and curves. You might recognize this sequence of symbols as a representation of one hundred, but this is not the actual value 100. It’s just three symbols appearing on this page. It isn’t even the only representation for one hundred — consider the following, which are all different representations of the value one hundred:

The representation of a number is (generally) some sequence of symbols. For example, the common representation of the value one hundred, “100,” is really a sequence of three numeric digits: the digit 1 followed by the digit 0 followed by a second 0 digit. Each of these digits has some specific meaning, but we could have just as easily used the sequence “64” to represent the value one hundred. Even the individual digits that comprise this representation of 100 are not numbers. They are numeric digits, tools we use to represent numbers, but they are not numbers themselves.

Now you may be wondering why we should even care whether a sequence of symbols like “100” is the actual value one hundred or just the representation of this value. The reason for this distinction is that you’ll encounter several different sequences of symbols in a computer program that look like numbers (meaning that they look like “100”), and you don’t want to confuse them with actual numeric values. Conversely, there are many different representations for the value one hundred that a computer could use, and it’s important for you to realize that they are equivalent.

A numbering system is a mechanism we use to represent numeric values. In today’s society, people most often use the decimal numbering system (base 10) and most computer systems use binary representation. Confusion between the two can lead to poor coding practices. So to write great code, you must eliminate this confusion.

To appreciate the difference between numbers and their representations, let’s start with a concrete discussion of the decimal numbering system. The Arabs developed the decimal numbering system we commonly use today (indeed, the ten decimal digits are known as Arabic numerals). The Arabic system uses a positional notation system to represent values with a relatively small number of different symbols. That is, the Arabic representation takes into consideration not only the symbol itself, but the position of the symbol in a sequence of symbols, a scheme that is far superior to other, nonpositional, representations. To appreciate the difference between a positional system and a nonpositional system, consider the tally-slash representation of the number 25 in Figure 2-1.

Figure 2-1. Tally-slash representation of 25

The tally-slash representation uses a sequence of n marks to represent the value n. To make the values easier to read, most people arrange the tally marks in groups of five, as in Figure 2-1. The advantage of the tally-slash numbering system is that it is easy to use when counting objects. The disadvantages include the fact that the notation is bulky, and arithmetic operations are difficult. However, without question, the biggest problem with the tally-slash representation is the amount of physical space this representation consumes. To represent the value n requires some amount of space that is proportional to n. Therefore, for large values of n, the tally-slash notation becomes unusable.

2.2.1 The Decimal Positional Numbering System

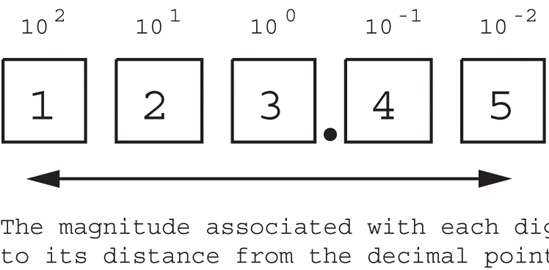
The decimal positional notation (base 10) represents numbers using strings of Arabic numerals. The symbol immediately to the left of the decimal point in the sequence represents some value between zero and nine. If there are at least two digits, then the second symbol to the left of the decimal point represents some value between zero and nine times ten. In the decimal positional numbering system each digit appearing to the left of the decimal point represents a value between zero and nine times an increasing power of ten (see Figure 2-2).

Figure 2-2. A positional numbering system

When you see a numeric sequence like “123.45,” you don’t think about the value 123.45; rather, you generate a mental image of this quantity. In reality, 123.45 represents:

1 × 102 + 2 × 101 + 3 × 100 + 4 × 10−1 + 5 × 10−2

or

100 + 20 + 3 + 0.4 + 0.05

To get a clear picture of how powerful this notation is, consider the following facts:

• The positional numbering system, using base 10, can represent the value ten in one-third the space of the tally-slash system.

• The base-10 positional numbering system can represent the value one hundred in about 3 percent of the space of the tally-slash system.

• The base-10 positional numbering system can represent the value one thousand in about 0.3 percent of the space of the tally-slash system.

As the numbers grow larger, the disparity becomes even greater. Because of the compact and easy-to-recognize notation, positional numbering systems are quite popular.

1 × 82 + 2 × 81 + 3 × 80

64 + 16 + 3

1 × 27 + 1 × 26 + 0 × 25 + 0 × 24 + 1 × 23 + 0 × 22 + 1 × 21 + 0 × 20

128 + 64 + 8 + 2

20210

%11_1011_0010_1101

1 × 163 + 2 × 162 + 3 × 161 + 4 × 160

4096 + 512 + 48 + 4

466010

23416 DEAD16 BEEF16 0AFB16 FEED16 DEAF16

1   2   3
001 010 011

Because most programming languages (or their libraries) provide automatic numeric/string conversions, beginning programmers are often unaware that this conversion is even taking place. In this section we’ll consider two conversions: from string to numeric form and from numeric form to string.

Consider how easy it is to convert a string to numeric form in various languages. In each of the following statements, the variable i can hold some integer number. The input from the user’s console, however, is a string of characters. The programming language’s run-time library is responsible for converting that string of characters to the internal binary form the CPU requires.

cin >> i;     // C++
readln( i );  // Pascal
input i       // BASIC
stdin.get(i); // HLA

Because these statements are so easy to use, most programmers don’t consider the cost of using such statements in their programs. Unfortunately, if you have no idea of the cost of these statements, you’ll not realize how they can impact your program when performance is critical. The reason for exploring these conversion algorithms here is to make you aware of the work involved so you will not make frivolous use of these conversions.

To simplify things, we’ll discuss unsigned integer values and ignore the possibility of illegal characters and numeric overflow. Therefore, the following algorithms actually understate the actual work involved (by a small amount).

Use this algorithm to convert a string of decimal digits to an integer value:

Converting an integer value to a string of characters takes even more effort. The algorithm for the conversion is the following:

The particulars of these algorithms are not important. What is important to note is that these steps execute once for each output character and division is very slow. So a simple statement like one of the following can hide a fair amount of work from the programmer:

printf( "%d", i );    // C
cout << i;            // C++
print i               // BASIC
write( i );           // Pascal
stdout.put( i );      // HLA

To write great code you don’t need to eschew the use of numeric/string conversions. They are an important part of computation, and great code will need to do these conversions. However, a great programmer will be careful about the use of numeric/string conversions and only use them as necessary.

Note that these algorithms are only valid for unsigned integers. Signed integers require a little more effort to process (though the extra work is almost negligible). Floating-point values, however, are far more difficult to convert between string and numeric form. That’s something to keep in mind when writing code that uses floating-point arithmetic.

Most modern computer systems are binary computer systems and, therefore, use an internal binary format to represent values and other objects. However, most systems cannot represent just any binary value. Instead, they are only capable of efficiently representing binary values of a given size. If you want to write great code, you need to make sure that your programs use data objects that the machine can represent efficiently. The following sections describe how computers physically represent values.

2.4.2 Bit Strings

As you’ve already seen in this chapter, by combining bits into a sequence, we can form binary representations that are equivalent to other representations of numbers (like hexadecimal and octal). Most computer systems, however, do not let you collect together an arbitrary number of bits. Instead, you have to work with strings of bits that have certain fixed lengths. In this section we’ll discuss some of the more common bit string lengths and the names computer engineers have given them.

A nibble is a collection of four bits. Most computer systems do not provide efficient access to nibbles in memory. However, nibbles are interesting to us because it takes exactly one nibble to represent a single hexadecimal digit.

A byte is eight bits and it is the smallest addressable data item on many CPUs. That is, the CPU can efficiently retrieve data on an 8-bit boundary from memory. For this reason, the smallest data type that many languages support consumes one byte of memory (regardless of the actual number of bits the data type requires).

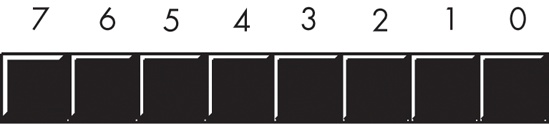
Because the byte is the smallest unit of storage on most machines, and many languages use bytes to represent objects that require fewer than eight bits, we need some way of denoting individual bits within a byte. To describe the bits within a byte, we’ll use bit numbers. Normally, we’ll number the bits in a byte, as Figure 2-3 shows. Bit 0 is the low-order (LO) bit or least significant bit, and bit 7 is the high-order (HO) bit or most significant bit of the byte. We’ll refer to all other bits by their number.

Figure 2-3. Bit numbering in a byte

The term word has a different meaning depending on the CPU. On some CPUs a word is a 16-bit object. On others a word is a 32-bit or 64-bit object. In this text, we’ll adopt the 80x86 terminology and define a word to be a 16-bit quantity. Like bytes, we’ll number the bits in a word starting with bit number zero for the LO bit and work our way up to the HO bit (bit 15), as in Figure 2-4. When referencing the other bits in a word, use their bit position number.

Figure 2-4. Bit numbers in a word

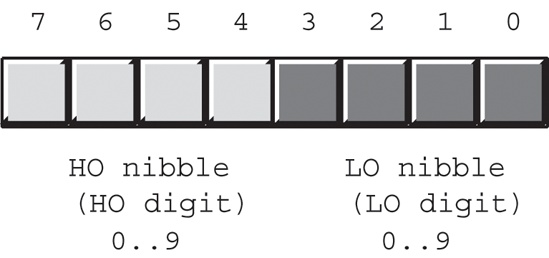
Notice that a word contains exactly two bytes. Bits 0 through 7 form the LO byte, bits 8 through 15 form the HO byte (see Figure 2-5).

Figure 2-5. The two bytes in a word

A double word is exactly what its name implies, a pair of words (sometimes you will see “double word” abbreviated as “dword”). Therefore, a double-word quantity is 32 bits long, as shown in Figure 2-6.

Figure 2-6. Bit layout in a double word

A double word contains a pair of words and a set of four bytes, as Figure 2-7 shows.

Figure 2-7. Bytes and words in a double word

Most CPUs efficiently handle objects up to a certain size (typically 32 or 64 bits on contemporary systems). That does not mean you can’t work with larger objects — it simply becomes less efficient to do so. For that reason, you typically won’t see programs handling numeric objects much larger than about 128 or 256 bits. Because 64-bit integers are available in some programming languages, and most languages support 64-bit floating-point values, it does make sense to describe a 64-bit data type; we’ll call these quad words. Just for the fun of it, we’ll use the term long word for 128-bit values. Few languages today support 128 bit values,^[2] but this does give us some room to grow.

Of course, we can break quad words down into 2 double words, 4 words, 8 bytes, or 16 nibbles. Likewise, we can break long words down into 2 quad words, 4 double words, 8 words, or 16 bytes.

On Intel 80x86 platforms there is also an 80-bit type that Intel calls a tbyte (for 10-byte) object. The 80x86 CPU family uses tbyte variables to hold extended precision floating-point values and certain binary-coded decimal (BCD) values.

In general, with an n-bit string you can represent up to 2ⁿ different values. Table 2-3 shows the number of possible objects you can represent with nibbles, bytes, words, double words, quad words, and long words.

Table 2-3. Number of Values Representable with Bit Strings

Size of Bit String (in Bits)	Number of Possible Combinations (2n)
4	16
8	256
16	65,536
32	4,294,967,296
64	18,446,744,073,709,551,616
128	340,282,366,920,938,463,463,374,607,431,768,211,456

The binary number 0...00000^[3] represents zero, 0...00001 represents one, 0...00010 represents two, and so on towards infinity. But what about negative numbers? To represent signed values, most computer systems use the two’s complement numbering system. The representation of signed numbers places some fundamental restrictions on those numbers, so it is important to understand the difference in representation between signed and unsigned numbers in a computer system to use them efficiently.

With n bits we can only represent 2ⁿ different objects. As negative values are objects in their own right, we’ll have to divide these 2ⁿ combinations between negative and non-negative values. So, for example, a byte can represent the negative values −128..−1 and the non-negative values 0..127. With a 16-bit word we can represent signed values in the range −32,768..+32,767. With a 32-bit double word we can represent values in the range −2,147,483,648..+2,147,483,647. In general, with n bits we can represent the signed values in the range −2ⁿ⁻¹ to +2ⁿ⁻¹−1.

The two’s complement system uses the HO bit as a sign bit. If the HO bit is zero, the number is non-negative; if the HO bit is one, the number is negative. Here are some examples using 16-bit numbers:

$8000 (%1000_0000_0000_0000) is negative because the HO bit is one
$100 (%0000_0001_0000_0000) is non-negative because the HO bit is zero
$7FFF (%0111_1111_1111_1111) is non-negative
$FFFF (%1111_1111_1111_1111) is negative
$FFF (%0000_1111_1111_1111) is non-negative

To negate a two’s complement number, you can use the following algorithm:

For example, these are the steps to compute the 8-bit equivalent of the decimal value −5:

%0000_0101        Five (in binary)
%1111_1010        Invert all the bits
%1111_1011        Add one to obtain −5 (in two's complement form)

If we take −5 and negate it, the result is 5 (%0000_0101), just as we expect:

%1111_1011        Two's complement for −5
%0000_0100        Invert all the bits
%0000_0101        Add one to obtain 5 (in binary)

Here are some 16-bit examples and their negations:

First, negate 32,767 ($7fff):

$7FFF:   %0111_1111_1111_1111    +32,767, the largest 16-bit positive number.
         %1000_0000_0000_0000    Invert all the bits (8000h)
         %1000_0000_0000_0001    Add one (8001h or −32,767)

First, negate 16,384 ($4000):

$4000:   %0100_0000_0000_0000    16,384
         %1011_1111_1111_1111    Invert all the bits ($BFFF)
         %1100_0000_0000_0000    Add one ($C000 or −16,384)

And now negate −32,768 ($8000):

$8000:   %1000_0000_0000_0000    −32,768, the smallest 16-bit negative number.
         %0111_1111_1111_1111    Invert all the bits ($7FFF)
         %1000_0000_0000_0000    Add one ($8000 or −32768)

$8000 inverted becomes $7FFF, and after adding one we obtain $8000! Wait, what’s going on here? −(−32,768) is −32,768? Of course not. However, the 16-bit two’s complement numbering system cannot represent the value +32,768. In general, you cannot negate the smallest negative value in the two’s complement numbering system.

It’s worth learning a few interesting facts about binary values that you might find useful in your programs. Here are some useful properties:

You should probably memorize all the powers of two from 2⁰ through 2¹⁶, as these values come up in programs all the time. Table 2-4 lists their values.

Many modern high-level programming languages allow you to use expressions involving integer objects with differing sizes. So what happens when your two operands in an expression are of different sizes? Some languages will report an error, other languages will automatically convert the operands to a common format. This conversion, however, is not free, so if you don’t want your compiler going behind your back and automatically inserting conversions into your otherwise great code, you should be aware of how compilers deal with such expressions.

With the two’s complement system, a single negative value will have different representations depending on size of the representation. You cannot arbitrarily use an 8-bit signed value in an expression involving a 16-bit number; a conversion will be necessary. This conversion, and its converse (converting a 16-bit value to 8 bits) are the sign extension and contraction operations.

Consider the value −64. The 8-bit two’s complement value for this number is $C0. The 16-bit equivalent of this number is $FFC0. Clearly, these are not the same bit pattern. Now consider the value +64. The 8- and 16-bit versions of this value are $40 and $0040, respectively. It should be obvious that extending the size of negative values is done differently than extending the size of non-negative values.

To sign extend a value from some number of bits to a greater number of bits is easy — just copy the sign bit into the additional HO bits in the new format. For example, to sign extend an 8-bit number to a 16-bit number, simply copy bit seven of the 8-bit number into bits 8..15 of the 16-bit number. To sign extend a 16-bit number to a double word, simply copy bit 15 into bits 16..31 of the double word.

You must use sign extension when manipulating signed values of varying lengths. For example, when adding a byte quantity to a word quantity, you will need to sign extend the byte to 16 bits before adding the two numbers. Other operations may require a sign extension to 32 bits.

When processing unsigned binary numbers, zero extension lets you convert small unsigned values to larger unsigned values. Zero extension is very easy — just store a zero in the HO byte(s) of the larger operand. For example, to zero extend the 8-bit value $82 to 16 bits you just insert a zero for the HO byte yielding $0082.

Many high-level language compilers automatically handle sign and zero extension. The following examples in C demonstrate how this works:

signed char sbyte;    // Chars in C are byte values.
short int sword;      // Short integers in C are *usually* 16-bit values.
long int sdword;      // Long integers in C are *usually* 32-bit values.
 . . .
sword = sbyte;   // Automatically sign extends the 8-bit value to 16 bits.
sdword = sbyte;  // Automatically sign extends the 8-bit value to 32 bits.
sdword = sword;  // Automatically sign extends the 16-bit value to 32 bits.

Some languages (such as Ada) may require an explicit cast from a smaller size to a larger size. You’ll have to check the language reference manual for your particular language to see if this is necessary. The advantage of a language that requires you to provide an explicit conversion is that the compiler never does anything behind your back. If you fail to provide the conversion yourself, the compiler emits a diagnostic message so you’ll be made aware that your program will need to do additional work.

The important thing to realize about sign and zero extension is that they aren’t always free. Assigning a smaller integer to a larger integer may require more machine instructions (taking longer to execute) than moving data between two like-sized integer variables. Therefore, you should be careful about mixing variables of different sizes within the same arithmetic expression or assignment statement.

Sign contraction, converting a value with some number of bits to the same value with a fewer number of bits, is a little more troublesome. Sign extension never fails. Given an m-bit signed value you can always convert it to an n-bit number (where n > m) using sign extension. Unfortunately, given an n-bit number, you cannot always convert it to an m-bit number if m < n. For example, consider the value −448. As a 16-bit hexadecimal number, its representation is $FE40. Unfortunately, the magnitude of this number is too large to fit into eight bits, so you cannot sign contract it to eight bits.

To properly sign contract one value to another, you must look at the HO byte(s) that you want to discard. First, the HO bytes must all contain either zero or $FF. If you encounter any other values, you cannot sign contract the value. Second, the HO bit of your resulting value must match every bit you’ve removed from the number. Here are some examples of converting 16-bit values to 8-bit values:

$FF80 (%1111_1111_1000_0000) can be sign contracted to $80 (%1000_0000).
$0040 (%0000_0000_0100_0000) can be sign contracted to $40 (%0100_0000).
$FE40 (%1111_1110_0100_0000) cannot be sign contracted to 8 bits.
$0100 (%0000_0001_0000_0000) cannot be sign contracted to 8 bits.

Contraction is somewhat difficult in a high-level language. Some languages, like C, will simply store the LO portion of the expression into a smaller variable and throw away the HO component (at best, the C compiler may give you a warning during compilation about the loss of precision that may occur). You can often quiet the compiler, but it still doesn’t check for invalid values. Typically, you’d use code like the following to sign contract a value in C:

signed char sbyte;    // Chars in C are byte values.
short int sword;      // Short integers in C are *usually* 16-bit values.
long int sdword;      // Long integers in C are *usually* 32-bit values.
 . . .
sbyte = (signed char) sword;
sbyte = (signed char) sdword;
sword = (short int) sdword;

The only safe solution in C is to compare the result of the expression to an upper and lower bounds value before attempting to store the value into a smaller variable. Unfortunately, such code tends to get unwieldy if you need to do this often. Here’s what the preceding code might look like with these checks:

if( sword >= −128 && sword <= 127 )
{
    sbyte = (signed char) sword;
}
else
{
    // Report appropriate error.
}

// Another way, using assertions:

assert( sdword >= −128 && sdword <= 127 )
sbyte = (signed char) sword;

assert( sdword >= −32768 && sdword <= 32767 )
sword = (short int) sword;

As you can plainly see, this code gets pretty ugly. In C/C++, you’d probably want to turn this into a macro (#define) or a function so your code would be a bit more readable.

Some high-level languages (such as Pascal and Delphi/Kylix) will automatically sign contract values for you and check the value to ensure it properly fits in the destination operation.^[4] Such languages will raise some sort of exception (or stop the program) if a range violation occurs. Of course, if you want to take corrective action, you’ll either need to write some exception handling code or resort to using an if statement sequence similar to the one in the C example just given.

Saturation is another way to reduce the size of an integer value. Saturation is useful when you want to convert a larger object to a smaller object and you’re willing to live with possible loss of precision. If the value of the larger object is not outside the range of the smaller object, you can convert the value via saturation by copying the LO bits of the larger value into the smaller object. If the larger value is outside the smaller object’s range, then you clip the larger value by setting it to the largest (or smallest) value within the range of the smaller data type.

When converting a 16-bit signed integer to an 8-bit signed integer, if the 16-bit value is in the range −128..+127 you simply copy the LO byte into the 8-bit object. If the 16-bit signed value is greater than +127, then you clip the value to +127 and store +127 into the 8-bit object. Likewise, if the value is less than −128, you clip the final 8-bit object to −128. Saturation works the same way when clipping 32-bit values to smaller values. If the larger value is outside the range of the smaller value, then you simply clip the value to the closest value that you can represent with the smaller data type.

If the larger value is outside the range of the smaller value, there will be a loss of precision during the conversion. While clipping the value is never desirable, sometimes this is better than raising an exception or otherwise rejecting the calculation. For many applications, such as audio or video, the clipped result is still recognizable to the end user, so this is a reasonable conversion scheme in such situations.

As a result, many CPUs support saturation arithmetic in their special “multimedia extension” instruction sets. On the Intel 80x86 processor family, for example, the MMX instruction extensions provide saturation capabilities. Most CPUs’ standard instruction sets, as well as most high-level languages, do not provide direct support for saturation, but saturation is not difficult. Consider the following Pascal/Delphi/Kylix code that uses saturation to convert a 32-bit integer to a 16-bit integer:

var
    li  :longint;
    si  :smallint;
        . . .
    if( li > 32767 ) then

        si := 32767;

    else if( li < −32768 ) then

        si := −32768;

    else
        si := li;

The binary-coded decimal (BCD) format, as its name suggests, encodes decimal values using a binary representation. The 80x86 CPU family provides several machine instructions that convert between BCD and pure binary formats. Common general-purpose high-level languages (like C/C++, Pascal, and Java) rarely support decimal values. However, business-oriented programming languages (like COBOL and many database languages) support this data type. So if you’re writing code that interfaces with a database or some language that supports decimal arithmetic, you may need to deal with BCD representation.

BCD values consist of a sequence of nibbles, with each nibble representing a value in the range 0..9. Of course, you can represent values in the range 0..15 using a nibble; the BCD format, however, uses only 10 of the possible 16 values. Each nibble represents a single decimal digit in a BCD value, so with a single byte we can represent values containing two decimal digits (0..99), as shown in Figure 2-8. With a word, we can represent values having four decimal digits (0..9999). Likewise, a double word can represent up to eight decimal digits.

Figure 2-8. BCD data representation in a byte

As you can see, BCD storage isn’t particularly efficient. An 8-bit BCD variable can represent values in the range 0..99 while that same eight bits, holding a binary value, could represent values in the range 0..255. Likewise, a 16-bit binary value can represent values in the range 0..65535 while a 16-bit BCD value can only represent about a sixth of those values (0..9999). Inefficient storage isn’t the only problem with BCD, though. BCD calculations also tend to be slower than binary calculations.

At this point, you’re probably wondering why anyone would ever use the BCD format. The BCD format does have two saving graces: it’s very easy to convert BCD values between the internal numeric representation and their decimal string representations, and it’s also very easy to encode multidigit decimal values in hardware when using BCD — for example, when using a set of dials with each dial representing a single digit. For these reasons, you’re likely to see people using BCD in embedded systems (such as toaster ovens and alarm clocks) but rarely in general-purpose computer software.

A few decades ago people mistakenly thought that calculations involving BCD (or just decimal) arithmetic were more accurate than binary calculations. Therefore, they would often perform important calculations, like those involving dollars and cents (or other monetary units) using decimal-based arithmetic. While it is true that certain calculations can produce more accurate results in BCD, this statement is not true in general. Indeed, for most calculations the binary representation is more accurate. For this reason, most modern computer programs represent all values (including decimal values) in a binary form. For example, the Intel 80x86 floating-point unit (FPU) supports a pair of instructions for loading and storing BCD values. Internally, however, the FPU converts these BCD values to binary. It only uses BCD as an external data format (external to the FPU, that is). This generally produces more accurate results.

One thing you may have noticed by now is that this discussion has dealt mainly with integer values. A reasonable question to ask is how one represents fractional values. There are two ways computer systems commonly represent numbers with fractional components: fixed-point representation and floating-point representation.

Back in the days when CPUs didn’t support floating-point arithmetic in hardware, fixed-point arithmetic was very popular with programmers writing high-performance software that dealt with fractional values. The software overhead necessary to support fractional values in a fixed-point format is less than that needed to do the same calculation using a software-based floating-point computation. However, as the CPU manufacturers added floating-point units (FPUs) to their CPUs to support floating-point in hardware, the advantages of fixed-point arithmetic waned considerably. Today, it’s fairly rare to see someone attempt fixed-point arithmetic on a general-purpose CPU that supports floating-point arithmetic. It’s usually more cost effective to use the CPU’s native floating-point format.

Although CPU manufacturers have worked hard at optimizing the floating-point arithmetic on their systems, reducing the advantages of fixed-point arithmetic, carefully written assembly language programs can make effective use of fixed-point calculations in certain circumstances and the code will run faster than the equivalent floating-point code. Certain 3D gaming applications, for example, may produce faster computations using a 16:16 (16-bit integer, 16-bit fractional) format rather than a 32-bit floating-point format. Because there are some very good uses for fixed-point arithmetic, this section discusses fixed-point representation and fractional values using the fixed-point format (Chapter 4 will discuss the floating-point format).

Fractional values fall between zero and one, and positional numbering systems represent fractional values by placing digits to the right of the radix point. In the binary numbering system, each bit to the right of the binary point represents the value zero or one multiplied by some successive negative power of two. Therefore, when representing values with a fractional component in binary, we represent that fractional component using sums of binary fractions. For example, to represent the value 5.25 in binary, we would use the following binary value:

101.01

The conversion to decimal yields:

1 × 22 + 1 × 20 + 1 × 2−2 = 4 + 1 + 0.25 = 5.25

When using a fixed-point binary format you choose a particular bit in the binary representation and implicitly place the binary point before that bit. For a 32-bit fixed-point format you could place the binary point before (or after) any of the 32 bits. You choose the position of the binary point based on the number of significant bits you require in the fractional portion of the number. For example, if your values’ integer components can range from 0 to 999, you’ll need at least 10 bits to the left of the binary point to represent this range of values. If you require signed values, you’ll need an extra bit for the sign. In a 32-bit fixed-point format, this leaves either 21 or 22 bits for the fractional part, depending on whether your value is signed.

Fixed-point numbers are a small subset of the real numbers. Because there are an infinite number of values between any two integer values, fixed-point values cannot exactly represent every value between two integers (doing so would require an infinite number of bits). With fixed-point representation, we have to approximate most of the real numbers. Consider the 8-bit fixed-point format that uses six bits for the integer portion and two bits for the fractional component. The integer component can represent values in the range 0..63 (or any other 64 values, including signed values in the range −32..+31). The fractional component can only represent four different values, typically 0.0, 0.25, 0.5, and 0.75. You cannot exactly represent 1.3 with this format; the best you can do is approximate 1.3 by choosing the value closest to 1.3 (which is 1.25). Obviously, this introduces error. You can reduce this error by adding additional bits to the right of the binary point in your fixed-point format (at the expense of reducing the range of the integer component or adding additional bits to your fixed-point format). For example, if you move to a 16-bit fixed-point format using an 8-bit integer and an 8-bit fractional component, then you can approximate 1.3 using the following binary value:

1.01001101

The decimal equivalent is as follows:

1 + 0.25 + 0.03125 + 0.15625 + 0.00390625 = 1.30078125

As you can see, adding more bits to the fractional component of your fixed-point number will give you a more accurate approximation of this value (the error is only 0.00078125 using this format compared to 0.05 in the previous format).

However, when using a fixed-point binary numbering system, there are certain values you can never accurately represent regardless of how many bits you add to the fractional part of your fixed-point representation (1.3 just happens to be such a value). This is probably the main reason why people (mistakenly) feel that decimal arithmetic is more accurate than binary arithmetic (particularly when working with decimal fractions like 0.1, 0.2, 0.3, and so on).

To contrast the comparative accuracy of the two systems, let’s consider a fixed-point decimal system (using BCD representation). If we choose a 16-bit format with eight bits for the integer portion and eight bits for the fractional portion, we can represent decimal values in the range 0.0 to 99.99 with two decimal digits of precision to the right of the decimal point. We can exactly represent values like 1.3 in this BCD notation using a hex value like $0130 (the implicit decimal point appears between the second and third digits in this number). As long as you only use the fractional values 0.00..0.99 in your computations, this BCD representation is, indeed, more accurate than the binary fixed-point representation (using an 8-bit fractional component). In general, however, the binary format is more accurate.

The binary format lets you exactly represent 256 different fractional values, whereas the BCD format only lets you represent 100 different fractional values. If you pick an arbitrary fractional value, it’s likely the binary fixed-point representation provides a better approximation than the decimal format (because there are over two and a half times as many binary versus decimal fractional values). The only time the decimal fixed-point format has an advantage is when you commonly work with the fractional values that it can exactly represent. In the United States, monetary computations commonly produce these fractional values, so programmers figured the decimal format is better for monetary computations. However, given the accuracy most financial computations require (generally four digits to the right of the decimal point is the minimum precision serious financial transactions require), it’s usually better to use a binary format.

For example, with a 16-bit fractional component, the decimal/BCD fixed-point format gives you exactly four digits of precision; the binary format, on the other hand, offers over six times the resolution (65,536 different fractional values rather than 10,000 fractional values). Although the binary format cannot exactly represent some of the values that you can exactly represent in decimal form, the binary format does exactly represent better than six times as many values. Once you round the result down to cents (two digits to the right of the decimal point), you’re definitely going to get better results using the binary format.

If you absolutely, positively, need to exactly represent the fractional values between 0.00 and 0.99 with at least two digits of precision, the binary fixed-point format is not a viable solution. Fortunately, you don’t have to use a decimal format; there are other binary formats that will let you exactly represent these values. The next couple of sections describe such formats.

Because the decimal (BCD) formats can exactly represent some important values that you cannot exactly represent in binary, many programmers have chosen to use decimal arithmetic in their programs despite the better precision and performance of the binary format. However, there is a better numeric representation that offers the advantages of both schemes: the exact representation of certain decimal fractions combined with the precision of the binary format. This numeric format is also efficient to use and doesn’t require any special hardware. What’s this wonderful format? It’s the scaled numeric format.

One advantage of the scaled numeric format is that you can choose any base, not just decimal, for your format. For example, if you’re working with ternary (base-3) fractions, you can multiply your original input value by three (or some power of three) and exactly represent values like ¹/₃, ²/₃, ⁴/₉, ⁷/₂₇, and so on. You cannot exactly represent any of these values in either the binary or decimal numbering systems.

The scaled numeric format uses fast, compact integer arithmetic. To represent fractional values, you simply multiply your original value by some value that converts the fractional component to a whole number. For example, if you want to maintain two decimal digits of precision to the right of the decimal point, simply multiply your values by 100 upon input. This translates values like 1.3 to 130, which we can exactly represent using an integer value. Assuming you do this calculation with all your fractional values (and they have the same two digits of precision to the right of the decimal point), you can manipulate your values using standard integer arithmetic operations. For example, if you have the values 1.5 and 1.3, their integer conversion produces 150 and 130. If you add these two values you get 280 (which corresponds to 2.8). When you need to output these values, you simply divide them by 100 and emit the quotient as the integer portion of the value and the remainder (zero extended to two digits, if necessary) as the fractional component. Other than the need to write specialized input and output routines that handle the multiplication and division by 100 (as well as dealing with the decimal point), this scaled numeric scheme is almost as easy as doing regular integer calculations.

Of course, do keep in mind that if you scale your values as described here, you’ve limited the maximum range of the integer portion of your numbers by a like amount. For example, if you need two decimal digits of precision to the right of your decimal point (meaning you multiply the original value by 100), then you may only represent (unsigned) values in the range 0..42,949,672 rather than the normal range of 0..4,294,967,296.

When doing addition or subtraction with a scaled format, you must ensure that both operands have the same scaling factor. That is, if you’ve multiplied the left operand of an addition operator by 100, you must have multiplied the right operand by 100 as well. Ditto for subtraction. For example, if you’ve scaled the variable i10 by ten and you’ve scaled the variable j100 by 100, you need to either multiply i10 by ten (to scale it by 100) or divide j100 by ten (to scale it down to ten) before attempting to add or subtract these two numbers. When using the addition and subtraction operators, you ensure that both operands have the radix point in the same position (and note that this applies to literal constants as well as variables).

When using the multiplication and division operators, the operands do not require the same scaling factor prior to the operation. However, once the operation is complete, you may need to adjust the result. Suppose you have two values you’ve scaled by 100 to produce two digits of precision after the decimal point and those values are i = 25 (0.25) and j = 1 (0.01). If you compute k = i * j using standard integer arithmetic, the result you’ll get is 25 (25 × 1 = 25). Note that the actual value should be 0.0025, yet the result appearing in i seems to be 0.25. The computation is actually correct; the problem is understanding how the multiplication operator works. Consider what we’re actually computing:

(0.25 × (100)) × (0.01 × (100))
                              =
0.25 × 0.01 × (100 × 100)    // commutative laws allow this
                              =
                      0.0025 × (10,000)
                              =
                             25

The problem is that the final result actually gets scaled by 10,000. This is because both i and j have been multiplied by 100 and when you multiply their values, you wind up with a value multiplied by 10,000 (100 × 100) rather than 100. To solve this problem, you should divide the result by the scaling factor once the computation is complete. For example, k = i * j/100.

The division operation suffers from a similar (though not the exact same) problem. Suppose we have the values m = 500 (5.0) and n = 250 (2.5) and we want to compute k = m/n. We would normally expect to get the result 200 (2.0, which is 5.0/2.5). However, here’s what we’re actually computing:

(5 × 100) / (2.5 × 100)
            =
         500/250
            =
            2

At first blush this may look correct, but don’t forget that the result is really 0.02 after you factor in the scaling operation. The result we really need is 200 (2.0). The problem here, of course, is that the division by the scaling factor eliminates the scaling factor in the final result. Therefore, to properly compute the result, we actually need to compute k = 100 * m/n so that the result is correct.

Multiplication and division place a limit on the precision you have available. If you have to premultiply the dividend by 100, then the dividend must be at least 100 times smaller than the largest possible integer value or an overflow will occur (producing an incorrect result). Likewise, when multiplying two scaled values, the final result must be 100 times less than the maximum integer value or an overflow will occur. Because of these issues, you may need to set aside additional bits or work with small numbers when using scaled numeric representation.

One big problem with the fractional representations we’ve seen is that they are not exact; that is, they provide a close approximation of real values, but they cannot provide an exact representation for all rational values.^[5] For example, in binary or decimal you cannot exactly represent the value ¹/₃. You could switch to a ternary (base-3) numbering system and exactly represent ¹/₃, but then you wouldn’t be able to exactly represent fractional values like ¹/₂ or ¹/₁₀. What we need is a numbering system that can represent any reasonable fractional value. Rational representation is a possibility in such situations.

Rational representation uses pairs of integers to represent fractional values. One integer represents the numerator (n) of a fraction, and the other represents the denominator (d). The actual value is equal to n/d. As long as n and d are “relatively prime” with respect to one another (that is, they are not both evenly divisible by the same value) this scheme provides a good representation for fractional values within the bounds of the integer representation you’re using for n and d. In theory, arithmetic is quite easy; you use the same algorithms to add, subtract, multiply, and divide fractional values that you learned in grade school when dealing with fractions. The only problem is that certain operations may produce really large numerators or denominators (to the point where you get integer overflow in these values). Other than this problem, however, you can represent a wide range of fractional values using this scheme.

Donald Knuth’s The Art of Computer Programming, Volume Two: Seminumerical Algorithms is probably the seminal text on number systems and arithmetic. For more information on binary, decimal, fixed-point, rational, and floating-point arithmetic, you’ll want to take a look at that text.