19.1 Introduction

In Chapter 14, the schedule design problem is described as an extension of the basic fleet assignment model (FAM). The problem allows flight schedule modification in terms of flight additions, flight deletions, and departure time adjustment for a limited number of flights. One main limitation of this approach is the lack of demand–supply interactions. In other words, it is assumed that the demand is constant and independent of any suggested schedule changes. However, if a flight is eliminated in a city‐pair, the passenger demand is expected to shift to other existing flights/itineraries serving that city‐pair. Similarly, adding a flight to the schedule might induce new demand and/or shift existing demand from other flights/itineraries to the new flight. A change in the demand pattern is also expected with any change in the departure time of the flights. Of course, one should expect that if a significant change is introduced to the schedule, the impact on the demand estimated for each flight would also be significant. As such, assuming fixed flight demand simplifies the integrated schedule design and fleet assignment problem. Disregarding this assumption would require the capability to predict how the demand is redistributed among the different itineraries/flights as a result of any proposed schedule modification.

In this chapter, the itinerary‐based fleet assignment model (IFAM) presented in Chapter 16 is extended to solve the integrated schedule design and fleet assignment problem. The main contribution over the methodology presented in Chapter 14 is that the interaction between flight demand and supply is considered. The methodology simultaneously seeks to optimize the selection of the flights and the assignment of fleet to the selected flights. The discussion of this chapter is based on the work presented by Lohatepanont and Barnhart (2004), which is also adopted as basis for schedule design and FAM developed by several major airlines.

Following this approach, the set of flights proposed by the airline in a future schedule is categorized in two groups, namely, (i) mandatory flights and (ii) optional flights. The mandatory flights are flights that the airline is certain about including them in its future schedule as they are historically shown to be profitable flights. On the other hand, the profitability of the optional flights is uncertain, and hence they might or might not be included in the schedule. The mandatory flights and the optional flights are joined together to form a master flight list. The objective of the problem is to find which of the optional flights are worth including in the future schedule and to determine the optimal fleet assignment decisions for the mandatory flights and the selected optional flights.

19.2 Example of Demand and Supply Interactions

In Chapter 3, we presented several examples to illustrate the interaction among the different planning decisions including determining the flight frequency in the market, specifying the departure time for each flight, and assigning the optimal fleet for each flight. These examples illustrate the effect of supply‐related decisions such as flight frequency (i.e. flight addition/deletion) and flight departure times on the demand of a flight/itinerary. This section extends the discussion in Chapter 3 to illustrate the supply and demand interaction in an airline network.

As explained earlier, on the demand side, the unconstrained demand in any city‐pair is defined as the number of passengers traveling between the city‐pair, assuming unlimited seat capacity. Passengers choose among nonstop and connecting itineraries scheduled in the city‐pair. Given the share of each itinerary, the demand is then determined at the flight level, in order for the airlines to match this demand with the appropriate fleet type (i.e. number of seats). If the assigned capacity is less than the unconstrained demand, the actual demand is set to be equal to the flight capacity. In this case, some demand is spilled, and the airline attempts to recapture this spilled demand by other itineraries. On the supply side, airlines serve the different city‐pairs either by nonstop or connecting itineraries. Major airlines adopt a hub‐and‐spoke network structure to serve connecting traffic through the hubs. Airlines design time banks at the hub to create efficient connecting itineraries. A time bank is defined as a set of flight arrivals to the hub followed by a set of flight departures from the hub.

Figure 19.1 shows an example of a hypothetical airline with a major hub at ATL. The airline serves ten spoke cities in a single time bank. For example, passengers can select to fly between MCO and PHL by connecting at ATL using itinerary MCO‐ATL‐PHL. As explained earlier in Chapter 2, the demand on each flight consists of local and connecting traffic. For example, the demand of the ATL‐PHL flight consists of passengers traveling in the ATL‐PHL market and connecting passengers traveling in the markets TPA‐PHL, JAX‐PHL, MCO‐PHL, FLL‐PHL, and MIA‐PHL. When a flight is added or removed from the time bank (i.e. change in supply), the demand of some other flights is expected to change. For example, if the FLL‐ATL flight is removed from the schedule, the demand on the ATL‐PHL flight is reduced by the number of passengers traveling from FLL to PHL. Similar effect is expected to all other outbound flights from ATL.

19.3 Aspects of Demand–Supply Interactions: Demand Correction Factors

Two aspects should be considered while studying the demand–supply interactions. The first aspect is related to the relationship between the unconstrained demand and changes in the service supply. As discussed in Chapter 3, the demand is not linearly proportional to the service frequency provided in a market. Adding a flight in a market attracts demand to that flight and also induces additional demand for the existing itineraries. Adding a flight usually creates more attractive itineraries that are likely to be selected by customers and hence increases their demand. The opposite impact occurs when a flight is eliminated.

The second aspect is pertinent to understanding the effect of adding/deleting a flight on the demand of other available itineraries/flights. As discussed in Chapter 8, the unconstrained market share of an itinerary depends on the quality of this itinerary as well as all other itineraries in the market. Thus, adding or removing a flight (itinerary) is expected to change the market share of all itineraries in the city‐pair. The impact of demand change might extend to other city‐pairs as explained in the example given above.

To further explain these two aspects of the problem, consider the hypothetical flight schedule given in Figure 19.2. This schedule serves four stations including MIA, ATL, ORD, and DTW. The city‐pairs are served by nonstop and connecting itineraries. The demand of each itinerary is as given in the figure. In case a, the city‐pair MIA‐ORD is served by three itineraries: the nonstop itinerary F1 (itinerary 1), the connecting itinerary F2–F3 (itinerary 2), and the connecting itinerary F4–F5 (itinerary 3). The total demand in this city‐pair is 267 passengers. In this market, 188 passengers are selecting itinerary 1, 37 passengers are selecting itinerary 2, and 42 passengers are selecting itinerary 3. As shown in case b, the airline eliminated flight F4 (MIA‐ATL) from the schedule, which results in the elimination of itinerary 3 (F4–F5) in the city‐pair MIA‐ORD. Thus, itinerary 3 (F4–F5) lost 42 passengers in the city‐pair MIA‐ORD.

In addition, since the airline now has less presence in the MIA‐ORD market, one might expect shifting of some passengers to other airlines. Assume that eight passengers are lost from itinerary 1 and seven passengers are lost from itinerary 2. Meanwhile, assume 10 passengers (out of the 42 passengers of itinerary 3) are shifted from the removed itinerary (itinerary 3) to itinerary 2. As a result of the flight deletion, itinerary 1 has 180 passengers (188 − 8). Itinerary 2 has 40 passengers (37 − 7 + 10). Accordingly, the total demand in the market becomes 220 passengers (267 − 42 − 15 + 10) or (180 + 40).

Define P^o as the set of itineraries containing the optional flight legs, which is indexed by q. Define also P as the set of itineraries serving a given market including a dummy itinerary representing demand served by other airlines in this market. Define as the change in the demand of itinerary p as a result of the deletion of itinerary q. This variable is also known as the demand correction for itinerary p, when itinerary q is deleted. We also define the variable D_q as the unconstrained demand of itinerary q. Considering the example above, D₃ = 42, , and . The total change in the unconstrained demand in this market due to the deletion of itinerary q can be computed as follows:

For generalization, we define the decision variable z_q that is equal to 1, if itinerary q is included in the proposed schedule, and zero otherwise. Thus, the total change in the unconstrained demand of this market due to the deletion of itinerary q can be determined as follows:

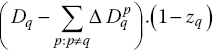
Applying to the example above, the total change (reduction) in the unconstrained demand in city‐pair MIA‐ORD due to the deletion of itinerary 3 is as follows:

The total change in the unconstrained demand in city‐pair MIA‐ORD due to the deletion of itinerary 3 is 47 (i.e. 42 − (−8 + 3) = 47).

Consider the variable fare_q to represent the fare of itinerary q. The corresponding loss of revenue due to the deletion of itinerary q city‐pair can be calculated as the revenue loss due to the deletion of the itinerary minus the revenue recaptured on other itineraries as follows:

Assume that the fares of itineraries 1, 2, and 3 are $270, $165, and $178, respectively. The loss of the unconstrained revenue in the city‐pair MIA‐ORD due to the deletion of itinerary 3 can be calculated as follows:

In the discussion above, the impact of the deletion of itinerary F4–F5 is calculated. However, it should be noted that the impact of the deletion of flight F4 extends to all city‐pairs that are served by itineraries that include flight F4. When flight F4 is removed from the schedule, the nonstop itinerary F4 in city‐pair MIA‐ATL, the single‐stop itinerary F4–F6 in the city‐pair MIA‐DTW, and the single‐stop itinerary F4–F5 in the city‐pair MIA‐ORD no longer exist. Thus, the impact of the deletion of flight F4 should be considered in all three city‐pairs that are served by itineraries that include flight F4.

Define the set P^o as the set of itineraries containing the removed flight F4 (this set of itineraries is indexed by q). In the above example, the set P^o contains three itineraries F4, F4–F5, and F4–F6. Thus, the impact of the deletion of a flight, in terms of the change of the unconstrained revenue ∆R, can be represented mathematically as follows:

Assume in the example above that flight F3 is also removed. This deletion implies that itinerary 2 in the city‐pair MIA‐ORD is removed. As a result of this deletion, we assume = 25, that is, 25 of the 40 passengers of itinerary 2 are shifted to itinerary 1 (the other 15 passengers are assumed to be assigned to the dummy itinerary). Thus, the impact of the deletion of itinerary 3 and itinerary 2 on the demand of itinerary 1 can be calculated as follows:

The demand of itinerary 1 after the deletion of itineraries 2 and 3 is 188 + 17 = 205.

If several itineraries are deleted in a given city‐pair (each itinerary is denoted by q), the impact of the deletion of these itineraries on the demand of an itinerary p ∈ P can be calculated as follows:

In the above example, the city‐pair MIA‐DTW has two itineraries, namely, itinerary 7 and itinerary 8. Itinerary 7 is a single‐stop itinerary composed of flights F1 and F7, while itinerary 8 is a nonstop itinerary using flight F8. Assume that the unconstrained demand of itinerary 7 is 35 passengers and that of itinerary 8 is 70 passengers. Assume that itinerary 8 is an optional itinerary and is removed from the network. We further assume that 47 passengers are shifted from itinerary 8 to itinerary 7 (i.e.  = 47).

One might be interested to estimate the impact of the deletion of itineraries at the flight level rather than at the itinerary level. For example, flight F1 is part of itineraries 1 and 7. The change in the demand of flight 1 due to the deletion of itineraries 2 and 3 in city‐pair MIA‐ORD and the deletion of itinerary 8 in city‐pair MIA‐DTW is computed as follows:

Thus, the demand correction for a flight f that is part of itinerary p ∈ P resulting from the deletion of optional itineraries q ∈ P^o can be expressed mathematically as follows:

where is equal to 1, if itinerary p includes flight leg f, and zero otherwise. In the above example, and .

Finally, it should be noted that the estimation of ∆R requires knowledge of the value D_q, which is the unconstrained demand of each itinerary q ∈ P^o. In addition, there should be a mechanism to estimate the impact of the deletion of an itinerary q ∈ P^o on the unconstrained demand of other itineraries p in the same city‐pair. The values D_q and are expected to get different values for each schedule proposed by the airline.

It is important at this stage to distinguish between the demand correction terms defined above and the recapture rate. Both the demand correction term and the recapture rate are used for demand adjustment (i.e. updating the demand of the itineraries). Both factors estimate the demand of alternative itineraries, if a preferred itinerary is longer available (deleted or become full). The main difference is that the demand correction term deals with the unconstrained demand of the city‐pair, while the recapture rate deals with the constrained demand. The demand correction term estimates the change in the unconstrained demand of an itinerary, when an alternative itinerary is eliminated. The recapture rate, on the other hand, attempts to relocate passengers on alternative itineraries, when the desired itinerary is full. The alternative itineraries should have enough seats to accommodate these passengers. The recapture rate does not impact the total unconstrained demand of the itinerary or the city‐pair.

19.4 The Schedule Design and Adjustment Problem

19.4.1 The Objective Function of ISD‐IFAM

The objective function of the ISD‐IFAM problem is similar to the objective function of the IFAM problem presented in Chapter 16, with an additional term added to consider minimizing the unconstrained revenue loss due to flight deletion. Accordingly, the objective function can be represented mathematically as follows:

where R is the total unconstrained revenue, S is the revenue spilled due to limited seat capacity on some itineraries, M is the portion of the spilled revenue that could be recaptured on other alternative itineraries, C is the operation cost, and ∆R is the unconstrained revenue loss due to flight deletion. Since the total unconstrained revenue is constant, an equivalent cost‐minimizing objective function can be written as follows:

Following the notations presented in Chapter 16, the objective function can be written in a detailed format as follow:

19.4.2 The Constraints of the ISD‐IFAM

The constraints of the ISD‐IFAM problem are similar to those considered for the FAM and the IFAM problems. They include the coverage, balance, and aircraft availability constraints. One difference is that the coverage constraints are different between mandatory and optional flights. Define L^F and L^O as the sets of mandatory and optional flights, respectively. Each of these sets is indexed by f. The coverage constraints of the mandatory flights, which ensure that each flight is assigned to one fleet type, are written as follows:

The coverage constraints of the optional flights are written as shown below. If an option flight f is selected as part of the schedule, a fleet should be assigned to this flight:

The demand constraints presented in the IFAM problem are extended to consider the demand correction when an optional itinerary is removed from the schedule. The constraints below ensure that for each itinerary p ∈ P, the total number of passengers requesting itinerary p ∈ P and redirected to other itineraries r ∈ P should be less than or equal to the demand of itinerary p plus the demand correction for itinerary p ∈ P due to the deletion of any optional itineraries:

Similarly, the capacity constraints presented in the IFAM problem are extended to consider the demand correction when an optional itinerary is removed from the schedule. The constraints below ensure that the number of passengers of a flight does not exceed the capacity assigned to this flight. For any flight f ∈ F, the difference between the spilled and recaptured demands should exceed the number of passengers that must be spilled from the flight:

where Q_f is the unconstrained demand of flight f ∈ F, in case all itineraries are included in the schedule.

Another two constraints are added, which are pertinent to the decision variable Z_q. As mentioned above, the decision variable z_q is equal to 1, if itinerary q is included in the proposed schedule, and zero otherwise. Accordingly, constraints are added to ensure that Z_q is set to zero if at least one flight in itinerary q is eliminated. These constraints can be written as follows:

where L(q) is the set of flight legs in itinerary q.

In the above example, itinerary 3 is composed of two flights, F4 and F5. Thus, two constraints need to be considered for itinerary 3:

Since flight F4 is removed and not assigned to any fleet (i.e. ), it implies that Z_{itinerary 3} = 0, that is, itinerary 3 is also eliminated.

Other constraints are added to ensure that Z_q is equal to 1 in case all flights in itinerary q are considered to be part of the schedule:

where N_q is the number of flight legs in itinerary q.

In the above example, itinerary 7 has two flights, which are F1 and F7 (i.e. N_q = 2). Thus, the right‐hand side is equal to −1. If flights F1 and F7 of itinerary 7 are considered in the schedule, the sum , which is , is equal to 2. Thus, Z₇ should be equal to 1. On the other hand, if and/or , Z₇ should be set to zero to satisfy the constraint above for itinerary 7.