CHAPTER 19

Public-Key Algorithms

19.1 BACKGROUND

The concept of public-key cryptography was invented by Whitfield Diffie and Martin Hellman, and independently by Ralph Merkle. Their contribution to cryptography was the notion that keys could come in pairs—an encryption key and a decryption key—and that it could be infeasible to generate one key from the other (see Section 2.5). Diffie and Hellman first presented this concept at the 1976 National Computer Conference [495]; a few months later, their seminal paper “New Directions in Cryptography” was published [496]. (Due to a glacial publishing process, Merlcle's first contribution to the field didn't appear until 1978 [1064].)

Since 1976, numerous public-key cryptography algorithms have been proposed. Many of these are insecure. Of those still considered secure, many are impractical. Either they have too large a key or the ciphertext is much larger than the plaintext.

Only a few algorithms are both secure and practical. These algorithms are generally based on one of the hard problems discussed in Section 11.2. Of these secure and practical public-key algorithms, some are only suitable for key distribution. Others are suitable for encryption (and by extension for key distribution). Still others are only useful for digital signatures. Only three algorithms work well for both encryption and digital signatures: RSA, ElGamal, and Rabin. All of these algorithms are slow. They encrypt and decrypt data much more slowly than symmetric algorithms; usually that's too slow to support bulk data encryption.

Hybrid cryptosystems (see Section 2.5) speed things up: A symmetric algorithm with a random session key is used to encrypt the message, and a public-key algorithm is used to encrypt the random session key.

Security of Public-Key Algorithms

Since a cryptanalyst has access to the public key, he can always choose any message to encrypt. This means that a cryptanalyst, given C = E_K(P), can guess the value of P and easily check his guess. This is a serious problem if the number of possible plaintext messages is small enough to allow exhaustive search, but can be solved by padding messages with a string of random bits. This makes identical plaintext messages encrypt to different ciphertext messages. (For more about this concept see Section 23.15.)

This is especially important if a public-key algorithm is used to encrypt a session key. Eve can generate a database of all possible session keys encrypted with Bob's public key. Sure, this requires a large amount of time and memory, but for a 40-bit exportable key or a 56-bit DES key, it's a whole lot less time and memory than breaking Bob's public key. Once Eve has generated the database, she will have his key and can read his mail at will.

Public-key algorithms are designed to resist chosen-plaintext attacks; their security is based both on the difficulty of deducing the secret key from the public key and the difficulty of deducing the plaintext from the ciphertext. However, most public-key algorithms are particularly susceptible to a chosen-ciphertext attack (see Section 1.1).

In systems where the digital signature operation is the inverse of the encryption operation, this attack is impossible to prevent unless different keys are used for encryption and signatures.

Consequently, it is important to look at the whole system and not just at the individual parts. Good public-key protocols are designed so that the various parties can't decrypt arbitrary messages generated by other parties—the proof-of-identity protocols are a good example (see Section 5.2).

19.2 KNAPSACK ALGORITHMS

The first algorithm for generalized public-key encryption was the knapsack algorithm developed by Ralph Merkle and Martin Hellman [713,1074]. It could only be used for encryption, although Adi Shamir later adapted the system for digital signatures [1413]. Knapsack algorithms get their security from the knapsack problem, an NP-complete problem. Although this algorithm was later found to be insecure, it is worth examining because it demonstrates how an NP-complete problem can be used for public-key cryptography.

The knapsack problem is a simple one. Given a pile of items, each with different weights, is it possible to put some of those items into a knapsack so that the knapsack weighs a given amount? More formally: Given a set of values M₁, M₂, . . ., M_n, and a sum S, compute the values of b_i such that

The values of b_i can be either zero or one. A one indicates that the item is in the knapsack; a zero indicates that it isn't.

For example, the items might have weights of 1, 5, 6, 11, 14, and 20. You could pack a knapsack that weighs 22; use weights 5, 6, and 11. You could not pack a knapsack that weighs 24. In general, the time required to solve this problem seems to grow exponentially with the number of items in the pile.

The idea behind the Merkle-Hellman knapsack algorithm is to encode a message as a solution to a series of knapsack problems. A block of plaintext equal in length to the number of items in the pile would select the items in the knapsack (plaintext bits corresponding to the b values), and the ciphertext would be the resulting sum. Figure 19.1 shows a plaintext encrypted with a sample knapsack problem.

The trick is that there are actually two different knapsack problems, one solvable in linear time and the other believed not to be. The easy knapsack can be modified to create the hard knapsack. The public key is the hard knapsack, which can easily be used to encrypt but cannot be used to decrypt messages. The private key is the easy knapsack, which gives an easy way to decrypt messages. People who don't know the private key are forced to try to solve the hard knapsack problem.

Superincreasing Knapsacks

What is the easy knapsack problem? If the list of weights is a superincreasing sequence, then the resulting knapsack problem is easy to solve. A superincreasing sequence is a sequence in which every term is greater than the sum of all the previous terms. For example, {1,3,6,13,27,52} is a superincreasing sequence, but {1,3,4,9,15,25} is not.

The solution to a superincreasing knapsack is easy to find. Take the total weight and compare it with the largest number in the sequence. If the total weight is less than the number, then it is not in the knapsack. If the total weight is greater than or equal to the number, then it is in the knapsack. Reduce the weight of the knapsack by the value and move to the next largest number in the sequence. Repeat until finished. If the total weight has been brought to zero, then there is a solution. If the total weight has not, there isn't.

For example, consider a total knapsack weight of 70 and a sequence of weights of {2,3,6,13,27,52}. The largest weight, 52, is less than 70, so 52 is in the knapsack. Subtracting 52 from 70 leaves 18. The next weight, 27, is greater than 18, so 27 is not in the knapsack. The next weight, 13, is less than 18, so 13 is in the knapsack. Subtracting 13 from 18 leaves 5. The next weight, 6, is greater than 5, so 6 is not in the knapsack. Continuing this process will show that both 2 and 3 are in the knapsack and the total weight is brought to 0, which indicates that a solution has been found. Were this a Merkle-Hellman knapsack encryption block, the plaintext that resulted from a ciphertext value of 70 would be 110101.

Non-superincreasing, or normal, knapsacks are hard problems; they have no known quick algorithm. The only known way to determine which items are in the knapsack is to methodically test possible solutions until you stumble on the correct one. The fastest algorithms, taking into account the various heuristics, grow exponentially with the number of possible weights in the knapsack. Add one item to the sequence of weights, and it takes twice as long to find the solution. This is much more difficult than a superincreasing knapsack where, if you add one more weight to the sequence, it simply takes another operation to find the solution.

Figure 19.1 Encryption with knapsacks.

The Merkle-Hellman algorithm is based on this property. The private key is a sequence of weights for a superincreasing knapsack problem. The public key is a sequence of weights for a normal knapsack problem with the same solution. Merkle and Hellman developed a technique for converting a superincreasing knapsack problem into a normal knapsack problem. They did this using modular arithmetic.

Creating the Public Key from the Private Key

Without going into the number theory, this is how the algorithm works: To get a normal knapsack sequence, take a superincreasing knapsack sequence, for example {2,3,6,13,27,52}, and multiply all of the values by a number n, mod m. The modulus should be a number greater than the sum of all the numbers in the sequence: for example, 105. The multiplier should have no factors in common with the modulus: for example, 31. The normal knapsack sequence would then be

The knapsack would then be {62,93,81,88,102,37}.

The superincreasing knapsack sequence is the private key. The normal knapsack sequence is the public key.

Encryption

To encrypt a binary message, first break it up into blocks equal to the number of items in the knapsack sequence. Then, allowing a one to indicate the item is present and a zero to indicate that the item is absent, compute the total weights of the knapsacks—one for every message block.

For example, if the message were 011000110101101110 in binary, encryption using the previous knapsack would proceed like this:

The ciphertext would be

Decryption

A legitimate recipient of this message knows the private key: the original super-increasing knapsack, as well as the values of n and m used to transform it into a normal knapsack. To decrypt the message, the recipient must first determine n⁻¹ such that n(n⁻¹) ≡ 1 (mod m). Multiply each of the ciphertext values by n⁻¹ mod m, and then partition with the private knapsack to get the plaintext values.

In our example, the superincreasing knapsack is {2,3,6,13,27,52}, m is equal to 105, and n is equal to 31. The ciphertext message is 174,280,333. In this case n⁻¹ is equal to 61, so the ciphertext values must be multiplied by 61 mod 105.

The recovered plaintext is 011000 110101 101110.

Practical Implementations

With a knapsack sequence of only six items, it's not hard to solve the problem even if it isn't superincreasing. Real knapsacks should contain at least 250 items. The value for each term in the superincreasing knapsack should be somewhere between 200 and 400 bits long, and the modulus should be somewhere between 100 to 200 bits long. Real implementations of the algorithm use random-sequence generators to produce these values.

With knapsacks like that, it's futile to try to solve them by brute force. If a computer could try a million possibilities per second, trying all possible knapsack values would take over 10⁴⁶ years. Even a million machines working in parallel wouldn't solve this problem before the sun went nova.

Security of Knapsacks

It wasn't a million machines that broke the knapsack cryptosystem, but a pair of cryptographers. First a single bit of plaintext was recovered [725]. Then, Shamir showed that knapsacks can be broken in certain circumstances [1415,1416]. There were other results—[1428,38,754,516,488]—but no one could break the general Merkle-Hellman system. Finally, Shamir and Zippel [1418,1419,1421] found flaws in the transformation that allowed them to reconstruct the superincreasing knapsack from the normal knapsack. The exact arguments are beyond the scope of this book, but a nice summary of them can be found in [1233,1244]. At the conference where the results were presented, the attack was demonstrated on stage using an Apple II computer [492,494].

Knapsack Variants

Since the original Merkle-Hellman scheme was broken, many other knapsack systems have been proposed: multiple iterated knapsacks, Graham-Shamir knapsacks, and others. These have all been analyzed and broken, generally using the same cryptographic techniques, and litter the cryptographic highway [260,253,269,921,15,919,920,922,366,254,263,255]. Good overviews of these systems and their cryptanalyses can be found in [267,479,257,268].

Other algorithms have been proposed that use ideas similar to those used in knapsack cryptosystems, but these too have been broken. The Lu-Lee cryptosystem [990,13] was broken in [20,614,873]; a modification [507] is also insecure [1620]. Attacks on the Goodman-McAuley cryptosystem are in [646,647,267,268]. The Pieprzyk cryptosystem [1246] can be broken by similar attacks. The Niemi cryptosystem [1169], based on modular knapsacks, was broken in [345,788]. A newer multistage knapsack [747] has not yet been broken, but I am not optimistic. Another variant is [294].

While a variation of the knapsack algorithm is currently secure—the Chor-Rivest knapsack [356], despite a “specialized attack” [743]—the amount of computation required makes it far less useful than the other algorithms discussed here. A variant, called the Powerline System, is not secure [958]. Most important, considering the ease with which all the other variations fell, it doesn't seem prudent to trust them.

Patents

The original Merlcle-Hellman algorithm is patented in the United States [720] and worldwide (see Table 19.1). Public Key Partners (PKP) licenses the patent, along with other public-key cryptography patents (see Section 25.5). The U.S. patent will expire on August 19, 1997.

19.3 RSA

Soon after Merkle's knapsack algorithm came the first full-fledged public-key algorithm, one that works for encryption and digital signatures: RSA [1328,1329]. Of all the public-key algorithms proposed over the years, RSA is by far the easiest to understand and implement. (Martin Gardner published an early description of the algorithm in his “Mathematical Games” column in Scientific American [599].) It is also the most popular. Named after the three inventors—Ron Rivest, Adi Shamir, and Leonard Adleman—it has since withstood years of extensive cryptanalysis. Although the cryptanalysis neither proved nor disproved RSA's security, it does suggest a confidence level in the algorithm.

Table 19.1 Foreign Merkle-Hellman Knapsack Patents

RSA gets its security from the difficulty of factoring large numbers. The public and private keys are functions of a pair of large (100 to 200 digits or even larger) prime numbers. Recovering the plaintext from the public key and the ciphertext is conjectured to be equivalent to factoring the product of the two primes.

To generate the two keys, choose two random large prime numbers, p and q. For maximum security, choose p and q of equal length. Compute the product:

Then randomly choose the encryption key, e, such that e and (p − 1)(q − 1) are relatively prime. Finally, use the extended Euclidean algorithm to compute the decryption key, d, such that

In other words,

Note that d and n are also relatively prime. The numbers e and n are the public key; the number d is the private key. The two primes, p and q, are no longer needed. They should be discarded, but never revealed.

To encrypt a message m, first divide it into numerical blocks smaller than n (with binary data, choose the largest power of 2 less than n). That is, if both p and q are 100-digit primes, then n will have just under 200 digits and each message block, m_i, should be just under 200 digits long. (If you need to encrypt a fixed number of blocks, you can pad them with a few zeros on the left to ensure that they will always be less than n.) The encrypted message, c, will be made up of similarly sized message blocks, c_i, of about the same length. The encryption formula is simply

To decrypt a message, take each encrypted block c_i and compute

Since

the formula recovers the message. This is summarized in Table 19.2.

The message could just as easily have been encrypted with d and decrypted with e; the choice is arbitrary. I will spare you the number theory that proves why this works; most current texts on cryptography cover it in detail.

A short example will probably go a long way to making this clearer. If p = 47 and q = 71, then

Table 19.2 RSA Encryption

Public Key: n product of two primes, p and q (p and q must remain secret) e relatively prime to (p − 1 )(q − 1)    Private Key: d e−1 mod ((p − 1)(q − 1))      Encrypting: c = me mod n      Decrypting: m = cd mod n

The encryption key, e, must have no factors in common with

Choose e (at random) to be 79. In that case

This number was calculated using the extended Euclidean algorithm (see Section 11.3). Publish e and n, and keep d secret. Discard p and q.

To encrypt the message

first break it into small blocks. Three-digit blocks work nicely in this case. The message is split into six blocks, m_i, in which

The first block is encrypted as

Performing the same operation on the subsequent blocks generates an encrypted message:

Decrypting the message requires performing the same exponentiation using the decryption key of 1019, so

The rest of the message can be recovered in this manner.

RSA in Hardware

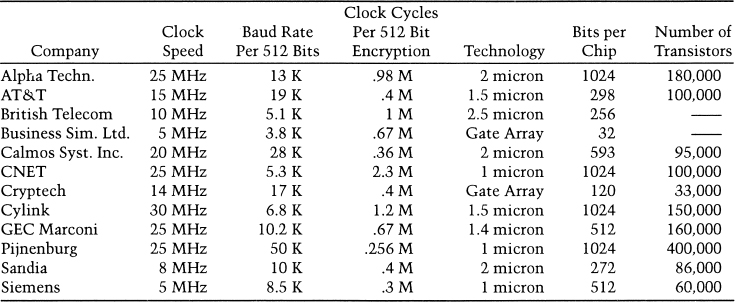
Much has been written on the subject of hardware implementations of RSA [1314, 1474,1456,1316,1485,874,1222,87,1410,1409,1343,998,367,1429,523,772]. Good survey articles are [258,872]. Many different chips perform RSA encryption [1310,252,1101,1317,874,69,737,594,1275,1563,509,1223]. A partial list of currently available RSA chips, from [150,258], is listed in Table 19.3. Not all are available on the open market.

Speed of RSA

In hardware, RSA is about 1000 times slower than DES. The fastest VLSI hardware implementation for RSA with a 512-bit modulus has a throughput of 64 kilobits per second [258]. There are also chips that perform 1024-bit RSA encryption. Currently chips are being planned that will approach 1 megabit per second using a 512-bit modulus; they will probably be available in 1995. Manufacturers have also implemented RSA in smart cards; these implementations are slower.

In software, DES is about 100 times faster than RSA. These numbers may change slightly as technology changes, but RSA will never approach the speed of symmetric algorithms. Table 19.4 gives sample software speeds of RSA [918].

Software Speedups

RSA encryption goes much faster if you're smart about choosing a value of e. The three most common choices are 3, 17, and 65537 (2¹⁶ + 1). (The binary representation of 65537 has only two ones, so it takes only 17 multiplications to exponentiate.) X.509 recommends 65537 [304], PEM recommends 3 [76], and PKCS #1 (see Section 24.14) recommends 3 or 65537 [1345]. There are no security problems with using any of these three values for e (assuming you pad messages with random values—see later section), even if a whole group of users uses the same value for e.

Table 19.3 Existing RSA Chips

Table 19.4 RSA Speeds for Different Modulus Lengths with an 8-bit Public Key (on a SPARC II)

Private key operations can be speeded up with the Chinese remainder theorem if you save the values of p and q, and additional values such as d mod (p − 1), d mod (q − 1), and q⁻¹ mod p [1283,1276]. These additional numbers can easily be calculated from the private and public keys.

Security of RSA

The security of RSA depends wholly on the problem of factoring large numbers. Technically, that's a lie. It is conjectured that the security of RSA depends on the problem of factoring large numbers. It has never been mathematically proven that you need to factor n to calculate m from c and e. It is conceivable that an entirely different way to cryptanalyze RSA might be discovered. However, if this new way allows the cryptanalyst to deduce d, it could also be used as a new way to factor large numbers. I wouldn't worry about it too much.

It is also possible to attack RSA by guessing the value of (p − 1 )(q − 1). This attack is no easier than factoring n [1616].

For the ultraskeptical, some RSA variants have been proved to be as difficult as factoring (see Section 19.5). Also look at [36], which shows that recovering even certain bits of information from an RSA-encrypted ciphertext is as hard as decrypting the entire message.

Factoring n is the most obvious means of attack. Any adversary will have the public key, e, and the modulus, n. To find the decryption key, d, he has to factor n. Section 11.4 discusses the current state of factoring technology. Currently, a 129-decimal-digit modulus is at the edge of factoring technology. So, n must be larger than that. Read Section 7.2 on public key length.

It is certainly possible for a cryptanalyst to try every possible d until he stumbles on the correct one. This brute-force attack is even less efficient than trying to factor n.

From time to time, people claim to have found easy ways to break RSA, but to date no such claim has held up. For example, in 1993 a draft paper by William Payne proposed a method based on Fermat's little theorem [1234]. Unfortunately, this method is also slower than factoring the modulus.

There's another worry. Most common algorithms for computing primes p and q are probabilistic; what happens if p or q is composite? Well, first you can make the odds of that happening as small as you want. And if it does happen, the odds are that encryption and decryption won't work properly—you'll notice right away. There are a few numbers, called Carmichael numbers, which certain probabilistic primality algorithms will fail to detect. These are exceedingly rare, but they are insecure [746]. Honestly, I wouldn't worry about it.

Chosen Ciphertext Attack against RSA

Some attacks work against the implementation of RSA. These are not attacks against the basic algorithm, but against the protocol. It's important to realize that it's not enough to use RSA. Details matter.

Scenario 1: Eve, listening in on Alice's communications, manages to collect a ciphertext message, c, encrypted with RSA in her public key. Eve wants to be able to read the message. Mathematically, she wants m, in which

To recover m, she first chooses a random number, r, such that r is less than n. She gets Alice's public key, e. Then she computes

If x = r^e mod n, then r = x^d mod n.

Now, Eve gets Alice to sign y with her private key, thereby decrypting y. (Alice has to sign the message, not the hash of the message.) Remember, Alice has never seen y before. Alice sends Eve

Now, Eve computes

Eve now has m.

Scenario 2: Trent is a computer notary public. If Alice wants a document notarized, she sends it to Trent. Trent signs it with an RSA digital signature and sends it back. (No one-way hash functions are used here; Trent encrypts the entire message with his private key.)

Mallory wants Trent to sign a message he otherwise wouldn't. Maybe it has a phony timestamp; maybe it purports to be from another person. Whatever the reason, Trent would never sign it if he had a choice. Let's call this message m′.

First, Mallory chooses an arbitrary value x and computes y = x^e mod n. He can easily get e; it's Trent's public key and must be public to verify his signatures. Then he computes m = ym′ mod n, and sends m to Trent to sign. Trent returns m′^d mod n. Now Mallory calculates (m^d mod n)x⁻¹ mod n, which equals n′^d mod n and is the signature of m′.

Actually, Mallory can use several methods to accomplish these same things [423,458,486]. The weakness they all exploit is that exponentiation preserves the multiplicative structure of the input. That is:

Scenario 3: Eve wants Alice to sign m₃. She generates two messages, m₁ and m₂, such that

If Eve can get Alice to sign m₁ and m₂, she can calculate m₃:

Moral: Never use RSA to sign a random document presented to you by a stranger. Always use a one-way hash function first. The ISO 9796 block format prevents this attack.

Common Modulus Attack on RSA

A possible RSA implementation gives everyone the same n, but different values for the exponents e and d. Unfortunately, this doesn't work. The most obvious problem is that if the same message is ever encrypted with two different exponents (both having the same modulus), and those two exponents are relatively prime (which they generally would be), then the plaintext can be recovered without either of the decryption exponents [1457].

Let m be the plaintext message. The two encryption keys are e₁ and e₂. The common modulus is n. The two ciphertext messages are:

The cryptanalyst knows n, e₁, e₂, c₁, and c₂. Here's how he recovers m.

Since e₁ and e₂ are relatively prime, the extended Euclidean algorithm can find r and s, such that

Assuming r is negative (either r or s has to be, so just call the negative one r), then the extended Euclidean algorithm can be used again to calculate c₁⁻¹. Then

There are two other, more subtle, attacks against this type of system. One attack uses a probabilistic method for factoring n. The other uses a deterministic algorithm for calculating someone's secret key without factoring the modulus. Both attacks are described in detail in [449].

Moral: Don't share a common n among a group of users.

Low Encryption Exponent Attack against RSA

RSA encryption and signature verification are faster if you use a low value for e, but that can also be insecure [704]. If you encrypt e(e + 1)/2 linearly dependent messages with different public keys having the same value of e, there is an attack against the system. If there are fewer than that many messages, or if the messages are unrelated, there is no problem. If the messages are identical, then e messages are enough. The easiest solution is to pad messages with independent random values. This also ensures that m^e mod n ≠ m^e. Most real-world RSA implementations—PEM and PGP (see Sections 24.10 and 24.12), for example—do this.

Moral: Pad messages with random values before encrypting them; make sure m is about the same size as n.

Low Decryption Exponent Attack against RSA

Another attack, this one by Michael Wiener, will recover d, when d is up to one quarter the size of n and e is less than n [1596]. This rarely occurs if e and d are chosen at random, and cannot occur if e has a small value.

Moral: Choose a large value for d.

Lessons Learned

Judith Moore lists several restrictions on the use of RSA, based on the success of these attacks [1114,1115]:

• Knowledge of one encryption/decryption pair of exponents for a given modulus enables an attacker to factor the modulus.
• Knowledge of one encryption/decryption pair of exponents for a given modulus enables an attacker to calculate other encryption/decryption pairs without having to factor n.
• A common modulus should not be used in a protocol using RSA in a communications network. (This should be obvious from the previous two points.)
• Messages should be padded with random values to prevent attacks on low encryption exponents.
• The decryption exponent should be large.

Remember, it is not enough to have a secure cryptographic algorithm. The entire cryptosystem must be secure, and the cryptographic protocol must be secure. A failure in any of those three areas makes the overall system insecure.

Attack on Encrypting and Signing with RSA

It makes sense to sign a message before encrypting it (see Section 2.7), but not everyone follows this practice. With RSA, there is an attack against protocols that encrypt before signing [48].

Alice wants to send a message to Bob. First she encrypts it with Bob's public key; then she signs it with her private key. Her encrypted and signed message looks like:

Here's how Bob can claim that Alice sent him m′ and not m. Realize that since Bob knows the factorization of n_B (it's his modulus), he can calculate discrete logarithms with respect to n_B. Therefore, all he has to do is to find an x such that

Then, if he can publish xe_B as his new public exponent and keep n_B as his modulus, he can claim that Alice sent him message m′ encrypted in this new exponent.

This is a particularly nasty attack in some circumstances. Note that hash functions don't solve the problem. However, forcing a fixed encryption exponent for every user does.

Standards

RSA is a de facto standard in much of the world. The ISO almost, but not quite, created an RSA digital-signature standard; RSA is in an information annex to ISO 9796 [762]. The French banking community standardized on RSA [525], as have the Australians [1498]. The United States currently has no standard for public-key encryption, because of pressure from the NSA and patent issues. Many U.S. companies use PKCS (see Section 24.14), written by RSA Data Security, Inc. A draft ANSI banking standard specifies RSA [61].

Patents

The RSA algorithm is patented in the United States [1330], but not in any other country. PKP licenses the patent, along with other public-key cryptography patents (see Section 25.5). The U.S. patent will expire on September 20, 2000.

19.4 POHLIG-HELLMAN

The Pohlig-Hellman encryption scheme [1253] is similar to RSA. It is not a symmetric algorithm, because different keys are used for encryption and decryption. It is not a public-key scheme, because the keys are easily derivable from each other; both the encryption and decryption keys must be kept secret.

Like RSA,

where

Unlike RSA, n is not defined in terms of two large primes, it must remain part of the secret key. If someone had e and n, they could calculate d. Without knowledge of e or d, an adversary would be forced to calculate

We have already seen that this is a hard problem.

Patents

The Pohlig-Hellman algorithm is patented in the United States [722] and also in Canada. PKP licenses the patent, along with other public-key cryptography patents (see Section 25.5).

19.5 RABIN

Rabin's scheme [1283,1601] gets its security from the difficulty of finding square roots modulo a composite number. This problem is equivalent to factoring. Here is one implementation of this scheme.

First choose two primes, p and q, both congruent to 3 mod 4. These primes are the private key; the product n = pq is the public key.

To encrypt a message, M(M must be less than n), simply compute

Decrypting the message is just as easy, but slightly more annoying. Since the receiver knows p and q, he can solve the two congruences using the Chinese remainder theorem. Compute

Then choose an integer a = q(q⁻¹ mod p) and a integer b = p(p⁻¹ mod q). The four possible solutions are:

One of those four results, M₁, M₂, M₃, or M₄, equals M. If the message is English text, it should be easy to choose the correct M_i. On the other hand, if the message is a random-bit stream (say, for key generation or a digital signature), there is no way to determine which M_i is correct. One way to solve this problem is to add a known header to the message before encrypting.

Williams

Hugh Williams redefined Rabin's schemes to eliminate these shortcomings [1601]. In his scheme, p and q are selected such that

and

Also, there is a small integer, S, such that J(S,N) = −1. (J is the Jacobi symbol—see Section 11.3). N and S are public. The secret key is k, such that

To encrypt a message M, compute c₁ such that J(M,N) = (−1)^c₁. Then, compute M′ = (S^c₁ * M) mod N. Like Rabin's scheme, C = M′² mod N. And c₂ = M′ mod 2. The final ciphertext message is the triple:

To decrypt C, the receiver computes M″ using

The proper sign of M″ is given by c₂. Finally,

Williams refined this scheme further in [1603,1604,1605]. Instead of squaring the plaintext message, cube it. The large primes must be congruent to 1 mod 3; otherwise the public and private keys are the same. Even better, there is only one unique decryption for each encryption.

Both Rabin and Williams have an advantage over RSA in that they are provably as secure as factoring. However, they are completely insecure against a chosen-ciphertext attack. If you are going to use these schemes in instances where an attacker can mount this attack (for example, as a digital signature algorithm where an attacker can choose messages to be signed), be sure to use a one-way hash function before signing. Rabin suggested another way of defeating this attack: Append a different random string to each message before hashing and signing. Unfortunately, once you add a one-way hash function to the system it is no longer provably as secure as factoring [628], although adding hashing cannot weaken the system in any practical sense.

Other Rabin variants are [972,909,696,697,1439,989]. A two-dimensional variant is in [866,889].

19.6 ELGAMAL

The E1Gamal scheme [518,519] can be used for both digital signatures and encryption; it gets its security from the difficulty of calculating discrete logarithms in a finite field.

To generate a key pair, first choose a prime, p, and two random numbers, g and x, such that both g and x are less than p. Then calculate

The public key is y, g, and p. Both g and p can be shared among a group of users. The private key is x.

ElGamal Signatures

To sign a message, M, first choose a random number, k, such that k is relatively prime to p − 1. Then compute

and use the extended Euclidean algorithm to solve for b in the following equation:

The signature is the pair: a and b. The random value, k, must be kept secret.

To verify a signature, confirm that

Each ElGamal signature or encryption requires a new value of k, and that value must be chosen randomly. If Eve ever recovers a k that Alice used, she can recover Alice's private key, x. If Eve ever gets two messages signed or encrypted using the same k, even if she doesn't know what it is, she can recover x.

This is summarized in Table 19.5.

For example, choose p = 11 and g = 2. Choose private key x = 8. Calculate

The public key is y = 3, g = 2, and p = 11.

To authenticate M = 5, first choose a random number k = 9. Confirm that gcd(9,10) = 1. Compute

and use the extended Euclidean algorithm to solve for b:

The solution is b = 3, and the signature is the pair: a = 6 and b = 3.

Table 19.5 ElGamal Signatures

Public Key: p prime (can be shared among a group of users) g < p (can be shared among a group of users) y = gx mod p    Private Key: x < p      Signing: k choose at random, relatively prime to p − 1 a (signature) = gk mod p b (signature) such that M = (xa + kb) mod (p − 1)         Verifying: Accept as valid if yaab mod p = gM mod p

To verify a signature, confirm that

A variant of ElGamal for signatures is in [1377]. Thomas Beth invented a variant of the ElGamal scheme suitable for proofs of identity [146]. There are variants for password authentication [312], and for key exchange [773]. And there are thousands more (see Section 20.4).

ElGamal Encryption

A modification of ElGamal can encrypt messages. To encrypt message M, first choose a random k, such that k is relatively prime to p − 1. Then compute

The pair, a and b, is the ciphertext. Note that the ciphertext is twice the size of the plaintext.

To decrypt a and b, compute

Since a^x ≡ g^kx (mod p), and b/a^x ≡ y^kM/a^x ≡ g^xkM/g^xk = M (mod p), this all works (see Table 19.6). This is really the same as Diffie-Hellman key exchange (see Section 22.1), except that y is part of the key, and the encryption is multiplied by y^k.

Speed

Table 19.7 gives sample software speeds of ElGamal [918].

Table 19.6 ElGamal Encryption

Public Key: p prime (can be shared among a group of users) g < p (can be shared among a group of users) y = gx mod p       Private Key: x < p       Encrypting: k choose at random, relatively prime to p − 1. a (ciphertext) = gk mod p b (ciphertext) = ykM mod p     Decrypting: M (plaintext) = b/ax mod p

Patents

ElGamal is unpatented. But, before you go ahead and implement the algorithm, realize that PKP feels that this algorithm is covered under the Diffie-Hellman patent [718]. However, the Diffie-Hellman patent will expire on April 29, 1997, making ElGamal the first public-key cryptography algorithm suitable for encryption and digital signatures unencumbered by patents in the United States. I can hardly wait.

19.7 MCELIECE

In 1978 Robert McEliece developed a public-key cryptosystem based on algebraic coding theory [1041]. The algorithm makes use of the existence of a class of error-correcting codes, known as Goppa codes. His idea was to construct a Goppa code and disguise it as a general linear code. There is a fast algorithm for decoding Goppa codes, but the general problem of finding a code word of a given weight in a linear binary code is NP-complete. A good description of this algorithm can be found in [1233]; see also [1562]. Following is just a quick summary.

Let d_H(x,y) denote the Hamming distance between x and y. The numbers n, k, and t are system parameters.

The private key has three parts: G′ is a k * n generator matrix for a Goppa code that can correct t errors. P is an n * n permutation matrix. S is a k * k nonsingular matrix.

The public key is a k * n matrix G: G = SG′P.

Plaintext messages are strings of k bits, in the form of k-element vectors over GF(2).

To encrypt a message, choose a random n-element vector over GF(2), z, with Hamming distance less than or equal to t.

To decrypt the ciphertext, first compute c′ = cP⁻¹. Then, using the decoding algorithm for the Goppa code, find m′ such that d_H(m′G, c′) is less than or equal to t. Finally, compute m = m′S⁻¹.

In his original paper, McEliece suggested that n = 1024, t = 50, and k = 524. These are the minimum values required for security.

Table 19.7 ElGamal Speeds for Different Modulus Lengths with a 160-bit Exponent (on a SPARC II)

Although the algorithm was one of the first public-key algorithms, and there were no successful cryptanalytic results against the algorithm, it has never gained wide acceptance in the cryptographic community. The scheme is two to three orders of magnitude faster than RSA, but has some problems. The public key is enormous: 2¹⁹ bits long. The data expansion is large: The ciphertext is twice as long as the plaintext.

Some attempts at cryptanalysis of this system can be found in [8,943,1559,306]. None of these were successful in the general case, although the similarity between the McEliece algorithm and knapsacks worried some.

In 1991, two Russian cryptographers claimed to have broken the McEliece system with some parameters [882]. Their paper contained no evidence to substantiate their claim, and most cryptographers discount the result. Another Russian attack, one that cannot be used directly against the McEliece system, is in [1447,1448]. Extensions to McEliece can be found in [424,1227,976].

Other Algorithms Based on Linear Error-Correcting Codes

The Niederreiter algorithm [1167] is closely related to the McEliece algorithm, and assumes that the public key is a random parity-check matrix of an error-correcting code. The private key is an efficient decoding algorithm for this matrix.

Another algorithm, used for identification and digital signatures, is based on syndrome decoding [1501]; see [306] for comments. An algorithm based on error-correcting codes [1621] is insecure [698,33,31,1560,32].

19.8 ELLIPTIC CURVE CRYPTOSYSTEMS

Elliptic curves have been studied for many years and there is an enormous amount of literature on the subject. In 1985, Neal Koblitz and V. S. Miller independently proposed using them for public-key cryptosystems [867,1095]. They did not invent a new cryptographic algorithm with elliptic curves over finite fields, but they implemented existing public-key algorithms, like Diffie-Hellman, using elliptic curves.

Elliptic curves are interesting because they provide a way of constructing “elements” and “rules of combining” that produce groups. These groups have enough familiar properties to build cryptographic algorithms, but they don't have certain properties that may facilitate cryptanalysis. For example, there is no good notion of “smooth” with elliptic curves. That is, there is no set of small elements in terms of which a random element has a good chance of being expressed by a simple algorithm. Hence, index calculus discrete logarithm algorithms do not work. See [1095] for more details.

Elliptic curves over the finite field GF(2ⁿ) are particularly interesting. The arithmetic processors for the underlying field are easy to construct and are relatively simple to implement for n in the range of 130 to 200. They have the potential to provide faster public-key cryptosystems with smaller key sizes. Many public-key algorithms, like Diffie-Hellman, ElGamal, and Schnorr, can be implemented in elliptic curves over finite fields.

The mathematics here are complex and beyond the scope of this book. Those interested in this topic are invited to read the two references previously mentioned, and the excellent book by Alfred Menezes [1059]. Two analogues of RSA work in elliptic curves [890,454]. Other papers are [23,119,1062,869,152,871,892,25,895,353,1061,26,913,914,915]. Elliptic curve cryptosystems with small key lengths are discussed in [701]. Next Computer Inc.'s Fast Elliptic Encryption (FEE) algorithm also uses elliptic curves [388]. FEE has the nice feature that the private key can be any easy-to-remember string. There are proposed public-key cryptosystems using hyper-elliptic curves [868,870,1441,1214].

19.9 LUC

Some cryptographers have developed generalizations of RSA that use various permutation polynomials instead of exponentiation. A variation called Kravitz-Reed, using irreducible binary polynomials [898], is insecure [451,589]. Winfried Müller and Wilfried Nöbauer use Dickson polynomials [1127,1128,965]. Rudolph Lidl and Müller generalized this approach in [966,1126] (a variant is called the Réidi scheme), and Nöbauer looked at its security in [1172,1173]. (Comments on prime generation with Lucas functions are in [969,967,968,598].) Despite all of this prior art, a group of researchers from New Zealand managed to patent this scheme in 1993, calling it LUC [1486,521,1487].

The nth Lucas number, V_n(P, 1), is defined as

There's a lot more theory to Lucas numbers; I'm ignoring all of it. A good theoretical treatment of Lucas sequences is in [1307,1308]. A particularly nice description of the mathematics of LUC is in [1494,708].

In any case, to generate a public-key/private-key key pair, first choose two large primes, p and q. Calculate n, the product of p and q. The encryption key, e, is a random number that is relatively prime to p − 1, q − 1, p + 1, and q + 1.

There are four possible decryption keys,

where lcm is the least common multiple.

The public key is d and n; the private key is e and n. Discard p and q.

To encrypt a message, P (P must be less than n), calculate

And to decrypt:

At best, LUC is no more secure than RSA. And recent, still-unpublished results show how to break LUC in at least some implementations. I just don't trust it.

19.10 FINITE AUTOMATON PUBLIC-KEY CRYPTOSYSTEMS

Chinese cryptographer Tao Renji has developed a public-key algorithm based on finite automata [1301,1302,1303,1300,1304,666]. Just as it is hard to factor the product of two large primes, it is also hard to factor the composition of two finite automata. This is especially so if one or both of them is nonlinear.

Much of this research took place in China in the 1980s and was published in Chinese. Renji is starting to write in English. His main result was that certain nonlinear automata (the quasilinear automata) possess weak inverses if, and only if, they have a certain echelon matrix structure. This property disappears if they are composed with another automaton (even a linear one). In the public-key algorithm, the secret key is an invertible quasilinear automaton and a linear automaton, and the corresponding public key can be derived by multiplying them out term by term. Data is encrypted by passing it through the public automaton, and decrypted by passing it through the inverses of its components (in some cases provided they have been set to a suitable initial state). This scheme works for both encryption and digital signatures.

The performance of such systems can be summed up by saying that like McEliece's system, they run much faster than RSA, but require longer keys. The keylength thought to give similar security to 512-bit RSA is 2792 bits, and to 1024-bit RSA is 4152 bits. For the former case, the system encrypts data at 20,869 bytes/sec and decrypts data at 17,117 bytes/sec, running on a 33 MHz 80486.

Renji has published three algorithms. The first is FAPKC0. This is a weak system which uses linear components, and is primarily illustrative. Two serious systems, FAPKC1 and FAPKC2, use one linear and one nonlinear component each. The latter is more complex, and was developed in order to support identity-based operation.

As for their strength, quite a lot of work has been done on them in China (where there are now over 30 institutes publishing cryptography and security papers). One can see from the considerable Chinese language literature that the problem has been studied.

One possible attraction of FAPKC1 and FAPKC2 is that they are not encumbered by any U.S. patents. Thus, once the Diffie-Hellman patent expires in 1997, they will unquestionably be in the public domain.