
GEDANKEN-EXPERIMENTS ON SEQUENTIAL MACHINES
Edward P. Moore
INTRODUCTION
This paper is concerned with finite automata1 from the
experimental point of view. This does not mean that it reports the
results of any experimentation on actual physical models, hut rather it
is concerned with what kinds of conclusions about the internal conditions
of a finite machine it is possible to draw from external experiments. To
emphasize the conceptual nature of these experiments, the word "gedanken-
experiments" has been borrowed from the physicists for the title.
The sequential machines considered have a finite number of states,
a finite number of possible input symbols, and a finite number of possible
output symbols. The behavior of these machines is strictly deterministic
(i.e., no random elements are permitted in the machines) in that the
present state of a machine depends only on its previous input and previous
state, and the present output depends only on the present state.
The point of view of this paper might also be extended to pro
babilistic machines (such as the noisy discrete channel of communication
O
theory ), but this will not be attempted here.
EXPERIMENTS
There will be two kinds of experiments considered in this paper.
The first of these, called a simple experiment, is depicted in Figure 1 .
1The term "finite" is used to distinguish these automata from Turing
machines [considered in Turing’s "On Computable Numbers, with an
Application to the Entscheidungsproblem", Proc. Lond. Math. Soc.,
(1936) Vol. 24, pp. 230-265] which have an infinitetape, permitting
them to have more complicated behavior than these automata.
^Defined in Shannon’s "A Mathematical Theory of Communication", B.S.T.J.
Vol. 27, p. 4o6 .
i 29

MOORE
FIGURE 1 . Schematic Diagram of a Simple Experiment
A copy of the sequential machine being observed experimentally
will receive successively certain input symbols from the experimenter.
The sequence of output symbols will depend on the sequence of input
symbols (the fact that the correspondence is between sequences rather than
individual symbols is responsible for the terminology "sequential machine")
in a way that depends on which particular sequential machine is present
and its initial state.
The experimenter will choose which finite sequence of input
symbols to put into the machine, either a fixed sequence, or one in which
each symbol depends on the previous output symbols. This sequence of
input symbols, together with the sequence of output symbols, will be called
the outcome of the experiment. In addition there can be a conclusion which
the experimenter emits, the exact nature of which need not be specified.
The conclusion might be thought of as a message typed out on a typewriter,
such as "The machine being experimented on was in state q at the
beginning of the experiment". It is required that the conclusion depend
only on which experiment is being performed and what the sequence of output
symbols was.
The second kind of experiment considered in this paper is the
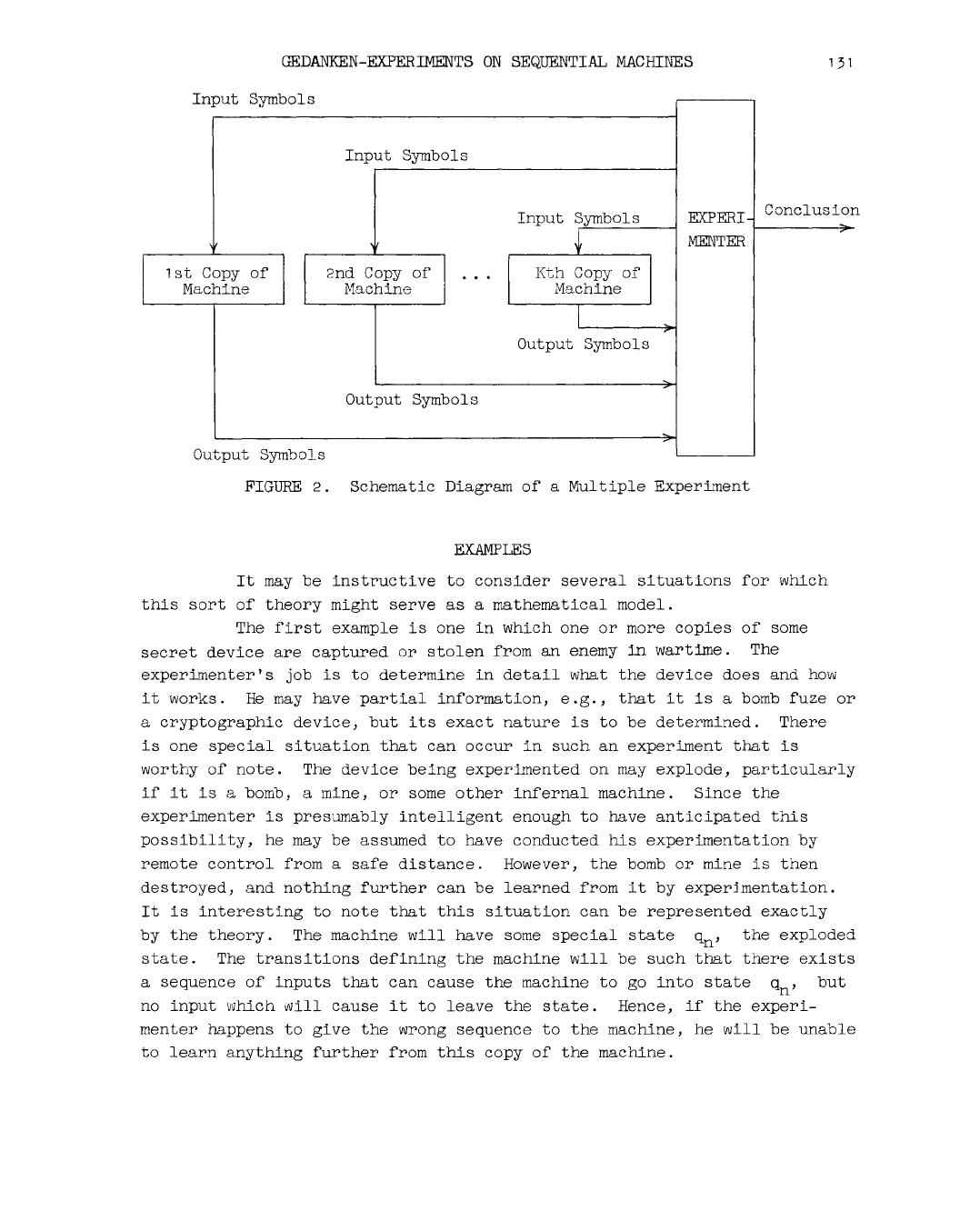
multiple experiment, shown in Figure 2 .
In this case the experimenter has access to several copies of the
same machine, each of which is initially in the same state. The experi
menter can send different sequences of inputs to each of these K copies,
and receive from each the corresponding output sequence.
In each of these two kinds of experiments the experimenter may
be thought of as a human being who is trying to learn the answer to some
question about the nature of the machine or its initial state. This is
not the only kind of experimenter we might imagine in application of this
theory; in particular the experimenter might be another machine. One of
the problems we consider is that of giving explicit instructions for
performing the experiments, and in any case for which this problem is
completely solved it is possible to build a machine which could perform
the experiment.
GEDANKEN-EXFERIMENTS ON SEQUENTIAL MACHINES 1 31
FIGURE 2 . Schematic Diagram of a Multiple Experiment
EXAMPLES
It may be instructive to consider several situations for which
this sort of theory might serve as a mathematical model.
The first example is one in which one or more copies of some
secret device are captured or stolen from an enemy in wartime. The
experimenter1s job is to determine in detail what the device does and how
it works. He may have partial information, e.g., that it is a bomb fuze or
a cryptographic device, but its exact nature is to be determined. There
is one special situation that can occur in such an experiment that is
worthy of note. The device being experimented on may explode, particularly
if it is a bomb, a mine, or some other infernal machine. Since the
experimenter is presumably intelligent enough to have anticipated this
possibility, he may be assumed to have conducted his experimentation by
remote control from a safe distance. However, the bomb or mine is then
destroyed, and nothing further can be learned from it by experimentation.
It is interesting to note that this situation can be represented exactly
by the theory. The machine will have some special state q , the exploded
state. The transitions defining the machine will be such that there exists
a sequence of inputs that can cause the machine to go into state qn , but
no input which will cause it to leave the state. Hence, if the experi
menter happens to give the wrong sequence to the machine, he will be unable
to learn anything further from this copy of the machine.

132
MOORE
There is a somewhat artificial restriction that will be imposed
on the action of the experimenter. He is not allowed to open up the
machine and look at the parts to see what they are and how they are inter
connected. In this military situation, such a restriction might correspond
to the machine being booby trapped so as to destroy itself if tampered with.
It might also correspond to an instance where the components are so
unfamiliar that nothing can be gained by looking at them. At any rate, we
will always impose this somewhat artificial restriction that the machines
under consideration are always just what are sometimes called "black boxes",
described in terms of their inputs and outputs, but no internal construction
information can be gained.
Another application might occur during the course of the design
of actual automata. Suppose an engineer has gone far enough in the design
of some machine intended as a part of a digital computer, telephone central
office, automatic elevator control, etc., to have described his machine in
terms of the list of states and transitions between them, as used in this
paper. He may then wish to perform some gedanken-experiments on his
intended machine. If he can find, for instance, that there is no experi
mental way of distinguishing his design from some machine with fewer
states, he might as well build the simpler machine.
It should be remarked that from this engineering point of view
certain results closely paralleling parts of this paper (notably the
reduction described in Theorem k) have recently been independently found by
D. A. Huffman in his Ph.D. thesis in Electrical Engineering (M.I.T.). His
results are to appear in the Journal of the Franklin Institute.
Still another situation of which this theory is a mathematical
model occurs in the case of the psychiatrist, who experiments on a patient.
He gives the patient inputs (mainly verbal), and notes the outputs (again
mainly verbal), using them to learn what is wrong with the patient. The
black box restriction corresponds approximately to the distinction between
the psychiatrist and the brain surgeon.
Finally, another situation of which this might conceivably be a
mathematical model occurs when a scientist of any sort performs an experi
ment. In physics, chemistry, or almost any other science the inputs which
an experimenter puts into his experiment and the outputs he gets from it
do not correspond exactly to the things the experimenter wishes to learn
by performing the experiment. The experimenter is frequently forced to ask
his questions in indirect form, because of restrictions imposed by
intractable laws of nature. These restrictions are somewhat similar in
their effect on the organization of the experiment to the black box
restriction.

GEDA3MEN-EXPERIME3WS ON SEQUENTIAL MACHINES
133
The analogy between this theory and such scientific experimenta
tion is not as good as in the previous situations, because actual experi
ments may be continuous and probabilistic (rather than finite and
deterministic), and also because the experiment may not be completely
isolated from the experimenter, i.e., the experimenter may be experimenting
on a system of which he himself is a part. However, certain qualitative
results of the theory may be of interest to those who like to speculate
about the basic problems of experimental science.
CONVENTIONS
Each machine will have a finite number n of states, which will
be called q.|, q2, . .., qn a finite number m of possible input symbols
which will be called S 1, S2, ..., Sm , and a finite number p of possible
output symbols, which will be called Sm+1> Sm+2' . ^m+p. In several
examples used in this paper we will have m = 2 , p = 2 , S1 = S^ = 0,
and S2 = S^ = 1 .
Time is assumed to come in discrete steps, so the machine can be
thought of as a synchronous device. Since many of the component parts of
actual automata are variable in their speed, this assumption means the
theory has not been stated in the most general terms. In practice, some
digital computers and most telephone central offices have been designed
asynchronously. However, by providing a central "clock" source of uniform
time intervals It is possible to organize even asynchronous components so
that they act in the discrete time steps of a synchronous machine. Digital
computers and other electronic automata are usually built in this
synchronous fashion. The synchronous convention is used in this paper since
it permits simpler exposition, but the fact that these results can be
translated with very little change into asynchronous terms should be
obvious from the fact that Hoffman wrote his paper in terms of the
asychronous case.
The state that the machine will be in at a given time depends
only on its state at the previous time and the previous input symbol. The
output symbol at a given time depends only on the current state of the
machine. A table used to give these transitions and outputs will be used
as the definition of a machine. To illustrate these conventions, let us
consider the following example of a machine:
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
