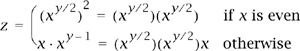This chapter describes the AP interface, which provides signed integers of arbitrary precision and arithmetic operations on them. That is, unlike XP_Ts, the integers provided by AP can be negative or positive, and they can have an arbitrary number of digits. The values that can be represented are limited only by the available memory. These integers can be used in applications that need integer values in a potentially huge range. For example, some mutual-fund companies track share prices to the nearest centicent — 1/10,000 of a dollar — and thus might do all computations in centicents. A 32-bit unsigned integer can represent only $429,496.7295, which is only a tiny fraction of the billions of dollars held by some funds.
AP uses XP, of course, but AP is a high-level interface: It reveals only an opaque type that represents arbitrary-precision signed integers. AP exports functions to allocate and deallocate these integers, and to perform the usual arithmetic operations on them. It also implements the checked runtime errors that XP omits. Most applications should use AP or the MP interface described in the next chapter.
The AP interface hides the representation of an arbitrary-precision signed integer behind an opaque pointer type:
<ap.h>≡ #ifndef AP_INCLUDED #define AP_INCLUDED #include <stdarg.h> #define T AP_T typedef struct T *T; <exported functions 324> #undef T #endif
It is a checked runtime error to pass a null AP_T to any function in this interface, except where noted below.
AP_Ts are created by
<exported functions 324>≡
extern T AP_new (long int n);
extern T AP_fromstr(const char *str, int base,
char **end);AP_new creates a new AP_T, initializes it to the value of n, and returns it. AP_fromstr creates a new AP_T, initializes it to the value specified by str and base, and returns it. AP_new and AP_fromstr can raise Mem_Failed.
AP_fromstr is like strtol in the C library; it interprets the string in str as an integer in base. It ignores leading white space, and accepts an optional sign followed by one or more digits in base. For bases between 11 and 36, AP_fromstr interprets either lowercase or uppercase letters as digits greater than nine. It is a checked runtime error for base to be less than two or more than 36.
If end is nonnull, *end is assigned the pointer to the character that terminated AP_fromstr’s interpretation. If the characters in str do not specify an integer in base, AP_fromstr returns null and sets *end to str, if end is nonnull. It is a checked runtime error for str to be null.
The functions
<exported functions 324>+≡
extern long int AP_toint(T x);
extern char *AP_tostr(char *str, int size,
int base, T x);
extern void AP_fmt(int code, va_list *app,
int put(int c, void *cl), void *cl,
unsigned char flags[], int width, int precision);extract and print the integers represented by AP_Ts. AP_toint returns a long int with the same sign as x and a magnitude equal to |x| mod (LONG_MAX+1), where LONG_MAX is the largest positive long int. If x is LONG_MIN, which is -LONG_MAX-1 on two’s-complement machines, AP_toint returns -((LONG_MAX+1) mod (LONG_MAX+1)), which is zero.
AP_tostr fills str with a null-terminated string that is the character representation of x in base, and returns str. Uppercase letters are used for digits that exceed nine when base exceeds 10. It is a checked runtime error for base to be less than two or more than 36.
If str is nonnull, AP_tostr fills str up to size characters. It is a checked runtime error for size to be too small — that is, for the character representation of x plus a null character to require more than size characters. If str is null, size is ignored; AP_tostr allocates a string large enough to hold the representation of x, and returns that string. It is the client’s responsibility to deallocate the string. When str is null, AP_tostr can raise Mem_Failed.
AP_fmt can be used with the functions in the Fmt interface as a conversion function to format AP_Ts. It consumes an AP_T and formats it according to the optional flags, width, and precision in the same way that the printf specifier %d formats its integer argument. AP_fmt can raise Mem_Failed. It is a checked runtime error for app or flags to be null.
AP_Ts are deallocated by
<exported functions 324>+≡
extern void AP_free(T *z);AP_free deallocates *z and sets *z to null. It is a checked runtime error for z or *z to be null.
The following functions perform arithmetic operations on AP_Ts. Each returns an AP_T for the result, and each can raise Mem_Failed.
<exported functions 324>+≡
extern T AP_neg(T x);
extern T AP_add(T x, T y);
extern T AP_sub(T x, T y);
extern T AP_mul(T x, T y);
extern T AP_div(T x, T y);
extern T AP_mod(T x, T y);
extern T AP_pow(T x, T y, T p);AP_neg returns - x, AP_add returns x+y, AP_sub returns x − y, and AP_mul returns x·y. Here and below, x and y denote the integer values represented by x and y. AP_div returns x/y, and AP_mod returns x mod y. Division truncates to the left: toward minus infinity when one of x or y is negative and toward zero otherwise, so the remainder is always positive. More precisely, the quotient, q, is the maximum integer that does not exceed the real number w such that w · y=x, and the remainder is defined to be x - y·q. This definition is identical to the one implemented by the Arith interface described in Chapter 2. For AP_div and AP_mod, it is a checked runtime error for y to be zero.
AP_pow returns xy when p is null. When p is nonnull, AP_pow returns (xy) mod p. It is a checked runtime error for y to be negative, or for p to be nonnull and less than two.
The convenience functions
<exported functions 324>+≡
extern T AP_addi(T x, long int y);
extern T AP_subi(T x, long int y);
extern T AP_muli(T x, long int y);
extern T AP_divi(T x, long int y);
extern long AP_modi(T x, long int y);are similar to the functions described above but take a long int for y. For example, AP_addi(x, y) is equivalent to AP_add(x, AP_new(y)). The rules regarding division and modulus are the same as for AP_div and AP_mod. Each of these functions can raise Mem_Failed.
AP_Ts can be shifted with the functions
<exported functions 324>+≡
extern T AP_lshift(T x, int s);
extern T AP_rshift(T x, int s);AP_lshift returns an AP_T equal to x shifted left by s bits, which is equivalent to multiplying x by 2s. AP_rshift returns an AP_T equal to x shifted right by s bits, which is equivalent to dividing x by 2s. The values returned by both functions have the same sign as x, unless the shift values are zero, and the vacated bits are set to zero. It is a checked runtime error for s to be negative, and the shift functions can raise Mem_Failed.
AP_Ts are compared by
<exported functions 324>+≡
extern int AP_cmp (T x, T y);
extern int AP_cmpi(T x, long int y);Both functions return an integer less than zero, equal to zero, or greater than zero, if, respectively, x < y, x = y, or x > y.
A calculator that does arbitrary-precision computations illustrates the use of the AP interface. The implementation of the AP interface, described in the next section, illustrates the use of the XP interface.
The calculator, calc, uses Polish suffix notation: Values are pushed onto a stack, and operators pop their operands from the stack and push their results. A value is one or more consecutive decimal digits, and the operators are as follows.
| negation |
| addition |
| subtraction |
| multiplication |
| division |
| remainder |
| exponentiation |
| duplicate the value at the top of the stack |
| print the value at the top of the stack |
| print all the values on the stack from the top down |
| quit |
White-space characters separate values but are otherwise ignored; other characters are announced as unrecognized operators. The size of the stack is limited only by available memory, but a diagnostic announces stack underflow.
calc is a simple program that has three main tasks: interpreting the input, computing values, and managing a stack.
<calc.c>≡ #include <ctype.h> #include <stdio.h> #include <string.h> #include <stdlib.h> #include "stack.h" #include "ap.h" #include "fmt.h" <calc data 328> <calc functions 328>
As the inclusion of stack.h suggests, calc uses the stack interface described in Chapter 2 for its stack:
<calc data 328>≡ Stack_T sp; <initialization 328>≡ sp = Stack_new();
calc must not call Stack_pop when sp is empty, so it wraps all pop operations in a function that checks for underflow:
<calc functions 328>≡
AP_T pop(void) {
if (!Stack_empty(sp))
return Stack_pop(sp);
else {
Fmt_fprint(stderr, "?stack underflow
");
return AP_new(0);
}
}Always returning an AP_T, even when the stack is empty, simplifies error-checking elsewhere in calc.
The main loop in calc reads the next “token” — value or operator — and switches on it:
<calc functions 328>+≡ int main(int argc, char *argv[]) { int c; <initialization 328> while ((c = getchar()) != EOF) switch (c) { <cases 329> default: if (isprint(c)) Fmt_fprint(stderr, "?'%c'", c); else Fmt_fprint(stderr, "?'\%03o'", c); Fmt_fprint(stderr, " is unimplemented "); break; } <clean up and exit 329> } <clean up and exit 329>≡ <clear the stack 333> Stack_free(&sp); return EXIT_SUCCESS;
An input character is either white space, the first digit of a value, an operator, or something else, which is an error as shown in the default case above. White space is simply ignored:
<cases 329>≡
case ' ': case ' ': case '
': case 'f': case '
':
break;A digit is the beginning of a value; calc gathers up the digits that follow the first one into a buffer, and uses AP_fromstr to convert the run of digits to an AP_T:
<cases 329>+≡ case '0': case '1': case '2': case '3': case '4': case '5': case '6': case '7': case '8': case '9': { char buf[512]; <gather up digits into buf 333> Stack_push(sp, AP_fromstr(buf, 10, NULL)); break; }
Each operator pops zero or more operands from the stack and pushes zero or more results. Addition is typical:
<cases 329>+≡ case '+': { <pop x and y off the stack 330> Stack_push(sp, AP_add(x, y)); <free x and y 330> break; } <pop x and y off the stack 330>≡ AP_T y = pop(), x = pop(); <free x and y 330>≡ AP_free(&x); AP_free(&y);
It is easy to make the error of having two or more copies of one AP_T on the stack, which makes it impossible to know which AP_Ts should be freed. The code above shows the simple protocol that avoids this problem: The only “permanent” AP_Ts are those on the stack; all others are freed by calling AP_free.
Subtraction and multiplication are similar in form to addition:
<cases 329>+≡ case '-': { <pop x and y off the stack 330> Stack_push(sp, AP_sub(x, y)); <free x and y 330> break; } case '*': { <pop x and y off the stack 330> Stack_push(sp, AP_mul(x, y)); <free x and y 330> break; }
Division and remainder are also simple, but they must guard against a zero divisor.
<cases 329>+≡ case '/': { <pop x and y off the stack 330> if (AP_cmpi(y, 0) == 0) { Fmt_fprint(stderr, "?/ by 0 "); Stack_push(sp, AP_new(0)); } else Stack_push(sp, AP_div(x, y)); <free x and y 330> break; } case '%': { <pop x and y off the stack 330> if (AP_cmpi(y, 0) == 0) { Fmt_fprint(stderr, "?%% by 0 "); Stack_push(sp, AP_new(0)); } else Stack_push(sp, AP_mod(x, y)); <free x and y 330> break; }
Exponentiation must guard against a nonpositive power:
<cases 329>+≡ case '^': { <pop x and y off the stack 330> if (AP_cmpi(y, 0) <= 0) { Fmt_fprint(stderr, "?nonpositive power "); Stack_push(sp, AP_new(0)); } else Stack_push(sp, AP_pow(x, y, NULL)); <free x and y 330> break; }
Duplicating the value at the top of the stack is accomplished by popping it off the stack, so that underflow is detected, and pushing the value and a copy of the value. The only way to copy an AP_T is to add zero to it.
<cases 329>+≡
case 'd': {
AP_T x = pop();
Stack_push(sp, x);
Stack_push(sp, AP_addi(x, 0));
break;
}Printing an AP_T is accomplished by associating AP_cvt with a format code and using that code in a format string passed to Fmt_fmt; calc uses D.
<initialization 328>+≡ Fmt_register('D', AP_fmt); <cases 329>+≡ case 'p': { AP_T x = pop(); Fmt_print("%D ", x); Stack_push(sp, x); break; }
Printing all the values on the stack reveals a weakness in the Stack interface: There’s no way to access the values under the top one, or to tell how many values are on the stack. A better stack interface might include functions like Table_length and Table_map; without them, calc must create a temporary stack, pour the contents of the main stack onto the temporary stack, printing the values as it goes, and then pour the values from the temporary stack back onto the main stack.
<cases 329>+≡
case 'f':
if (!Stack_empty(sp)) {
Stack_T tmp = Stack_new();
while (!Stack_empty(sp)) {
AP_T x = pop();
Fmt_print("%D
", x);
Stack_push(tmp, x);
}
while (!Stack_empty(tmp))
Stack_push(sp, Stack_pop(tmp));
Stack_free(&tmp);
}
break;The remaining cases negate values, clear the stack, and quit:
<cases 329>+≡ case '~': { AP_T x = pop(); Stack_push(sp, AP_neg(x)); AP_free(&x); break; } case 'c': <clear the stack 333> break; case 'q': <clean up and exit 329> <clear the stack 333>≡ while (!Stack_empty(sp)) { AP_T x = Stack_pop(sp); AP_free(&x); }
calc deallocates the stacked AP_Ts as it clears the stack to avoid creating objects that are unreachable and whose storage could never be deallocated.
The final chunk of calc reads a run of one or more digits into buf:
<gather up digits into buf 333>≡
{
int i = 0;
for ( ; c != EOF && isdigit(c); c = getchar(), i++)
if (i < (int)sizeof (buf) - 1)
buf[i] = c;
if (i > (int)sizeof (buf) - 1) {
i = (int)sizeof (buf) - 1;
Fmt_fprint(stderr,
"?integer constant exceeds %d digits
", i);
}
buf[i] = 0;
if (c != EOF)
ungetc(c, stdin);
}As this code shows, calc announces excessively long numbers and truncates them.
The implementation of the AP interface illustrates a typical use of the XP interface. AP uses a sign-magnitude representation for signed numbers: An AP_T points to a structure that carries the sign of the number and its absolute value as an XP_T:
<ap.c>≡ #include <ctype.h> #include <limits.h> #include <stdlib.h> #include <string.h> #include "assert.h" #include "ap.h" #include "fmt.h" #include "xp.h" #include "mem.h" #define T AP_T struct T { int sign; int ndigits; int size; XP_T digits; }; <macros 337> <prototypes 336> <static functions 335> <functions 335>
sign is either 1 or −1. size is the number of digits allocated and pointed to by digits; it can exceed ndigits, which is the number of digits in use. That is, an AP_T represents the number given by the XP_T in digits[0..ndigits-1]. AP_Ts are always normalized: Their most significant digit is nonzero, unless the value is zero. Thus, ndigits is often less than size. Figure 18.1 shows the layout of an 11-digit AP_T that is equal to 751,702,468,129 on a little endian computer with 32-bit words and 8-bit characters. The unused elements of the digits array are shaded.
<functions 335>≡
T AP_new(long int n) {
return set(mk(sizeof (long int)), n);
}which calls the static function mk to do the actual allocation; mk allocates an AP_T capable of holding size digits and initializes it to zero.
<static functions 335>≡
static T mk(int size) {
T z = CALLOC(1, sizeof (*z) + size);
assert(size > 0);
z->sign = 1;
z->size = size;
z->ndigits = 1;
z->digits = (XP_T)(z + 1);
return z;
}There are two representations for zero in a sign-magnitude representation; by convention, AP uses only the positive representation, as the code in mk suggests.
AP_new calls the static function set to initialize an AP_T to the value of a long int, and, as usual, set handles the most negative long int as a special case:
<static functions 335>+≡
static T set(T z, long int n) {
if (n == LONG_MIN)
XP_fromint(z->size, z->digits, LONG_MAX + 1UL);
else if (n < 0)
XP_fromint(z->size, z->digits, -n);
else
XP_fromint(z->size, z->digits, n);
z->sign = n < 0 ? -1 : 1;
return normalize(z, z->size);
}The assignment to z->sign is the idiom that ensures that the sign value is either 1 or −1, and that the sign of zero is one. An XP_T is unnormalized, because its most significant digit can be zero. When an AP function forms an XP_T that might be unnormalized, it calls normalize to fix it by computing the correct ndigits field:
<static functions 335>+≡ static T normalize(T z, int n) { z->ndigits = XP_length(n, z->digits); return z; } <prototypes 336>≡ static T normalize(T z, int n);
<functions 335>+≡
void AP_free(T *z) {
assert(z && *z);
FREE(*z);
}AP_new is the only way to allocate an AP_T, so it is safe for AP_free to “know” that the space for the structure and the digit array were allocated with a single allocation.
Negation is the easiest arithmetic operation to implement, and it illustrates a recurring problem with a sign-magnitude representation:
<functions 335>+≡ T AP_neg(T x) { T z; assert(x); z = mk(x->ndigits); memcpy(z->digits, x->digits, x->ndigits); z->ndigits = x->ndigits; z->sign = iszero(z) ? 1 : -x->sign; return z; } <macros 337>≡ #define iszero(x) ((x)->ndigits==1 && (x)->digits[0]==0)
Negating x simply copies the value and flips the sign, except when the value is zero. The macro iszero takes advantage of the constraint that AP_Ts are normalized: The value zero has only one digit.
The magnitude of x·y is |x| · |y|, and it might have as many digits as the sum of the number of digits in x and y. The result is positive when x and y have the same sign or when x or y is zero, and negative otherwise. A sign is −1 or 1, so the comparison
<x and y have the same sign 338>≡ ((x->sign^y->sign) == 0)
is true when x and y have the same sign and false otherwise. AP_mul calls XP_mul to compute |x|·|y| and computes the sign itself:
<functions 335>+≡ T AP_mul(T x, T y) { T z; assert(x); assert(y); z = mk(x->ndigits + y->ndigits); XP_mul(z->digits, x->ndigits, x->digits, y->ndigits, y->digits); normalize(z, z->size); z->sign = iszero(z) || <x and y have the same sign 338> ? 1 : -1; return z; }
Recall that XP_mul computes z = z + x·y, and that mk initializes z to both a normalized and an unnormalized zero.
Addition is more complicated, because it may require subtraction, depending on the signs and values of x and y. The following table summarizes the cases.
y< 0 | y≥ 0 | |||
x<0 | −(|x| + |y|) | y − |x| | if y ≥ |x| | |
−(|x| − y) | if y < |x| | |||
x ≥ 0 | x − |y| | if x > |y| | x + y | |
−(|y| − x) | if x ≤ |y| | |||
|x| + |y| is equivalent to x + y, when x and y are nonegative, so the cases on the diagonal can both be handled by computing |x| + |y| and setting the sign to the sign of x. The result may have one more digit than the longest of x and y.
<functions 335>+≡ T AP_add(T x, T y) { T z; assert(x); assert(y); if (<x and y have the same sign 338>) { z = add(mk(maxdigits(x,y) + 1), x, y); z->sign = iszero(z) ? 1 : x->sign; } else <set z to x+y when x and y have different signs 340> return z; } <macros 337>+≡ #define maxdigits(x,y) ((x)->ndigits > (y)->ndigits ? (x)->ndigits : (y)->ndigits)
add calls XP_add to do the actual addition:
<static functions 335>+≡
static T add(T z, T x, T y) {
int n = y->ndigits;
if (x->ndigits < n)
return add(z, y, x);
else if (x->ndigits > n) {
int carry = XP_add(n, z->digits, x->digits,
y->digits, 0);
z->digits[z->size-1] = XP_sum(x->ndigits - n,
&z->digits[n], &x->digits[n], carry);
} else
z->digits[n] = XP_add(n, z->digits, x->digits,
y->digits, 0);
return normalize(z, z->size);
}The first test in add ensures that x is the longer operand. If x is longer than y, XP_add computes the n-digit sum in z->digits[0..n-1] and returns the carry. The sum of this carry and x->digits[n..x->ndigits-1] becomes z->digits[n..z->size-1]. If x and y have the same number of digits, XP_add computes the n-digit sum as in the previous case, and the carry is z’s most significant digit.
The other addition cases can be simplified, too. When x < 0, y ≥ 0, and |x| > |y|, the magnitude of x + y is |x| - |y|, and the sign is negative. When x ≥ 0, y<0, and |x|>|y|, the magnitude of x + y is also |x| − |y|, but the sign is positive. In both cases, the sign of the result is the same as the sign of x. sub, described below, does the subtraction, and cmp compares |x| and |y|. The result may have as many digits as x.
<set z to x+y when x and y have different signs 340>≡ if (cmp(x, y) > 0) { z = sub(mk(x->ndigits), x, y); z->sign = iszero(z) ? 1 : x->sign; }
When x<0, y≥0, and |x|≤|y|, the magnitude of x + y is |y| - |x| and the sign is positive. When x≥0, y<0, and |x|≤|y|, the magnitude of x + y is also |y|-|x|, but the sign is negative. In both of these cases, the sign of the result is the opposite of the sign of x, and it may have as many digits as y.
<set z to x+y when x and y have different signs 340>+≡ else { z = sub(mk(y->ndigits), y, x); z->sign = iszero(z) ? 1 : -x->sign; }
Subtraction benefits from a similar analysis. The following table lays out the cases.
y<0 | y≥0 | |||
x<0 | -(|x| -|y|) | if |x|>|y| | -(|x| + y) | |
|y| - |x| | if |x| ≤|y| | |||
x≥0 | x+|y| | x - y | if x>y | |
-(y - x) | if x≤y | |||
Here, the off-diagonal cases are the easy ones, and both can be handled by computing |x|+|y| and setting the sign of the result to the sign of x:
<functions 335>+≡ T AP_sub(T x, T y) { T z; assert(x); assert(y); if (!<x and y have the same sign 338>) { z = add(mk(maxdigits(x,y) + 1), x, y); z->sign = iszero(z) ? 1 : x->sign; } else <set z to x−y when x and y have the same sign 341> return z; }
The diagonal cases depend on the relative values of x and y. When |x|>|y|, the magnitude of x - y is |x|-|y| and the sign is the same as the sign of x; when |x|≤|y, the magnitude of x - y is |y|-|x| and the sign is the opposite of the sign of x.
<set z to x−y when x and y have the same sign 341>≡ if (cmp(x, y) > 0) { z = sub(mk(x->ndigits), x, y); z->sign = iszero(z) ? 1 : x->sign; } else { z = sub(mk(y->ndigits), y, x); z->sign = iszero(z) ? 1 : -x->sign; }
Like add, sub calls the XP functions to implement subtraction; y never exceeds x.
<static functions 335>+≡
static T sub(T z, T x, T y) {
int borrow, n = y->ndigits;
borrow = XP_sub(n, z->digits, x->digits,
y->digits, 0);
if (x->ndigits > n)
borrow = XP_diff(x->ndigits - n, &z->digits[n],
&x->digits[n], borrow);
assert(borrow == 0);
return normalize(z, z->size);
}When x is longer than y, the call to XP_sub computes the n-digit difference in z->digits[0..n-1] and returns the borrow. The difference between this borrow and x->digits[n..x->ndigits-1] becomes z->digits[n..z->size-1], and the final borrow is zero because |x≥|y| in all calls to sub. If x and y have the same number of digits, XP_sub computes the n-digit difference as in the previous case, but there is no borrow to propagate.
Division is like multiplication, but is complicated by the truncation rules. When x and y have the same sign, the quotient is |x|/|y| and is positive, and the remainder is |x| mod |y|. When x and y have different signs, the quotient is negative; its magnitude is |x/|y| when |x| mod |y| is zero and |x|/|y|+ 1 when |x| mod |y| is nonzero. The remainder is |x| mod |y| when that value is zero and |y| − (|x| mod |y|) when |x| mod |y| is nonzero. The remainder is thus always positive. The quotient and remainder might have as many digits as x and y, respectively.
<functions 335>+≡ T AP_div(T x, T y) { T q, r; <q ← x/y, r ← x mod y 343> if (!<x and y have the same sign 338> && !iszero(r)) { int carry = XP_sum(q->size, q->digits, q->digits, 1); assert(carry == 0); normalize(q, q->size); } AP_free(&r); return q; } <q ← x/y, r ← x mod y 343>≡ assert(x); assert(y); assert(!iszero(y)); q = mk(x->ndigits); r = mk(y->ndigits); { XP_T tmp = ALLOC(x->ndigits + y->ndigits + 2); XP_div(x->ndigits, q->digits, x->digits, y->ndigits, y->digits, r->digits, tmp); FREE(tmp); } normalize(q, q->size); normalize(r, r->size); q->sign = iszero(q) || <x and y have the same sign 338> ? 1 : -1;
AP_div doesn’t bother adjusting the remainder when x and y have different signs because it discards the remainder. AP_mod does just the opposite: It adjusts only the remainder and discards the quotient.
<functions 335>+≡ T AP_mod(T x, T y) { T q, r; <q ← x/y, r ← x mod y 343> if (!<x and y have the same sign 338 > && !iszero(r)) { int borrow = XP_sub(r->size, r->digits, y->digits, r->digits, 0); assert(borrow == 0); normalize(r, r->size); } AP_free(&q); return r; }
AP_pow returns xy when p, the third argument, is null. When p is nonnull, AP_pow returns (xy) mod p.
<functions 335>+≡ T AP_pow(T x, T y, T p) { T z; assert(x); assert(y); assert(y->sign == 1); assert(!p || p->sign==1 && !iszero(p) && !isone(p)); <special cases 344> if (p) <z ← xy mod p 346> else < z ← xy 345> return z; } <macros 337>+≡ #define isone(x) ((x)->ndigits==1 && (x)->digits[0]==1)
To compute z = xy, it’s tempting to set z to one and multiply it by x, y times. The problem is that if y is big, say, 200 decimal digits, this approach takes much longer than the age of the universe. Mathematical rules help simplify the computation:
These rules permit xy to be computed by calling AP_pow recursively and multiplying and squaring the result. The depth of the recursion (and hence the number operations) is proportional to lg y. The recursion bottoms out when x or y is zero or one, because 0y = 0, 1y = 1, x0 = 1, and x1 = x. The first three of these special cases are handled by
<special cases 344>≡ if (iszero(x)) return AP_new(0); if (iszero(y)) return AP_new(1); if (isone(x)) return AP_new(< y is even 345> ? 1 : x->sign); <y is even 345>≡ (((y)->digits[0]&1) == 0)
The recursive case implements the fourth special case as well as the two cases described by the equation above:
<z ← xy 345>≡ if (isone(y)) z = AP_addi(x, 0); else { T y2 = AP_rshift(y, 1), t = AP_pow(x, y2, NULL); z = AP_mul(t, t); AP_free(&y2); AP_free(&t); if (!<y is even 345>) { z = AP_mul(x, t = z); AP_free(&t); } }
y is positive, so shifting it right one bit computes y/2. The intermediate results — y/2, xy/2, and (xy/2)(xy/2 — are deallocated to avoid creating unreachable storage.
When p is nonnull, AP_pow computes xy mod p. When p > 1, we can’t actually compute xy because it might be too big; for example, if x is 10 decimal digits and y is 200, xy has more digits than atoms in the universe; xy mod p, however, is a much smaller number. The following mathematical rule about modular multiplication can be used to avoid numbers that are too big:
( |
AP_mod and the static function mulmod collaborate to implement this rule. mulmod uses AP_mod and AP_mul to implement x·y mod p, taking care to deallocate the temporary product x·y.
<static functions 335>+≡
static T mulmod(T x, T y, T p) {
T z, xy = AP_mul(x, y);
z = AP_mod(xy, p);
AP_free(&xy);
return z;
}The AP_pow code when p is nonnull is nearly identical to the easier case when p is null, except that mulmod is called for the multiplications, p is passed to the recursive call to AP_pow, and x is reduced mod p when y is odd.
<z ← xy mod p 346>≡ if (isone(y)) z = AP_mod(x, p); else { T y2 = AP_rshift(y, 1), t = AP_pow(x, y2, p); z = mulmod(t, t, p); AP_free(&y2); AP_free(&t); if (!<y is even 345>) { z = mulmod(y2 = AP_mod(x, p), t = z, p); AP_free(&y2); AP_free(&t); } }
The outcome of comparing x and y depends on their signs and magnitudes. AP_cmp returns a value less than zero, equal to zero, or greater than zero when x<y, x = y, or x>y. When x and y have different signs, AP_cmp can simply return the sign of x; otherwise, it must compare their magnitudes:
<functions 335>+≡ int AP_cmp(T x, T y) { assert(x); assert(y); if (!<x and y have the same sign 338>) return x->sign; else if (x->sign == 1) return cmp(x, y); else return cmp(y, x); }
When x and y are positive, x <y if |x|<|y|, and so on. When x and y are negative, however, x<y if |x|>|y|, which is why the arguments are reversed in the second call to cmp. XP_cmp does the actual comparison, after cmp checks for operands of different lengths:
<static functions 335>+≡ static int cmp(T x, T y) { if (x->ndigits != y->ndigits) return x->ndigits - y->ndigits; else return XP_cmp(x->ndigits, x->digits, y->digits); } <prototypes 336>+≡ static int cmp(T x, T y);
The six convenience functions take an AP_T as their first argument and a signed long as their second. Each initializes a temporary AP_T by passing the long to set, then calls the more general operation. AP_addi illustrates this approach:
<functions 335>+≡ T AP_addi(T x, long int y) { <declare and initialize t 347> return AP_add(x, set(&t, y)); } <declare and initialize t 347>≡ unsigned char d[sizeof (unsigned long)]; struct T t; t.size = sizeof d; t.digits = d;
The second chunk above allocates the temporary AP_T and its associated digits array on the stack by declaring the appropriate locals. This is possible because the size of the digits array is bounded by the number of bytes in an unsigned long.
Four of the remaining convenience functions have the same pattern:
<functions>+≡ T AP_subi(T x, long int y) { <declare and initialize t 347> return AP_sub(x, set(&t, y)); } T AP_muli(T x, long int y) { <declare and initialize t 347> return AP_mul(x, set(&t, y)); } T AP_divi(T x, long int y) { <declare and initialize t 347> return AP_div(x, set(&t, y)); } int AP_cmpi(T x, long int y) { <declare and initialize t 347> return AP_cmp(x, set(&t, y)); }
AP_modi is the oddball, because it returns a long instead of an AP_T or int, and because it must discard the AP_T returned by AP_mod.
<functions 335>+≡ long int AP_modi(T x, long int y) { long int rem; T r; <declare and initialize t 347> r = AP_mod(x, set(&t, y)); rem = XP_toint(r->ndigits, r->digits); AP_free(&r); return rem; }
The two shift functions call their XP relatives to shift their operands. For AP_lshift, the result has ⌈s/8⌉ more digits than the operand and the same sign as the operand.
<functions 335>+≡
T AP_lshift(T x, int s) {
T z;
assert(x);
assert(s >= 0);
z = mk(x->ndigits + ((s+7)&~7)/8);
XP_lshift(z->size, z->digits, x->ndigits,
x->digits, s, 0);
z->sign = x->sign;
return normalize(z, z->size);
}For AP_rshift, the result has ⌊s/8⌋ fewer bytes, and it is possible that the result is zero, in which case its sign must be positive.
T AP_rshift(T x, int s) {
assert(x);
assert(s >= 0);
if (s >= 8*x->ndigits)
return AP_new(0);
else {
T z = mk(x->ndigits - s/8);
XP_rshift(z->size, z->digits, x->ndigits,
x->digits, s, 0);
normalize(z, z->size);
z->sign = iszero(z) ? 1 : x->sign;
return z;
}
}The if statement handles the case when s specifies a shift amount greater than or equal to the number of bits in x.
AP_toint(x) returns a long int with the same sign as x and with a magnitude equal to |x| mod (LONG_MAX+1).
<functions 335>+≡
long int AP_toint(T x) {
unsigned long u;
assert(x);
u = XP_toint(x->ndigits, x->digits)%(LONG_MAX + 1UL);
if (x->sign == -1)
return -(long)u;
else
return (long)u;
}The rest of the AP functions convert AP_Ts to strings and vice versa. AP_fromstr converts a string to an AP_T; it accepts a signed number with the following syntax.
number = { white } [ |
where white denotes a white-space character and digit is a digit character in the specified base, which must be from two to 36 inclusive. For bases that exceed 10, letters specify the digits that exceed nine. AP_fromstr calls XP_fromstr, and it stops scanning its string argument when it encounters an illegal character or the null character.
<functions 335>+≡ T AP_fromstr(const char *str, int base, char **end) { T z; const char *p = str; char *endp, sign = '�'; int carry; assert(p); assert(base >= 2 && base <= 36); while (*p && isspace(*p)) p++; if (*p == '-' || *p == '+') sign = *p++; <z ← 0 351> carry = XP_fromstr(z->size, z->digits, p, base, &endp); assert(carry == 0); normalize(z, z->size); if (endp == p) { endp = (char *)str; z = AP_new(0); } else z->sign = iszero(z) || sign != '-' ? 1 : -1; if (end) *end = (char *)endp; return z; }
AP_fromstr passes the address of endp to XP_fromstr because it needs to know what terminated the scan so it can check for illegal inputs. If end is nonnull, AP_fromstr sets *end to endp.
The number of bits in z is n·lg base where n is the number of digits in the string, and thus z’s XP_T must have a digits array of at least m = (n·lg base)/8 bytes. Suppose that base is 2k; then m = n·lg(2k)/8 = k·n/8. Thus, if we choose k so that 2k is the smallest power of two equal to or greater than base, z needs ⌈k·n/87⌉ digits. k is a conservative estimate of the number of bits each digit in base represents. For example, when base is 10, each digit carries lg 10 ≈ 3.32 bits, and k is four. k ranges from one, when base is two, to six, when base is 36.
<z ← 0 351>≡ { const char *start; int k, n = 0; for ( ; *p == '0' && p[1] == '0'; p++) ; start = p; for ( ; <*p is a digit in base 352>; p++) n++; for (k = 1; (1<<k) < base; k++) ; z = mk(((k*n + 7)&~7)/8); p = start; } <*p is a digit in base 352>≡ ( '0' <= *p && *p <= '9' && *p < '0' + base || 'a' <= *p && *p <= 'z' && *p < 'a' + base - 10 || 'A' <= *p && *p <= 'Z' && *p < 'A' + base - 10)
The first for loop in <z ← 0 351 > skips over leading zeros.
AP_tostr can use a similar trick to approximate the number of characters, n, needed for the string representation of x in base. The number of digits in x’s digits array is m = (n·lg base)/8. If we choose k so that 2k is the largest power of two less than or equal to base, then m = n·lg(2k)/8 = k·n/8, and n is ┌8.m/k┐, plus one for the terminating null character. Here, k underestimates the number of bits each digit in base represents so that n will be a conservative estimate of the number of digits required. For example, when base is 10, the digits in x each yield 8/lg 10 ≈ 2.41 decimal digits, and k is three, so space for ┌8/3┐ = 3 decimal digits is allocated for each digit in x. k ranges from five, when base is 36, to one, when base is two.
<size ← number of characters in str 352>≡
{
int k;
for (k = 5; (1<<k) > base; k--)
;
size = (8*x->ndigits)/k + 1 + 1;
if (x->sign == -1)
size++;
}AP_tostr lets XP_tostr compute the string representation of x:
<functions 335>+≡ char *AP_tostr(char *str, int size, int base, T x) { XP_T q; assert(x); assert(base >= 2 && base <= 36); assert(str == NULL || size > 1); if (str == NULL) { <size ← number of characters in str 352> str = ALLOC(size); } q = ALLOC(x->ndigits); memcpy(q, x->digits, x->ndigits); if (x->sign == -1) { str[0] = '-'; XP_tostr(str + 1, size - 1, base, x->ndigits, q); } else XP_tostr(str, size, base, x->ndigits, q); FREE(q); return str; }
The last AP function is AP_fmt, which is a Fmt-style conversion function for printing AP_Ts. It uses AP_tostr to format the value in decimal and calls Fmt_putd to emit it.
<functions 335>+≡
void AP_fmt(int code, va_list *app,
int put(int c, void *cl), void *cl,
unsigned char flags[], int width, int precision) {
T x;
char *buf;
assert(app && flags);
x = va_arg(*app, T);
assert(x);
buf = AP_tostr(NULL, 0, 10, x);
Fmt_putd(buf, strlen(buf), put, cl, flags,
width, precision);
FREE(buf);
}AP_Ts are similar to the “bignums” in some programming languages. Recent versions of Icon, for example, have only one integer type, but use arbitrary-precision arithmetic as necessary to represent the values computed. Programmers don’t need to distinguish between machine integers and arbitrary-precision integers.
Facilities for arbitrary-precision arithmetic are often provided as a standard library or package. LISP systems have long included bignum packages, for example, and there’s a similar package for ML.
Most symbolic arithmetic systems do arbitrary-precision arithmetic, because that’s their purpose. Mathematica (Wolfram 1988), for example, provides integers of arbitrary length and rationals in which the numerator and denominator are both arbitrary-length integers. Maple V (Char et al. 1992), another symbolic computation system, has similar facilities.
18.1 |
| ||
18.2 | The recursive algorithm used in z ← x, u ← 1 while y > 1 do if y is odd then u ← u·z z ← z2 y ← y/2 z ← u·z Iteration is usually faster than recursion, but the real advantage of this approach is that it allocates less space for intermediate values. Reimplement | ||
18.3 | Implement | ||
18.4 | The | ||
18.5 | Implement an | ||
18.6 | Design an interface whose functions do arithmetic modulo | ||
18.7 | Multiplying two
which takes four multiplications and one addition. The coefficient of the middle term can be rewritten as
The product xy thus requires only three multiplications (ac, bd, and (a−b)(d−c)), two subtractions, and two additions. When |