Chapter 12
FROM CATASTROPHE TO CHAOS: THE MODELING PRACTICES OF APPLIED TOPOLOGISTS
David Aubin
Sociologiquement, on peut dire que [la théorie des catastrophes] a fait… un naufrage subtil, parce que la plupart des notions que j'ai introduites … ont pénétré dans le bagage ordinaire des modélisateurs. Alors, il est vrai que, dans un sens, les ambitions de la théorie ont fait naufrage, ma is la pratique, elle, a réussi. [Thom, 1991, 47].
During World War II, American mathematician George D. Birkhoff contended that ‘topology deserves to obtain a more prominent position in physical theories than it has yet obtained’ [1943, 310]. Because of its impact on various parts of mathematics, topology undoubtedly was among the greatest successes of the twentieth century. But, prior to the early 1970s, and despite Birkhoffs wish, topology had generally retained the image of an abstruse pursuit that had found little concrete application elsewhere. Or to put it more accurately, very few leading topologists paid any attention to the concrete.1
By the early 1990s, a compelling alternative had emerged, and this image had become obsolete. For instance, British topologist E.C. Zeeman characterized the history of topology as a succession of hegemonic approaches branching off to establish new subspecialties. After the 1890s when it untangled itself from its ‘applied origins,’ topology was ‘analytic’ from 1900 to 1920, ‘geometric’ in the 1920s and 1930s, and then ‘algebraic’ But, the 1960s saw the resurgence of a ‘geometric’ standpoint, and the 1970s were labeled ‘differential.’ The wheel having turned a full circle, Zeeman saw in the 1980s the triumph of ‘applications.’2 Now, ‘applied topology’ is hard to find as a standard classification in mathematics. In more than fifty years, the Mathematical Review has recorded only one single use of the expression in the title of an article.3 Clearly, the image of topology seems to have shifted recently.
Although part of larger mutations in the image of mathematics, this shift is best understood as resulting from the successful adaptation of notions and practices coming from topology to the modeling of certain phenomena in the physical, life, and social sciences. This, I claim, was the result a systematic effort undertaken by those I will call ‘applied topologists.’ From the late 1950s onwards, they pursued vast programs, well adapted to the then dominant ideology of pure mathematics [Aubin, 1997]. Sometime in the 1960s, they turned their attention to the real world. Exploiting the newest mathematical technologies of their arsenal, they forged modeling practices capable of providing, or so they wished, theoretical explanations for phenomena badly understood by means of conventional approaches.4 But in so doing, they retained the Bourbakist ideal of exhibiting the deepest structures of the world.
Diversely known as the theories of catastrophes, dynamical systems, and deterministic chaos, these modeling practices benefited from the crucial catalytic role played by the Institut des hautes etudes scientifiques (IHES), at Bures-sur-Yvette near Paris [Aubin, 1998a; 1998b]. Hired there in 1963, French mathematician Rene Thorn welcomed notable visitors, such as E.C. Zeeman and the prodigious Berkeley mathematician Steve Smale. With students and followers, they forged a small community which promoted new methods for modeling, as well as the mathematical technologies needed for the task. However, following the media frenzy that greeted catastrophe theory, a backlash challenged the legitimacy of their approaches outside pure mathematics. No matter how ‘applied,’ topologists had trouble convincing communities of specialists of the fruitfulness of their methods. Was the world actually structured by topological concepts, or did they merely provide a language for grasping it? Applied topologists’ responses to skepticism varied greatly: Smale preferred to base his models on well-established mathematization processes; Zeeman tried to convince large audiences that catastrophe theory could actually be used to generate differential-equation models; and Thorn embarked on a grandiose enterprise intended to revolutionize the philosophy of science.
Ultimately, the success of some of the modeling practices promoted by applied topologists depended on the willingness of other specialists to claim them as their own. For this mediation, the IHES also provided a well-suited environment. Inspired by Thorn's and Smale's ideas, IHES physicist David Ruelle published, together with Dutch topologist Floris Takens, a seminal article in 1971, which in many ways launched the study of chaotic dynamics. An untypical physicist because of his emphasis on a mathematical rigor that bore Bourbaki's stamp, Ruelle served as mediator between applied topologists and physicists. This was by no means an obvious process. While topological modeling practices were widely picked up by specialists in various disciplines, this was done at the expense of substantial alterations and a loss of rigor. As a tradeoff, physicists exploited experiments and numerical simulations to bypass mathematical failures and philosophical pretense.
To make these modeling practices explicit, it has been necessary to select, as representative of particular variations, a few heterogeneous models, all of which constituted conscious and appealing attempts at extending the reach of topological tools and practices (Table 1). Not all of them, however, were promised a brilliant future; with the benefit of hindsight some might appear as rash acts of bravado soon to be harshly dismissed. By using these particular models as signposts, an overview of the evolution and diversification of topological modeling practices will be presented, and an important feature will be emphasized. This was the way topological approaches called into question the dominance of differential equations in modeling. In other words, they challenged the widespread assumption that theoretical accounts of natural phenomena were a matter of writing down, and if possible solving, the right equation. Topological technologies provided a language suited for a description of nature where differential equations were displaced in favor of much less important ontological commitments to fundamental laws.
This story therefore goes counter to the traditional historiography of ‘application’ in several ways: applied topologists’ construction of mathematical frameworks appears as being intimately intertwined with their forging modeling practices applicable to concrete problems; the role of mediators is emphasized; and the specialists’ successful ‘applications’ of topological practices are clearly seen as ‘adaptations’ betraying initial goals while offering original means of implementing abstract, philosophical undertakings. As a result, differential topology ceased to be just an abstract branch of mathematics to become a reservoir of tools and practices to be used in those cases when equations were hard to come by or solve.
THE ABSTRACT ROOTS OF APPLIED TOPOLOGY
Having been awarded their Ph.D.s in the 1950s, Rene Thorn and Steve Smale have both emphasized the special conditions in which they first approached topology. While the former modestly acknowledged that it was his luck to have joined the field just when ‘a river … flooded the domain,’ the later simply wrote that he ‘was born into the “Golden Age of Topology'” [Thorn, 1983, 21]; [Smale, 1990, 28]. A decade earlier,
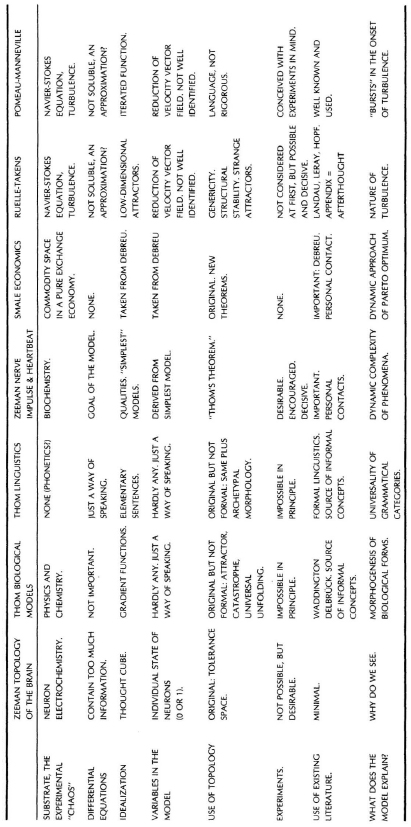
TABLE 1 SCHEMATIC REPRESENTATION OF FEATURES THAT BEST ENCAPSULATE OF THE MODELING PRACTICES EXHIBITED BY SEVEN TYPES OF TOPOLOGICAL MODELS, NAMELY, [ZEEMAN 1965; THOM 1969; THOM 1973; ZEEMAN 1973; SMALE 1973; RUELLE AND TAKENS 1971]; AND THE POMEAU-MANNEVILLE INTERMITTENT MODEL FOR THE ONSET OF TURBULENCE.
G.D. Birkhoff [1942J confidently suggested that topology would soon ‘greatly increase in scope and significance.’ Having witnessed ‘a kind of culmination in the abstract phase’ of the history of the field that had performed the ‘essential task of giving topological ideas their appropriate abstract setting,’ he believed that the future would show the usefulness of topology for dynamics.
The field indeed skyrocketed in the postwar years, but in a direction hardly anticipated by Birkhoff. Following MacLane and Eilenberg's 1945 axiomatization of homology theory, extraordinary technical developments in algebraic topology ignited an ‘explosion'—an internal explosion, but also an external one, extending the reach of topology ‘by the creation of methods applicable to new domains of the concrete’ [Lichnérowicz, 1955]. The main motor driving the explosion was the introduction of powerful algebraic tools for the study of topology and geometry. While vast fields of research opened up, extensions to concrete problems followed traditional patterns, application remaining outside the province of leading mathematicians. As put by Lichnérowicz, the next great ‘explosion’ took place in the direction of algebraic geometry: ‘I dare say it was detopologized and partly transmuted into a purely abstract geometry.’ Still, the systematic algebraic attack by the new generation was resented by some old-guard mathematicians who contended that ‘while we wrote algebraic GEOMETRY they make it ALGEBRAIC geometry with all that it implies’ [Lefschetz, 1986, 3]. Similarly, Marston Morse criticized algebraic supremacy and disdain for applications: ‘Forever the foundations and never the Cathedral’ [quoted in Bott, 1980, 908].
For those who would become applied topologists, these older traditions (found in the work of Whitney, Morse, and later Lefschetz, Birkhoff, and Poincaré) provided resources to complement the algebraic dominance. But, in the context in which they produced their first results, Smale, Zeeman, and Thorn approached topological problems from purely internal motives, without paying attention to applications. In so doing, they achieved great successes acknowledged by their peers. In 1960, Smale proved the higher-dimensional Poincaré conjecture to which Zeeman contributed a different proof: for this the former was awarded a Fields Medal in 1966. Earlier, in 1958, Thorn had already received the Medal for his work on cobordism. However, albeit educated by Bourbaki mathematicians, Thorn, like Smale and Zeeman for that matter, tackled topological problems from a geometric, more than algebraic, standpoint. When topology was in a ‘stage of vigorous … algebraicization,’ Heinz Hopf wrote when presenting Thorn his Medal, lurked the danger of ‘totally ignoring the geometrical content of topological problems.’
In regard to this danger, I find that Thorn's accomplishments have something that is extraordinarily encouraging and pleasing. While Thom masters and naturally uses modern mathematical methods and while he sees the algebraic side of his problems, his fundamental ideas … are of a perfectly geometúc-anscbaulicb nature [Hopf 1960, lxiii-lxiv].
By the late 1950s, Thom and Smale were moving away from their earlier concerns and embarking on ambitious programs. Reviving interest in topological notions such as genericity and structural stability, they endeavored to construct global classification schemes for familiar entities: real functions and differential equations, respectively. At the end of decade, Thorn's project had partly been completed with the list of the seven elementary catastrophes [Thom, 1975], while Smale's, despite bold conjectures and great advances, was facing grave difficulties [Smale, 1969/70]. As a result of constant interactions, however, both were then definitively turning away from abstract pursuits and engaging in problems of modeling.5
THE EMERGENCE OF ‘TOPOLOGICAL MODELS’
In 1969, Rene Thom proposed noteworthy ‘topological models,’ with photographs of caustics and plaster models, in the journal Topology. Concerned with the problem of explaining ‘the stability … of the global spatio-temporal structure in terms of the organization of the structure itself,’ he thought of his models in terms of a ‘striking analogy between this fundamental problem of theoretical Biology and the main problem considered by the mathematical theory of Topology, which is to reconstruct a global form … out of all its local properties’ [Thom, 1969, 313]. For him, it was not only the tools of topology which could be applied to biology, but the very nature of both endeavors which suggested that involved interactions could be productive for both disciplines.
Obviously, this dramatic extension of the meaning of model is but a small part of the larger story of mathematical modeling, which to a large extent remains to be told by historians of science.6 The idea came to Thom from his encounter with an original topologist, Christopher Zeeman, who had already spoken of topological models in an article by which Thorn had been ‘singularly fascinated.’ According to von Neumann, ‘the sciences do not try to explain, they hardly even try to interpret, they mainly make models’ [quoted in Dahan Dalmedico, 1996, 179]. Contrary to this pragmatism, Thorn and Zeeman believed their models to be more than descriptions or computational techniques, but forms of explanation.
Topology of the Brain: The Irrelevance of Differential Equations
The intelligibility of the experimental ‘chaos’ depended on mathematics’ very ‘power to simplify and explain,’ Zeeman [1964a] claimed in accordance with the credo of a mathematician raised in Bourbaki's heydays. More than any other topologist of his time, however, he seriously worked out models, in particular ‘to try and explain the relationship between mind and brain’ [Zeeman, 1965, 277]. His principal goal was to provide explanations for such problems as: How does the brain perceive an image from nervous impulses? To tackle this question Zeeman used algebraic topology, because it was 'well adapted to ignore local variations and capture global properties'' [277]. In biophysics, one usually started with electrochemical properties expressed as measurable quantities, then one derived and if possible solved differential equations which they obeyed. But, as Zeeman explained, models built with such equations ‘frequently give the impression of being too detailed neurologically and oversimplified in the large.’
To pursue an analogy, think of blowing up a balloon into a funny shape. The local behaviour of the rubber material is described accurately by differential equations, but globally the equations become either very complicated or else inadequate, whilst the topology remains very simple [287].
Granted that mind mechanisms relied on interactions of neurons, algebraic topology, like a net catching global, relevant features in a sea of local, irrelevant complexity, provided original tools enhancing the understanding of the workings of the brain.
Zeeman introduced ‘a simple model of the brain’ by organizing neurons into a cube of 10 billion dimensions called ‘the thought cube.’ To work with such a complicated construct, topological techniques were called to the rescue. He devised the notion of tolerance spaces, accounting for pairs of distinct ‘states of neural activity … so close that they “feel the same” and consequently give rise to the “same thought”’ [282]. Modeling the brain, he was led to original and ‘precise’ mathematics.
Some features however made Zeeman's model unattractive to biologists. Even if he claimed that it was ‘based on the well known anatomical structure of the brain,’ his model was too crude for them [291–2]. It was moreover difficult to test in the laboratory.
The results are expressed in geometrical language, and are qualitative rather than quantitative. This means that so far the theory … has attempted to explain phenomena rather than predict the measurements that experiment would obtain [277].
As is well known, while Thorn mathematically defined catastrophes, Zeeman introduced the catchy phrase of catastrophe theory.7 Extending its range, he audaciously developed scores of famous (and infamous) models [Zeeman, 1977]. Far from resulting from his mere reading of an ‘underground’ copy of Thorn's manuscript, Zeeman's interest stemmed from constant contacts between the two men, thanks to which emerged a modeling practice that topologists could call their own.
By the same token, exploiting topological tools to make sense of the brain without paying attention to biochemical processes, Zeeman invented modeling procedures exhibiting many of the features which became trademarks of catastrophe theory. In his model, the substrate (the neurons) was replaced by an idealization with crude dynamics: the thought cube. The model variables were more or less realistic, and differential equations deemed uninteresting because containing more local information than needed. Topological technologies could filter out irrelevant information in favor of meaningful wholes. Experimental confirmation would be difficult, but perhaps not impossible; the goal of modeling was to explain rather than to predict. These features, which would all explicitly or implicitly inform later attempts at forging topological modeling practices, were more systematically expounded by Thorn.
Topological Models in Biology: Dynamics without Equations
From 1966 onward, Thorn publicly embarked on the ambitious adventure of catastrophe theory. Although mentioning ‘topological models,’ he casually used the term to refer to abstract mathematical constructs. He distinguished two kinds of models. On the one hand, he called differential models those given by a dynamical system: dxi/dt = Xi(x,τ,t), where τ represented external parameters. Classic and common, these models suffered from two well-known problems: X was rarely obvious to find especially in the nonphysical sciences, and solutions were often impossible to compute formally.
On the other hand, Thorn defined a new type of mathematical model. Inspired by British embryologist C.H. Waddington, he provided a mathematical definition for his informal notion of chreods, or stable pathways of development. For Thorn, an ‘experimental morphology’ defined a ‘catastrophe set’ of discontinuities dividing the substrate into regions controlled by chreods. This decomposition, he wrote, could ‘be considered as a kind of generalized m-dimensional language: I propose to call it a “semantic model”.’ He identified two kinds of problems to be considered given such a model:
1) To classify all types of chreods, and to understand the nature of the dynamic processes which insure their stability.
2) …Generally, there are some associations of chreods which appear more frequently than others. One may speak, in that case, of a multi-dimensional syntax directing the semantic model. The problem is then to describe this syntax [Thorn, 1969, 321–322].
Like Zeeman's, these were problems well suited for topology. Thorn referred to Poincaré's qualitative dynamics, and more crucially to Andronov and Pontrjagin's notion of structural stability. Recent developments due to Smale [1967] having weakened its usefulness, Thom defined attractors and restricted his study to systems which had a finite set of structurally stable attractors. The decomposition of the substrate in basins of attractors characterized ‘entirely the dynamical behaviour of the system.’ Thus were topological tools brought to bear on the ‘semantic’ problems raised by Thom. ‘In such a model, the fundamental phenomenon to be studied is the destruction of a structurally stable attractor by variation of the vector field’ [Thom, 1969, 323]. To use the tools of topological dynamics, he assumed that, like for traditional models, natural processes were described by vector fields. Inspired by Andronov, Thom allowed the equation to vary, and instead of studying solutions, he focused on global topological features. But, contrary to Andronov, the ultimate validity of idealized differential equations was irrelevant to Thorn's concerns.8
Thorn's models were no more amenable to experimental control than Zeeman's. His method merely provided an ‘art of models.’ Faced with the ‘need … to classify the [empirical] data,’ modelers could use his proposals as a substitute to ‘pure chance and lucky guess’ and achieve ‘a qualitative understanding of the process studied.’9 However, the most important consequence of Thorn's proposals lay not in his strenuous efforts at constructing a philosophy of science, but rather in the introduction of modeling practices taken up by some topologists, as the following examination of three models shows.
APPLIED TOPOLOGY? MODELING PRACTICES AT BAHIA, 1971
In 1971, the University of Bahia, Brazil, held a symposium on dynamical systems that provided an occasion for applied topologists to proclaim vocally that one could put ‘under the sway of the mathematician a vast array of phenomena thus far considered beyond his reach’ [Peixoto, 1973, xiii]. Although most participants dealt with pure mathematics, Smale, Thorn, and Zeeman presented models based on differential topology. Thorn's article aimed at providing a geometric interpretation of language and its grammatical categories. In his paper, Zeeman intended to ‘abstract the main dynamical qualities of the heartbeat and nerve impulse, and then build the simplest mathematical model with these qualities.’ By far the most mathematically involved, Smale's contribution attempted to put time back into the equations of equilibrium economics. A comparison of these three articles makes points of convergence and divergence appear explicitly.
The Bahia Models: Topological Modeling at Work
Of the three, Thorn's [1973] article was the most verbose. Were it not for its mathematical metaphors, it would have seemed closer to a philosophical paper. As it is difficult to consider this paper as an actual attempt at mathematical modeling, its legacy still being a matter of important dispute, it will not be discussed in detail. However, one should note that, while often claiming that his practice was independent of the substrate, Thorn made clear that it was rather without substrate. In his purely topological modeling, no variable nor equation was involved. In the absence of precise substrata lay the most extreme difference between Thorn's practice and that of other applied topologists.
Catastrophe Theory à la Zeeman: Deriving Equations from Topology
A perfect exemplar of the modeling practice most often associated with catastrophe theory, Zeeman's Bahia paper was an expose of the way in which this theory provided ‘not only a better conceptual understanding, … but also explicit equations for testing experimentally.’ He took seriously the idea that global analysis modeled qualities. For the heartbeat and nerve impulse, he contended, three main dynamical qualities were displayed: ‘(I) stable equilibrium; (II) threshold, for triggering an action; (III) return to equilibrium’ [Zeeman, 1973, 684]. Clearly, these were not simple physiological descriptions, but idealizations of biochemical processes, crucially informed by the types of behavior best suited for qualitative dynamics. Equilibrium meant ‘look for attractors', and threshold that a catastrophe was involved. Starting from the three qualities, Zeeman derived the simplest mathematical model displaying such features:
where dots denoted derivation with respect to time [699].
At this point catastrophe theory explicitly entered Zeeman's modeling practice. Using general arguments for deriving his ‘simplest’ model, he needed ‘Thorn's deep uniqueness theorem’ to argue that these models were indeed the right ones. ‘Let us pause for a moment to consider what we are doing,’ Zeeman wrote:
The topologist regards polynomials as rather special, and tends to turn his nose up at so crude a criterion of simplicity … So perhaps we ought to consider all possible surfaces [models]. Now comes the truly astonishing fact: when we do consider all surfaces, not only is this particular surface the simplest example, but in a certain sense it is … the unique example. Herein lies the punch of the deep and beautiful catastrophe theory [704].
A common strategy among applied topologists consisted in substituting mathematical justifications for metaphysical assumptions, namely in this case, the postulate of simplicity.10 As Zeeman interpreted it, Thorn's theorem implied that if the dynamics were postulated to depend on a generic potential, then the simplest model represented ‘the most complicated thing that could happen locally … The theorem is the key mathematical fact behind our whole approach’ [706]. His actual use of topology was therefore limited but crucial.
Next, by confronting his model with observations, experiments, and empirical models, Zeeman wished to interpret its variables in terms of physical parameters, but very loosely: one variable, for example, being identified as ‘chemical control… possibly membrane potential’ [712–3]. In striking contrast to his previous attitude when modeling the brain, differential equations remained the goal of Zeeman's modeling practice, using topological qualities to get them, rather than observations of empirical quantities. Using radical means to derive applied mathematicians’ classical objects, he laid himself open to the harshest critiques [esp. Zahler and Sussmann 1977].
Topologizing the Mathematical: The Case of Economics
Before his 1970 visit to the IHÉS, Steve Smale had scarcely dared to publish articles devoted to mathematical modeling. Inspired by Thorn, and wondering ‘whether I should explicitly direct my work toward socially-positive goals,’ he turned to applications [Smale, 1972, 3]. At Bahia, albeit providing economic justifications, he nevertheless expressed his problem in uncompromising mathematical terms:
One is given real differentiable functions ui: W → R defined on a manifold W, say i = 1, …, m. What is the nature of curves φ: R → W with the derivative (d/dt)(uioφ)(t) positive for all i, t [Smale, 1973, 532].
Contrary to Thom and Zeeman, Smale chose to rely on a rigorous, axiomatized treatment—provided by [Debreu, 1959]—of the domain he was dealing with. Entering a field already using sophisticated mathematical techniques, which he translated into a topological framework, he was making them ‘attractive to the modern mathematician, … brought up in the purist, Bourbakist style of education’ [Smale, 1980, 100]. Economics provided him with interesting mathematical problems where he could use dynamical systems theory. Thus, as opposed to Thom and Zeeman who did not prove anything, the main body of Smale's paper was a list of theorems proved for the sake of pure mathematics. Building on an already well-mathematized discipline and not turning his back on the specialists’ previous work, Smale promoted modeling practices that could be more easily adapted to established practices.11
Since Smale made no actual attempt at building economic models, his Bahia article provides a poor example of his modeling practice. Like Thom and Zeeman, however, he saw in topology a reservoir of techniques for the modeling of phenomena in biology, mechanics, electronics, etc. Abstracting topological features from known models, his modeling practice consisted in topologizing extent models and accounting for their dynamic behavior. This led him to specify assumptions hidden in models, understand some of their consequences, and modify hypotheses when needed. Later, Smale promptly recognized the importance of the Ruelle-Takens model, and crucially mediated between mathematicians and physicists.
A New Status for Differential Equations?
'In a large number of cases, a kinship of structures in extremely diverse domains has been noticed. This allows today's mathematician, without becoming an expert in a branch that is not the object of his study, to understand its essential [features].’ In 1968, this was how director Leon Motchane explained the fruitfulness with which many mathematicians orbiting the IHÉS were tackling concrete problems. Their effort was systematic and concerted. Designed to promote the advancement of ‘fundamental research’ but sponsored by industry, the Institut of Bures-sur-Yvette provided a fertile ground for the development of topological modeling practices. Beyond applied topologists’ personal motives, one must note how well this undertaking fitted with the ideology of research promoted by Motchane. Indeed, by insisting on the independence of research while emphasizing potential concrete benefits for industry, he favored abstract frameworks which paid attention to the outside world. Vehemently autonomous with respect to traditional practices in the sciences, applied topologists developed models intended as intelligible explanations rather than computing procedures for action [Aubin, 1998b]. By contingency, the IHÉS provided an impulse and some of the means for the emergence of a community of mathematicians willing to adapt their practice to the concrete. By 1971, the most eminent among them, Smale, Thom, and Zeeman each believed that, armed with their topological background, they could build dynamical models for all sorts of sciences, while keeping them at arm's length. Dynamics however had an unusual sense: it emphasized changes, but not forces responsible for change.
Clearly, it was not a unified modeling practice that emerged from applied topologists’ work. Their respective attitudes differed markedly with respect to the sciences they intruded, with respect to extant models, experimental results, or literature. At first glance, the most important difference concerned the goal of modeling and the place they assigned to differential equations. As mentioned, a most striking aspect of Zeeman's modeling practice lay in the Copernican reversal he advocated. Instead of looking for equations obeyed by observable variables, he derived them through topological considerations; only as a second step did he identify his variables with observations. Still, the derivation of equations remained the goal of his practice. On the contrary, Thorn's and Smale's papers made little use of substrata, variables, or equations. Consequently, by proposing mathematical descriptions in the absence of equations, the latter two opposed more drastically traditional practices than the former who merely proposed new means to achieve standard objectives.
To emphasize this opposition too strongly nonetheless is deceptive, since all shared a belief that topology served to constrain possible representations of phenomena. For Thorn, more than a mere reservoir of metaphors, mathematics provided a way of thinking. For Smale, the mathematician proved theorems which disturbed the established consensus. Of course, Zeeman was the most explicit in expressing this belief, attracting the obvious criticism that he let mathematics dictate what reality should be like. As a consequence of this shared belief, applied topologists challenged the traditional role ascribed to differential equations in modeling. Although a dynamical substrate in terms of vector fields was always assumed, they paid little attention to usual ways of deriving equations. While Zeeman's Bahia models proposed new ways of achieving standard goals, other models, including his own of the brain, suggested methods not only to analyze global features without solving equations, but more importantly to provide explanations of phenomena when underlying dynamical equations were not precisely known. This last suggestion would be widely taken up by physicists.
TOPOLOG1CAL PHYSICS? MODELING PRACTICES OF CHAOS
Remarkably, applied topologists’ efforts, which if restricted to them only might have remained rather sterile, were expanded upon by some physicists. In this process, the IHES served as a crucial mediator. Its physics section had always been characterized by a focus on rigor, and some noticeable instances of interactions with mathematicians had already taken place [Zeeman, 1964b]; [Froissart, 1966]. That Ruelle and Takens's theory of turbulence relied on concepts introduced by Smale and Thorn is clear simply by looking at their joint paper. But Ruelle's modeling practice also was shaped by his situation at the IHES, which was not only an opportunity for him to learn about recent theories, but showed him how to exploit them for model-building, as a comparison with the Bahia models will make clear.
Ruelle-Takens: A New Definition for Turbulence
Russian physicist Lev Landau [1944] and German mathematician Eberhard Hopf [1942; 1948] contended that when a fluid was submitted to increasing external stress, it went through a series of bifurcations, where appearing frequencies gave rise to quasiperiodic motions that seemed increasingly turbulent. Being in contact with applied topologists, Ruelle and Takens suggested, but did not show rigorously, that this bifurcation sequence stopped after the manifestation of three different modes because a ‘strange attractor’ appeared in a ‘generic’ manner. As the title of their paper indicated, what was at stake was the very nature of turbulence. Aperiodic—not quasiperiodic— motion was the definition they offered for it.
There was a striking feature in Ruelle and Takens's article which brought out the new status they assigned to differential equations. Indeed, they did not feel the need to write down the Navier-Stokes equations (NSE), the fundamental law for fluid flows, more explicitly than:
‘For our present purposes,’ they added, ‘it is not necessary to specify further … Xμ' [Ruelle and Takens, 1971, 168]. A unique parameter depending on physical characteristics, μ represented external stress on the fluid (e.g. the Reynolds or Rayleigh number). The determination of critical values at which motion became turbulent had motivated studies for almost a century [Aubin, 1998a]. Not interested in particular critical values, Ruelle and Takens only looked at general features of motion as the parameter increased.
When μ = 0, the fluid tended to rest; for small μ, it tended toward a stationary motion in which the velocity field remained constant. At a critical value μi, the system went though a Hopf bifurcation: the velocity field started to oscillate at a given frequency u>i. In phase space, while for stationary flows a fixed point existed which was an attractor of the system, when the oscillatory mode appeared this point exploded into a closed curve. At a further critical value μz, a second bifurcation gave rise to a frequency u>i, and so on. When μ increased sufficiently, ‘the fluid motion becomes very complicated, irregular and chaotic, we have turbulence’ [Ruelle and Takens, 1971, 168]. But how to describe this ‘chaotic’ flow? Based on their topological knowledge, Ruelle and Takens claimed that since the quasiperiodic motion was not generic for general dissipative systems, it had no chance of being observed. One had to look elsewhere for a ‘mathematical explanation’ of turbulence [Ruelle, 1972].
Topology in the Ruelle-Takens Model
Compared to the Bahia models, Ruelle and Takens's was closest to Smale's. Since fluid mechanics is one of the oldest mathematized disciplines, this might have been expected. Given by the velocity field of fluid flows and NSE, Ruelle and Takens's substrate was quite uncontroversial. But as in the above, identification of model variables with observable ones was not immediate, for the phase space of the velocity field was infinite-dimensional, a problem as far as dynamical systems theory was concerned. Thus, while the substratum was straightforward, the pertinence of reducing it to a low-dimensional manifold was not obvious.
When, using an example of Smale's (the famous horseshoe), they defined strange attractors and argued for their genericity, Ruelle and Takens made one crucial conceptual innovation in dynamical systems theory. But more importantly, they adapted a crucial part of applied topologists’ modeling practices. Revived by Thorn, the notion of genericity was the core of applied topologists’ work both in mathematics and modeling. Still, Thorn [1975, 35] was aware of its slipperiness, and Smale [1967, 748] made a welcome clarification when he restricted its use to properties of topological spaces rather than points. The use of genericity remained an art difficult to make rigorous. One of the weakest in Zeeman's use of catastrophe theory for modeling, this point remained a tricky matter for physicists, as we shall see.
Noting that Smale's horseshoe was stable under small perturbations, Ruelle and Takens concluded that ‘the existence of such a “strange” attractor therefore is not a non-generic pathology’ [Ruelle and Takens, 1971, 171]. By indicating that in the neighborhood of quasiperiodic motions in more than 3 dimensions a generic set of such attractors should exist, they felt entitled to pronounce that quasiperiodic motions could not physically occur. But one should note the tentativeness of their language:
For μ. > 0 we know very little about the vector field Xμ. Therefore it is reasonable to study generic deformations from the situation at μ = 0. In other words we shall ignore possibilities of deformations which are in some sense exceptional … It appears … that a three-dimensional viscous fluid conforms to the pattern of generic behavior which we discuss [Ruelle and Takens, 1971, 168, my emphasis].
By adapting topological modeling practices to the turbulence problem, Ruelle and Takens were in a situation similar to Smale's. A huge literature could be tapped into in order to argue for the plausibility of their model, but this had to be done in a new framework, which, in traditional views, still lacked a solid mathematical basis. Significantly, most references to this literature were included in an appendix written later and a note published in a following volume of the journal. Ruelle and Takens had come up with their model while trying to adapt topological practices to the turbulence problem, but still tried to root it in a mathematized tradition. More significantly still, the process by which their paper became a seminal one was hardly straightforward. The resistance they encountered was overcome only after specialists in the mathematical study of fluid dynamics could incorporate topological practices into their analytical framework, and after experimental results indicated that the Ruelle-Takens model accounted for observation more accurately than Hopf's and Landau's.
Topological Modeling by Physicists: The Example of Intermittence
Ruelle and Takens's proposal revolutionized the way theoretical physicists could deal with differential equations. This alternative modeling practice displaced earlier emphases put on specific models of nature in order to tackle classes of models. That they made no use of the specific form of NSE was symptomatic. A hydrodynamicist later wrote that this was ‘a point of philosophy:’ without arguing about the relevance of NSE, ‘I ought to confess we can forget about them here’ [Velarde, 1981, 210]. Without resolving the conundrum of the relationship between fundamental laws and observation, this practice made models cheap and dispensable, and focused rather on essential topological features of observed behaviors assimilated to structural, yet dynamical, characteristics of classes of models. In short, physicists were now allowed to stop looking for specific representations of nature, and acquired means of studying the consequences of the mode of representation itself.
Characteristic of applied topologists’ modeling practices, this approach would exert an important appeal in the following decade. In the last section of this chapter, the discussion of another model for the onset of turbulence will underscore the fact that the extension of topological modeling practices to physics was done at the expense of the rigor that applied topologists wished to retain and in interaction with the results of experimentation and simulation. The model selected for discussion is known as the Pomeau-Manneville scenario. Developed in the late 1970s, it is representative of the tradeoffs accompanying the adaption of topological modeling practices to physics and other mathematized disciplines.
One of the rare theoretical physicists who paid early attention to the Ruelle-Takens model, Yves Pomeau, from the French Commissariat à l'énergie atomique (CEA), had arrived, by 1976, at a coherent picture of chaotic behavior. Inspired by Thorn, Smale, and Ruelle, he adopted a highly mathematical language. But, Pomeau understood that merely to propose ‘revolutionary’ models was not enough. One needed to get one's hands dirty, compare theory with experiment, collaborate with people from previously separate disciplines, and forge a common language. In 1976, two CEA experimental physicists, Pierre Bergé and Monique Dubois had built a Rayleigh-Bénard system—a cellular cavity filled with fluid where a gradient of temperature induced convection. A singular phenomenon caught their attention: ‘the velocity amplitude shows intermittent periodic oscillations versus time’ [Bergé and Dubois, 1976]. Studying a computer model, Pomeau noticed similar intermittent flashes. Together with Paul Manneville, a young CEA theoretician, they came up with a series of bifurcations, different from the Ruelle-Takens scheme, leading to the onset of turbulence.
Pomeau and his collaborators faced similar data on systems that a priori had little to do with one another: time series exhibiting regular periodic behavior randomly and abruptly disrupted by erratic bursts. In trying to find a common cause for these behaviors, a dynamical systems approach proved useful. Disputing the claim that the Ruelle-Takens model was the only way to turbulence, they contended: ‘theories based on genericity arguments [are] sufficiently versatile to allow for different possible transitions’ [Bergé & al., 1980, L341]. They considered a Poincaré map of a dynamical model yn+1 = f(yn, r), where for the control parameter r slightly below a critical value rT, the curve f had two intersection points with the diagonal, while ‘for r > rT the curve is lifted up and no longer crosses the [diagonal] so that a “channel” appears between them’ (Fig. 1) [Pomeau and Manneville, 1980, 190]. This simple picture, they contended, was ‘displaying generic features susceptible of explaining the experimental observations’ [Bergé & al., 1980, L343]. When the system passed through the channel, its behavior seemed regular. Leaving the channel, it explored chaotically other regions of phase space until it was again trapped into such a channel.
Pomeau and Manneville's modeling practice lay in between that of applied topologists and the traditional practice of physicists based on explicit dynamical systems. Like applied topologists, they started with
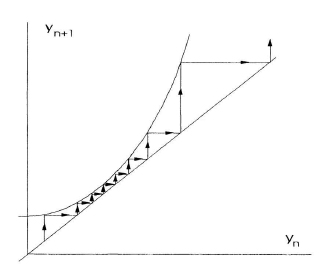
FIGURE 1 POINCARÉ MAP FROM THE LORENZ MODEL, WITH THE PARAMETER r SLIGHTLY ABOVE THE CRITICAL TURBULENT VALUE rT. CORRESPONDING TO THE REGULAR FLUID MOTION, THE SLOW DRIFT THROUGH THE CHANNEL IS QUITE IMPERCEPTIBLE ON EXPERIMENTAL OR NUMERICAL TIME RECORDS. REDRAWN FROM [POMEAU AND MANNEVILLE 1980, FIG. 4]
features to be explained topologically, rather than by relying on precise differential equations; bifurcations again were interpreted as sources for change. Like them, they assumed that an ‘unknown realistic dynamical system’ existed, which ‘should share some generic properties with already well studied models’ [Bergé &c ah, 1980, L342]. Properties of other systems provided an explanation for experimental behaviors stemming from a similar, but unknown, equation. Unlike applied topologists, however, they neglected to ground their model in rigorous mathematics. ‘The reader must be warned that the discussion is made in physical terms. No proof is given’ [Pomeau and Manneville, 1979, 331]. Their use of genericity arguments was especially loose. For them, a generic property was simply one often encountered when varying parameters in numerical simulations or laboratory experiments.
In their footsteps, Jean-Pierre Eckmann, from Geneva, reviewed the physicist's attitude with regard to topological methods, which constituted a language for describing deterministic evolution equations.’12 Although a rigorous classification was far from achieved, experiments could guide physicists to relevant bifurcations. Topology did not constrain reality. On the contrary, reality prescribed the topological notions that could be usefully mobilized for the understanding of phenomena. While Ruelle and Takens had argued that topological considerations alone implied that the onset of turbulence was due to the stability of strange attractors, the physicists countered that many ‘scenarios’ could take place. All that Eckmann could say was ‘if certain things happen as the parameter is varied, then certain other things are likely to happen as the parameter is varied further.’ Linked with genericity, the definition of likely, ‘in a physical context,’ was tricky.
I do not intend to go to any philosophical depth but, rather, take a pragmatic stand. (1) One never knows exactly which equation … is relevant for the description of the system. (2) When an experiment is repeated, the equation may have slightly changed … (3) The equation under investigation is one among several, all of which are very close to each other [Eckmann, 1981, 646].
Inspired by Thorn and Ruelle, this type of mathematization was ‘answering new types of questions which are more or less independent of detailed knowledge of the dynamics of any given physical system’ [Collet & al., 1981, 1]. Its validity therefore did not depend on fundamental laws. Out of a mathematical failure, a modeling practice was built by physicists for physicists. While mathematicians had not succeeded in classifying generic bifurcations, Eckmann's scheme provided an experiment-based topology of dynamical systems.
CONCLUSION
In 1977, in the midst of raging controversies, Rene Thorn granted that catastrophe ‘theory could have the same fate as cybernetics or information theory … a considerable sociological craze, which short of effective success ends up by falling on the distaff side’ [Thorn, 1977a, 681]. And to a large extent it did. To explain the strong rejection he encountered, Thorn mustered sociological arguments. ‘It was a corporate reaction: the whole community of applied mathematicians rose up against the theory’ [Thorn 1992, 45]. He went as far as suggesting that ‘the interests of the computer industry [were] perhaps not entirely foreign to this affair’ [Thorn, 1977b, 196]. Fundamentally devoted to computation, they just had to oppose an essentially qualitative enterprise! It is not uncommon for scientists to ascribe the rejection of endeared theories to social factors. But, if we accept Thorn's interpretation, how are we to account for the fact that, although sharing many practical features with catastrophe theory, the qualitative study of chaotic systems was rather welcomed by applied mathematicians and the computer industry alike?
In fact, Thorn perceptively hinted at the different ways in which topological modeling could be put to use when he suggested that catastrophe theory followed a ‘twofold way.’
Either, starting from known scientific quantitative laws, … you insert the CT formalism; … this is the ‘physical’ way. Or, starting from a poorly understood experimental morphology, one postulates ‘a priori’ the validity of CT formalism, and one tries to reconstruct the underlying dynamics which generates this morphology: this is the ‘metaphysical’ way [Thom, 1976, 235].
Ridiculed by critics, this alternative amounted, in their view, to a choice between triviality and arbitrariness, if not nonsense. Using Thorn's dichotomy, the models discussed above can be seen as treading the ‘metaphysical’ way in Thorn's and Zeeman's cases, and following the ‘physical’ way for the others. The Ruelle-Takens model aptly showed that this latter way by no means implied triviality. Topological modeling practices provided means to account for behaviors without solving equations and could even be exploited to exhibit hitherto unsuspected phenomena.
As suggested by the case of fluid mechanics, corporate reactions were not directed against the goal of the modeling defended by applied topologists, so much as against its means. Even if especially exciting because they allowed new kinds of questions to be tackled, topological tools, people objected, had no right to constrain reality, at least for as long as the general mathematical framework was not completely proved rigorously, something that was not likely to happen quickly. Specialists opposed the perception that models could be built while neglecting established traditions, literature, experimental and numerical results, etc. But they acknowledged that tools coming out of applied topologists’ work provided bases for a new hybrid language useful in the description—not the constriction—of reality.
By discussing the modeling practices of applied topologists and their adaptation by physicists, this chapter has demonstrated remarkable shifts in the practice of some topologists who imagined that they could extend their skills to the world of models, and in that of some physicists who started to adapt concepts and practices of this heretofore abstruse branch of mathematics, topology. In this process, of course, images were not left untouched. But was the reverse also true? How did global shifts in images of mathematics also contribute to the emergence of alternative practices for topologists and physicists alike? The puzzling issues raised by Dahan Dalmedico [1996J about the hegemony of pure mathematics in 1945–70, and the subsequent feeling that, after decades of Bourbakism, mathematics went back to the concrete [Houzel, 1979], are nicely illustrated by the story of applied topologists. Other case studies are needed to complete the picture.
ACKNOWLEDGMENTS
This paper has benefited from the guidance of M.N. Wise, A. Dahan Dalmedico, and M.S. Mahoney. I thank IHES and the College de France for allowing me to use their archives. It is a pleasure to acknowledge the kindness with which V.I. Arnol'd, P. Bergé, M. Dubois, J.P. Eckmann, P. Manneville, Y. Pomeau, M. Peixoto, D. Ruelle, and R. Thorn answered my questions either personally or in writing. This work was supported by the Social Science and Humanities Research Council (SSHRC) of Canada and the American Philosophical Society.
NOTES
1. Classic histories of topology bear a strong Bourbakist stamp [Dieudonné 1989; 1994; Pont 1974]. Recent studies, devoted to earlier periods, have however tended to dispute the internalist view; see e.g. [Epple 1998; and Feffer 1997].
2. The transparencies of Zeeman's lecture delivered on October 27, 1993 at Berkeley, are reproduced on the World Wide Web: http://www.math.utsa.edu/ecz/l_ht.htm. By no means was he alone in seeing the traditional image of topology as having been radically challenged; see e.g., [Browder 1989; Jaffe and Quinn 1993–1994; Atiyah 1995],
3. [Henderson and Maunders 1969], Reviewing a paper on ‘Hilbert's Sixteenth Problem,’ by George Wilson {Topology, 17 [1978]: 53–73), H.B. Griffiths also used the expression (with quotation marks). Cf. Mathematical Review, item 58#16684.
4. By modeling practice, I mean the actual activities in which scientists engage when they build models. They include tacit sets of assumptions, mathematical technologies, and frameworks for inrerpreting results; see [Aubin 1998a]. On ‘theoretical technologies,’ which include concepts, tools, and practice, see [Warwick 1992].
5. Applied topologists were sensitive to changes in the social and political status of mathematics. Growing demands for utility and concerns for the political responsibility of mathematicians were among the factors that directed theit attention to issues of modeling [Aubin 1998a]. In addition, economic conditions may also have been involved, although as far as 1 was able to determine this was never mentioned by protagonists. In the U.S. the ever increasing production of new topologists in 1951–1975 was accompanied, in 1967–1974, by a funding cut of nearly 40% for research [Cohn 1986, 38].
6. One source for the emergence of ‘a new paradigm for making mathematics useful, mathematical modelling,’ has been examined in [Alberts 1994, 280]. For another viewpoint, see [Israel 1996].
7. For histories of catastrophe theory, see [Aubin forthcoming; Ekeland 1988; and Woodcock and Davis 1978].
8. Andronov's philosophical concerns leading to the concept of structural stability are found in the introduction to Andronov er al. [1966]. About Andronov, see [Diner 1992; and Dahan Dalmedico 1995].
9. [Thorn 1969], 333–334. For extended discussions of topological models in biology, see [Thorn 1975], ch. 9–11.
10. In modeling actual systems, many assumptions and idealizations always are involved. How one motivates them can vary. In some cases, philosophical arguments are used: e.g. nature selects the simplest equation consistent with hypotheses. Zeeman's gist was to justify with a theorem what hitherto had been merely postulated.
11. A deeper analysis of the reception, adaptation, and development of Smale's ideas in economics is called for, as it would provide fascinating insights into the processes by which topological practices entered the social sciences.
12. [Eckmann 1981], 643. Although this has not been attempted here, a linguistic analysis in terms of ‘pidgins’ and ‘Creoles’ might be enlightening for the study of the history of chaos [Galison 1997].
REFERENCES
Alberts, G. [1994] ‘On Connecting Socialism and Mathematics: Dirk Struik, Jan Burgers, and Jan Tinbergen’, Historia Mathematica 21, 280–305.
Andronov, A.A., Witt, A.A., and Khaikin, S.E., [1966] (1937) Theory of Oscillators, trans. F. Immirzi, Oxford, Pergamond; Reading: Addison-Wesley.
Atiyah, M., [1995] ‘Reflections on Geometry and Physics’, Surveys in Differential Geometry, 2, Proceedings of the Conference on Geometry and Topology Held at Harvard University, April 23–25, 1993, Sponsored by Lehigh University's Journal of Differential Topology, Boston, International Press, 1–6.
Aubin, D., [1997] The Withering Immortality of Nicolas Bourbaki: A Cultural Connector at the Confluence of Mathematics, Structuralism, and the Oulipo', Science in Context 10(2), 297–342. [1998a] A Cultural History of Catastrophes and Chaos: Around the ìnstitut des Hautes Etudes Scientifiques, France, Ph.D. dissertation, Princeton University, UMI 9817022.
[1998b] ‘Un pacte singulier entre mathématiques et Industrie. L'enfance chaotique de I'ïnstitut des Hautes Etudes Scientifique’, La Recherche, n° 313, 98–103.
'Forms of Explanations in the Catastrophe Theory of Rene Thorn: Topology, Morphogenesis, and Structuralism', in Wise, M.N., (ed.), Growing Explanations: Historical Perspecitive on the Sciences of Complexity, (to appear).
Bergé, P., Dubois, M., [1976] ‘Time Dependent Velocity in RayleighTîénard Convection: A Transition to Trubulence’, Optics Communications, 19, 129–33.
Bergé, P., Dubois M., Manneville, P., Pomeau, Y., [1980] ‘Intermittency in Rayleigh-Bénard Convection’, Journal de physique—Lettres, 41, 341—45.
Birkhoff, G.D., [1942] ‘Review of S. Lefschetz, Algebraic topology (Providence: AMS, 1942) and G.T. Whyburn, Analytic Topology (Providence: AMS, 1942)’, Science, 96, 581–584; (repr. Collected Papers, 3, 839–842).
[1943] ‘The Mathematical Nature of Physical Theories’, American Scientist, 31, 281–310; (repr. Papers, 2, 890–919).
Bott, R., [1890] ‘Marston Morse and his Mathematical Works’, Bulletin of the American Mathematical Society, 3, 907–50.
Browder, W., [1989] ‘Commentary on Topology’, A Century of Mathematics in America, Part II, ed. P. Duren, Providence, American Mathematical Society, 347–351.
Cohn, S.F., [1986] The Effects of Funding Changes upon the Rate of Knowledge Growth in Algebraic and Differential Topology, 1955–75', Social Studies of Sciences, 16, 23–56.
Collet, P., Eckmann, J.P., Koch, H., [1981] ‘Period Doubling Bifurcations for Families of Maps on Rn’, Journal of Statistical Physics, 25, 1–1.4.
Dahan Daimedico, A., [1995] ‘Le difficile heritage de Henri Poincaré en systèmes dynamiques’, Sonderdruck aus Henri Poincaré: Science et philosophic, Congrès international de Nice, 1994, Berlin, Akademie; Paris, Blanchard, 13–33.
[1996] ‘L'essor des mathématiques appliquées aux Etats-Unis: I'impact de la Seconde Guerre mondiale’, Revue d'histoire des mathématiques, 2, 149–213.
Debreu, G., [1959] Theory of Value: An Axiomatic Analysis of Economic Equilibrium, New Haven, Yale University Press.
Dieudonné, J., [1989] A History of Algebraic and Differential Topology, 1900–1960, Boston and Basel, Birkhäuser.
[1994] ‘Une brève histoire de la topologie', in Pier, J.P., (ed.), Development of Mathematics, 1900–1950, Boston and Basel, Birkhäuser, 35–155.
Diner, S-, [1992] ‘Les voies du chaos déterministe dans l'école russe', in Dahan Dalmedico, A., Chabert, J-L., Chemla, K., (eds.), Chaos et déterminisme, Paris, Seuil, 331–70.
Eckmann, J-P., [1981] ‘Roads to Turbulence in Dissipative Dynamical Systems’, Reviews of Modern Physics, 53, 643–654.
Ekeland, I., [1988] Calculus and the Unexpected, Chicago, University of Chicago Press.
Epple, M., [1998] Topology, Matter, and Space I: Topological Notions in 19th-century Natural Philosophy', Archives for History of Exact Sciences, 52, 297–392.
Feffer, L.B., [1997] ‘Mathematical Physics and the Planning of American Mathematics: Ideology and Institutions’, Historia Mathematica, 24, 66–85.
Froissart, M., [1966] ‘Applications of Algebraic Topology to Physics', in Goodman, R., Segal, I., (eds.), Mathematical Theory to Elementary Particles: Proceedings of the Conference Held at Dedham, Massachusetts, 1965, Cambridge, MIT Press., 19–28.
Galison, P., [1997] Image and Logic: A Material Culture of Microphysics, Chicago, University of Chicago Press. Henderson, J.C. de C, Maunders, E.A.W., [1969] ‘A Problem in Applied Topology: On the Selection of Cycles for the Flexibility Analysis of Skeletal Structures’, Journal of the Institute of Mathematics and Applications, 5, 254–269.
Hopf, E., [1942] ‘Abzweigung einer periodischen Lösung von eine stationaren Lösung eines Differentialsystems’, Berichten der Mathematisch-Physischen Klasse des Sachsischen Akademie der Wissenschaften zu Leipzig, 94, 1–22; Eng. Transl., in Marsden, J.E., McCracken, M., (eds.), The Hopf Bifurcation and Its Applications, New York, Springer, 163–93.
[1948] ‘A Mathematical Example Displaying Features of Turbulence’, Communications on Applied Mathematics 1, 303–322.
Hopf, H., [1960] ‘The work of R. Thom’, Proceedings of the International Congress of Mathematicians [Edinburgh, August 1958], Cambridge, Cambridge University Press, lx-lxiv.
Houzel, C, [1979] ‘Les mathématiciens retournent au concret’, La Recherche, n° 100, 508–509.
Israel, G., [1996] La Mathématisation du reel, Paris, Seuil.
Jaffe, A., Quinn, F., [1993–1994] ‘Theoretical Mathematics: Toward a Cultural Synthesis of Mathematics and Theoretical Physics’, Bulletin of the American Mathematical Society, 19 (1993), 1–13; and the various responses in ibid. 30 (1994), 178–207.
Landau, L., [1944] ‘On the Problem of Turbulence’, Doklady Akademi Nauk SSSR 44, 311–314.
Lefschetz, S., [1986] ‘A Page of Mathematical Autobiography', in Sundaraman, D., (ed.), The Lefschetz Centennial Conference: Proceedings of the Conference Held December 10–14, 1984, I, Providence, American Mathematical Society, 1–26.
Lichnérowicz, A., [1995] Rapport pour la creation d'une chaire d'Algèbre et Géométrie, Assemblée des professeurs (27 November). Archives du College de France, Paris. Document G-iv-m 20R,
Manneviile, P., Pomeau, Y., [1980] ‘Different Ways to Turbulence in Dissipative Dynamical Systems’, Physica ID, 219–226.
Peixoto, M., (ed.) [1973] Dynamical Systems: Proceedings of a Symposium Held at the University of Bahia. New York, Academic Press.
Pomeau Y., Manneviile, P., [1979] ‘Intermittency: A Generic Phenomenon at the Onset of Turbulence', in Laval, G., Grésillon, D., (eds.), Intrinsic Stochasticity in Plasmas, Orsay, Editions de physique Courtaboeuf, 330–340.
[1980] ‘Intermittent Transition to Turbulence in Dissipative Dynamical Systems’, Communications in Mathematical Physics, 74, 189–197.
Pont, J.C, [1974] La Topologie algébrique des origines à Poincaré, Paris, Presses Universitaires de France.
Ruelle, D., [1972] ‘Strange Attractors as a Mathematical Explanation of Turbulence’ in Rosenblatt, M., van Atta, C, (eds.), Statistical Models and Turbulence: Proceedings of the Symposium at La Jolla, 1971, Berlin, Springer, 292–299.
Ruelle, D., Takeπs, F., [1971] ‘On the Nature of Turbulence’, Communications in Mathematical Physics, 20, 167–192; 23, 343–344.
Smale, S., [1967] ‘Differentiabìe Dynamical Systems–. Bulletin of the American Mathematical Society, 73, 747–817. (repr. [Smale 1980], 1–82).
[1969/70] ‘Stability and Genericity in Dynamical Systems’, Séminaire Bourbaki, 22, (374), Berlin, Springer, Lecture Notes in Mathematics 180 (repr. [Smale 1980], 90–94).
[1972] ‘Personal Perspectives on Mathematics and Mechanics', in Rice, S.A., et al., (eds.), Statistical Mechanics: New Concepts, New Problems, New Applications, Chicago, Uinvetsity of Chicago Press, 3–12. (repr. [Smale 1980], 95–105).
[1973] ‘Global Analysis and Economics I: Pareto Optimum and a Generalization of Morse Theory', in Peixoto [1973], 531–44.
[1980] The Mathematics of Time: Essays on Dynamical Systems, Economic Processes, and Related Topics, New York, Springer.
[1990] ‘The Story of the Higher Dimensional Poincaré Conjecture (What Actually Happened on the Beaches of Rio)’, Mathematical Intelligencer, 12(2), 44–51, (repr. In Hirsch, M.W., et al., (eds.), From Topology to Computation: Proceedings of the Smalefest, New York, Springer, 1993, 27–40.
Thorn, R., [1969] ‘Topological Models in Biology’, Topology, 8, 313–35.
[1973] ‘Langage et catastrophes: elements pour une sémantique topologique', in Peixoto [1973],
619–654; and in Mathematical Models of Morphogenesis, transl. Brooks, W.M., Rand, D., Chichester, Ellis Horwood, 1983, 214–243.
[1975] (1972), Structural Stability and Morphogenesis: Outline of a General Theory of Models, trans. D.H. Fowler, Reading: Benjamin.
[1976] ‘The Two-Fold Way of Catastrophe Theory’ in Hilton, P., (ed.), Structural Stability, the Theory of Catastrophes, and Applications, Berlin, Springer, 235–252.
[1977a] ‘Rene Thorn répond à Lévy-Leblond sur la théorie des catastrophes’, Critique, 33, 675–681.
[1977b] ‘Structural Stability, Catastrophe Theory, and Applied Mathematics’, SÌAM Review, 19, 189–201.
[1983] Paraboles et catastrophes. Entretiens sur les mathématiques, la science et la philosophic realises par G. Giorello et S. Morini, Paris, Flammarion; (orig. Italian ed. 1980).
[1991] Prédire n'est pas explìquer, interview by Émile Noel, Paris, Eshel.
Velarde, M.G., [1981] ‘Steady States, Limit Cycles and the Onset of Turbulence: A Few Model Calculations and Exercises’ in Riste, T., (ed.), Nonlinear Phenomena at Phase Transitions and Instabilities, New York, Plenum, 205–247.
Warwick, A., [1992] ‘Cambridge Mathematics and Cavendish Physics: Cunningham, Campbell, and Einstein's Relativity 1905–1911', Studies in the History and Philosophy of Science, 23, 625–656; 24, 1–25.
Woodcock, A., Davis, M., [1978] Catastrophe Theory, New York, Dutton.
Zahler, R.S., Sussrnann, H.J., [1977] ‘Claims and Accomplishments of Applied Catastrophe Theory’, Nature, 269, 759–763.
Zeeman, E.C., [1964a] ‘Les mathématiques et la pensée ctéatrice’, Sciences et Venseignement des sciences, 5(34), 11–14.
[1964b] ‘Causality Implies the Lorentz Group’, Journal of Mathematics Physics, 5, 490—494.
[1965] ‘Topology of the Brain’, Conference on Mathematics and Computer Science in Biology and Medicine (MRC, Oxford, July 1964) , London, Her Majesty's Stationary Office, 277–311.
[1973] ‘Differential Equations for the Heartbeat and Nerve Impulse’ in Peixoto [1973], 683–741; and in Zeeman [1977], 81–140.
[1977] Catastrophe Theory: Selected Papers, 1972–1977, Reading: Addison-Wesley.
