© Marius Iulian Mihailescu and Stefania Loredana Nita 2021
M. I. Mihailescu, S. L. NitaCryptography and Cryptanalysis in MATLABhttps://doi.org/10.1007/978-1-4842-7334-0_6

6. Classic Cryptography

Marius Iulian Mihailescu1   and Stefania Loredana Nita1
(1)
Bucharest, Romania
 

This chapter provides an introduction to classic cryptography. It explains the symmetric class of ciphers, whereby the encryption key is the same for both operations—encryption and decryption. Such ciphers are Caesar, Vigenère, Hill, and others. The main goals of this chapter are to give you a clear understanding of the main symmetric cryptographic mechanisms and to provide you with proper implementations in MATALB. These ciphers are not secure and so are not used anymore, but they are good for understanding the main concepts involved in cryptography.

Symmetric Cryptography

Generally speaking, classic cryptography ciphers/algorithms are known as symmetric systems. This is because both participants involved in the communication process use the same cryptographic key. Another important aspect, which is vital for the communication (see Figure 6-1), is based on the fact that once you find the encryption key (Enck), the decryption key (Deck) can be found/computed very quickly by computing the inverse function; see [1] and [2].

Symmetric encryption ciphers can be divided in two main categories: permutation ciphers and substitution ciphers . A partial list includes the following symmetric algorithms, in ascending order of complexity: the Atbash Cipher, ROT13, the Caesar Cipher, the Affine Cipher, the Polybius Cipher, the Vigenère Cipher, the Hill Cipher, and Playfair. Of course, this list can be improved by adding other classical ciphers and some particular cases of the main ones. A comprehensive list can be seen at [12] and [13]. For more details about symmetric cryptography and algorithms, the following resources should be consulted in parallel: [2], [5], and [6].
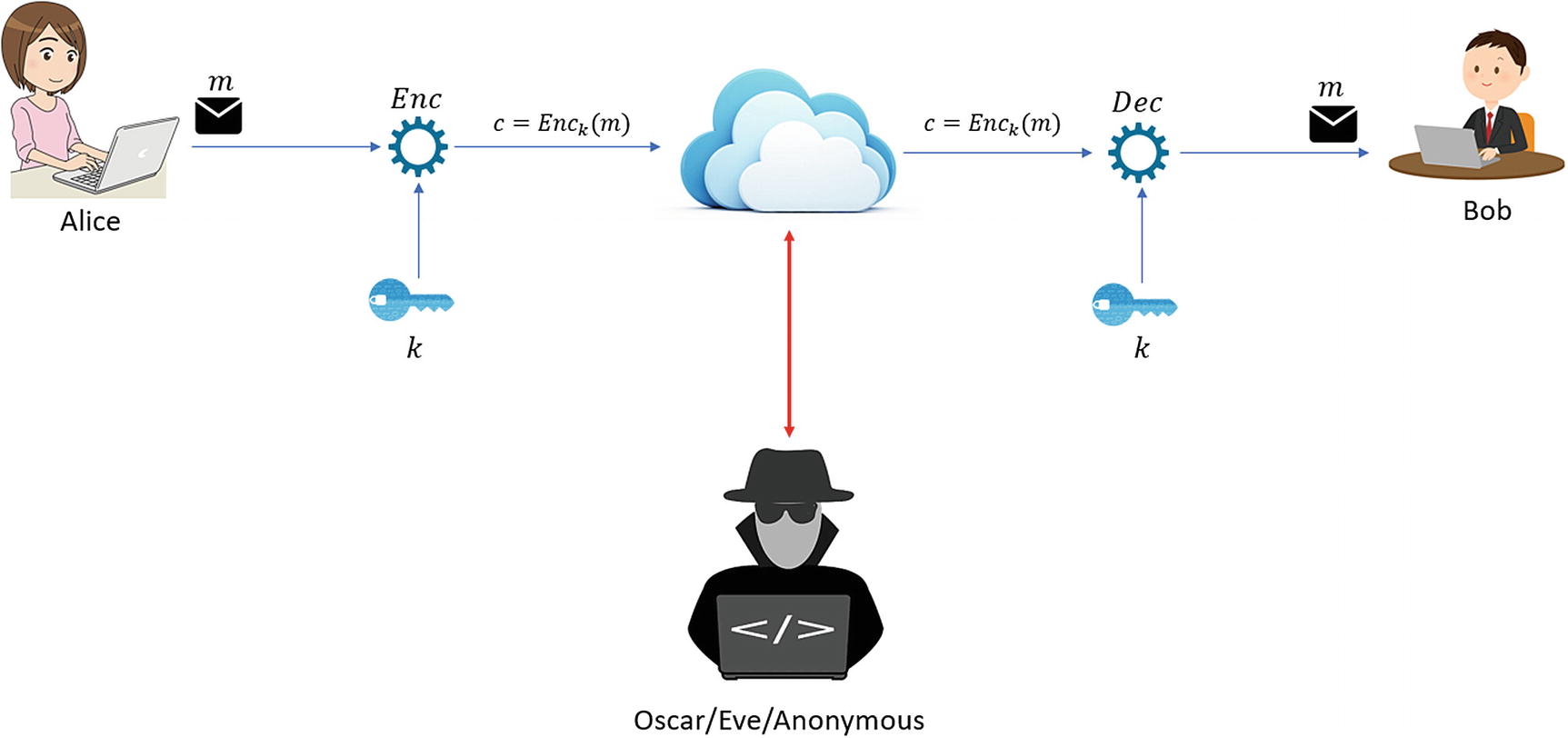
../images/500692_1_En_6_Chapter/500692_1_En_6_Fig1_HTML.jpg
Figure 6-1

Overview of a practical scenario for symmetric encryption1

Figure 6-1 shows a general scenario that illustrates the communication process in classic cryptography (if it is used in a real communication process). The same key is used by Alice and Bob to encrypt and decrypt the message. If a malicious user gains access to the key, the entire communication process can easily be corrupted.

Classic Ciphers

This section covers the basic implementations in MATLAB of the Caesar, Vigenère, and Hill classic cryptography ciphers.

These implementations are straightforward yet provide the necessary elements for future implementations.

The goal of this section is to provide you with some basic concepts in implementing cryptography algorithms/ciphers, especially using MATLAB. This section can serve as a quick review of the main concepts. As mentioned, these kinds of algorithms/ciphers are not used anymore in real environments, but studying them can help improve your programming skills, in this case, specifically for MATLAB.

The Caesar Cipher

The Caesar Cipher represents one of the simplest and best-known ciphers. It’s a substitution cipher, whereby each letter from the plaintext is shifted a certain number of positions (characters) in the alphabet. As an example, if we shift the alphabet two spaces, the letter “A” is replaced with “C,” the letter “B” is replaced with “D,” and so on. As you will see, the Caesar Cipher is used by other classical ciphers, such as the Vigenère Cipher. The main steps of the Caesar Cipher are included as a step in the Vigenère Cipher. Another cipher that uses the Caesar encryption process is known as ROT13, which uses 13 as the offset.

Example

When we want to send a message from a person to another, the same cryptographic key is used by both partners engaged in this communication process. In the Caesar Cipher, the key is the number of characters used to shift the alphabet.

Example 6-1 represents the encryption and decryption phases involved in the Caesar Cipher. For this, we have chosen a cryptographic key (k) of 3. The text that is encrypted is welcome to professional cryptography with matlab.
plaintext:   welcome to professional cryptography with matlab
ciphertext:  zhofrph wr surihvvlrqdo fubswrjudskb zlwk pdwode
Example 6-1

Caesar Encryption Procedure

As you can see in Example 6-1, the encryption process is very simple, as each plaintext character is shifted in the alphabet by three letters.

The decryption operation is very easy as well, simply using an offset of -3 (see Example 6-2).
   alphabet (plain):   ABCDEFGHIJKLMNOPQRSTUVWXYZ
   cipher:             DEFGHIJKLMNOPQRSTUVWXYZABC
Example 6-2

Encryption/Decryption Operations

If a different key is used (except k = 3), the decryption will be totally different.

Mathematical Background

The first step translates the characters to numbers (e.g., a = 0, b = 1, c = 2, d = 3, e = 4, …, z = 25). At this point, we can represent the encryption function for each of the characters from the plaintext as e(ci), where ci represents the character we are encrypting. The mathematical function can be represented as follows:
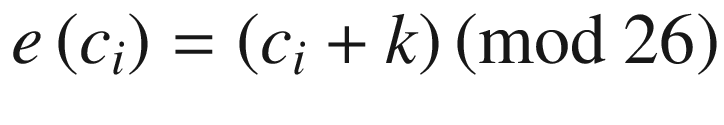
$$ eleft({c}_i ight)=left({c}_i+k ight)left(mathit{operatorname{mod}} 26 ight) $$
The result of the encryption function is represented by a number that’s translated back to a letter. The decryption function is as follows:
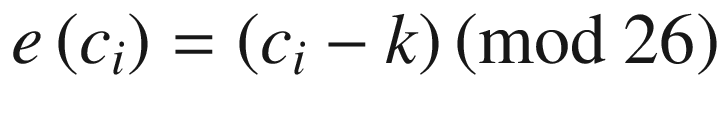
$$ eleft({c}_i ight)=left({c}_i-k ight)left(mathit{operatorname{mod}} 26 ight) $$

Cryptanalysis

It is very easy to crack the Caesar Cipher with the help of automated tools [10]. There are only 25 possible keys representing the alphabet (0-25). Brute-force decryption methods can crack these types of encrypted messages in milliseconds.

A brute-force method determines the fitness value of a chunk of the decrypted text. The process determines if a chunk of encrypted text fits the unencrypted text. It computes the statistics based on the decrypted text and compares those statistics to the ones computed from the standard English text. The fitness function gives us a numeric value, and the higher the value is, the greater probably a particular key is the right one. If you’re using this technique, it’s best to use quadgram statistics as a fitness measure [9]. The steps are as follows:

  • Determine the statistics in the unencrypted text.

  • Compute the probability that the ciphertext is the same, using the distribution.

Implementing the Caesar Cipher

Listing 6-1 shows an implementation of the Caesar Cipher. A similar implementation can be found in [7] by Professor Alexander Stanoyevitch. Because the steps of the encryption are quite straightforward and standard, the only different or extra steps that can be added are represented by validating the inputs.

Let’s quickly review the implementation of the Caesar Cipher in Listing 6-1. As you can see, the main elements provided by the user are represented by the plaintext that we want to encrypt (the clear_text variable in Line 5) and the cryptographic key (the key in Line 8). It is very important to determine the alphabet structure (see Line 2, the alphabet variable) before proceeding with the encoding (encryption) phase.

As you can see in Line 10, we are testing if the key is situated between 0 and 26 and in Line 11 there is a modulo computation in Z26.

Line 14 contains a Boolean variable, breaking_loop, which is initialized with 0. As the name suggests, the variable is used to exit a loop when criteria is found, after which its value changes to 1 (see Line 20). Another Boolean variable is iteration_flag, which is initialized with 1 and declared in Line 16. It’s used in a while loop (Line 18) to determine if the length of the plaintext entered by the user is less than or equal to 1. Between Lines 23 and 40, the encoding (encryption) process is taking place. As an example, we chose the plaintext welcometocryptography and initialized the key with 3. The output is shown in Figure 6-2.
 1   function console_output = caesarcipher()
 2
 3       alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i',
 4    'j', 'k', 'l', 'm', 'n', 'o','p', 'q', 'r', 's', 't', 'u',
 5    'v', 'w', 'x', 'y', 'z'];
 6       clear_text = input('Enter a text (plaintext) that you
 7   wish to encrypt it (eliminate the spaces): ','s');
 8
 9       key = input('Enter the key: ');
10
11       if key > 26 || key < 0
12           key = mod(key,26);
13       end
14
15       breaking_loop = 0;
16       iteration_flag = 1;
17
18       while iteration_flag <= length(clear_text)
19          if ismember(clear_text(iteration_flag),'A':'Z') == 1
20               breaking_loop = 1;
21               console_output = exception_message;
22
23           elseif isletter(clear_text(iteration_flag)) == 1
24               y =
25   strfind(alphabet,clear_text(iteration_flag));
26               z = y+key;
27                   if z > 26
28                       z = z - 26;
29                   end
30               console_output(iteration_flag) = alphabet(z);
31
32           elseif isletter(clear_text(iteration_flag)) == 0
33               if plain(iteration_flag) == ' '
34                   console_output(iteration_flag) =
35    clear_text(iteration_flag);
36               else
37                   breaking_loop = 1;
38                   console_output = exception_message;
39               end
40           end
41
42           iteration_flag = iteration_flag+1;
43           if breaking_loop == 1
44               break
45           end
46       end
47   end
Listing 6-1

Implementation of the Caesar Cipher

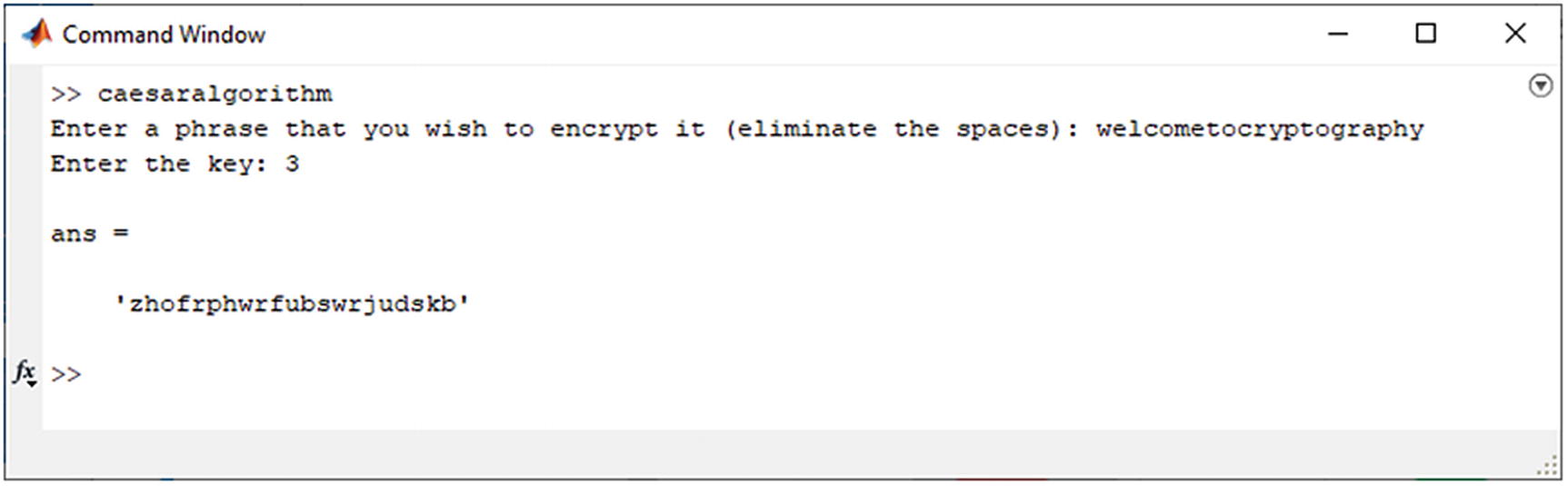
../images/500692_1_En_6_Chapter/500692_1_En_6_Fig2_HTML.jpg
Figure 6-2

Encryption output of the Caesar Cipher

The Vigenère Cipher

The Vigenère Cipher is a polyalphabetic substitution cipher. The cipher was considered unbreakable for 300 years, and studies of it are still being published in different journals and conference proceedings.

The first successful attack on the Vigenère Cipher was published in 1863 by Friedrich Kasiski, even though Charles Babbage had designed a successful attack some years before. Another important aspect that is worth mentioning is the fact that Gilbert Vernam worked on the cipher in the early 1900s, proposing and designing what we know now as OTP (One Time Pad). His work had a great impact on current authentication systems.

Example

As an example, we use WELCOME TO THE WORLD OF CRYPTOGRAPHY as the text that we want to encrypt. The cryptographic key is APRESS.

The Vigenère Cipher uses the block in Table 6-1 to encode the plaintext. This table is known as tabula recta.
Table 6-1

Tabula Recta

../images/500692_1_En_6_Chapter/500692_1_En_6_Figa_HTML.jpg

The first step is to repeat the keyword above the plaintext (for this demonstration will skip the blank spaces) until it has the same length. It should look like this:
Key:           APRESSAPRESSAPRESSAPRESSAPRESSA
Plaintext:     WELCOMETOTHEWORLDOFCRYPTOGRAPHY
The procedure to encode the message is based on a simple substitution. It takes each character from the plaintext and locates it on the first column from the table in Figure 6-3, then continues with the first letter from the key and locates it on the first row. Once it identifies the letter from the plaintext on the column and the key on the row, it continues to where they intersect and finds the corresponding letter, as shown in Figure 6-3.
../images/500692_1_En_6_Chapter/500692_1_En_6_Fig3_HTML.jpg
Figure 6-3

The encryption process

As an example, we took the first word of the plaintext (WELCOME) and encrypted it using the method described. For the rest of the plaintext, the procedure is the same. The result of the encryption operation is WTCGGEE, as you can see in Figure 6-3.

The encryption of the plaintext is as follows:
Key:           APRESSAPRESSAPRESSAPRESSAPRESSA
Plaintext:     WELCOMETOTHEWORLDOFCRYPTOGRAPHY
----------------------------------------------
Encryption:    WTCGGEEIFXZWWDIPVGFRICHLOVIEHZY

Mathematical Background

Some important mathematical aspects that are necessary for practical implementations are worth mentioning here; see Table 6-2.
Table 6-2

Notations

Notation

Definition

P

The space in the plaintext

C

The space in the ciphertext

K

The space in the keys

c1, c2, …, cm

The characters that will be encrypted from the plaintext

h1, h2, …, hm

The encrypted values of the characters

k

The cryptographic key

enck

The encryption function

deck

The decryption function

As a first step, we need to define m as a fixed positive integer. The next step is to define P = C = K = (Z26)m. For a specific key, K = (key1, key2, …, keym), let’s define the following:
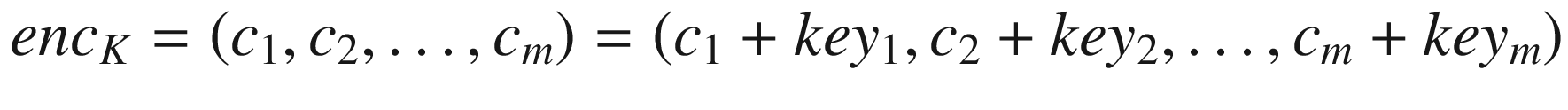
$$ en{c}_K=left({c}_1,{c}_2,dots, {c}_m ight)=left({c}_1+ ke{y}_1,{c}_2+ ke{y}_2,dots, {c}_m+ ke{y}_m ight) $$
and
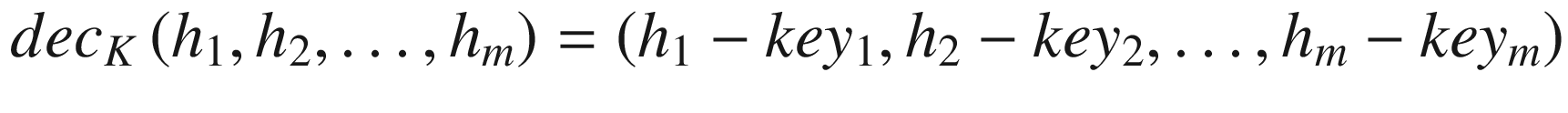
$$ de{c}_Kleft({h}_1,{h}_2,dots, {h}_m ight)=left({h}_1- ke{y}_1,{h}_2- ke{y}_2,dots, {h}_m- ke{y}_m ight) $$

where the entire set of operations is computed in Z26.

Suppose in the following example, K = (7, 3). Let’s compute 7−1 mod 26 = 15. The encryption function is enck(c) = 7x + 3, and the decryption function is deck(h) = 15(h − 3) = 15h − 19.

An important step is to verify if deck(enck(c)) = x, ∀c ∈ Z26. By performing computations in Z26, we get the following:
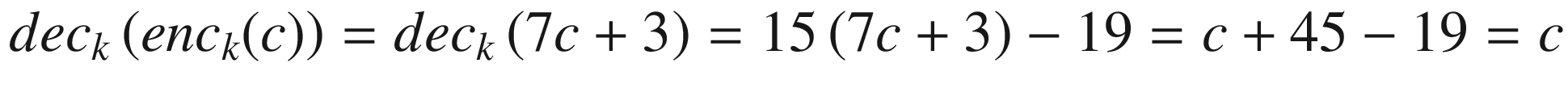
$$ de{c}_kleft( en{c}_k(c) ight)= de{c}_kleft(7c+3 ight)=15left(7c+3 ight)-19=c+45-19=c $$

Implementing the Vigenère Cipher

Providing an implementation of the Vigenère Cipher is easier than for the Caesar Cipher. Another implementation provided by Professor Alexander Stanoyevitch is shown in [7]. Comparing it with the version provided in Listing 6-2, there are a couple of similarities at first sight. This is due to the main steps of the cipher and the unique way of implementing them, not only in MATLAB but also in other programming languages; see [3], [4], and [6].

The code is self-explanatory. To invoke the encryption function, the user must provide the following call in the Command Prompt (see Figure 6-4):
   Vigenere_Encryption('welcometocryptography', 'apress')
The code from Listing 6-2 has a couple of easy steps; one of the main steps is to convert the encryption key to lowercase letters (see Line 3) and represent them as an array. The next step computes the length of the encryption key (see Line 4). Further, the procedure for encryption is based on computing the modulo operation between the index of each character from the plaintext and the length of the encryption key (see Lines 5 and 6).
 1   function output_string =
 2   Vigenere_Encryption(plaintext,encryption_key)
 3   Array = encryption_key - 'a';
 4   keylength = length(encryption_key);
 5   for i=1:length(plaintext)
 6      ishift = mod(i,keylength);
 7      if ishift == 0, ishift = keylength; end
 8      output_string(i) =
 9   Shift_Encryption(plaintext(i),Array(ishift));
10   end
Listing 6-2

Implementation of the Vigenère Cipher – Encryption Function

The Shift Encryption function, which is an important function that we kept from [7], is shown in Listing 6-4; its main purpose is to perform the shifting operation, as described in the theoretical background.
1   function OutputString =
2   Shift_Encryption(plaintext,moduloInteger)
3   Array = plaintext - 'a';
4   OutputArray = mod( Array + moduloInteger, 26);
5   OutputString = char(OutputArray + 'A');
Listing 6-3

Shift Encryption Function

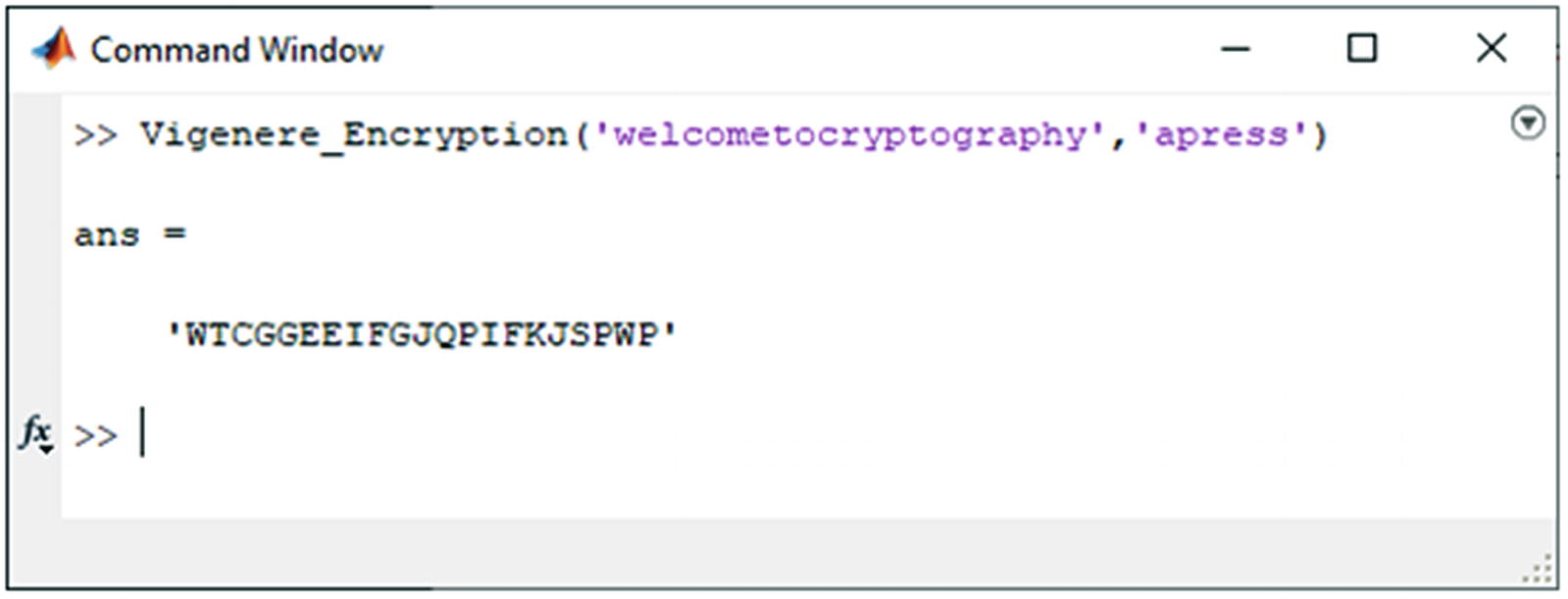
../images/500692_1_En_6_Chapter/500692_1_En_6_Fig4_HTML.jpg
Figure 6-4

Encryption result of the Vigenère Cipher

In Listing 6-4, we provide an implementation of the decryption process as being the reverse procedure of encryption. Figure 6-5 shows the output of the decryption function; it is a very good way to check that the encryption function worked as expected.
 1   function output_vigenere_decryption =
 2   Vigenere_Decryption(plaintext,decryptionKey)
 3
 4   Array = decryptionKey - 'a';
 5   decryption_key = length(decryptionKey);
 6   lowercase_string = char((plaintext - 'A') + 'a');
 7   for i=1:length(plaintext)
 8      ishift = mod(i,decryption_key);
 9      if ishift == 0, ishift = decryption_key; end
10      output_vigenere_decryption(i) =
11           Shift_Encryption(lowercase_string(i),-
12   Array(ishift));
13   end
14   output_vigenere_decryption =
15   char((output_vigenere_decryption - 'A') + 'a');
Listing 6-4

Implementation of the Vigenère Cipher – Decryption Function

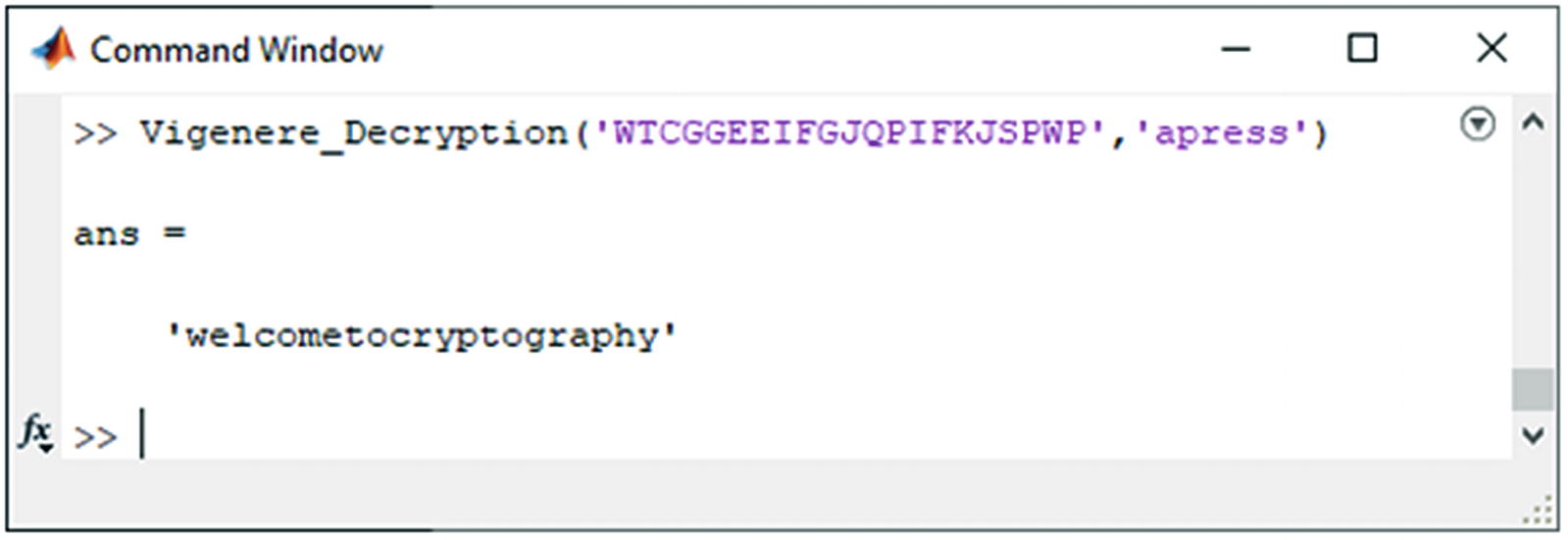
../images/500692_1_En_6_Chapter/500692_1_En_6_Fig5_HTML.jpg
Figure 6-5

Vigenère Cipher decryption result

The Hill Cipher

The Hill Cipher was designed in 1929 by Lester S. Hill as a polygraphic substitution cipher based on linear algebra. The main essence of the Hill Cipher is that it uses matrices and matrix multiplication to mix up the plaintext.

The system proposed by Hill was designed to use a series of gear wheels and chains. Unfortunately, the proposed device was never sold.

Example

Most of the Hill Cipher examples use linear algebra and number theory. The key in this encryption process has a matrix structure, as follows:
$$ left[2 6 8 12 14 1 3 19 9 ight] $$

This example has a size of 3 × 3. It can be any size, as long as the matrix is a square. As an example, let’s suppose that you want to encode the message WELCOME TO CRYPTOGRAPHY. To encrypt the message, you need to divide the plaintext into pieces that are three characters/letters long. Let’s consider the first three characters/letters from the message (plaintext), WEL, and write them as an array with numeric values that correspond to the letters: W = 22, E = 4, and L = 11.

Once we encode the letters into numbers, we need to do the matrix multiplication as follows:
$$ left[2 6 8 12 14 1 3 19 9 ight]left[22 4 11 ight]=left[156 331 241 ight]left(mathit{operatorname{mod}} 26 ight)=left[0 19 7 ight]= ATH $$

So, the encoding of WEL is ATH. This process is done for all blocks of letters from the plaintext. In some documentation, the plaintext is padded with extra letters to make it a whole number of blocks.

The interesting part is in the decryption. The main task is represented to find the inverse matrix modulo 26 as the decryption key. We want to convert ATH back to WEL. If the key that we used is a 3 × 3 matrix called K, the decryption key will use a 3 × 3 matrix K−1, which represents the inverse of K. The result will be as follows:
$$ {K}^{-1}=left[0 19 7 ight]left(mathit{operatorname{mod}} 26 ight)=left[22 4 11 ight]= WEL $$

Cryptanalysis

The Hill Cipher is very vulnerable to a known plaintext attack. Once you know the plaintext and the encrypted version of it, the key can be easily recovered. This is possible because everything is linear.

If you are dealing with a 2 × 2 case of the Hill Cipher, you can launch the attack by computing the frequencies of all the digraphs occurring within the encrypted version of the plaintext. It is very important to understand and to have some familiar knowledge of standard English digraphs, such as “th” and “he”. For more information about the cryptanalysis process, resource [8] is recommended, especially for professionals working with old manuscripts, documents, letters, etc.

Implementing the Hill Cipher

Implementing the Hill Cipher in different programming languages (e.g., C#, Java, or C++), as shown in [3] and [4], can be a real adventure due to the multiple steps that need to be achieved. When we are doing the implementation in MATLAB, things are straightforward, as shown in Listing 6-5. A similar version is provided by Professor Alexander Stanoyevitch in [7].

Listing 6-5 shows an example of an encryption function using the Hill Cipher. It is quite similar to [7], because the steps are standard, and the functions can be represented in a unique way. The user invokes the cipher with the following call as input from the Command Prompt:
            Hill_Encryption('welcome to apress',
                          '23 19 12; 0 11 1; 10 18 17')

Remember that the matrix given as the second parameter in the call must be inverse modulo Z26.

Let’s continue with a quick overview of the source code provided in Listing 6-5. We will start the analysis with Line 2, in which we compute the size of the matrix provided by the user as input (see Figure 6-6). In Line 3, we make sure that all the characters from the plaintext are lowercase letters. Once we have the entire array of characters, in Line 4 we compute the length. In Line 5, we compute a padded value (append_array_length) based on the modulo operation between the length of the array (plaintext) and the size of the square matrix (n).

Further, we compute the added length in Line 7 by subtracting the padded value from n. This operation is executed as long as the padded value (append_array_length) is greater than 0. In Line 8, we form the new array (plaintext). In Line 11, we compute the number of columns. In Line 12, we compute the reshaped array with the new structure, including the padded value, and in Lines 14 and 15, we output the result of the encryption.
1   function console_output = Hill_Encryption(plaintext,matrix)
2   [n n] = size(matrix);
3   Array = plaintext - 'a';
4   array_length = length(Array);
5   append_array_length = mod(array_length,n);
6   if append_array_length > 0
7       add_length = n - append_array_length;
8      Array(array_length + 1: array_length + add_length) = 13;
9   end
10
11   columns_number = length(Array)/n;
12   reshaped_array = reshape(Array, [n columns_number]);
13   ciphertext = mod(matrix*reshaped_array,26);
14   array_output = ciphertext(:)';
15   console_output = char(array_output + 'A');
Listing 6-5

The Hill Cipher Encryption Function

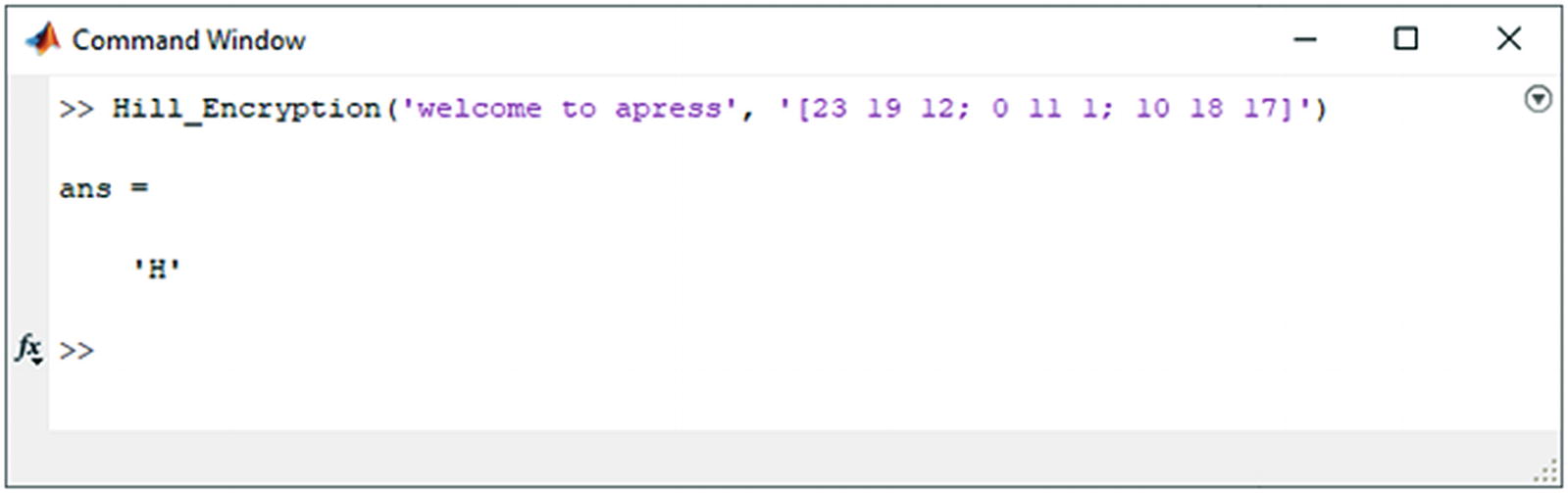
../images/500692_1_En_6_Chapter/500692_1_En_6_Fig6_HTML.jpg
Figure 6-6

Encryption output of the Hill Cipher

Conclusion

This chapter discussed symmetric cryptography as a main entry point into practical cryptography, providing basic information so you can acquire the basic programming skills you need in MATLAB.

For this purpose, we focused on the Caesar, Vigenère, and Hill Ciphers, as they are well-known ciphers in classic cryptography and are used often during the learning process.

References

  1. [1]

    Atanasiu, Adrian. Securitatea Informației – Volumul 1: Criptografie. InfoData, 2007. ISBN: 978-973-1803-16-6.

     
  2. [2]

    Menezes, A. J., et al. Handbook of Applied Cryptography. CRC Press, 1997.

     
  3. [3]

    Mihailescu, Marius Iulian, and Stefania Loredana Nita. Pro Cryptography and Cryptanalysis: Creating Advanced Ciphers with C# and .NET. Apress, 2021. DOI.org (Crossref), doi:10.1007/978-1-4842-6367-9.

     
  4. [4]

    Mihailescu, Marius Iulian, and Stefania Loredana Nita. Pro Cryptography and Cryptanalysis with C++20: Creating and Programming Advanced Ciphers. Apress, 2021. DOI.org (Crossref), doi:10.1007/978-1-4842-6586-4.

     
  5. [5]

    Paar, Christof, and Jan Pelzl. Understanding Cryptography: A Textbook for Students and Practitioners. Springer Berlin Heidelberg, 2010. DOI.org (Crossref), doi:10.1007/978-3-642-04101-3.

     
  6. [6]

    Schneier, Bruce. Applied Cryptography: Protocols, Ciphers, and Source Code in C. 20th anniversary edition, Wiley, 2015.

     
  7. [7]

    Stanoyevitch, Alexander. Introduction to Cryptography with Mathematical Foundations and Computer Implementations. CRC Press, 2011. ISBN: 979-8651423514.

     
  8. [8]

    Practical Cryptography (website). Hill Cipher - http://practicalcryptography.com/ciphers/classical-era/hill/.

     
  9. [9]

    Practical Cryptography (website). Quadgram Statistics as a Fitness Measure - http://practicalcryptography.com/cryptanalysis/text-characterisation/quadgrams/.

     
  10. [10]

    Practical Cryptography (website). Cryptanalysis of Caesar Cipher - http://practicalcryptography.com/cryptanalysis/stochastic-searching/cryptanalysis-caesar-cipher/.

     
  11. [11]

    Practical Cryptograhy (website). Caesar Cipher - http://practicalcryptography.com/ciphers/caesar-cipher/.

     
  12. [12]

    Practical Cryptography (website). Ciphers - http://practicalcryptography.com/ciphers/.

     
  13. [13]

    Cipher Types (website). https://www.cryptogram.org/resource-area/cipher-types/.

     
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.16.66.156