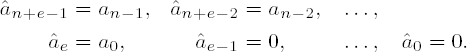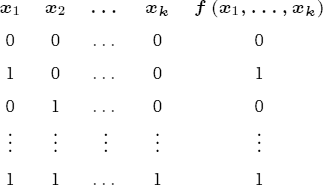The simplest way to multiply a number a with the representation a = (a_n−1a_n−2 . . . a₀)_B to the base B by a power B^e is to "shift a to the left by e digits." This works with the binary representation exactly as it does in our familiar decimal system:

Equation 7.1. 

where

Equation 7.2. 

For B = 2 this corresponds to multiplication of a number in binary representation by 2^e, while for B = 10 it corresponds to multiplication by a power of ten in the decimal system.

In the analogous procedure for whole-number division by powers of B the digits of a number are "shifted to the right":

Equation 7.3. 

where

Equation 7.4. 

For B = 2 this corresponds to integer division of a number in binary representation by 2^e, and the analogous result holds for other bases.

Since the digits of CLINT objects are represented in memory in binary form, CLINT objects can easily be multiplied by powers of two by shifting left, where the next digit to the right is shifted into each place where a digit has been shifted left, and the binary digits left over on the right are filled with zeros.

In an analogous way CLINT objects can be divided by powers of two by shifting each binary digit to the right into the next lower-valued digit. Digits left free at the end are either filled with zeros or ignored as leading zeros, and at each stage in the process (shifting by one digit) the lowest-valued digit is lost.

The advantage of this process is clear: Multiplication and division of a CLINT object a by a power of two 2^e are simple, and they require at most e [log_B a] shift operations to shift each USHORT value by one binary digit. Multiplication and division of a by a power B^e uses only [log_B a] operations for storing USHORT values.

In the following we shall present three functions. The function shl_l() executes a rapid multiplication of a CLINT number by 2, while the function shr_l() divides a CLINT number by 2 and returns the integer quotient.

Lastly, the function shift_l() multiplies or divides a CLINT type a by a power of two 2^e. Which operation is executed is determined by the sign of the exponent e of the power of two that is passed as argument. If the exponent is positive, then the operation is multiplication, while if it negative, then division is carried out. If e has the representation e = Bk + l, l < B, then shift_l() carries out the multiplication or division in (l + 1) [log_B a] operations on USHORT values.

All three functions operate modulo (N_max + 1) on objects of CLINT type. They are implemented as accumulator functions, and thus they change their CLINT operands in that they overwrite the operand with the result of the operation. The functions test for overflow, respectively underflow. However, in shifting, underflow cannot really arise, since in those cases where more positions are to be shifted than there are digits the result is simply zero, almost as it is in real life. The status value E_CLINT_UFL for underflow then merely indicates that there was less to shift than was required, or, in other words, that the power of two by which division was to be carried out was larger than the dividend, and so the quotient is zero. The three functions are implemented in the following manner.

int
shl_l (CLINT a_l)
{
 clint *ap_l, *msdptra_l;
 ULONG carry = 0L;
 int error = E_CLINT_OK;

 RMLDZRS_L (a_l);
 if (ld_l (a_l) >= (USHORT)CLINTMAXBIT)
  {
   SETDIGITS_L (a_l, CLINTMAXDIGIT);
   error = E_CLINT_OFL;
  }
 msdptra_l = MSDPTR_L (a_l);
 for (ap_l = LSDPTR_L (a_l); ap_l <= msdptra_l; ap_l++)
  {
   *ap_l = (USHORT)(carry = ((ULONG)*ap_l << 1) | (carry >> BITPERDGT));
  }
 if (carry >> BITPERDGT)
  {
   if (DIGITS_L (a_l) < CLINTMAXDIGIT)
    {
     *ap_l = 1;
     SETDIGITS_L (a_l, DIGITS_L (a_l) + 1);
     error = E_CLINT_OK;
    }

else
      {
       error = E_CLINT_OFL;
      }
   }
  RMLDZRS_L (a_l);
  return error;
}

int
shr_l (CLINT a_l)
{
 clint *ap_l;
 USHORT help, carry = 0;

 if (EQZ_L (a_l))
  return E_CLINT_UFL;

 for (ap_l = MSDPTR_L (a_l); ap_l > a_l; ap_l--)
  {
   help = (USHORT)((USHORT)(*ap_l >> 1) | (USHORT)(carry <<
                                          (BITPERDGT - 1)));
   carry = (USHORT)(*ap_l & 1U);
   *ap_l = help;
  }
 RMLDZRS_L (a_l);
 return E_CLINT_OK;
}

int
shift_l (CLINT n_l, long int noofbits)
{
 USHORT shorts = (USHORT)((ULONG)(noofbits < 0 ? -noofbits : noofbits) / BITPERDGT);
 USHORT bits = (USHORT)((ULONG)(noofbits < 0 ? -noofbits : noofbits) % BITPERDGT);
 long int resl;
 USHORT i;
 int error = E_CLINT_OK;

 clint *nptr_l;
 clint *msdptrn_l;

 RMLDZRS_L (n_l);
 resl = (int) ld_l (n_l) + noofbits;

if (*n_l == 0)
 {
  return ((resl < 0) ? E_CLINT_UFL : E_CLINT_OK);
 }
if (noofbits == 0)
 {
  return E_CLINT_OK;
 }

if ((resl < 0) || (resl > (long) CLINTMAXBIT))
  {
   error = ((resl < 0) ? E_CLINT_UFL : E_CLINT_OFL); /*underflow or overflow*/
  }

 msdptrn_l = MSDPTR_L (n_l);

 if (noofbits < 0)
  {

shorts = MIN (DIGITS_L (n_l), shorts);
  msdptrn_l = MSDPTR_L (n_l) - shorts;
  for (nptr_l = LSDPTR_L (n_l); nptr_l <= msdptrn_l; nptr_l++)
   {
    *nptr_l = *(nptr_l + shorts);
   }
  SETDIGITS_L (n_l, DIGITS_L (n_l) - (USHORT)shorts);
  for (i = 0; i < bits; i++)
   {
    shr_l (n_l);
   }
 }
else
 {

if (shorts < CLINTMAXDIGIT)
   {
    SETDIGITS_L (n_l, MIN (DIGITS_L (n_l) + shorts, CLINTMAXDIGIT));
    nptr_l = n_l + DIGITS_L (n_l);
    msdptrn_l = n_l + shorts;

    while (nptr_l > msdptrn_l)
     {
      *nptr_l = *(nptr_l - shorts);
      --nptr_l;
     }

    while (nptr_l > n_l)
     {
      *nptr_l-- = 0;
     }

    RMLDZRS_L (n_l);

    for (i = 0; i < bits; i++)
     {
       shl_l (n_l);
      }
    }
   else
    {
     SETZERO_L (n_l);
    }
  }
 return error;
}

The FLINT/C package contains functions that allow the built-in bitwise C operators &, |, and ˆ to be used for the type CLINT as well. However, before we program these functions we would like to understand what their implementation will net us.

From a mathematical viewpoint we are looking at relations of the generalized Boolean functions f : { 0, 1 }^k → { 0, 1 } that map a k-tuple (x₁, . . . , x_k) € { 0, 1 }^k to the value 0 or 1. The effect of a Boolean function is usually presented in the form of a table of values such as that shown in Table 7-1.

Table 7-1. Values of a Boolean function

For the bitwise relations between CLINT types we first regard the variables as bit vectors (x₁, . . . , x_n), and furthermore, the function values of the Boolean functions will be formed into a sequence. Thus we have functions

Equation 7.5. 

that map n-bit variables

Equation 7.6. 

with

Decisive for the operation of the function fmacr is the definition of the partial functions f_i, each of which is defined in terms of a Boolean function f. For the CLINT functions and_l(), or_l(), and xor_l() the Boolean functions that are implemented are defined as in Tables 7-2 through 7-4.

The implementations of these Boolean functions in the three C functions and_l(), or_l(), and xor_l() do not actually proceed bitwise, but process the digits of CLINT variables by means of the standard C operators &, |, and ˆ. Each of these functions accepts three arguments of CLINT type, where the first two are the operands and the last the result variable.

void
and_l (CLINT a_l, CLINT b_l, CLINT c_l)
{
 CLINT d_l;
 clint *r_l, *s_l, *t_l;
 clint *lastptr_l;

if (DIGITS_L (a_l) < DIGITS_L (b_l))
 {
  r_l = LSDPTR_L (b_l);
  s_l = LSDPTR_L (a_l);
  lastptr_l = MSDPTR_L (a_l);
 }
else
 {
  r_l = LSDPTR_L (a_l);
  s_l = LSDPTR_L (b_l);
  lastptr_l = MSDPTR_L (b_l);
 }

t_l = LSDPTR_L (d_l);
SETDIGITS_L (d_l, DIGITS_L (s_l - 1));

while (s_l <= lastptr_l)
 {
  *t_l++ = *r_l++ & *s_l++;
 }

cpy_l (c_l, d_l);
}

void
or_l (CLINT a_l, CLINT b_l, CLINT c_l)
{
 CLINT d_l;
 clint *r_l, *s_l, *t_l;
 clint *msdptrr_l;
 clint *msdptrs_l;

if (DIGITS_L (a_l) < DIGITS_L (b_l))
 {
  r_l = LSDPTR_L (b_l);
  s_l = LSDPTR_L (a_l);
  msdptrr_l = MSDPTR_L (b_l);
  msdptrs_l = MSDPTR_L (a_l);
 }
else
 {
  r_l = LSDPTR_L (a_l);
  s_l = LSDPTR_L (b_l);
  msdptrr_l = MSDPTR_L (a_l);
  msdptrs_l = MSDPTR_L (b_l);
 }
t_l = LSDPTR_L (d_l);
SETDIGITS_L (d_l, DIGITS_L (r_l - 1));

while (s_l <= msdptrs_l)
 {
  *t_l++ = *r_l++ | *s_l++;
 }

while (r_l <= msdptrr_l)
 {
  *t_l++ = *r_l++;
 }
cpy_l (c_l, d_l);
}

void
xor_l (CLINT a_l, CLINT b_l, CLINT c_l)
{
 CLINT d_l;
 clint *r_l, *s_l, *t_l;
 clint *msdptrr_l;
 clint *msdptrs_l;

 if (DIGITS_L (a_l) < DIGITS_L (b_l))
  {
   r_l = LSDPTR_L (b_l);
   s_l = LSDPTR_L (a_l);
   msdptrr_l = MSDPTR_L (b_l);
   msdptrs_l = MSDPTR_L (a_l);
  }
 else
  {
   r_l = LSDPTR_L (a_l);
   s_l = LSDPTR_L (b_l);
   msdptrr_l = MSDPTR_L (a_l);
   msdptrs_l = MSDPTR_L (b_l);
  }

 t_l = LSDPTR_L (d_l);
 SETDIGITS_L (d_l, DIGITS_L (r_l - 1));

while (s_l <= msdptrs_l)
 {
  *t_l++ = *r_l++ ^ *s_l++;
 }

while (r_l <= msdptrr_l)
 {
  *t_l++ = *r_l++;
 }
cpy_l (c_l, d_l);
}

The function and_l() can be used to reduce a number a modulo a power of two 2^k by setting a CLINT variable a_l to the value a, a CLINT variable b_l to the value 2^k − 1, and executing and_l(a_l, b_l, c_l). However, this operation executes faster with the function mod2_l() created for this purpose, which takes into account that the binary representation of 2^k − 1 consists exclusively of ones (see Section 4.3).

Occasionally, it is useful to be able to access individual binary digits of a number in order to read or change them. As an example of this we might mention the initialization of a CLINT object as a power of 2, which can be accomplished easily by setting a single bit.

In the following we shall develop three functions, setbit_l(), testbit_l(), and clearbit_l(), which set an individual bit, test a particular bit, and delete a single bit. The functions setbit_l() and clearbit_l() each return the state of the specified bit before the operation. The bit positions are counted from 0, and thus the specified positions can be understood as logarithms of powers of two: If n_l is equal to 0, then setbit_l(n_l, 0) returns the value 0, and afterwards, n_l has the value 2⁰= 1; after a call to setbit_l(n_l, 512), n_l has the value 2⁵¹².

int
setbit_l (CLINT a_l, unsigned int pos)
{
 int res = 0;
 unsigned int i;
 USHORT shorts = (USHORT)(pos >> LDBITPERDGT);
 USHORT bitpos = (USHORT)(pos & (BITPERDGT - 1));
 USHORT m = 1U << bitpos;

 if (pos >= CLINTMAXBIT)
  {
   return E_CLINT_OFL;
  }
 if (shorts >= DIGITS_L (a_l))
  {

for (i = DIGITS_L (a_l) + 1; i <= shorts + 1; i++)
  {
   a_l[i] = 0;
  }
 SETDIGITS_L (a_l, shorts + 1);
}

if (a_l[shorts + 1] & m)
  {
   res = 1;
  }
 a_l[shorts + 1] |= m;
 return res;
}

int
testbit_l (CLINT a_l, unsigned int pos)
{
 int res = 0;
 USHORT shorts = (USHORT)(pos >> LDBITPERDGT);
 USHORT bitpos = (USHORT)(pos & (BITPERDGT - 1));
 if (shorts < DIGITS_L (a_l))
  {
   if (a_l[shorts + 1] & (USHORT)(1U << bitpos))
    res = 1;
  }
 return res;
}

int
clearbit_l (CLINT a_l, unsigned int pos)
{
 int res = 0;
 USHORT shorts = (USHORT)(pos >> LDBITPERDGT);
 USHORT bitpos = (USHORT)(pos & (BITPERDGT - 1));
 USHORT m = 1U << bitpos;

 if (shorts < DIGITS_L (a_l))
  {

if (a_l[shorts + 1] & m)
    {
     res = 1;
    }
   a_l[shorts + 1] &= (USHORT)(~m);
   RMLDZRS_L (a_l);
  }
 return res;
}

Every program requires the ability to make assertions about the equality or inequality or the size relationship of arithmetic variables, and this holds as well for our dealings with CLINT objects. Here, too, the principle is obeyed that the programmer does not need knowledge of the internal structure of the CLINT type, and the determination of how two CLINT objects are related to each other is left to functions designed for such purposes.

The primary function that accomplishes these tasks is the function cmp_l(). It determines which of the relations a_l < b_l, a_l == b_l, or a_l > b_l holds for two CLINT values a_l and b_l. To this end, first the numbers of digits of the CLINT objects, which have been liberated from any leading zeros, are compared. If the number of digits of the operands is the same, then the process begins with a comparison of the most-significant digits; as soon as a difference is detected, the comparison is terminated.

int
cmp_l (CLINT a_l, CLINT b_l)
{
 clint *msdptra_l, *msdptrb_l;
 int la = DIGITS_L (a_l);
 int lb = DIGITS_L (b_l);

if (la == 0 && lb == 0)
 {
  return 0;
 }
while (a_l[la] == 0 && la > 0)
 {
  --la;
 }
while (b_l[lb] == 0 && lb > 0)
 {
  --lb;
 }
if (la == 0 && lb == 0)
 {
  return 0;
 }
if (la > lb)
 {
  return 1;
 }

if (la < lb)
 {
  return −1;
 }

msdptra_l = a_l + la;
msdptrb_l = b_l + lb;

while ((*msdptra_l == *msdptrb_l) && (msdptra_l > a_l))
 {
  msdptra_l--;
  msdptrb_l--;
 }

if (msdptra_l == a_l)
 {
  return 0;
 }
if (*msdptra_l > *msdptrb_l)
 {
  return 1;
 }
else
 {
  return −1;
 }
}

If we are interested in the equality of two CLINT values, then the application of the function cmp_l() is a bit more than is necessary. In this case there is a simpler variant, which avoids the size comparison.

int
equ_l (CLINT a_l, CLINT b_l)
{
 clint *msdptra_l, *msdptrb_l;
 int la = DIGITS_L (a_l);
 int lb = DIGITS_L (b_l);
 if (la == 0 && lb == 0)
  {
   return 1;
  }
 while (a_l[la] == 0 && la > 0)
  {
   --la;
  }
 while (b_l[lb] == 0 && lb > 0)
  {
   --lb;
  }
 if (la == 0 && lb == 0)
  {
   return 1;
  }
 if (la != lb)
  {
   return 0;
  }
 msdptra_l = a_l + la;
 msdptrb_l = b_l + lb;

while ((*msdptra_l == *msdptrb_l) && (msdptra_l > a_l))
  {
   msdptra_l--;
   msdptrb_l--;
  }

 return (msdptra_l > a_l ? 0 : 1);
}

These two functions in their raw form can easily lead the user into the thickets of error. In particular, the meaning of the function values of cmp_l() must be kept constantly in mind or looked up repeatedly. As a measure against errors a number of macros have been created by means of which comparisons can be formulated in a more mnemonically satisfactory way (see in this regard Appendix C, "Macros with Parameters"). For example, we have the following macros, where we equate the objects a_l and b_l with the values they represent:

GE_L (a_l, b_l)     returns 1 if a_l ≥ b_l, and 0 otherwise;
EQZ_L (a_l)      returns 1 if a_l == 0, and 0 if a_l > 0.