I’ll close this chapter with a few miscellaneous observations. First, note that I’m assuming throughout this part of the book (as indeed I did in the previous part as well) that the only dependencies we care about are ones that have to do with projection as the decomposition operator and join as the corresponding recomposition operator. Under that assumption, it’s immediate from the definition of join dependency that JDs are, in a sense, the “ultimate” kind of dependency; that is, there’s no “higher” kind of dependency such that JDs are just a special case of that higher kind. And it follows further that—though I haven’t really defined it properly yet!—fifth normal form is the final normal form[98] with respect to projection and join (which accounts for its alternative name, projection-join normal form).
Second, I’ve referred several times to relvars that are in BCNF and not 5NF; indeed, I’ve tacitly assumed that if relvar R is in 5NF, then it’s certainly in BCNF. In fact this assumption is correct. Let me also state explicitly for the record that 5NF is always achievable; that is, any relvar not in 5NF can always be decomposed into a set of 5NF projections—though not necessarily without losing dependencies, of course, since we already know from Chapter 7 that decomposition to BCNF and preserving dependencies can be conflicting objectives.
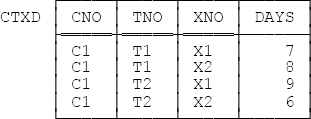
Third, it follows from the definition of 5NF that a relvar R that’s in 5NF is guaranteed to be free of redundancies that can be removed by taking projections. In other words, to say R is in 5NF is to say that further nonloss decomposition of R into projections, while it might be possible, certainly won’t remove any redundancies. Note very carefully, however, that to say R is in 5NF is not to say R is free of redundancy. (A belief to the contrary is another popular misconception. See Exercise 1.11 in Chapter 1.) The fact is, there are many kinds of redundancy that projection as such is powerless to remove—which is an illustration of the point I made in Chapter 1, in the section THE PLACE OF DESIGN THEORY, to the effect that there are numerous issues that current design theory simply doesn’t address at all. By way of example, consider Figure 9-3 below, which shows a sample value for a relvar, CTXD, that’s in 5NF and yet suffers from redundancy. The predicate is Teacher TNO spends DAYS days with textbook XNO on course CNO. The sole key is {CNO,TNO,XNO}. As you can see, the fact that (e.g.) teacher T1 teaches course C1 appears twice, and so does the fact that course C1 uses textbook X1.[99]
Let’s analyze this example a little more carefully:
Since {CNO,TNO,XNO} is a key, the relvar is subject to the following functional dependency—
{ CNO , TNO , XNO } → { DAYS }—which is an “arrow out of a key.”
So DAYS depends on all three of CNO, TNO, and XNO, and it can’t appear in a relvar with anything less than all three.
Hence there’s no (nontrivial) decomposition of the relvar into projections that applies at all—the relvar is in 5NF. Note: A decomposition is trivial if and only if it’s based on dependencies (FDs or JDs) that are themselves trivial in turn, and nontrivial if and only if it isn’t trivial. Trivial FDs were discussed in Chapter 4 and Chapter 5; trivial JDs are discussed in the next chapter.
Hence there’s certainly no decomposition into projections that can remove the redundancies, a fortiori.
[98] Well ... except for 6NF (again, see Chapter 13).
[99] One reviewer argued strongly that those repetitions didn’t really constitute redundancy. Well, I don’t want to argue the point here; I’ll just remind you that I’ll be examining the whole issue of exactly what does constitute redundancy in detail in Chapter 15.