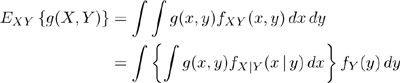As discussed in the preceding chapter, simulation plays an important role in the design of communication systems. Simulation is used for the detailed design of various components in a communication system as well as for system-level performance evaluation. This chapter is, in many ways, a continuation of the material presented in Chapter 1. In this chapter we will consider the modeling and simulation process in more detail and will see that there are both qualitative and quantitative aspects of simulation. Stated another way, simulation is both an art and a science.
Some steps used for creating and executing a simulation model are theoretically based and therefore quantitative in nature. Modeling of individual system components and the generation of random numbers fall in this category. On the other hand, many steps in simulation involve approaches and considerations that are not clearly quantifiable and are heuristic in nature. These are lumped into what is loosely called the “methodology” of simulation. The emphasis of this chapter is on the methodology or the “art” of simulation, especially as it applies to system-level performance evaluation. The “science” of simulation, the part that deals with the quantitative aspects of modeling, estimation, etc., are dealt with in later chapters. The quantitative and qualitative parts of simulation are not totally dichotomous but are closely interrelated. All steps used in simulation, including the modeling of specific components, involve some “methodology”. Furthermore, the executation of a simulation requires a set of algorithms.
For discussion and presentation purposes we will treat these two topics, the quantitative and qualitative aspects of simulation, as if they are somewhat disjoint. However, some familiarity with each topic will aid in the understanding of the other. This chapter should therefore be read before proceeding to the remainder of the book. The material in this chapter will have greatest value, however, if it is periodically revisited as the remaining chapters are studied.
All but the most simple simulation problems involve the following fundamental steps:
Mapping a given problem into a simulation model
Decomposing the overall problem into a set of smaller problems
Selecting an appropriate set of modeling, simulation, and estimation techniques and applying them to solve these subproblems
Combining the results of the subproblems to provide a solution to the overall problem
Usually, specific techniques for solving the smaller subproblems (the third bullet) will be well defined and rigorous, and are algorithmic or quantitative in nature. For example, the technique for simulating a linear filter represented by a transfer function using the finite impulse response (FIR) method is the well-defined convolutional sum. On the other hand, the overall “methodology” used for mapping a design or performance estimation problem to a suitable simulation model, and selecting a set of consistent and compatible techniques for applying that model, will involve heuristic procedures and “tricks of the trade.”
The basic purpose of a communication system is to process waveforms and symbols, and hence the simulation of communication systems is an attempt to emulate this process by generating and processing sampled values of those waveforms. This involves modeling the signal-processing operations performed by the various functional “blocks” in a communication system and generating the required input waveforms that enter the communication system at various points. The process of “running” or “executing” a simulation consists of driving the models with appropriate input waveforms to produce output waveforms (which might serve as inputs to other functional blocks), and analyzing these waveforms to optimize design parameters or to obtain performance measures such as error rates in a digital communication system.
To illustrate the various aspects of methodology, we will use the example of a digital communication system operating over a time-varying or “fading” mobile communication channel. This channel introduces linear distortion that can be minimized by an equalizer in the receiver. The approaches to the detailed design of the equalizer will be used to illustrate some aspects of methodology. The channel will also be time-varying because of mobility, causing the received signal to change randomly as a function of time. This random change in the received signal level is referred to as fading. When the received signal power falls below some threshold, the performance of the system as measured by the probability of error will become unacceptable and the system will be declared to be out of service. The outage probability of a communication system is defined as the percentage of time the communication system is “not available” due to bad channel conditions, which cause the error rate to exceed some specified threshold value. Estimation of the outage probability will require the simulation of the system under a large number of channel conditions and hence is a computationally intensive task. Methods for minimizing the overall computational burden associated with executing the simulation will be discussed.
The overall approach to waveform-level simulation of communication system is straightforward. We start with a description of the portion of the system that is to be simulated in a block diagram form in which each functional block in the block diagram performs a specific signal-processing operation. The appropriate simulation model for each functional block is chosen from a library of available models, and the block diagram model is created by interconnecting the set of chosen blocks (i.e., their models). Specific values, or a permissible range of values, for the parameters of each block, such as the bandwidths of filters, are specified prior to the execution of simulation. The block diagram is simplified if possible, and partitioned if necessary. The mapping of the design, and/or the performance estimation problem, into a simulation model is one of the most difficult steps in methodology. The computer time required for executing the simulation, and the accuracy of the simulation results, will depend upon how well this is done.
The next step involves the generation of sampled values of all the input waveforms or the stimuli to drive the simulation model. Signals, noise, and interference are represented by random processes, and sampled values of random processes are generated using random number generators. During simulation, the outputs of the random number generators are applied as inputs of the appropriate blocks to “drive” the simulation model and produce sampled values at the outputs of various functional blocks. Some of the output samples are recorded and are analyzed either while the simulation is executing (“in-line estimation”) or at the end of simulation (“off-line estimation” or postprocessing), and various performance measures such as signal-to-noise ratios (SNRs), mean-square error, and probability of error are estimated.
The final step, and a very important step, in the simulation is the validation of the simulation results using analytical approximations and bounds, or measured results when available. Measured results are typically available only toward the end of a design cycle after prototypes have been built. Even when a prototype system is available, only a limited number of measurements are typically made. Measurements are inherently expensive and the reason we rely on simulation is to avoid the time and expense of taking a large number of measurements. (If everything can be measured at the time the measurement is required, then there is no need for simulation!) Nevertheless, some validation against measured results has to be done to verify the models and the methodology used, and to establish the credibility of the simulation results.
A real communication system will usually be far too complex to model and simulate exactly in its entirety even if unlimited computational resources are available. A variety of techniques are used to reduce the overall complexity of the simulation problem to something that is within the scope of the available computer resources, the time available, and the accuracy desired. These techniques or tricks of the trade are loosely referred to as methodology and are described in the following sections with examples.
The overall approach, or methodology, used to solve a design or performance estimation problem depends on the nature of the specific problem. While it is difficult to present methodology as an independent set of rules or algorithms, there are certain generic aspects of methodology that can be applied to a wide variety of simulation problems. We describe these first and then present a set of specific methods for solving a set of individual problems.
The starting point of a simulation is a clear statement of the problem and the objectives of the simulation. To illustrate various aspects of methodology, we will use the mobile communication system example, and consider the following two problems:
Equalizer Design: Determine the number of taps, the tap spacing, and the number of bits used to perform the arithmetic operations in the equalizer to be used in the receiver.
System Performance Evaluation: Determine the Eb/N0 required to maintain an acceptable level of performance. (A more detailed description of the system and its performance specifications will be provided in later sections of this chapter.)
The first problem deals with the detailed design of a component in the receiver, whereas the second problem is one of system-level performance estimation. These two problems require different approaches in terms of what portion of the system to model, the level of detail to be included in the model, as well as the modeling techniques, the simulation techniques, and the estimation procedures to be used. Also, we must assume that the first problem has been solved before we can approach the second problem.
Irrespective of whether we are dealing with a detailed design problem, or a high-level performance estimation problem, the starting point is usually a detailed block diagram that represents the portion of the system that needs to be simulated. This block diagram representation, in its initial form, will often include more detail than what might ultimately be necessary and also might have a lot of detail dealing with aspects of the system that might have no bearing on the design or performance issues being addressed. Nevertheless, it is customary and useful, as a starting point, to include “everything that one can think of” in the initial overall block diagram.
The final simulation model is created from the initial block diagram by simplifying it. There are three classes of generic techniques that are applied in this step of creating a simulation model:
Hierarchical representation
Partitioning and conditioning
Simplifications (approximations, assumptions, and various simplifications)
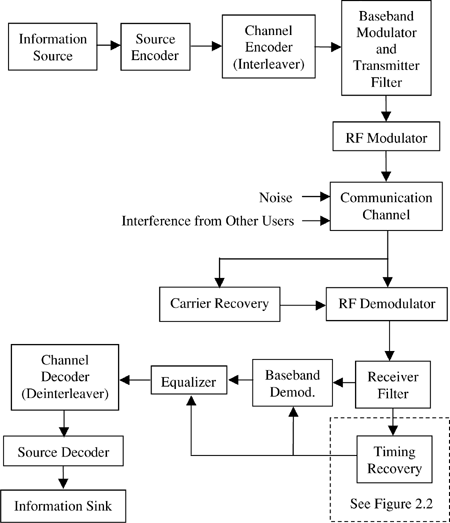
Hierarchy is a commonly used approach for reducing the complexity in modeling, software design and other applications. In the context of a communication system, hierarchy is used to manage and reduce the complexity of the simulation model and also reduce the computational load associated with simulating the model. The hierarchical representation is done in various “layers” starting with a “system”-level model and progressing down through various other layers, which are usually referred to as the subsystem layer, the component layer, and the physical (gate-level or circuit) layer. Example “layers” for a particular communications system are shown in Figures 2.1, 2.2, and 2.3. The number of layers and the terminology used to define a given layer are not unique. There could be an arbitrary number of layers in the hierarchy, and what might be viewed as a subsystem in one context may be considered as a system in a different context. Nevertheless, we will use the term system to refer to the entire entity of interest. In terms of a hardware analogy, a system usually may be viewed as what is contained in a rack, cabinet, or box. A system contains subsystems that are often implemented at the board level. Boards are assembled from components (discrete components and ICs) and what is inside ICs are transistors and other physical devices.
In a hierarchical representation, or model of a system, the building blocks used in lower layers in the hierarchy will contain more detail, whereas the blocks at the higher layers are more abstract and deal with the overall function of the block. The decomposition into lower layers is done until no further meaningful decomposition is possible or necessary. The lowest level is often based on components such as resistors, capacitors, and ICs.
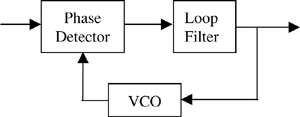
In the context of a communication system, the system-level model, shown in Figure 2.1, will consist of functional blocks such as information sources, encoders, decoders, modulators, demodulators, filters, and the channel. Each of these functional blocks can be considered a subsystem and decomposed, or expanded further, in order to show more detail. For example, the timing recovery subsystem can be decomposed into a fourth-order nonlinearity, two bandpass filters, and a phase-locked loop (PLL) as shown in Figure 2.2. Additional decomposition yields a “component”-level model. As examples, the bandpass filters shown in Figure 2.2 may be discrete component analog filters, microwave filters, or digital filters. In the case of analog filters, it might be possible to expand the filters into “circuit”-level models. For a digital filter, this decomposition will be down to bit-level adders, multipliers, and accumulators. A layer below this will involve individual transistors and gates. However, we very seldom go down to this level of detail in the context of waveform-level simulation of communication systems. The “component”-layer model for the PLL, which was briefly discussed in Chapter 1, is shown in Figure 2.3. We will consider the simulation of the PLL in detail later in this book. As with the filter, additional decomposition to a circuit-level model may be necessary for certain applications.
The main reason for using the concept of hierarchy is to manage the complexity of the simulation model and also to reduce the computational burden associated with simulating the model. In general, one should perform the simulation at the highest possible level of abstraction, consistent with the goals of the simulation, since higher levels of abstraction imply fewer paramerers and more efficient simulations. In the equalizer design example, the equalizer itself might be simulated at the bit level, whereas the channel might be simulated at a much higher level of abstraction. For example, a transfer function might be used to represent a channel. Similarly, a digital baseband filter in the receiver need not be simulated at the bit level if the goal of the simulation is system performance evaluation. The manner in which the filter is implemented will, of course, not affect the performance of the overall system so long as the transfer function of the filter is preserved.
In addition to reducing complexity and the required simulation time, higher-level models will have fewer parameters and also might be easier to validate. Fewer parameters imply that the model can be characterized by fewer measurements. For example, a circuit-level model of a Butterworth filter might involve a dozen or more component values. However, a high-level transfer function of the same Butterworth filter is characterized by just two parameters, the filter order and the filter bandwidth. Both of these parameters are easy to measure. In addition, validation of simulation results is simpler, with fewer measurements required, when the simulation model is at a higher level of abstraction.
At the system level, simulation is done at a highest level of abstraction using “behavioral” models such as transfer functions rather than physical models. The functional forms of the behavioral models are usually assumed or obtained from separate, but not concurrent, simulations of the lower-level blocks, or from measurements. A digital filter, for example, might be simulated at the bit level and an analog filter might be simulated at the circuit level. A higher-level model for both filters can be derived from the bit-level or circuit-level simulations in the form of a transfer function. The only model for the filter that will be used at the higher level will be the transfer function model, which is computationally more efficient than a bit-level or circuit-level model. The details of the lower-level model, whether it is an analog filter or digital filter, is completely hidden from the higher layer. This approach of creating a higher-level model from the details of a lower-level model, and substituting back at the higher level is called “back annotation.”
During the early phase of the design cycle, the filter transfer function is assumed or “specified” (e.g., a fifth-order Elliptic filter) and the actual characterization of the transfer function will be obtained later when the filter has been designed and simulated. Later in the design cycle, when the filter is actually built, its transfer function can be measured and the measured transfer function can be used in higher-level simulations. Simulation is very flexible in this context and a hierarchical approach adds to the flexibility of including multiple versions of models for a subsystem or a component with different levels of abstraction, but with the same external interfaces and parameters. In addition, hierarchy also reduces overall model complexity and the resulting computational burden.
Like the modeling process, the actual design of a communication system also flows top down through various layers. In the design process, specifications flow down through the layers of the hierarchy, and characterization (measured or simulated at the lower levels) flows back up through the layers of hierarchy. In some applications, it might be necessary to use different levels of detail in a single simulation model. For example, in the equalizer design, it may be necessary to estimate the system probability of error as a function of number of bits used for arithmetic in the equalizer. In this case all parts of the system surrounding the equalizer will be simulated at a very high level of abstraction, whereas the equalizer itself might be simulated in great detail using, sometimes, a different simulator. This approach is often referred to as “co-simulation.”
Partitioning of a complex problem into a set of interrelated but independent problems, which can be solved separately and whose solutions can be combined later, is another technique that is useful for reducing the complexity and also the computational burden. Whereas hierarchy deals with different levels of abstraction, partitioning usually deals with the same level of abstraction but with various aspects of the problem that can be simulated separately and the results combined. Thus, for partitioning, we view and inspect the block diagram “horizontally” while hierarchy may be viewed as a “vertical” separation. In the context of the example shown in Figure 2.1 it might be possible to separate synchronization and coding from the rest of the problem and simulate them separately.
Conditioning is another technique that is very similar to partitioning—we simply fix the condition or state of a portion of the system and simulate the rest of the system under various values of the conditioned variables or states. The conditioned part of the system is simulated separately and the results obtained in the first part are averaged with respect to the distribution of the conditioning variable obtained in the second part. This process is best illustrated with an example.
Suppose we wish to estimate the probability of error in the system shown in Figure 2.1 with nonideal synchronization (timing and carrier recovery). We can use partitioning and conditioning to simplify the problem by estimating the conditional probability of error in the system for various values of timing and carrier phase errors, and then simulating the synchronization system to obtain the distribution of the timing errors. We then average the conditional probability of error with respect to the distribution of timing errors and phase errors. What we are doing here is a well-known operation in statistics involving conditional expected values. In general:
which, in terms of conditional expectation, is
Returning to our example of determining the bit error rate (BER) in the presence of timing errors and phase errors, this principle can be applied to give
where ![]() is the simulation-based estimate of the conditioned probability of error in the system given that the phase error is θ and the timing error is τ. The result of averaging,
is the simulation-based estimate of the conditioned probability of error in the system given that the phase error is θ and the timing error is τ. The result of averaging, ![]() , is the unconditioned (overall) probability of error and ƒTΘ(τ,θ) is the estimated (simulated) distribution of the phase error and timing error produced by the synchronization system. Note that the synchronization system is simulated by itself, apart from the rest of the system, and the results are averaged. This leads to the simulation of two simpler systems and should result in less simulation time.
, is the unconditioned (overall) probability of error and ƒTΘ(τ,θ) is the estimated (simulated) distribution of the phase error and timing error produced by the synchronization system. Note that the synchronization system is simulated by itself, apart from the rest of the system, and the results are averaged. This leads to the simulation of two simpler systems and should result in less simulation time.
If we can assume that the timing and phase recovery systems produce independent timing and phase errors, then these parts can be partitioned and simulated separately to obtain estimates of the distributions of the timing error, ![]() , and the phase error,
, and the phase error, ![]() . The joint distribution of the timing and phase error can be obtained as
. The joint distribution of the timing and phase error can be obtained as
which can then be substituted in (2.3) to do the averaging.
It should be noted that partitioning deals with separating the problem into parts and conditioning guides partitioning and, more importantly, helps integrate the results. The independence assumption, where appropriate, also aids in bringing simulation results together. The latter will be case in which the simulated parts produce statistically independent phenomena and processes that need to be combined.
It was stated earlier that, as a starting point, it is common practice to include as much detail in the initial block diagram model as possible. The complexities of the overall model and the subsystem models are then reduced using a number of techniques including the omission of those blocks that do not have a significant impact on the problem being addressed, the use of approximations, and simplification by combining blocks.
As an example of how portions of the block diagram may be omitted, consider the system-level performance evaluation problem. If we can assume that the channel is very slowly time varying, and that the system is operating at a high signal-to-noise ratio, S/N, it is reasonable to expect that synchronization errors will be very small and hence the effects of synchronization can be ignored during performance estimation. In this situation, the timing recovery and the carrier recovery portions need not be simulated and can be deleted from the block diagram.
Approximations and assumptions are used extensively to simplify the simulation model. The most commonly used assumptions and approximations involve time invariance (stationarity), and linearization. While most practical systems, when observed over a long time and over a wide dynamic range of the input signal, might exhibit time-varying and nonlinear behavior, they can be well approximated by linear and time-invariant models over short time periods and for low signal levels.
Time invariance implies that over the simulation interval, the properties of the signals and system components being modeled do not change. In practice, the concept of time invariance is applied as an approximation in a relative and not in an absolute sense. If a system parameter is changing slowly, there are situations in which it may be assumed fixed over the simulation interval. As an example, consider the problem of BER estimation over a radio channel in which the transmit and receive antennas are stationary. If the changes in channel characteristics are due to changes in the atmospheric conditions, which have a time constant of several minutes to hours, and if the symbol rate of transmission is millions of symbols per second, then the channel can be assumed to be “quasi-static”. That is to say that the channel remains in nearly the same condition while several hundred millions of symbols flow through it and it is meaningful to talk about instantaneous probability of error for a given channel condition. If the BER being estimated is of the order of 10−3, then we need to simulate only a few thousand symbols to estimate this BER. This represents a simulation time interval of milliseconds, whereas the time constant of the channel is of the order of several minutes and hence it is reasonable to assume the channel to be static during the simulation interval. This quasi-static approximation plays a very important role in simplifying simulation models.
The quasi-static assumption, and the resulting simplifications, may be applied in any system in which we have phenomena and processes that have significantly different bandwidths. In such systems, it might be possible to simulate the effects of the faster process while assuming the slow process to be in a fixed state. We can therefore view the quasi-static assumption as a requirement for partitioning and conditioning.
In a similar vein, we use linear approximations for nonlinear components. Nonlinear models in general are very complex to analyze, and while they are somewhat easier to simulate, they still pose problems. Whenever possible we try to approximate the behavior of these components by linear models.
Finally, we use many of the principles of linear systems to simplify the block diagram. We can combine several cascaded and parallel blocks into one block by multiplying or adding the transfer functions of the cascaded and parallel blocks, respectively. In the case of linear time-invariant blocks we can also interchange the order of the blocks when doing so leads to a simpler model. This type of simplification is desirable, especially when using simulation for performance estimation. First of all, performance estimation simulations are usually very long, and hence the effort in simplifying the model is justifiable. Second, unlike the situation in which simulation is used to support a detailed design, we are not interested in observing the evolution and progression of waveform through each functional block of the system. When simulation is used for performance estimation we are usually interested in simply comparing the input and output waveforms and counting errors. In this situation the intermediate waveforms are of very little interest or use. The entire system can be reduced to a very small number of blocks during performance estimation, and this would lead to considerable reduction in simulation time. If the blocks have similar complexity, combining the transfer function of n blocks will lead to computational savings of the order of (but less than) n.
To state the obvious, it must be clear that every attempt should be made to reduce the simulation model to the smallest number of functional blocks possible with the highest-level abstraction consistent with the goals of the simulation exercise. High-level models and lower-level models are relative terms. While high-level system descriptions with a smaller number of subsystem models will require less computation time, more detailed models will in general lead to more accurate simulation results. This improved accuracy, however, comes at the expense of increased computational time.
The role of each functional block in a communication system is to perform a specific signal-processing function and hence its simulation model should mirror this function with varying degrees of abstraction. Irrespective of the internal details, the simulation model should accept a sequence of time-ordered samples of the input waveform and produce a time-ordered set of output samples according to some well-defined transfer characteristic. A number of choices and considerations must be taken into account in building the model, and we describe some of the methodological issues associated with modeling in the following sections. (Even though we now focus our attention on models at the system or subsystem level, some of the methodological issues described in the preceding section apply here. Also, many of the concepts described here at the subsystem level also apply at the system level.)
The simulation model of a subsystem or a component (block) is a transformation of the form
where x [k] represents input samples, y[k] represents output samples, p1,p2, ..., pq represent parameters of the block, and k = m, 2m, 3m, ... is a time index. The model uses n samples of the input to produce m samples of the output per “invocation” of the model according to the transformation F, which will be defined explicitly in terms of the input samples, the parameters of the block, and the time index k. If the transformation F does not depend upon the index k, the model is time invariant. If m > 0, the model is considered a block input-output model, and when m = 0 we have a sample-by-sample model. If n = 0 the model is memoryless.
In constructing the model for a functional block, and executing the model within a simulation, a number of considerations must be taken into account. These considerations are related to each other even though they are presented in an arbitrary order.
Communication systems contain components and signals that are either bandpass or lowpass in nature. From a simulation perspective, it is computationally advantageous to represent all signals and system elements by the complex lowpass equivalent representation. For signals and linear systems, the lowpass equivalent is obtained by shifting the bandpass spectra from the carrier frequency to f = 0 and the linear model of the block can be implemented using the lowpass equivalent representation of the input and output signals and the signal transformation. Details of this representation are presented in Chapter 4.
The lowpass equivalent of a deterministic signal is obtained via frequency translation of its Fourier transform, whereas the power spectral densities are used for random signals. If the bandpass spectrum is nonsymmetric around the carrier, the lowpass equivalent representation in the time domain will be complex valued. Furthermore, the components of the lowpass equivalent random process will be correlated in this case.
For certain types of nonlinear systems it is also possible to use the lowpass equivalent representation. Details of the lowpass equivalent models for nonlinear systems are described in Chapter 12.
When signals and systems are lowpass or represented by their lowpass equivalent in the bandpass case, they can be sampled and represented by uniformly time spaced samples. The minimum sampling rate required is twice the bandwidth of the signal (or the system) for the ideal lowpass case. However, in practical cases in which frequency functions may not be confined to a finite bandwidth, the sampling rate is often taken to be 8 to 16 times some measure of bandwidth, such as the 3-dB bandwidth. In the case of digital systems the sampling rate is usually set at 8 to 16 times the symbol rate. Factors such as aliasing error, frequency warping in filters implemented using bilinear transforms, and bandwidth expansion due to nonlinearities need to be considered in establishing a suitable sampling rate. These effects can be minimized by increasing the sampling rate, but higher sampling rates will increase the computational load and therefore one has to trade off accuracy versus simulation time. Multirate sampling, variable step size, and/or partitioning fast and slower parts of the system, when possible, are techniques that can be applied to reduce the computational burden.
While most of the blocks in communication systems will be linear, a significant portion of a communication system may involve nonlinear processing. Some of the nonlinear processing is intentional whereas some is unintended. Examples of the former are operations such as decision feedback equalizers, nonlinear operations in synchronization subsystems, and intentional limiting of impulse noise. Examples of the latter are the nonlinear behavior of power amplifiers near their maximum operating power.
As a first approximation, most of the nonlinearities can be modeled as having linear effects on communication signals, particularly if the signal is a constant envelope signal such as phase-shift keying (PSK). However, in multicarrier systems, or in single-carrier systems with higher-order quadrature amplitude modulation (QAM), unintended nonlinear behavior might impact system performance significantly and hence it is necessary to include nonlinear simulation models. Fortunately, most of these nonlinearities in communication systems can be modeled efficiently using complex lowpass equivalent representation.
There are various approaches to modeling systems with nonlinearities. These include, in order of increasing complexity, memoryless power series nonlinear models, frequency-selective nonlinear models with memory, and nonlinear differential equations. The mathematical analysis of nonlinear systems, and the evaluation of the effects of nonlinearities, is in general difficult. However, simulation is rather straightforward even in the case of frequency-selective nonlinear models.
Nonlinear models fall into two broad categories: input-output block models and nonlinear differential equations. The first set of models are usually based on measurements whereas the second class of models are often derived from modeling the physical behavior of the device. Solutions of nonlinear differential equation models implemented using variable time-step integration models are computationally most efficient even though they might involve more setup time. It is also possible to decompose a nonlinear subsystem in a block diagram form and simulate in block diagram form using simpler building blocks such as memoryless nonlinearities and filters. This approach, although easier to set up, will not be the most computationally efficient approach.
One important factor that must be considered while simulating nonlinear elements is that the nonlinearity will produce bandwidth expansion and the sampling rate has to be set high enough to capture the effects of the bandwidth expansion.
As stated earlier, all systems, components, and processes will exhibit time-varying behavior to some extent when observed over a long time period. Whether or not to use a time-varying model is guided by a number of factors.
In many applications such as modeling and simulating an optical fiber, the fiber characteristics may change very little over the lifespan of the communication system, and hence a time-invariant model will be adequate. In other cases, the time variations might be significant but the rate of change of the time variations may be very slow compared to the bandwidth of the time-invariant parts of the system. The quasi-static approximation is valid in this situation and the simulation can be carried out using fixed snapshots of the time-varying parts and the results can be averaged (i.e., partitioning and averaging). In these two cases, the performance measure of interest is some long-term average rather than the dynamic behavior.
The third approach that is warranted sometimes is the dynamic simulation of the time variations. This approach is used when the time variations are “rapid” and the performance measure of interest is based on the dynamic or transient behavior of the system is of interest. An example of this is the acquisition and tracking behavior of the synchronization subsystem time in a burst mode communication system operating over a fast fading channel. The simulation model for this case will be a tapped delay line with time-varying tap gains, which are often modeled as filtered random processes.
While the tapped delay line simulation model for time-varying systems is straightforward to derive and implement, two factors must be taken into account. First, there might be significant spectral spreading due to time variations. The result of this spectral spreading will lead to a requirement for higher sampling rates. In addition, the order of time-varying blocks cannot be changed, since the commutative property does not hold for time-varying systems.
If the instantaneous output y[k] of a component depends on the instantaneous input x[k] (or x[k − j]), the component is memoryless; otherwise the component has memory. Filters, due to their frequency-selective behavior, have memory (frequency-selective behavior and memory are synonymous). Also, some types of nonlinearities have memory and there are many models available for simulating such components. Care must be exercised in implementing models with memory with respect to storing the internal states of the model such that the model can be reentrant. For example, when a generic filter model is used in several instances in a block diagram, the internal state of each instance of the filter must be stored separately so that when a filter model is invoked several times during a simulation it is always entered with its previous state intact.
The input-output relationship of a functional block, or system component, can be modeled and simulated in either the time domain or in the frequency domain. The computational burden of the two approaches for linear blocks is often approximately equivalent,[1] and the preferred domain of implementation will depend on the domain in which the specifications are initially provided. For example, if a filter is specified in terms of measured frequency response, it is natural and convenient to implement the filtering operation within the model in frequency domain. For nonlinear components, the specifications and implementation are almost always performed in the time domain.
While the implementation of a model can be in either the time or frequency domain, it is common practice to use time domain samples to represent the input and output signals. Frequency domain models, such as filters simulated using the fast Fourier transform (FFT), will require internal buffering of the time domain input samples, taking the transform of the input vector stored in the buffer followed by frequency domain processing, inverse FFT, and buffering at the output. Buffering is required, since taking the transform is a block-processing operation based on a set of samples rather than on a single sample. During simulation, samples of the input and output may be transferred in and out of the buffers one sample at a time or in blocks of N samples.
A model may be implemented to accept and process one time domain sample at a time or a block of N time domain samples per invocation of the model. The computational efficiency of the two methods will depend on the relative complexity of the model and the overhead associated with the invocation of the model. If the model is simple with a small number of internal states and parameters, or if the overhead of calling or invoking a model is small compared to the computations performed inside the model, then it is convenient and efficient to invoke the model on a sample-by-sample basis. When the invocation overhead is large, it is computationally more efficient to use a block or vector-processing approach where the model is called with an input vector of size N.
Block processing requires buffering and a careful interface to the blocks preceding and following the block in question. Block processing introduces a time delay of N * Ts seconds, since the output cannot be computed until all N samples of the input are accumulated and transferred into the model. Inclusion of a block input-output model in a feedback loop will produce incorrect results because of the large processing delay. Also, if block-processing models are intermixed with nonlinear models, it may be necessary to revert to sample-by-sample processing for the nonlinear elements, since blocking the input and processing on a block-by-block basis assumes that superposition holds, which is not the case with nonlinear blocks. An example of this situation occurs when a nonlinearity appears between two overlap and add type FFT filters. The overlap and add FFT filter is based on the linearity principle. The technique is to compute the filter response to nonoverlapping blocks of input samples and add the responses at the output. With a nonlinearity after the filter, this block processing cannot be carried through the nonlinearity, since superposition does not apply across the nonlinearity. To do this processing correctly, the response due to each block of input samples has to be added at the output of the first filter, and the nonlinearity model then processes the added output of the first filter on a sample-by-sample basis. The output of the nonlinearity can then be processed by the second filter using the overlap and add method of block processing.
Another factor that has to be taken into account with block processing is scheduling. If different models in a system use different input and output block sizes, then the simulation framework should be capable of scheduling the order and frequency of invocations properly. Otherwise, the user has to take care of the scheduling.
Multirate sampling is used in simulations if a system model includes processes and phenomena of widely differing bandwidths. With multirate sampling, each signal is sampled and processed at a rate consistent with its bandwidth, and this leads to significant improvements in computational efficiency. When multirate sampling is used, interpolation and or decimation might be necessary to interface the sample streams with different sampling rates.
Variable step-size processing is also used often to improve computational efficiency. This approach is commonly used in numerical integration routines for solving linear and nonlinear differential equations. If the underlying differential equations and their solutions are well behaved, then this approach will reduce the computational load significantly. When a variable step size is used in a model, the output has to be buffered and resampled if the following blocks use a uniform step size.
One of the primary uses of simulation is design optimization, which in most cases reduces to finding the optimum value of critical parameters such as the bandwidth of a receiver filter, the operating point of an amplifier, and the number of quantization levels to be used in the receiver. In order to do this, models have to parameterized properly and the key design parameters should be made visible externally; that is, models should have “external knobs” that can be used to adjust the deign parameter iteratively during simulations. One consideration that must be taken into account is the number of parameters for a given model. In general this number should be kept to a minimum, since a complex communication system will involve a large number of components. If each component has a large number of external parameters, the overall parameter space becomes very large. In this case it will be extremely difficult to optimize the design using simulation. Also, measurement of parameter values and validation becomes easier with a smaller number of parameters.
While the modeling and simulation approach used for each component depends on the nature of the component being modeled and simulated, considerable attention must be paid to the interfacing of a given model to the models of other blocks. Since the block diagram of a system might consist of an arbitrary set of blocks that are interconnected in an arbitrary manner, consistency and compatibility must be ensured either by the simulation framework and/or by the user. This task can be made easier if the models of individual blocks are constructed with well-defined and well-documented interfaces. Inconsistencies might result for a number of reasons. These include different domains of processing, signal types, block size, step size, multirate sampling, inconsistent parameter specification within different blocks, and many other reasons outlined in the preceding sections.
Many of the difficulties in simulating a complex system-level model arise because of these inconsistencies. Hence it is necessary to exercise care in formulating the overall simulation model and the selection of the individual blocks and their parameters in the context of not only the individual models but also in the context of the overall model.
Assuming that we have a system model with the highest level of abstraction and least complexity, we now turn our attention to aspects of methodology that apply to modeling and generating the input waveforms (signals, noise, and interference) that drive the simulation model. Since the basic goal of waveform-level simulation of communication systems is to emulate the waveforms in the system and compute some measures of waveform fidelity, it is important that close attention be paid to the modeling and simulation of the input waveforms or stimuli.
In a communication systems, information-bearing waveforms as well as unwanted noise and interference are random in nature and they are modeled by random processes. Stationarity is almost universally assumed, since it can be justified in many cases based on the nature of the signals or sequences being modeled. For example, the statistics of the symbol sequence in an English-language text have not changed over hundreds of years and hence a stationary model can be justified.
Stationary random processes are characterized by multidimensional probability distributions, which are difficult to specify, and it is also very difficult in the general case to generate sampled values of a stationary process with an arbitrary n-dimensional distribution. One notable exception is the stationary Gaussian process, which is completely specified by the second-order distribution (whose parameters are the mean and the autocorrelation function). For non-Gaussian processes it is a common practice to limit the specification to second-order distributions.
Sampled values of random processes that are used to drive the simulations are sequences of random numbers that are generated using random number generators. Algorithms for generating random sequences with arbitrary distributions (first and second order) and correlation functions are presented elsewhere in the book. We discuss below some aspects of methodology that apply the modeling and generation of sampled values of random process.
Two concepts simplify the stimuli generation considerably. The first one is the Gaussian approximation, which can be invoked via the central limit theorem, which states that the summed effect due to a large number of independent causes tends to a Gaussian process. In other words, Y = X1 + X2 + ... + Xn approaches a Gaussian distribution for large n assuming that the component variables Xi are independent. Thus, the noise picked up by the antenna of a receiver, contributed by a large number of sources, can be approximated by a Gaussian process. Similarly, interference from a large number of users can also be approximated by a Gaussian process, and hence it is not necessary to individually generate the signals from a large number of users and sum them. The net result can be duplicated by the output of a single Gaussian random number generator.
The second concept deals with the notion of equivalent process representation, which can be stated as follows. Suppose an input random process X(t) goes through n blocks and appears at the output of the nth block as a process Y(t). If by some means (through a rigorous analysis or by approximation or through simulation itself) we can deduce the properties of the process Y(t), then for all subsequent processing that follows the nth block we can simply inject a sequence that represents the sampled values of Y(t), thus eliminating the need to generate and process sampled values of X(t) through n blocks. When X(t) is Gaussian and the blocks are linear it can be shown analytically that Y(t) will also be Gaussian. The parameters of the process Y(t) can be derived analytically or through a simulation of X(t) passing through the n blocks. Unfortunately, it is difficult to derive the properties of Y(t) analytically when X(t) is arbitrary and or the blocks are nonlinear. In such cases simulation can be used to estimate the properties of Y(t) and the estimated properties can be used to generate the equivalent process.
This approach is used to represent phase noise in communication systems as well as timing and phase jitter produced by synchronization subsystems. The most commonly used assumption here is that these processes are stationary Gaussian. For the front-end noise process, the power spectral density (PSD) that will be assumed to be white. For other processes, the PSD is assumed to be given in closed form as a ratio of polynomials in f2, in which case the process can be generated by filtering a white Gaussian process with a filter whose transfer function can be obtained using spectral factorization methods. In the case of arbitrary PSD functions, such as the case for the doppler PSD of fading channels, we can either approximate the spectrum by a ratio of polynomials in f2 and apply the spectral factoring method to obtain the transfer function of a filter or fit an autoregressive moving average (ARMA) model directly to the PSD to obtain the coefficients of a recursive filter that will produce the desired PSD.
Non-Gaussian processes with arbitrary PSDs are harder to synthesize and simulate. A method for handling this case, though very difficult to apply, may be found Chapter 7.
It is not uncommon to have in a communication system many different random phenomena with widely different bandwidths or “time constants”. If the bandwidth of one process is much different from the other, say, a difference of several orders of magnitude, then one of the following two approaches should be taken in order to reduce simulation time. In the first approach, which is applicable when the bandwidths differ by several orders of magnitude, the problem should be partitioned and conditioned on the slow process and the simulation should be executed separately if possible with the value of the slow process held constant while the portion of the system dealing with the faster process is simulated. There is no need to generate sampled values of the slow process during the simulation, since its value will change very little over the duration of a large number of samples of the faster process. This approach is commonly used to simulate the performance of communication systems operating over slowly fading channels.
A second approach that can be considered is multirate sampling, which is applicable when the bandwidths of the processes differ, say, by one or two orders of magnitude. Here the processes are sampled at different rates consistent with their bandwidths so that the number of samples generated during the simulation interval is proportional to the bandwidths of the respective processes. Interpolation and decimation can be used when necessary to mix these signals together at some point in the system. (If the bandwidths differ by less than an order of magnitude, then the overhead associated with multirate sampling will offset any computational savings that might result.)
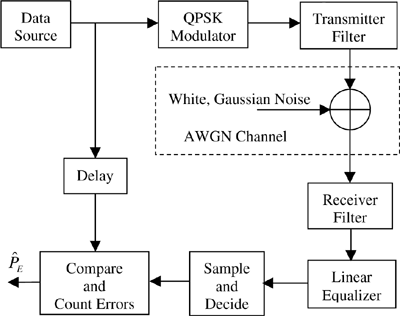
One of the main objectives of simulation is performance estimation. For communication systems, the primary measure of performance is the output signal-to-noise ratio (S/N)o for analog communication systems, and bit error rate (BER) or frame error rate (FER) for digital communication systems. Signal-to-noise ratio is also a secondary measure of performance in digital communication systems. Performance measures are estimated using Monte Carlo techniques. To illustrate the methodology aspects of Monte Carlo simulation and performance estimation, let us consider the problem of estimating the probability of error in a digital communication system. The simulation model for the candidate system in shown in Figure 2.4. Note that the simulation model in this figure is a simplified model of the system shown in Figure 2.1. Some blocks such as the synchronization and coding are left out of this block diagram. Synchronization is either assumed to be ideal, or the effects of imperfect synchronization are handled though conditioning and partitioning as explained in the preceding section. Coding is also omitted, since our focus here is on computing the uncoded probability of error in the system; the effects of coding are handled separately as outlined in Chapter 8. Also, the channel is assumed to be slowly varying or quasi-static, and the equalizer weights are “frozen” in place after they have converged to steady-state values.
The bit error rate performance of the system can be simulated using a random bit sequence as the modulator input and it is not necessary to include an actual data source, source decoder, error control coder, and interleaver in the overall simulation model—the net effect of these blocks is to produce a random binary sequence, and therefore these functional blocks can be omitted from the block diagram and be replaced by a block that produces as its output a random binary sequence.
These simplifications are typical of what is usually done prior to executing a simulation for performance estimation. The primary motivation for the simplification is the reduction of simulation time, which could be very long in the case of performance estimation involving low error rates. Hence, only those components that might have a significant impact on performance are included in the block diagram, which is reduced to as minimal a form as possible.
The BER is determined using the Monte Carlo method. As mentioned in the previous chapter, the bit (or symbol) error probability cannot be determined but rather is estimated by passing N symbols through the system and counting errors. Assuming that Ne errors are counted in passing N symbols through the system, the BER is
which is an estimate of the error probability
In general, the Monte Carlo estimate is unbiased. Small values of N give error estimates with large variance and large values of N give error estimates with small variance. The estimate ![]() converges to PE, the true value of the error probability, as N → ∞, and we therefore typically use the largest practical value of N. A natural tradeoff exists between simulation accuracy and the simulation run time. In a later chapter we consider techniques for reducing the variance of the error estimate for a fixed value of N. These techniques, collectively known as variance reduction techniques, require a combination of analysis and simulation and must be applied with considerable care.
converges to PE, the true value of the error probability, as N → ∞, and we therefore typically use the largest practical value of N. A natural tradeoff exists between simulation accuracy and the simulation run time. In a later chapter we consider techniques for reducing the variance of the error estimate for a fixed value of N. These techniques, collectively known as variance reduction techniques, require a combination of analysis and simulation and must be applied with considerable care.
Two functional blocks appear in the simulation model, Figure 2.4, that are not part of the physical system being analyzed. These are the blocks labeled “Delay” and “Compare and Count Errors”. The “Compare and Count Errors” block has a clear function. The received symbols are compared to the original data symbols so that the error count, Ne, can be determined. A moment’s thought shows the need for the block labeled “Delay”. A number of the functional blocks in the communication system have a nonzero phase response, and therefore a signal passing through these functional blocks incurs a time delay. As a result, the signal at the output of the data source must be delayed so that a given symbol at the output of the receiver is compared to the corresponding symbol at the output of the data source. The determination of this delay must be done with care. If the delay is not exactly correct, the resulting BER estimate will no longer be unbiased and, on average, the estimated BER will exceed the true probability of error. The determination of the appropriate value of the “delay” is part of the important part of a procedure known as calibration. Calibration of a simulation is a procedure performed to ensure that signal levels, noise levels, delays, and other important system attributes in the simulation of a system match the corresponding attributes of the system being simulated. This important aspect of simulation is examined in detail in Chapter 10 when we consider Monte Carlo methods in detail.
The delay block is realized as a delay line of variable length. The length for a specific application is selected to give the proper alignment of demodulated symbols at the receiver output with the symbols at the data source output. The delay is usually quantized to be an integer number of sampling periods. Having very fine control over the delay requires having very short sampling periods or, equivalently, having very large sampling frequency for the simulation. Increasing the sampling frequency increases the required time to execute the simulation. This is a typical result, and we will see in our future studies that minimizing the error sources in a simulation has the negative effect of increasing the simulation run time. Effectively controlling the many tradeoffs involved in developing an effective simulation is, as previously noted, part of the “art” of simulation.
This chapter has presented the basic methodology that is used for simulation development. Whether time driven or event driven, simulations must be properly developed and organized if reliable, and verifiable, results are to be obtained. The concepts presented in this chapter outline the main considerations that play a significant role in this process. The organizational structure of a simulation often mirrors the approach used for actual system design. However, many tricks of the trade have been discussed that can be applied to a simulation in order to ensure that the simulation results accurately reflect the operation of the system under design or evaluation. Throughout the remainder of this book, we will make use of the techniques outlined in this chapter. As pointed out early in this chapter, the student is encouraged to revisit this material from time to time as the study of simulation progresses.
The references given in Chapter 1 are also appropriate for the material given here.
2.1 | Read the table of contents of the two books, Simulation of Communication Systems by Jeruchim, Balaban, and Shanmugan, and Simulation Techniques by Gardner and Baker (citations to these two books are given in the Further Reading section of Chapter 1). Compare the topics covered in these two books with the ones covered in this text. |
2.2 | Read and summarize the following tutorial articles dealing with simulation:
|
2.3 | The IEEE Journal on Selected Areas in Communications periodically publishes issues on computer-aided modeling and analysis of communication systems. Starting with the first issue on this topic, which was published in January 1984, locate all subsequent issues on this topic. Scan the articles in these issues and write a brief paper covering:
|
2.4 | Find the Websites for the following software packages: MATLAB, Labview, SPW, ADS, OPNET, and others. From these Websites download general information about these packages. Collect and summarize information about the following aspects of these packages:
|
2.5 | Consider a passive single-pole RC lowpass filter. Describe the various hierarchical representations of the filter in terms of “layers” as discussed earlier in this chapter. |
2.6 | Describe how conditioning could be used to simulate the impact of timing errors in a matched-filter data detector. |
[1] At first reading this statement may not seem obvious. The computational burden associated with the convolutation required for simulaion of systems with memory in the time domain can be reduced by truncating the impulse response and using an infinite impulse response (IIR) filter structure. Some preprocessing must be done to establish the filter structure but this need only be done once. Overhead is also associated with the frequency domain approach because of the required buffering.