Chapter 16. Parallelization Techniques for Random Number Generators
Thomas Bradley, Jacques du Toit, Robert Tong, Mike Giles and Paul Woodhams
In this chapter, we discuss the parallelization of three very popular random number generators. In each case, the random number sequence that is generated is identical to that produced on a CPU by the standard sequential algorithm. The key to the parallelization is that each CUDA thread block generates a particular block of numbers within the original sequence, and to do this step, it needs an efficient skip-ahead algorithm to jump to the start of its block.
Although the general approach is the same in the three cases, there are significant differences in the details of the implementation owing to differences in the size of the state information required by each generator. This point is perhaps of most general interest, the way in which consideration of the number of registers required, the details of data dependency in advancing the state, and the desire for memory coalescence in storing the output lead to different implementations in the three cases.
16.1. Introduction
Random number generation
[3]
is a key component of many forms of simulation, and fast parallel generation is particularly important for the naturally parallel Monte Carlo simulations that are used extensively in computational finance and many areas of computational science and engineering.
In this chapter we present CUDA implementations of three of the most popular generators that appear in major commercial software libraries: L'Ecuyer's multiple recursive generator MRG32k3a, the Mersenne Twister MT19937, and the Sobol quasi-random generator. Although there is much in common in the underlying mathematical formulation of these three generators, there are also very significant differences, and one of our aims in this chapter is to explain to layman readers why these differences lead to quite different implementations.
In all three cases, there is a
state
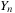 , consisting of one or more variables, which can be advanced, step-by-step, by some algorithm
, consisting of one or more variables, which can be advanced, step-by-step, by some algorithm
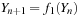 from an initial value
from an initial value
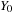 . In addition, there is an output process
. In addition, there is an output process
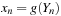 which generates an approximately uniformly distributed random number
which generates an approximately uniformly distributed random number
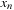 .
.
The parallel implementations are made possible by the fact that each generator can efficiently “skip ahead” a given number of points using a state advance algorithm of the form
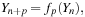 with a cost which is
with a cost which is
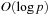 in general. The question then becomes how such a skip ahead should be used. In a broad sense, there are three possible strategies:
in general. The question then becomes how such a skip ahead should be used. In a broad sense, there are three possible strategies:
• Simple skip ahead: each thread in each CUDA thread block performs a skip ahead to a specified point in the generator sequence, and then generates a contiguous segment of points. The skip aheads are chosen so that the segments are adjacent and do not overlap.
• Strided (or “leapfrog”) skip ahead: the
n
-th thread (out of
N
) generates points
n
,
n
+
N
,
n
+ 2
N
, and so on.
• Hybrid: a large skip ahead is performed at the thread block level, and then within a block, each thread does strided generation.
In outline, the approaches used in the three cases are as follows:
• MRG32k3a has a very small state and a very efficient skip ahead, so the simple skip-ahead approach is used. However, care must be taken to achieve memory coalescence in writing the random outputs to device memory.
• The Sobol generator has a very small state and very efficient skip ahead. It could be implemented efficiently using the simple skip-ahead approach, but it is slightly more efficient to use the hybrid approach to achieve simple memory coalescence when writing the output data.
• MT19937 has a very large state and a very slow skip ahead. However, special features of the state advance algorithm make it possible for the threads within a block to work together to advance a shared state. Hence, the hybrid approach is adopted.
The next three sections examine each generator in detail and explain the CUDA implementation. We then present some benchmark figures comparing our implementations against the equivalent parallel generators in the Intel MKL/VSL libraries.
The software described in this chapter is available from The Numerical Algorithms Group (NAG); please see
www.nag.co.uk/numeric/gpus/
or contact
[email protected]
. In addition, the CUDA SDK example “SobolQRNG” has the source code for an implementation of the Sobol generator.
16.2. L'Ecuyer's Multiple Recursive Generator MRG32
k
3
a
16.2.1. Formulation
L'Ecuyer studied combined multiple recursive generators (CMRG) in order to produce a generator that had good randomness properties with a long period, while at the same time being fairly straightforward
to implement. The best known CMRG is MRG32k3a
[4]
, which is defined by the set of equations
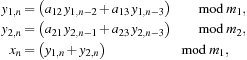 for all
for all
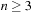 where
where
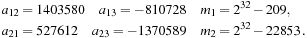 The sequence of integers
The sequence of integers
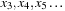 are the output of this generator. When divided by
are the output of this generator. When divided by
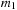 they give pseudorandom outputs with a uniform distribution on the unit interval
they give pseudorandom outputs with a uniform distribution on the unit interval
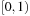 . These may then be transformed into various other distributions.
. These may then be transformed into various other distributions.
(16.1)
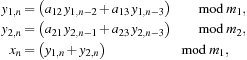
At any point in the sequence the state can be represented by the pair of vectors
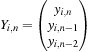 for
for
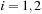 . It follows that the two recurrences in
Eq. 16.1
can be represented as
. It follows that the two recurrences in
Eq. 16.1
can be represented as
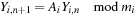 for
for
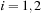 where each
where each
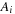 is a
is a
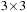 matrix, and therefore
matrix, and therefore
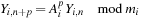 for any
for any
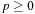 .
.
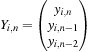
(16.2)
16.2.2. Parallelization
The parallel MRG generator has a small state (only six 32-bit integers) and requires few registers. The simple skip-ahead strategy whereby each thread has its own copy of state and produces a contiguous segment of the MRG32k3a sequence (as specified in
Eq. 16.4
) independently of all other threads works well, provided we have a very efficient way to skip ahead to an arbitrary number of points. To efficiently compute
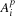 for large values of
p
, one can use the classic “divide-and-conquer” strategy of iteratively squaring the matrix
for large values of
p
, one can use the classic “divide-and-conquer” strategy of iteratively squaring the matrix
 [5]
and
[8]
. It begins by writing
[5]
and
[8]
. It begins by writing
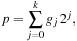 where
where
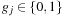 and then computing the sequence
and then computing the sequence
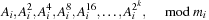 by successively squaring the previous term found. It is then a simple matter to compute
by successively squaring the previous term found. It is then a simple matter to compute
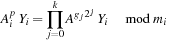 for
for
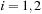 and the entire process can be completed in approximately
and the entire process can be completed in approximately
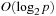 steps.
steps.
We can improve the speed of this procedure at the cost of more memory by expanding the exponent
p
in a base higher than two so that
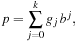 for some
for some
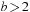 and
and
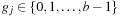 . This improves the “granularity” of the expansion. To illustrate, suppose
b
= 10 and
p
= 7. Then computing
. This improves the “granularity” of the expansion. To illustrate, suppose
b
= 10 and
p
= 7. Then computing
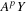 requires only a single lookup from memory; namely, the precomputed value
requires only a single lookup from memory; namely, the precomputed value
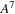 , and a single matrix-vector product. However, if
b
= 2, then
, and a single matrix-vector product. However, if
b
= 2, then
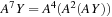 , requiring three lookups and three matrix-vector products.
, requiring three lookups and three matrix-vector products.
16.2.3. Implementation
We take
b
= 8 and precompute the set of matrices
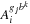 for
for
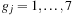 and
and
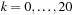 ; namely,
; namely,
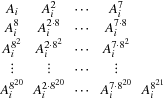 for
for
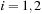 on the host. Because the state is so small, only 10,656 bytes of memory are used, and both sets of matrix powers are copied to constant memory on the GPU. Selecting from this large store of pre-computed matrix powers allows us to compute
on the host. Because the state is so small, only 10,656 bytes of memory are used, and both sets of matrix powers are copied to constant memory on the GPU. Selecting from this large store of pre-computed matrix powers allows us to compute
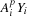 , roughly three times faster than using
b
= 2.
, roughly three times faster than using
b
= 2.
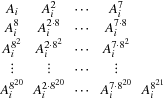
To generate a total of
N
random numbers, a kernel can be launched with any configuration of threads and blocks. Using
T
threads in total, the
i
-th thread for
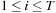 will advance its state by
will advance its state by
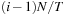 and will then generate
N
/
T
numbers.
and will then generate
N
/
T
numbers.
The most efficient way to use the numbers generated in this manner is to consume them as they are produced, without writing them to global memory. Because any configuration of threads and blocks can be used, and because the MRG generator is so light on resources, it can be embedded directly in an application's kernel. If this is not desired, output can be stored in global memory for subsequent use. Note that each thread generates a contiguous segment of random numbers, and therefore, writes to global memory will
not
be coalesced if they are stored to correspond to the sequence produced by the serial algorithm described in
[4]
; in other words, if the
j
-th value (counting from zero) produced by a given thread is stored at
where
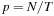 and blocks and grids are one dimensional. Coalesced access can be regained either by reordering output through shared memory, or by simply writing the
j
-th number from each thread to
and blocks and grids are one dimensional. Coalesced access can be regained either by reordering output through shared memory, or by simply writing the
j
-th number from each thread to
storage[j+p*threadIdx.x+p*blockIdx.x*blockDim.x]
storage[threadIdx.x+j*blockDim.x+p*blockIdx.x*blockDim.x]
.
This will result in a sequence in global memory that has a different ordering to the MRG32k3a sequence described in
[4]
.
16.3. Sobol Generator
Sobol
[12]
proposed his sequence as an alternative method of performing numerical integration in a unit hypercube. The idea is to construct a sequence that fills the cube in a regular manner. The integral is then approximated by a simple average of the function values at these points. This approach is very successful in higher dimensions where classical quadrature techniques are very expensive.
Sobol's method for constructing his sequence was improved by Antonov and Saleev
[1]
. Using Gray code, they showed that if the order of the points in the sequence is permuted, a recurrence relation can be found whereby the
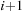 -th point can be generated directly from the
i
-th point in a simple manner. Using this technique, Bratley and Fox
[2]
give an efficient C algorithm for generating Sobol sequences, and this algorithm was used as the starting point for our GPU implementation.
-th point can be generated directly from the
i
-th point in a simple manner. Using this technique, Bratley and Fox
[2]
give an efficient C algorithm for generating Sobol sequences, and this algorithm was used as the starting point for our GPU implementation.
16.3.1. Formulation
We will briefly discuss how to generate Sobol sequences in the unit cube. For more details and further discussion we refer to
[2]
. A
D
-dimensional Sobol sequence is composed of
D
different one-dimensional Sobol sequences. We therefore examine a one-dimensional sequence.
When one is generating at most
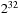 points, a Sobol sequence is defined by a set of 32-bit integers
points, a Sobol sequence is defined by a set of 32-bit integers
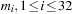 known as
direction numbers
. Using these direction numbers, one can compute the sequence
known as
direction numbers
. Using these direction numbers, one can compute the sequence
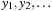 from
from
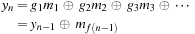 starting from
starting from
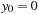 . Here
. Here
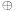 denotes the binary exclusive-or operator, and the
denotes the binary exclusive-or operator, and the
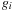 's are the bits in the binary expansion of the Gray code representation of
n
. The Gray code of
n
is given by
's are the bits in the binary expansion of the Gray code representation of
n
. The Gray code of
n
is given by
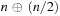 , and so
, and so
 . The function
. The function
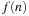 in
Eq. 16.3
returns the index of the rightmost zero bit in the binary expansion of
n
. Finally, to obtain our Sobol sequence
in
Eq. 16.3
returns the index of the rightmost zero bit in the binary expansion of
n
. Finally, to obtain our Sobol sequence
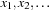 we set
we set
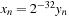 .
.
(16.3)
To obtain multidimensional Sobol sequences, different direction numbers are used for each dimension. Care must be taken in choosing these because poor choices can easily destroy the multidimensional uniformity properties of the sequence. For more details we refer to
[10]
.
16.3.2. Parallelization
The first expression in
Eq. 16.3
gives a formula for directly computing
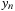 , whereas the second expression gives an efficient algorithm for computing
, whereas the second expression gives an efficient algorithm for computing
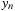 from the value of
from the value of
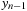 . The first formula therefore allows us to skip ahead to the point
. The first formula therefore allows us to skip ahead to the point
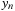 . This skip ahead is quite fast as it requires a loop with at most
32 iterations, and each iteration performs a bit shift and (possibly) an xor. We could therefore have parallelized this generator along the same lines as the MRG32k3a generator described earlier in this chapter with threads performing a skip ahead and then generating a block of points. However, there is another option.
. This skip ahead is quite fast as it requires a loop with at most
32 iterations, and each iteration performs a bit shift and (possibly) an xor. We could therefore have parallelized this generator along the same lines as the MRG32k3a generator described earlier in this chapter with threads performing a skip ahead and then generating a block of points. However, there is another option.
Recall the second expression in
Eq. 16.3
, fix
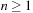 and consider what happens as
n
increases to
n
+ 8. If
and consider what happens as
n
increases to
n
+ 8. If
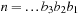 denotes the bit pattern of
n
, clearly the last three bits
denotes the bit pattern of
n
, clearly the last three bits
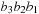 remain unchanged when we add 8 to
n
: adding 1 to
n
eight times results in flipping
remain unchanged when we add 8 to
n
: adding 1 to
n
eight times results in flipping
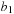 eight times, flipping
eight times, flipping
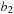 four times and flipping
four times and flipping
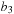 twice. It follows that
twice. It follows that
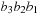 will enumerate all permutations of 3 bits as
n
increases to
n
+ 8. Consider now what happens to
will enumerate all permutations of 3 bits as
n
increases to
n
+ 8. Consider now what happens to
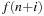 for
for
 : because we are enumerating all permutations of
: because we are enumerating all permutations of
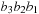 we will have
we will have
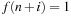 four times,
four times,
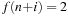 twice,
twice,
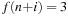 once, and
once, and
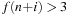 once. Returning to
Eq. 16.3
and recalling that two exclusive-ors cancel (i.e.,
once. Returning to
Eq. 16.3
and recalling that two exclusive-ors cancel (i.e.,
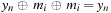 ), we see that
), we see that
 for some
for some
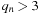 . This analysis can be repeated for any power of 2: in general,
. This analysis can be repeated for any power of 2: in general,
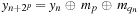 for some
for some
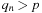 given by
given by
 where | denotes the bitwise or operator. This gives an extremely efficient algorithm for strided (or “leapfrog”) generation, which in turn is good for memory coalescing (see the next section).
where | denotes the bitwise or operator. This gives an extremely efficient algorithm for strided (or “leapfrog”) generation, which in turn is good for memory coalescing (see the next section).
(16.4)
16.3.3. Implementation
Our algorithm works as follows. The
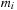 values are precomputed on the host and copied to the device. In a 32-bit Sobol sequence, each dimension requires at most 32 of the
values are precomputed on the host and copied to the device. In a 32-bit Sobol sequence, each dimension requires at most 32 of the
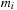 values. Since individual dimensions of the
D
dimensional Sobol sequence are independent, it makes sense to use one block to compute the points of each dimension (more than one block can be used, but suppose for now there is only one). For each Sobol dimension then, a block is launched with
values. Since individual dimensions of the
D
dimensional Sobol sequence are independent, it makes sense to use one block to compute the points of each dimension (more than one block can be used, but suppose for now there is only one). For each Sobol dimension then, a block is launched with
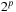 threads for some
threads for some
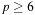 and the 32
and the 32
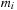 values for that dimension are copied to shared memory. Within the block, the
i
-th thread skips ahead to the value
values for that dimension are copied to shared memory. Within the block, the
i
-th thread skips ahead to the value
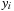 using the first expression in
Eq. 16.3
. Because
p
is typically small (around 6 or 7), the skip-ahead loop will have few iterations (around 6 or 7) because the bit pattern of
using the first expression in
Eq. 16.3
. Because
p
is typically small (around 6 or 7), the skip-ahead loop will have few iterations (around 6 or 7) because the bit pattern of
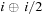 will contain mostly zeros. The thread then iteratively generates points
will contain mostly zeros. The thread then iteratively generates points
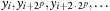 using
Eq. 16.4
. Note that
using
Eq. 16.4
. Note that
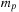 is fixed throughout this iteration: all that is needed at each step is the previous
y
value and the new value of
is fixed throughout this iteration: all that is needed at each step is the previous
y
value and the new value of
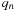 . Writes to global memory are easily coalesced because successive threads in a warp generate successive values in the Sobol sequence. In global memory we store all the numbers for the first Sobol dimension first, then all the numbers for the second Sobol dimension, and so on. Therefore, if
N
points were generated from a
D
dimensional Sobol sequence and stored in an array
x
, the
i
-th value of the
d
-th dimension would be located at
x[d*N+i]
where
. Writes to global memory are easily coalesced because successive threads in a warp generate successive values in the Sobol sequence. In global memory we store all the numbers for the first Sobol dimension first, then all the numbers for the second Sobol dimension, and so on. Therefore, if
N
points were generated from a
D
dimensional Sobol sequence and stored in an array
x
, the
i
-th value of the
d
-th dimension would be located at
x[d*N+i]
where
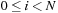 and
and
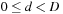 .
.
As a final tuning of the algorithm, additional blocks can be launched for each dimension as long as the number of blocks cooperating on a given dimension is a power of 2. In this case if
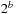 blocks cooperate, the
i
-th thread in a block simply generates the points
blocks cooperate, the
i
-th thread in a block simply generates the points
 .
.
The Mersenne Twister (MT19937) is a pseudorandom number generator proposed by Matsumoto and Nishumira
[11]
. It is a twisted generalized feedback shift register (TGFSR) generator featuring state bit reflection and tempering. The generator has a very long period of
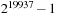 and good multidimensional uniformity and statistical properties. The generator is also relatively fast compared with similar quality algorithms, and therefore, it is widely used in simulations where huge quantities of high-quality random numbers are required.
and good multidimensional uniformity and statistical properties. The generator is also relatively fast compared with similar quality algorithms, and therefore, it is widely used in simulations where huge quantities of high-quality random numbers are required.
We start by discussing the rather complex-looking mathematical formulation. We then present the relatively simple sequential implementation, which some readers may prefer to take as the specification of the algorithm, before proceeding to the parallel implementation.
16.4.1. Formulation
TGFSR generator is based on the linear recurrence
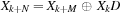 for all
for all
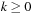 where
where
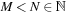 are given and fixed. Each value
are given and fixed. Each value
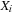 has a word length of
w
that is represented by
w
0–1 bits. The value
D
is a
has a word length of
w
that is represented by
w
0–1 bits. The value
D
is a
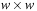 matrix with 0–1 entries, the matrix multiplication in the last term is performed modulo 2, and
matrix with 0–1 entries, the matrix multiplication in the last term is performed modulo 2, and
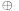 is again bitwise exclusive-or, which corresponds to bitwise addition modulo 2. These types of generators have several advantages: they are easy to initialize (note that we need
N
seed values), they have very long periods, and they have good statistical properties.
is again bitwise exclusive-or, which corresponds to bitwise addition modulo 2. These types of generators have several advantages: they are easy to initialize (note that we need
N
seed values), they have very long periods, and they have good statistical properties.
The Mersenne Twister defines a family of TGFSR generators with a separate output function for converting state elements into random numbers. The output function applies a
tempering transform
to each generated value
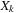 before returning it (see
[11]
for further details) where the transform is chosen to improve the statistical properties of the generator. The family of generators is based on the recurrence
before returning it (see
[11]
for further details) where the transform is chosen to improve the statistical properties of the generator. The family of generators is based on the recurrence
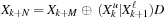 for all
for all
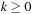 where
where
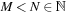 are fixed values and each
are fixed values and each
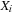 has a word length of
w
. The expression
has a word length of
w
. The expression
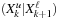 denotes the concatenation of the
denotes the concatenation of the
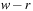 most significant bits of
most significant bits of
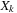 and the
r
least significant bits of
and the
r
least significant bits of
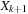 for some
for some
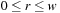 , and the
, and the
 bit-matrix
D
is given by
bit-matrix
D
is given by
 where all the entries
where all the entries
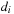 are either zero or one. The matrix multiplication in
Eq. 16.5
is performed bitwise modulo 2.
are either zero or one. The matrix multiplication in
Eq. 16.5
is performed bitwise modulo 2.
(16.5)

The popular Mersenne Twister MT19937
[11]
is based on this scheme with
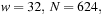
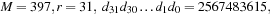 and has a period equal to the Mersenne prime
and has a period equal to the Mersenne prime
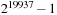 . The state vector of MT19937 consists of
. The state vector of MT19937 consists of
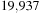 bits
— 623 unsigned 32-bit words plus one bit — and is stored as 624 32-bit words. We denote this state vector by
bits
— 623 unsigned 32-bit words plus one bit — and is stored as 624 32-bit words. We denote this state vector by
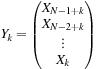 for all
for all
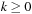 where
where
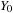 denotes the initial seed. When read from top to bottom, the first 19,937 bits are used and the bottom 31 bits (the 31 least significant bits of
denotes the initial seed. When read from top to bottom, the first 19,937 bits are used and the bottom 31 bits (the 31 least significant bits of
 ) are ignored. If the generator is considered as an operation on individual
bits
, it can be recast in the form
) are ignored. If the generator is considered as an operation on individual
bits
, it can be recast in the form
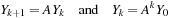 where
A
is a matrix of dimension 19,937 with elements having value 0 or 1 and the multiplication is performed mod 2. For the explicit form of this matrix, see
[11]
.
where
A
is a matrix of dimension 19,937 with elements having value 0 or 1 and the multiplication is performed mod 2. For the explicit form of this matrix, see
[11]
.
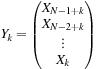
(16.6)
Matsumoto and Nishimura give a simple C implementation of their algorithm that is shown in
Listing 16.1
. Their implementation updates all 624 elements of state at once so that the
state
variable contains
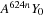 for
for
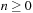 . The subsequent 624 function calls each produce a single random number without updating any state, and the 625-th call will again update the state.
. The subsequent 624 function calls each produce a single random number without updating any state, and the 625-th call will again update the state.
 |
| Listing 16.1
Serial implementation of MT19937.
|
16.4.2. Parallelization
The state size of the Mersenne Twister is too big for each thread to have its own copy. Therefore, the per-thread parallelization strategy used for the MRG32k3a is ruled out, as is the strided generation strategy used for the Sobol generator. Instead, threads within a block have to cooperate to update state and generate numbers, and the level to which this can be achieved determines the performance of the generator. Note from
Eq. 16.5
that the process of advancing state is quite cheap, involving three state elements and 7 bit operations.
We follow a hybrid strategy. Each block will skip the state ahead to a given offset, and the threads will then generate a contiguous segment of points from the MT19937 sequence by striding (or leapfrogging). There are three main procedures: skipping ahead to a given point, advancing the state, and generating points from the state. We will examine how to parallelize the latter two procedures first, and then return to the question of skipping ahead.
16.4.3. Updating State and Generating Points
Generating
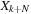 for any
for any
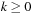 requires the values of
requires the values of
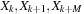 where
where
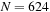 and
and
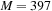 . In particular,
. In particular,
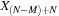 requires
requires
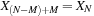 . If there are
T
threads in a block and the
i
-th thread generates
. If there are
T
threads in a block and the
i
-th thread generates
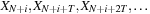 for
for
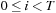 , then we see that we must have
, then we see that we must have
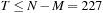 ; otherwise, thread
; otherwise, thread
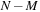 would require
would require
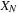 , a value that will be generated by thread 0. To avoid dependence between threads, we are limited to fewer than 227 threads per block. We will use 1-D blocks with 224 threads because this is a multiple of 32.
, a value that will be generated by thread 0. To avoid dependence between threads, we are limited to fewer than 227 threads per block. We will use 1-D blocks with 224 threads because this is a multiple of 32.
We implement state as a circular buffer in shared memory of length
 , and we update 224 elements at a time. We begin by generating 224 random numbers from the initial seed and then updating 224 elements of state and storing them at locations
state[N…N+223]
. This process repeats as often as needed, with the writing indices wrapping around the buffer. All indices except writes to global memory are computed modulo
, and we update 224 elements at a time. We begin by generating 224 random numbers from the initial seed and then updating 224 elements of state and storing them at locations
state[N…N+223]
. This process repeats as often as needed, with the writing indices wrapping around the buffer. All indices except writes to global memory are computed modulo
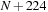 . The code is illustrated in
Listing 16.2
. As was the case with the Sobol generator, writes to global memory are easily coalesced because the threads cooperate in a leapfrog manner.
. The code is illustrated in
Listing 16.2
. As was the case with the Sobol generator, writes to global memory are easily coalesced because the threads cooperate in a leapfrog manner.
 |
| Listing 16.2
CUDA code for generating points and updating state for MT19937. The code follows the general notation of
Listing 16.1
.
|
We now consider how blocks can skip ahead to the correct point in the sequence. Given a certain number of Mersenne points to generate, we wish to determine how many points each block should produce and then skip that block ahead by the number of points all the preceding blocks will generate. For this we need a method to skip a single block ahead by a given number of points in the Mersenne sequence.
Such a skip-ahead algorithm was presented by Haramoto
et al.
[9]
. Recall that
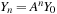 for
for
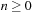 where
A
is a 19,937 × 19,937 matrix. However computing
where
A
is a 19,937 × 19,937 matrix. However computing
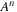 even through a repeated squaring (or “divide-and-conquer”) strategy is prohibitively expensive and would require a lot of memory. Instead,
a different approach is followed in
[9]
based on polynomials in the field
even through a repeated squaring (or “divide-and-conquer”) strategy is prohibitively expensive and would require a lot of memory. Instead,
a different approach is followed in
[9]
based on polynomials in the field
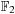 (the field with elements
(the field with elements
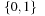 and where all operations are performed modulo 2). Briefly, they show that for any
and where all operations are performed modulo 2). Briefly, they show that for any
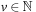 we have
we have
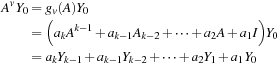 where
where
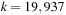 and
and
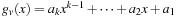 is a polynomial over
is a polynomial over
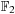 that depends on
v
. A formula is given for determining
that depends on
v
. A formula is given for determining
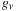 for any
for any
 given and fixed. Note that each of the coefficients
given and fixed. Note that each of the coefficients
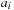 of
of
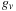 are either zero or one.
are either zero or one.
(16.7)
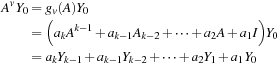
Figure 16.1
shows the time taken for a single block to perform the various tasks in the MT19937 algorithm: calculate
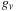 on the host, compute
on the host, compute
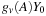 , perform
v
updates of state (not generating points from state), and generating
v
values with all updates of state. Although evaluating
, perform
v
updates of state (not generating points from state), and generating
v
values with all updates of state. Although evaluating
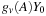 is
fairly expensive (equivalent to generating about 2million points and advancing state about 2.3million times), computing the polynomial
is
fairly expensive (equivalent to generating about 2million points and advancing state about 2.3million times), computing the polynomial
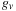 is is much more so: one could generate almost 13million points in the same time, and advance state almost 20million times. Updating state and generating points scale linearly with
v
.
is is much more so: one could generate almost 13million points in the same time, and advance state almost 20million times. Updating state and generating points scale linearly with
v
.
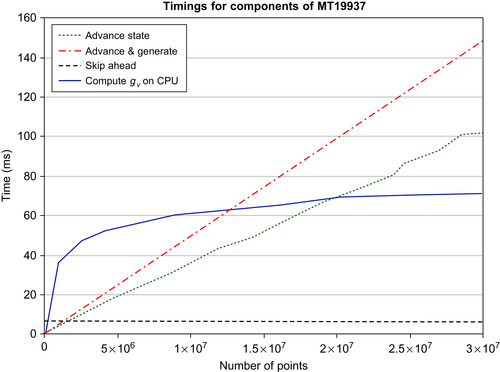 |
| Figure 16.1
Time (in ms) for one block of 224 threads to (a) advance state
v
times (without generating points); (b) advance state
v
times and generate points; (c) apply the skip-ahead algorithm in
Eq. 16.7
; and (d) compute the skip-ahead polynomial
|
Clearly, we would prefer not to calculate
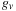 on the fly. We would also prefer not to perform the calculation
on the fly. We would also prefer not to perform the calculation
 in a separate kernel because the first block never has to skip ahead and this would prevent it from generating points until the calculation was finished. However, there is the question of load balance: the first block can generate around 2million points in the time it takes the second block to skip ahead. Because the total runtime is equal to the runtime of the slowest block, if the number of blocks equals the number of streaming multiprocessors in the GPU, it is clear that blocks should not all generate the same number of points. A mathematical analysis of the runtimes of each block, coupled with experimental measurements, can be done, and this yields formulae for the optimal number of points each block should generate as well as how far the block should skip ahead. This depends on the sample size and so requires us to calculate
in a separate kernel because the first block never has to skip ahead and this would prevent it from generating points until the calculation was finished. However, there is the question of load balance: the first block can generate around 2million points in the time it takes the second block to skip ahead. Because the total runtime is equal to the runtime of the slowest block, if the number of blocks equals the number of streaming multiprocessors in the GPU, it is clear that blocks should not all generate the same number of points. A mathematical analysis of the runtimes of each block, coupled with experimental measurements, can be done, and this yields formulae for the optimal number of points each block should generate as well as how far the block should skip ahead. This depends on the sample size and so requires us to calculate
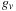 on the fly.
on the fly.
There are a number of options when choosing a skip-ahead strategy for the Mersenne Twister, and it is not completely clear which approach is best:
• When a huge number of points are to be generated, the only option may be to generate the necessary polynomials on the fly and perform
Eq. 16.7
on the device. In this case the generator will typically be embedded in a larger application so that the cost of computing the polynomials is small compared with the total runtime.
• When a small number of points are to be generated it may be more efficient to have a producer-consumer model where one (or a few) blocks advance state and write the values to global memory, while other blocks read these values in and generate points from the necessary distributions. This requires rather sophisticated interblock communication using global memory locks and relies on the update of state shown in
Eq. 16.5
being much cheaper than converting state into a given distribution. It is not clear how useful this would be, and indeed for smaller samples, it will probably be faster (and simpler) to compute the numbers on the host.
• When a medium number of points are to be generated, it is possible to precompute and store a selection of polynomials
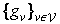 for some
for some
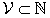 . At runtime a suitable subset of these can be chosen and copied to the device where the skip ahead is then performed. This is the approach we have adopted. The difficulty here is deciding on
. At runtime a suitable subset of these can be chosen and copied to the device where the skip ahead is then performed. This is the approach we have adopted. The difficulty here is deciding on
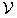 and on which subset to choose at runtime. Formulae can be developed to help with this, but it is still a rather tricky problem.
and on which subset to choose at runtime. Formulae can be developed to help with this, but it is still a rather tricky problem.
• Lastly, we can always calculate
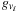 and
and
 for all necessary skip points
for all necessary skip points
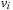 on the host and then copy the advanced states to the device to generate random numbers. This is currently impractical, but the upcoming Westmere family of Intel CPUs contains a new instruction
PCLMULQDQ
— a bitwise carry-less multiply — that is ideally suited to this task; see
[7]
for further details.
on the host and then copy the advanced states to the device to generate random numbers. This is currently impractical, but the upcoming Westmere family of Intel CPUs contains a new instruction
PCLMULQDQ
— a bitwise carry-less multiply — that is ideally suited to this task; see
[7]
for further details.
16.5. Performance Benchmarks
We compared our CUDA implementations with the Intel MKL/VSL library's random number generators. Benchmarks were done in both single and double precision on a Tesla C1060 and a Tesla
C2050 (that uses the new Fermi micro architecture). The test system configuration is detailed in
Table 16.1
.
The Intel random number generators are contained in the vector statistical library (VSL). This library is not multithreaded, but is thread safe and contains all the necessary skip-ahead functions to advance the generators’ states. We used OpenMP to parallelize the VSL generators and obtained figures when running one, two, three and four CPU threads. Timing of the CPU code was done using hardware high-resolution performance counters; the GPU code was timed using CUDA events and
cudaEvent ElapsedTime
. Ideally, an application would consume the random numbers on the GPU, however, if the random numbers were required by CPU code, then there may be an additional cost to copy the data back from the GPU to the host. A fixed problem size of
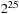 was chosen so that each generator produced 33,554,432 floating-point numbers. This corresponds to 134MB of data in single precision and 268MB in double precision. For the Sobol generators we chose
was chosen so that each generator produced 33,554,432 floating-point numbers. This corresponds to 134MB of data in single precision and 268MB in double precision. For the Sobol generators we chose
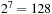 dimensions and generated
dimensions and generated
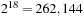 multidimensional points. Note that the VSL does not have skip-ahead functions for the MT19937 generator, so it was not possible to parallelize this generator.
multidimensional points. Note that the VSL does not have skip-ahead functions for the MT19937 generator, so it was not possible to parallelize this generator.
We produced uniform exponential and normal random numbers. For the MRG the normal random numbers were obtained through a Box-Muller transform whereas for the Sobol and Mersenne generators the normal random numbers were obtained by inverting the cumulative normal distribution function using an efficient implementation of the inverse error function
[6]
. Exponential numbers were obtained by inverting the cumulative exponential distribution function. The results are given in
Table 16.2
and
Table 16.3
.
| Generators | Tesla GPU | Intel MKL on Xeon E5410 | ||||
|---|---|---|---|---|---|---|
| GPU pts/ms | 1 Thread | 2 Threads | 3 Threads | 4 Threads | ||
| MRG | Unif | 3.6151E+06 | 41.161x | 24.774x | 19.639x | 16.247x |
| 3.1202E+06 | 45.528x | 31.094x | 30.887x | 29.889x | ||
| Exp | 2.8280E+06 | 39.545x | 23.222x | 17.882x | 14.964x | |
| 6.8651E+05 | 12.329x | 7.634x | 6.724x | 6.468x | ||
| Norm | 2.6647E+06 | 47.043x | 25.619x | 18.498x | 15.188x | |
| 6.5853E+05 | 18.012x | 10.257x | 7.463x | 6.215x | ||
| Sobol | Unif | 1.5790E+07 | 100.51x | 93.976x | 94.179x | 64.556x |
| 9.2006E+06 | 7.591x | 90.396x | 84.130x | 88.832x | ||
| Exp | 6.8723E+06 | 52.591x | 41.702x | 33.784x | 32.251x | |
| 7.8709E+05 | 10.622x | 8.683x | 7.398x | 7.432x | ||
| Norm | 7.4239E+06 | 57.079x | 45.129x | 35.896x | 34.820x | |
| 4.0799E+05 | 5.516x | 4.578x | 3.915x | 3.856x | ||
| Mersenne | Unif | 2.6721E+06 | 25.051x | |||
| 2.5762E+06 | 40.320x | |||||
| Exp | 2.0741E+06 | 24.758x | ||||
| 5.9492E+05 | 19.728x | |||||
| Norm | 2.0657E+06 | 24.856x | ||||
| 3.1229E+05 | 5.8127x | |||||
| Generators | Fermi GPU | Intel MKL on Xeon E5410 | ||||
|---|---|---|---|---|---|---|
| GPU pts/ms | 1 Thread | 2 Threads | 3 Threads | 4 Threads | ||
| MRG | Unif | 7.7127E+06 | 88.108x | 52.854x | 41.900x | 34.622x |
| 7.4453E+06 | 108.64x | 74.197x | 73.703x | 71.321x | ||
| Exp | 5.4368E+06 | 76.024x | 44.643x | 34.378x | 28.767x | |
| 2.6696E+06 | 47.935x | 29.682x | 26.143x | 25.148x | ||
| Norm | 4.6129E+06 | 81.436x | 44.348x | 32.022x | 26.291x | |
| 2.4418E+06 | 66.789x | 38.034x | 27.673x | 23.044x | ||
| Sobol | Unif | 1.7434E+07 | 110.97x | 103.76x | 103.98x | 71.724x |
| 1.3452E+07 | 142.68x | 132.16x | 123.00x | 129.88x | ||
| Exp | 7.9361E+06 | 60.732x | 48.157x | 39.014x | 37.243x | |
| 3.2094E+06 | 43.312x | 35.404x | 30.168x | 30.304x | ||
| Norm | 8.6020E+06 | 66.137x | 52.291x | 41.593x | 40.346x | |
| 1.6202E+06 | 21.904x | 18.179x | 15.547x | 15.314x | ||
| Mersenne | Unif | 2.9077E + 06 | 27.260x | |||
| 2.8728E+06 | 44.961x | |||||
| Exp | 2.2352E+06 | 26.680x | ||||
| 1.2465E+06 | 23.097x | |||||
| Norm | 2.1965E+06 | 26.430x | ||||
| 8.8145E+05 | 16.407x | |||||
All benchmarks were performed after a clean reboot of the workstation, with only a command prompt open. There does seem to be some variability in the figures across different runs, depending on system load, but this is small enough to be ignored. For the Mersenne Twister we precomputed
the skip-ahead polynomials
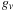 for
for
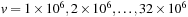 and then used a combination of redundant state advance (without generating points) and runtime equations to find a good workload for each thread block.
and then used a combination of redundant state advance (without generating points) and runtime equations to find a good workload for each thread block.
The Fermi card is roughly twice as fast as the Tesla in single precision, and roughly four times as fast in double precision. The exception to this is the Sobol single precision figures, which are very similar between the two cards. It may be that the Sobol generator is bandwidth limited because Sobol values (in single precision) are so cheap to compute.
Acknowledgments
Jacques du Toit thanks the UK Technology Strategy Board for funding his KTP Associate position with the Smith Institute, and Mike Giles thanks the Oxford-Man Institute of Quantitative Finance for its support.
[1]
I.A. Antonov, V.M. Saleev,
An economic method of computing
LP
τ
sequences
,
USSR J. Comput. Math. Math. Phys.
19
(1979
)
252
–
256
.
[2]
P. Bratley, B. Fox,
Algorithm 659: implementing Sobol's quasirandom sequence generator
,
ACM Trans. Model. Comput. Simul.
14
(1
) (1988
)
88
–
100
.
[3]
P. L'Ecuyer,
Uniform random number generation
,
In: (Editors: S.G. Henderson, B.L. Nelson)
Simulation Handbooks in Operation Research and Management Science
(2006
)
Elsevier Inc.
,
Amsterdam
, pp.
55
–
81
.
[4]
P. L'Ecuyer,
Good parameter sets for combined multiple recursive random number generators
,
Ops. Rsch.
47
(1
) (1999
)
159
–
164
.
[5]
P. L'Ecuyer, R. Simar, E.J. Chen, W.D. Kelton,
An object oriented random number package with many long streams and substreams
,
Ops. Rsch.
50
(6
) (2002
)
1073
–
1075
.
[6]
M. Giles, Approximating the
erfinv
function, in: GPU Gems 4, vol. 2.
[7]
S. Gueron, M.E. Kounavis, Intel carry-less multiplication instruction and its usage for computing the GCM mode, Intel White Paper,
http://software.intel.com/en-us/articles/intel-carry-less-multiplication-instruction-and-its-usage-for-computing-the-gcm-mode/
.
[8]
D. Knuth,
third ed.
The Art of Computer Programming
.
vol. 2
(1997
)
Addison-Wesley Professional
,
Reading, MA
.
[9]
H. Haromoto, M. Matsumoto, T. Nishumira, F. Panneton, P. L'Ecuyer,
Efficient jump ahead for
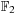 -linear random number generators
,
INFORMS J. Comput.
20
(3
) (2008
)
385
–
390
.
-linear random number generators
,
INFORMS J. Comput.
20
(3
) (2008
)
385
–
390
.
[10]
S. Joe, F.Y. Kuo,
Constructing Sobol sequences with better two dimensional projects
,
SIAM J. Sci. Comput.
30
(2008
)
2635
–
2654
.
[11]
M. Matsumoto, T. Nishumira,
Mersenne Twister: a 623-dimensionally equidistributed uniform pseudo-random number generator
,
ACM Trans. Mod. Comput. Simul.
8
(1
) (1998
)
3
–
30
.
[12]
I.M. Sobol,
On the distribution of points in a cube and the approximate evaluation of integrals
,
USSR Comput. Math. Math. Phys.
16
(1967
)
1332
–
1337
.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
