Micro- and nanorobots in Newtonian and biological viscoelastic fluids
Stefano Palagi⁎; Debora Walker⁎; Tian Qiu⁎,†; Peer Fischer⁎,‡ ⁎Max Planck Institute for Intelligent Systems, Stuttgart, Germany
†Swiss Federal Institute of Technology in Lausanne, Lausanne, Switzerland
‡University of Stuttgart, Stuttgart, Germany
Abstract
Swimming microorganisms are a source of inspiration for small scale robots that are intended to operate in fluidic environments including complex biomedical fluids. Nature has devised swimming strategies that are effective at small scales and at low Reynolds number. These include the rotary corkscrew motion that, for instance, propels a flagellated bacterial cell, as well as the asymmetric beat of appendages that sperm cells or ciliated protozoa use to move through fluids. These mechanisms can overcome the reciprocity that governs the hydrodynamics at small scale. The complex molecular structure of biologically important fluids presents an additional challenge for the effective propulsion of microrobots. In this chapter it is shown how physical and chemical approaches are essential in realizing engineered abiotic micro- and nanorobots that can move in biomedically important environments. Interestingly, we also describe a microswimmer that is effective in biological viscoelastic fluids that does not have a natural analogue.
Keywords
Microrobot; Nanorobot; Microswimmer; Non-Newtonian; Viscoelastic fluid; Biological fluid; Biomedical robotics
8.1 Introduction
Many microorganisms and cells can move in liquid media by a variety of strategies that involve periodic body-shape changes, e.g. by moving one or more appendages. These biological micro-scale swimmers (or microswimmers) can self-propel in a variety of different media, including both Newtonian and non-Newtonian fluids (see Box 1). Such features are also appealing for untethered micro- and nano-scale robots, especially for those intended for medical applications, since they will be required to actively move in the complex environment found in the human body. Therefore, biological microswimmers have become a great source of inspiration in the design of micro- and nanorobots that have to move in fluids.
Newtonian fluids as simple as water already present their own considerable challenges for micro-scale swimmers. At such a small scale, the characteristic Reynolds number Re, which represents the ratio between inertial and viscous forces, is lower than unity, thus inertia is negligible and time-reversibility applies (low-Re regime). This means that reciprocal motions, such as the opening and closing of a single-hinge mechanism, lead to no net displacement, no matter how fast or slow the different phases are (which is known as the scallop theorem [2]). In other words, small scale organisms and devices must perform complex non-reciprocal motions to effectively swim in Newtonian fluids. The main strategies adopted by microorganisms and cells to swim in such conditions rely on three different kinds of propellers and appendages:
■ the bacterial flagellum, a rotating helical propeller, whose chiral shape leads to symmetry-breaking and non-reciprocity;
■ the eukaryotic flagellum, a flexible appendage whose beat in solution generates a traveling-wave-like non-reciprocal motion;
■ cilia, short appendages that beat in an asymmetric and self-coordinated fashion.
In Section 8.2, the mechanism of propulsion based on cilia is further described, along with the development of a soft microrobot that swims in a Newtonian fluid by a mechanism inspired by ciliary propulsion found in unicellular protozoa – microorganisms called ciliates.
Microrobots moving in Newtonian fluids similar to bacterial flagella are considered in Section 8.3. The microrobots consist of a rigid helical micro-structure that is rotated in the fluid by a torque applied by an external magnetic field. In Section 8.3 we show that the same propulsion principle can be applied to achieve movement in non-Newtonian media. To do so, two distinct strategies are adopted. One relies on down-scaling the robots from the micro- to the nano-scale, which allows them to effectively move through a gel-like biological medium constituted by a hyaluronan polymeric network. The other strategy mimics the behavior of the bacterium, Helicobacter pylori, which moves through mucus by changing its viscosity chemically.
In Section 8.4 we present an artificial microrobot that has no biological analogue and that swims in non-Newtonian fluids by a simple reciprocal motion. This microrobot actually exploits the rheological properties of biomedically important fluids and achieves propulsion even with a single-hinge opening and closing mechanism, thus circumventing Purcell's scallop theorem.
8.2 Self-propelled soft microswimmers and microrobots
Most artificial microrobots that have been reported so far embed no actuators, and often consist of rigid monolithic structures made of hard materials. Alternatively, if they consist of flexible materials, they at best contain only a small number of passive degrees of freedom that are actuated by external fields. The external field (e.g. a magnetic field) directly exerts forces and torques on the microrobot's body that result in its motion (propulsion).
A variety of biological propulsion mechanisms at different scales are based on the common principle of traveling waves. These basically consist of periodic deformations that travel along one or more appendages, or along the whole body of the organism. An artificial microrobot must therefore be constituted of soft or flexible materials to perform such body-shape changes. Moreover, since in nature these emerge from the internal action of distributed molecular motors, a truly bioinspired microrobot should also be capable of generating the required driving forces internally. This means that, in addition to being soft, the microrobot must possess internal actuation.
8.2.1 Inspiration: Ciliary propulsion and metachronal waves
Eukaryotic flagella and cilia are thin appendages (about 200 nm in diameter) that have identical internal structure, but different lengths: whereas flagella can be as long as several centimeters, cilia are usually much shorter (about 10 μm long) [1]. Although these organelles are apparently identical, the term flagellum is used when there is only one or a small number of these appendages on a cell (e.g. spermatozoa and flagellates), whereas the term cilia is used to denote large numbers of them on the same cell [3]. These appendages are substantially different from bacterial flagella. Indeed, the latter are passive propellers actuated by a rotary motor at their base, whereas eukaryotic flagella and cilia are active flexible organelles whose actuation is distributed along their length. They possess a complex internal structure (called axoneme), most commonly consisting of nine microtubule doublets spaced around the circumference and two microtubules in the center (which is also known as the 
configuration), all of them running along the length of the appendage. Dynein molecular motors are distributed between the doublets and slide them back and forth along the length of the appendage, thus generating internal stresses resulting in bending deformations that propagate along the appendage [1].
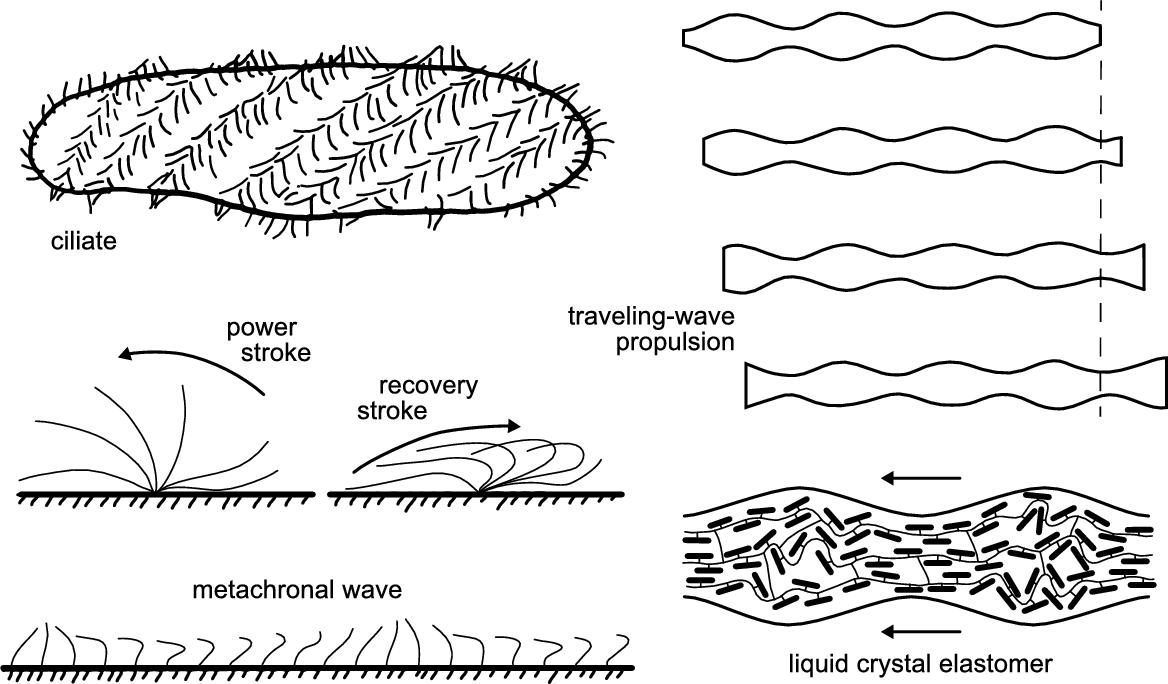
Ciliary propulsion is extremely widespread in nature. Cilia can indeed be found on a variety of eukaryotic cells. These also include a group of unicellular protozoa whose whole surface is covered by cilia, thus these microorganisms are called ciliates (see Fig. 8.1). The coordinated beating of thousands of cilia is responsible for propelling the body of the microorganism through the fluid at high swimming speeds. Indeed, large ciliates such as those belonging to the genus Paramecium have typically a size of a few hundred microns and can self-propel at speeds well above one millimeter per second [4].
8.2.1.1 Motion of a single cilium and metachronal coordination
Individual cilia deform in a non-reciprocal fashion, with a typical beat consisting of two phases: a high-friction effective (power) stroke and a low friction recovery stroke (see Fig. 8.1). Cilia may beat in a vertical plane, but in most cases the recovery stroke involves motions sideways to the cell surface. This basic motion seems effective from a fluid mechanical point of view [3]. On top of this, closely packed cilia arrays display collective behavior that results in apparent traveling-wave deformations of the surface of the microorganism, which are termed metachronal waves (see Fig. 8.1). Notably, the internal actuation of each cilium is independent from that of its neighbors, and they only communicate with each other through the fluid. Because of interactions among the cilia, each cilium beats with a small constant phase difference with respect to its neighbors, leading to the emergence of propagating waves of deformation. The origin of this collective behavior has been the subject of several theoretical investigations. It has been demonstrated that two cilia starting with a random phase difference in their motion end up beating in perfect synchrony, whereas waves with cilia beating with small phase shifts arise naturally in large cilia arrays [5]. Moreover, as the coordination among beating cilia develops from an arbitrary initial condition, their rate of work decreases [6], since, because of viscous drag, it is energetically advantageous for a cilium to beat in the presence of neighboring cilia with a similar phase [1].
In nature several forms of metachronal coordination can be found, exhibiting different propagation directions with respect to the cilia's power stroke direction. For instance, the case in which the wave of deformation propagates in the same direction as the effective stroke is referred to as symplectic metachrony. A typical protozoan exhibiting symplectic metachrony is the species Opalina ranarum, a disc-shaped microorganism that inhabits the gut of frogs. The opposite situation, termed antiplectic metachrony, occurs when the wave velocity and the effective stroke are in opposite directions. Additional complexity arises from the possibility that the phase of cilia may also vary in a lateral direction, such that metachronal waves propagate obliquely or even at right angles to the plane of the cilia's beat. The coordination observed in Paramecium, which is sometimes considered to be antiplectic metachrony, can be more accurately defined as dexioplectic metachrony. Notably, in spite of having cilia beating motions similar to Opalina, the Paramecium can actually be ten times faster [3]. This suggests that the most compelling advantage of ciliary propulsion possibly is its flexibility. The distribution and coordination of a large number of essentially identical organelles has evolved for optimal propulsion of a cell body of given shape and size and can also adapt to different environmental conditions [7].
8.2.2 Self-propulsion of soft microrobots by traveling-wave deformations
Although the flexibility and performance of natural ciliary propulsion may seem appealing for the development of swimming microrobots, replicating the complexity of the complete ciliary machinery in artificial devices is currently unfeasible at the microscale. Ciliary propulsion involves, indeed, two levels of symmetry breaking that is achieved by self-coordination of distributed actuators at two different scales, i.e. at the intra-cilium scale (beating motion obtained by distributed molecular motors) and at the inter-cilia scale (metachrony). Directly mimicking this method of propulsion would therefore require the independent actuation of each hypothetical artificial cilium, such that the two-phase asymmetric beating pattern of natural cilia could be achieved, and the implementation of precise coordination among thousands of such artificial cilia within a sub-millimeter-sized robot.
8.2.2.1 Traveling-wave propulsion
A simpler route to ciliary-inspired artificial propulsion consists in mimicking it at the macroscopic level of metachronal waves, rather than in its microscopic details. From the metachronal coordination observed in swimming ciliates, the principle of surface traveling-wave propulsion can be extracted and applied to the design of swimming microrobots (see Fig. 8.1) [8]. The concept of traveling-wave swimming at low Re was theoretically explored by Sir Geoffrey Taylor in the 1950s to explain the self-propulsion of eukaryotic flagellates and spermatozoa, which send “waves of lateral displacement down a thin tail or flagellum” [9]. To understand this behavior, he modeled the self-propulsion in a viscous fluid of a sheet down which waves of lateral deformation are propagated, since then referred to as Taylor's swimming sheet. This theoretical model has further been developed to also explain ciliary propulsion [10]. It is assumed that closely spaced waving cilia will induce a fluid velocity field very much as if the ciliary tips were replaced by a continuous envelope, to which the adjacent fluid adheres. In this so-called envelope model of ciliary propulsion, the detailed beating motion of individual cilia plays no direct role, and the parameters that enter are actually those of the observed metachronal waves. These assumptions greatly simplify the modeling of ciliary propulsion; nonetheless, the envelope model can deal with important aspects like the different kinds of metachrony [3].
A few artificial microswimmers propelled by traveling waves have been proposed. Dreyfus et al. developed a microswimmer consisting of a chain of magnetic microparticles linked by DNA fragments, which allowed for the chain's flexibility [11]. The chain was attached on one side to a red blood cell, which acted as the head of the microswimmer and broke its symmetry. The flexible chain was actuated by the superposition of two external magnetic fields, a homogeneous static one parallel to the filament, and a sinusoidal one applied in the perpendicular direction, resulting in a field oscillating along the rest axis of the filament. The effective magnetic torque on each microparticle in the chain was the result of a superposition of the externally applied oscillating field and of the dipolar interactions with the neighboring beads, resulting in an undulation that propagated from the end of the chain to the attachment point. More recently Diller et al. presented an artificial swimmer of several-millimeters length that physically implements Taylor's swimming sheet [12]. The device consisted of a flexible sheet with a pre-programmed distributed magnetization profile, which enabled propulsive continuous undulatory deformation to be generated by an external magnetic field rotating in the plane perpendicular to the plane of the sheet. The motion of the sheet was controlled in 2D at the water–air interface. Both these artificial devices swim by traveling-wave deformations, but also require actions (i.e. forces and/or torques) to be directly exerted from the outside by means of an external field to generate such body-shape changes. This is due to the fact that the implementation of actuators, which would be required in large numbers for achieving traveling-wave deformations, is practically unfeasible in such small robotic agents. Nonetheless, the obtained deformations are pre-programmed in the material body of the device by defining its magnetic properties during the fabrication stage. The pre-programmed shape changes are in contrast to the extraordinary flexibility and adaptability shown by biological ciliary propulsion.
8.2.2.2 Self-propelled swimming microrobots
Recently, our group presented microrobots that swim by traveling-wave deformations generated by internal actuation, rather than by direct external actions [13]. These artificial self-propelled microswimmers consist of a soft active material, namely a liquid-crystal elastomer (LCE), which undergoes a reversible shape change (up to 30% length contraction) when heated or illuminated. We have exploited the photoresponse of the LCE to power and control intra-body shape changes in the microrobots by structured light, i.e. by the dynamic projection of light patterns. Localized shape changes can be obtained by selectively illuminating specific parts of the microrobots' body. The microrobot is thus regarded as a continuously addressable actuator that acts as an extended array of many smaller actuation units, each of which is independently triggered by the local light field. This also allows the burden of synchronization and coordination to be transferred from the microrobot to the light field, thereby simplifying its design and fabrication. In particular, the projection of periodic binary light patterns leads to periodic, wave-like deformations of the soft microrobots. Therefore, propulsive traveling-wave deformations can be achieved by projecting traveling periodic light patterns. Indeed, a one-millimeter-long cylindrical LCE microrobot swam back and forth in the bulk of a density matching solution at a speed of few microns per second, propelling itself by light-controlled traveling-wave deformations. Differently from the case of magnetic manipulation, the projected light only provides power and permits control of the microrobots. The actions that drive the deformation are instead generated by a light-triggered molecular re-orientation within the LCE (see Fig. 8.1), thus no external forces or torques are applied on the microrobots' body. Therefore, such soft microrobots represent the first example of a fully-artificial self-propelled microswimmer.
To achieve flexibility and adaptability comparable to those of biological ciliary propulsion, the traveling-wave deformation of the soft artificial microswimmers is not pre-programmed at the fabrication stage. Conversely, the structured light field is tuned to excite the desired deformation within the LCE microrobots, which have very simple and agnostic designs. In the case of traveling-wave deformations, the wave parameters of the body-shape change are controlled by the corresponding wave parameters of the projected light pattern. Such versatility allows a single artificial microswimmer to execute a variety of gaits on demand. In particular, we have observed that by varying the wavelength of the deformation pattern, propulsive motions mimicking the symplectic metachrony of ciliates can be changed into motions resembling, instead, antiplectic metachrony. It must be noticed that this artificial pseudo-antiplectic mode mimics antiplectic metachronal propulsion by changing the relative amplitude of the longitudinal vs. radial deformation of the LCE (the former depends on the wavelength), rather than by reversing the relative phase among beating cilia like in real antiplectic metachrony. Nonetheless, propulsive motions mimicking different kinds of ciliates' metachrony can be achieved in a single artificial microswimmer, dynamically controlled by structured light.
8.2.2.3 Versatility of artificial traveling-wave self-propulsion
In spite of the flexibility of the implemented propulsion mechanism, the wave deformation can only travel in either direction along the cylinder axis, since the self-propelled microswimmers presented above have a cylindrical shape. For this reason the LCE cylindrical microswimmers can only self-propel back and forth. To further explore the versatility of artificial traveling-wave propulsion at the micro-scale, our group has also developed microrobots in the shape of a disk, i.e. shapes that have no preferential direction of movement in a plane [13]. These microrobots consist of a LCE with a slightly different formulation and their movement was tested on the bottom surface of a liquid-filled container (we do not call them swimmers, as it is not clear whether they swim in the fluid or crawl on the surface – in both cases the propulsion is given by the traveling-wave deformation). The high symmetry of their geometry means that the disk microrobots can achieve a variety of deformation behaviors in the plane of the disk.
By using linear wave patterns traveling in different directions, the locomotion of the disk microrobots is controlled such that they can head toward any direction in a plane. In particular, linear waves propel the microrobot in the opposite direction to the induced waves. In this way, two-dimensional (2D) controlled locomotion of the microrobots is achieved, such as following a square- or diamond-shaped path. In addition, azimuthal waves rotating around the disk's axis are used to induce in-place rotation of a microrobot (in the opposite direction to the light pattern). Both kinds of locomotion (translation and rotation) can also be adjusted in terms of wave parameters. Therefore, a single microrobot can execute internal wave deformations with a variety of frequencies, wavelengths and symmetries, which in turn drive a number of different whole-body gaits. It is also possible to control several microrobots. This demonstrates the versatility that traveling-wave propulsion can achieve when the microrobots have an agnostic design and its deformation can be flexibly controlled.
8.3 Helical propellers in non-Newtonian biological media
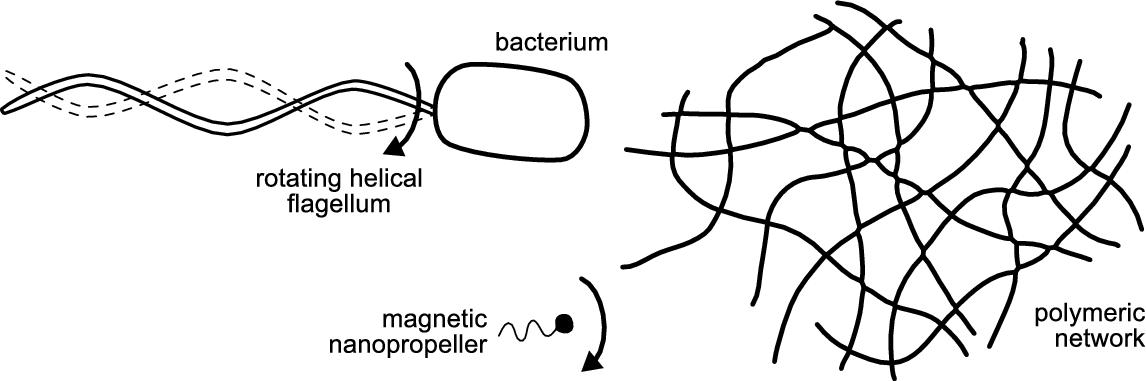
A propulsion scheme that has been adopted in the development of microrobots is the helical corkscrew propulsion used by motile bacteria (see Section 8.1 and Fig. 8.2). To this aim, various kinds of micro-scale helical propellers resembling bacterial flagella have been developed. These are usually driven by external rotating magnetic fields, and the rotation of the propeller generates thrust that pushes it forward in the fluid. Most experiments using magnetic micro-helices or comparable structures have thus far been performed in water or other Newtonian fluids [14–16]. However, for applications inside living organisms, these propellers need to be able to move through biological fluids and tissue. These tend to be much more complex rheological systems exhibiting non-Newtonian, size-dependent, and viscoelastic behaviors.
The rheological or mechanical properties of biological media are usually due to the presence of a high amount of macromolecules, cells, and/or other both colloidal and interconnected structures. Blood, for example, contains high concentrations of dispersed cells, which for a moving micro-scale agent act as rigid obstacles. Nevertheless, micropropellers have been successfully navigated in undiluted blood samples, and were found to undergo stick–slip motion [17]. However, blood is designed to flow at high velocities through narrow channels, which requires a relatively low viscosity.
Most biological media, on the other hand, often contain fluids more difficult to penetrate or deform: dense gel-like networks of interconnected polymer chains with mesh sizes in the range of tens to hundreds of nanometers [18–20]. Such media are both highly viscoelastic, and characterized by strongly size-dependent transport behavior of both molecules and nanoparticles, i.e. motion for particles larger than the mesh size is impeded, while smaller particles pass through the mesh with little resistance [21–24].
Many microorganisms are able to swim through viscoelastic polymeric solutions using a variety of propulsion mechanisms. Depending on both the swimming method and the medium, either enhancement or retardation of swimming speeds compared to Newtonian liquids can be observed [25–30]. The propulsion of artificial structures in viscoelastic solutions has also been studied, both theoretically and experimentally, although experimental studies have largely focused on macro-scale model systems [31–36]. Overall, the behavior can be complex. For instance, when moving in Boger-fluid, the force-free swimming speed of a macro-scale rigid helix can be either faster or slower than in Newtonian fluids, and factors such as the drive frequency and the elastic relaxation time of the fluid play crucial roles [31]. For heterogeneous gel-like media with a mesh size larger than the swimmer size, enhanced propulsion has been found theoretically [33,35]. This section examines physical and chemical means that can be used to move micro- and nanopropellers through complex biomedically relevant fluids and is based on previous work published [37].
8.3.1 Propulsion in hyaluronan polymer networks
Even though it has been shown that helical propulsion should, from a hydrodynamic viewpoint, result in effective forward motion in viscoelastic media, there remains a problem associated with magnetically actuated micron-scale propellers in particular, which is potentially applicable to other propulsion mechanisms as well. In biological polymer solutions, mesh entanglement results in an effective viscosity, and thus resistance, that is significantly higher than in water. Therefore the torque that can be applied with realistic laboratory magnetic fields is insufficient for effective propulsion. For example, even in relatively dilute solutions of hyaluronan, micropropellers with diameters of about 400 nm or above do not effectively move (in fields of up to 10 mT).
However, enhanced diffusion for passive nano- and microparticles below the mesh size has been previously observed in various tissues [23,38]. Furthermore, magnetic particles that are moved via gradient fields exhibit a significant increase in motility below a critical threshold size in biological fluids [39,40]. This suggests that one strategy for circumventing high macroscopic viscoelasticity is to simply reduce the propeller size to dimensions below or at least comparable to the openings in the polymer network, i.e. to the sub-micron scale (see Fig. 8.2). This poses two challenges: fabricating the complex shape and multifunctional material composition necessary at this length scale, and successfully steering the propeller in a size regime where diffusive Brownian motion typically dominates [41]. Propellers this small are of interest not only because they would be capable of effective locomotion in extracellular biological media, but they could potentially operate inside living cells or other extremely confined environments. In order to test this possibility, a well-defined non-Newtonian system is required. For this we first describe a major component of biological media, hyaluronan, which forms polymer networks.
8.3.1.1 Properties of hyaluronan
Hyaluronan, or hyaluronic acid (HA), is well suited as a model biological fluid. It is a linear polysaccharide which is formed in the cell's plasma membrane and occurs in low concentrations in almost all biological fluids and tissues. The concentration is relatively high in the synovial fluid of the joints and the vitreous of the eye, and it often contributes to a tissue's viscoelastic properties and controls hydration and water transport, among other functions [20,42–44]. It also plays important roles in processes ranging from embryogenesis and signal transduction to cancer invasiveness and metastasis [20]. HA consists of disaccharide units of N-acetyl-D-glucosamine and glucuronic acid and has a molecular mass often on the order of several MDa. A very characteristic feature of HA solutions is their high viscosity even at low concentrations. At higher concentrations HA forms a highly viscoelastic interconnected 3D transient network [21,44]. The observed pore size of the HA network in solution depends strongly on both the concentration, as well as the conditions in the solution that is being investigated, and the technique used to determine the pore size. Values between roughly 10 and 100 nm have been obtained using a variety of techniques such as probe diffusion, light scattering, electron microscopy, and NMR [21,22,45,46]. This pore structure leads to strongly size-dependent transport properties at that length-scale, and HA is therefore a good model to examine the size-dependence of micropropulsion in biological polymeric networks.
The complex viscosity of HA samples with concentrations on the order of those found in biological systems is in the range of hundreds of cP (depending on shear rate). This is several orders of magnitude higher than the viscosity of water, which explains why weak magnetic fields cannot move magnetic microrobots through many biological systems. However, these values are derived from measurements with a standard rheometer and are purely macroscopic, thus they do not reveal anything about the rheological properties at the sub-micron scale – a length scale close to the network size, where thus far no microrobots have operated. However, as we shall show, if the ‘bots’ are small enough, they can move relatively unhindered through the pores in the network. This calls for a fabrication method that can be used to realize nanorobots.
8.3.1.2 Magnetic helical nanopropellers
Magnetic micropropellers which are approximately 300 nm wide and 1.5 μm long [50] can be grown in large numbers (billions) using a physical vapor deposition (PVD) method known as glancing angle deposition (GLAD). To reduce the size of these structures even further, nanopatterning was combined with GLAD to produce magnetic nanopropellers that are only about 400 nm in length with a filament diameter around 70 nm. These results were originally reported in [37,48]. The shadow-growth technique is termed nanoGLAD, where uniform arrays of gold nanodots produced via micellar nanolithography act as a seed layer for the subsequent shadow growth PVD process [47]. For the seed layer, uniform Au nanodot arrays were produced via micellar nanolithography [49]. Silica helices containing a Ni-segment for magnetic propulsion were grown at room temperature on top of these arrays. The magnetic nickel section has a thickness of about 40 nm, and the resulting helices exhibit ferromagnetic behavior. When actuated by a rotating magnetic field in water, these nanopropellers do not show directional propulsion due to strong Brownian motion. Brownian motion might be negligible for particles tens of microns or larger, but in the size range of hundreds of nanometers, these randomizing forces need to be taken into account when describing or predicting propeller behavior. This is due to the fact that a random motion would not only be superimposed on the directional propulsion, it could also prevent alignment of the propeller with the magnetic field via rotational diffusion, in which case the particle would not be able to follow the rotation of the magnetic field, and would thus not exhibit any directional translation. Ghosh et al. performed the first numerical simulations to determine the minimum length a propeller can have before Brownian motion effects dominate such that no directional movement can be observed, and found a minimum length of about 900 nm in water [17]. In accordance with this prediction, it was found that nanohelices with a length of 400 nm show strong Brownian diffusion and no discernible propulsion in pure water.
A rigorous analytical study of the effect of randomizing Brownian forces on the propulsion behavior of micro- and nanopropellers was performed by Morozov and Leshansky [48]. This involved analytical expressions for the Péclet number for both the translational and rotational diffusion of a propeller. The Péclet number Pe is defined as the ratio of directional to diffusive motion and reflects the structure's ability to perform the kind of deterministic translational motion necessary for precise tetherless control of nanopropellers. The Péclet number can be used to determine a minimum length of the structure that depends not only on the driving frequency, but also on the viscosity of the surrounding medium, so that propulsion of very small structures can indeed be feasible if the experiments are conducted in solutions of the appropriate viscosity. This was verified experimentally by successfully navigating the nanopropellers described above in viscous glycerol–water mixtures.
In HA, the nanopropellers, as opposed to the micropropellers, show very efficient forward propulsion. This is due to the fact that their diameter is of the same size range as the mesh-size of the HA chains, thus the particles are not hindered by the polymeric network that causes the macroscopic viscoelastic properties of HA [48]. Furthermore, the propellers actually seem to experience a considerable enhancement in propulsion when moved from the viscous into the viscoelastic medium. The step-out frequency is also higher in HA solutions. Even at very high frequencies the dimensionless velocity (the propellers' velocity normalized by the helices' pitch and the driving frequency) is still significantly higher than the maximum value achieved in viscous solutions. Thus it appears that the nanoscrews do not experience the macroscopic viscosity of the polymer solution, as their step-out frequency does not decrease, which would be expected in this case. At the same time the nanopropellers retain very high directionality and show high (dimensionless) velocities. This enhanced propulsion of the nanopropellers in HA solution, in comparison with the glycerol–water mixture, is possibly a consequence of hindered pitching due to interaction of the nanopropeller with the entangled polymer mesh. This results in improved directionality by effectively improving alignment with the magnetic field and rotation around the long axis. The interaction should be particularly effective if the length of the propeller exceeds the mesh size of the entangled polymer network.
The reversal of relative efficacy between microhelices in the Newtonian medium and nanohelices in HA can be traced back to the mesh network present in biological fluids. In a Newtonian fluid, the magnetic torque applied to a particle, and the viscous drag that opposes it both scale as 
, where L is the characteristic particle size. Translational diffusion on the other hand scales as 
. The result is that in a Newtonian fluid larger particles propel with improved efficiency, i.e. higher directionality and dimensionless velocity. In the mesh network of HA and other polymers, however, the resistance to motion ζ is associated with an activation barrier determined by the elastic expansion of the mesh [22,51]. In particular, in a polymeric network ζ is proportional to the resistance in pure solvent 
and exponentially increases with the ratio between the L and the typical mesh size ψ. Since the resistance to motion grows much faster with size than the cubic term in the torque, it means that in biological fluids comprising dense networks, increasing the particle size only improves propulsion efficacy for propellers up to around the critical mesh size, and decreases again for larger particles, in agreement with experimental observations.
In summary, nanoscale magnetic propellers can be fabricated which are small enough to be controllably navigated within the macromolecular mesh of biological fluids or gels. In a hyaluronan solution, a polymeric viscoelastic gel that can be found in a large number of biological tissues, the nanohelices can be actively propelled. As opposed to larger micropropellers with a diameter of several hundred nanometers, the nanopropellers can move through HA solutions and even do so with significantly higher velocities than in Newtonian fluids. This suggests that actuated structures smaller than a certain threshold size determined by the microscopic organization of the surrounding medium may experience significantly enhanced propulsion efficiencies, which could pave the way for actively propelled “nanorobots” inside biological media and living organisms.
8.3.2 Propulsion in mucin
While there can be a significant size-effect when propelling small structures through complex biological media, the strategy employed to achieve efficient penetration of a material must naturally depend on the exact nature of both the medium and the propeller. HA is in many respects a relatively simple model of a viscoelastic biological fluid, since the polymer chains do not exhibit strong interactions with the colloidal helices. Gastric mucin, on the other hand, is known for its tendency to adsorb strongly to surfaces, a phenomenon termed muco-adhesion, and to thereby reduce particle motility [24,52]. In fact, with mucus being the first layer of defense on every surface of the body where substance exchange with the environment takes place, as for example in the airway system and gastro-intestinal tract, mucin is specifically designed to allow for the transport of small molecules like nutrients or oxygen, but prevent the penetration of micron-sized structures that include most pathogens [53,54]. It is therefore of high interest to achieve efficient propulsion in this system, and an approach to realize propulsion of microhelices with (almost) arbitrary diameter in mucus presents an important step towards eventual applications. Successful active penetration of mucus would be particularly useful if a versatile and easily adaptable strategy is employed, i.e. one that does not depend critically on particle size, and can therefore possibly be applicable to a large range of particulate delivery systems.
8.3.2.1 Motility in mucus
Mucus is a secretion which lines all epithelial surfaces which exchange substances with the environment, and therefore serves multiple functions. The most prominent function is the lubrication and hydration of epithelial cells, preventing the infiltration of pathogens, and ensuring an efficient exchange of gases and nutrients. It is usually the first barrier for drugs to enter the circulatory system, which makes its transport properties of high interest to numerous fields associated with substance/drug delivery in living organisms [53,55]. Like all biological fluids, mucus consists primarily of water, with dissolved salts, lipids, phospholipids, cholesterol, and a myriad of different proteins and enzymes. Mostly responsible for the viscoelastic gel-like properties are high molecular weight glycoproteins termed mucins [52]. These large polymers contain a protein backbone attached to which are oligosaccharide side-chains, which make up on the order of 80 wt% of the entire polymer.
The physical properties of mucin solutions vary strongly with pH. At pH 4 and below, the storage modulus 
of porcine gastric mucin (PGM) strongly exceeds the loss modulus 
, indicating an elastic gel-like material. At neutral pH, both and are orders of magnitude lower than in acidic conditions, and viscous behavior dominates over the elastic response (
), which is characteristic of a relatively low viscosity liquid [56]. The ability of artificial particles to penetrate the mucosa, however, depends not only on the fluid's macroscopic rheological properties, but also on its microrheology. This in turn is associated with the polymer network's mesh size, as well as interactions between mucin and the particles' surface [24].
Particles have been observed to diffuse more easily through mucus when treated with an appropriate surface-modification [52], due to the tendency of mucin to adhere to different surfaces. Coatings such as polyethylene glycol (PEG), various hydrophilic graft polymer chains, and adsorbed bile salts result in muco-inert surfaces that increase particle motilities [24,52,57,58]. However, while such coatings can prevent a physical immobilization of micro- and nanoparticles, it does not reduce the high viscosity of mucin gels, which still causes a significantly reduced particle diffusivity compared to fluids of lower viscosity.
The strong pH dependence of mucin's mechanical properties is exploited by the microorganism Helicobacter pylori, a flagellated pathogen that colonizes the stomach. It produces the enzyme urease, which catalyzes the hydrolysis of urea into NH3 and CO2 and consequently raises the pH of its surroundings (see Fig. 8.3). The pH increase protects the bacteria against the harsh acidic environment of the stomach. In addition it also reduces the mucus barrier's viscoelasticity, allowing H. pylori to swim through the solution and attach itself to the stomach's epithelial cells [30] where it can cause stomach ulcers. It could be shown that H. pylori bacteria are capable of moving freely through mucin solutions at neutral pH, while they are immobile in acidic mucin gels only in the absence of urea [30].
Since gastric mucus generally occurs at low pH values in the lining of the stomach, a passivation technique that stabilizes the magnetic layer against oxidation in acidic environments is one of the requirements for magnetic propulsion in this medium. It was found that micropropellers stabilized via Atomic Layer Deposition (ALD) retain their magnetic properties over extended periods of time in acidic aqueous solutions.
However, when placed in reconstituted mucin solution at neutral pH (corresponding to a low viscosity), the magnetic propellers rotate in a rotating magnetic field, but do not exhibit any forward propulsion, even at very low mucin concentrations. This can be attributed to muco-adhesion [54,57,58], i.e. the adsorption of mucin to the surface of the particles which prevents any directional movement. The theory that adhesion, rather than (or in addition to) pore size, is responsible for the immobilization of the micropropellers in mucin, is supported by the observation that the nanopropellers described in the previous section are also unable to navigate even very dilute neutral mucin solutions. To reduce muco-adhesion, various coatings and surface passivation techniques have been proposed [24,52,57,58]. However, muco-adhesion to the micropropellers could be prevented by bile salts [57]. Therefore, no covalent surface functionalization was required. It should be stressed that bile acids are present in naturally occurring stomach mucus at low concentrations [59].
8.3.2.2 Enzymatically active biomimetic micropropellers
The demonstration of an effective mimicry to penetrate mucus is based on our recent results reported in [37,60]. Mimicking the strategy of the bacterium Helicobacter pylori [30] makes use of the enzyme urease to alter the local pH value and lower the gel's viscoelasticity, to allow for propulsion through the mucus. This changes the surrounding fluid's properties reversibly, and is therefore minimally destructive to its environment. Acid-stable micropropellers can be readily functionalized with urease using a standard reaction scheme (see Fig. 8.3) [61,62]. For this the propellers are first treated with 3-aminopropyltriethoxy silane (APTES) and activated with glutaraldehyde (GA), which then allows the enzyme to be coupled to the surface. The immobilized enzyme retains a catalytic activity that is sufficient to increase the surrounding's pH and thus induce a gel–sol transition in slightly acidified mucin solutions, on a timescale appropriate for efficient forward propulsion.
It was verified that these micropropellers are indeed unable to move at acidic pH where mucin solutions form a viscoelastic gel. In solutions of 2% mucin, 1 mM bile salts, and small amounts of hydrochloric acid, no propulsion can be observed at a magnetic field strength of 10 mT. The gel state of the mucin is obvious not only in that it prevents propulsion of the helices, but in that it also reduces Brownian motion of any colloidal particles in the sample. Adding 20 mM urea does not change this observation in the case of unfunctionalized propellers, which is consistent with the finding that this small amount of urea does not interfere with the gelation behavior of mucin solutions. This in turn was also verified by macroscopic rheological measurements.
It was then tested whether micropropellers functionalized with urease are able to navigate a mucin gel by actively changing the rheological properties of the surrounding medium. Effective propulsion of urease-functionalized micropropellers was indeed observed in urea-containing acidified mucin solutions. In the absence of either urea and/or urease, these micropropellers do not move, as expected. It should be noted that the velocity observed for the micropropellers that induce a gel–sol transitions is only slightly more than half, i.e. significantly lower, than what can be observed for micropropellers moving in low-viscosity mucin control solutions (i.e. at neutral pH). The experiments clearly demonstrate that only the urease-functionalized micropropellers can actively penetrate the mucin gel, and that this active motion is only enabled in the presence of the enzyme substrate urea.
Future active microparticle systems could be even more effective if an enzyme is used that is optimized for low acidic conditions and if the enzyme is not only immobilized on the surface of the microrobot, but instead carried in larger amounts, so that the enzymes can more quickly neutralize higher amounts of acid. This could be achieved if, for instance, porous materials were used for the fabrication of the microparticles, or by immobilizing larger amounts of enzyme onto the particle surface, e.g. via branched polymer linkers or enzyme crosslinking.
In summary, microrobots can be engineered in such a way that they actively manipulate their environment and thus become mobile. This shows that strategies for the penetration of biological hydrogel barriers, which are specifically designed to hinder the transport of micron-sized structures (i.e. pathogens), can be borrowed from microorganisms. Magnetically actuated micropropellers can successfully navigate mucin gels when functionalized with urease, which allows them to induce a gel–sol-transition in the surrounding medium. This mimics the strategy by which the bacterium H. pylori achieves motility in the mucus lining of the stomach. In addition to being of interest for the further development of remotely steerable microrobots, this could also be relevant for the generation of more efficient drug and/or particle delivery systems. The approach avoids both a systemic treatment and the use of enzymes that irreversibly degrade the protective mucus lining. Thus uptake and delivery across mucosal barriers, for instance in the gastrointestinal tract, can potentially be improved even for passively diffusing drug-carriers, if they are functionalized to reversibly reduce the viscoelasticity of the mucosa.
8.4 Swimming by reciprocal motion in non-Newtonian fluids
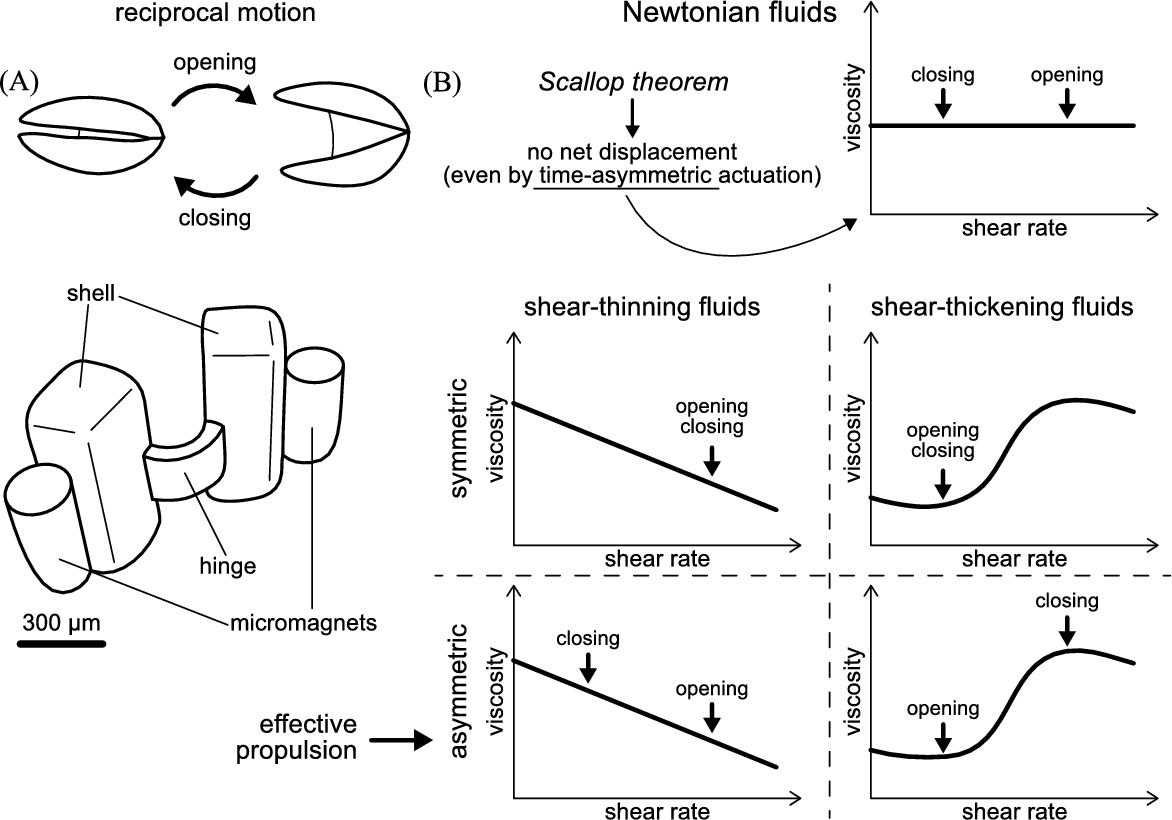
Locomotion at low Re generally requires non-reciprocal actuation of the swimmer, as described by the scallop theorem (see Section 8.1). In nature, microorganisms break time-reversal symmetry with rotating helices and cilia that show flexible oar-like beats. Inspired by nature, similar swimming strategies have been utilized to propel artificial microrobots, for example the helically-shaped propellers and the soft swimmers described in the previous sections. In order to break reciprocity, these two microrobots require relatively complex structures (fabrication processes) and/or actuation mechanisms. It is desirable to develop a non-reciprocal microswimmer with simple actuation schemes, but that can be propelled at low Re. The scallop theorem only sets the time-reversal symmetry restriction in Newtonian fluids, but not in non-Newtonian fluids where, as we show here, it can be circumvented.
In this section we describe the development of a highly symmetric single-hinge microswimmer of sub-millimeter size, namely a micro-scallop. Its opening and closing rates are externally controlled, and low-Re propulsion of the micro-scallop in shear-thickening and shear-thinning fluids is achieved by breaking time-reversal symmetry, as the speed of the opening and closing strokes differ. Excellent agreement is found between the measurements and theoretical predictions, confirming that the net propulsion is caused by the asymmetry in the apparent fluid viscosity under asymmetric shearing conditions. This section is based on previous work published in [39,63,64].
8.4.1 Development of a microswimmer propelled by reciprocal motion
8.4.1.1 Design
The design of the microswimmer is a “micro-scallop” that swims by opening and closing its shells (see Fig. 8.4). Unlike a real scallop it does not have a mouth through which it can push any fluid. Fluid enters and leaves the space between the shells from the same side. In order to achieve fast opening and closing of the scallop even in a highly viscous medium, neodymium rare earth (NdFeB) micro-magnets were attached to the shells, and the elasticity of the hinge connecting the two shells was designed to match the magnetic torque. This required a narrow (200 μm) and a thin (60 μm) hinge. However, the two shells are much thicker (300 μm) to avoid any deformation of the shells during the actuation. This ensures that the motion is indeed reciprocal. As stated by Purcell, any single-hinge structure can only exhibit reciprocal motion [2]. The two shells are also much wider than the hinge to enable a larger contact area with the fluid, which facilitates propulsion (see Fig. 8.4).
The actuation of the micro-scallop was realized by controlling the magnitude of the external magnetic field in the direction of swimming. The spatially homogeneous field applies torques on the micro-magnets, aligns the magnetic axes along the direction of the field, so as to close the two shells of the micro-scallop. The micro-magnets do not experience any pulling force by the homogeneous field, which ensures that the net displacement of the microswimmer is due to the propulsion caused by its own shape-changing swimming motions (and not due to a magnetic pulling force). The recovery stroke is provided by the internal stress in the bent elastic polymer hinge. The angle between the two shells of the micro-scallop is related to the strength of the applied external field. The asymmetric actuation of the two shells is achieved by applying sharp rises in current and hence magnetic field followed by a decay in the field.
8.4.1.2 Fabrication
The first method used to fabricate the micro-scallop is 3D printing followed by a micro-molding technique. The negative mold of the micro-scallop was printed with a high temperature material using a 3D printer (Objet260 Connex, Stratasys, Israel). The support-material was removed by magnetic stirring in KOH solution. Ultra Green Glow powder was mixed in Polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning, US). The 3D printed mold was filled with the prepared PDMS solution, degassed and cured at 65°C. Finally, the PDMS shell was released from the mold and two NdFeB micro-magnets (∅0.2 mm × 0.4 mm) were attached to the shells by an epoxy in two steps. An external magnet was used to align the two micro-magnets as seen in Fig. 8.4, as they were one after another glued to the PDMS shells.
An alternative fabrication method based on direct 3D-printing techniques was also used. Here the micro-scallop was fabricated in three steps. In the initial step, the flexible body was directly 3D-printed with a soft elastomeric material (TangoBlackPlus, Stratasys) at lower resolution (sub-mm) because of the material's large thermal expansion coefficient. Multiple bodies of the swimmer can be printed at the same time, and the printing process takes less than 10 min. Then, two micro-magnets were attached to the shells, similarly to the method described above. Finally, each microswimmer was released from the supporting material using tweezers. The 3D-printing process offers many advantages over traditional fabrication techniques, as it allows complex 3D shapes to be rapidly processed and tested and thus holds enormous potential for the fabrication of (swimming) microrobots.
8.4.1.3 Actuation set-up
The micro-scallop is not buoyant, because of the micro-magnets, and will therefore slowly sink to the bottom of a fluid container. Since the friction between the micro-scallop and the sidewalls of a container can affect its propulsion, the micro-scallop was immersed in a fluidic channel to study its swimming behavior. The width and height of the fluidic channel are 5 mm and 3 mm, respectively, which are about 8 and 4 times of the corresponding size of the micro-scallop to minimize the boundary effect of swimming at low Re. The Helmholtz coil provided a homogeneous magnetic field up to 300 G. A series of experiments with a fully submerged micro-scallop in the shear-thickening fluid were also carried out to exclude the effect of the interface on the swimming performance of the micro-scallop.
8.4.2 Propulsion in shear-thickening/thinning fluids
8.4.2.1 Non-Newtonian fluids preparation and rheological measurement
Fumed silica suspensions (8% w/w) in poly(propylene glycol) (PPG, 
, Sigma-Aldrich) were used as the shear-thickening fluid [65]. Hyaluronic acid (6 mg/mL) was used as the shear-thinning fluid. Glycerol was used as Newtonian fluids. In the shear-thickening fluid the viscosity is dominant over elasticity, which is an important point for discussing the propulsion mechanism.
8.4.2.2 Propulsion in shear-thickening fluids
Forward net displacement of the micro-scallop in a shear-thickening fluid (fumed silica in PPG) was achieved by the asymmetric actuation induced by an exponential decaying pulse signal. As a control, the micro-scallop in the same fluid was actuated with a symmetric wave-form, and, as expected, no net displacement was observed. If we take the characteristic length of the swimmer as 1 mm and the fastest linear velocity as 1000 μm/s and 100 μm/s during the fast closing and slow opening strokes, respectively, then we obtain a Reynolds number 
for the closing stroke and 
for the opening stroke, which are both much smaller than 1. Hence, the microrobot indeed swims in the regime of low Re. In each period (one opening and closing cycle), the forward displacement is larger than the backward displacement and the swimmer thus exhibits a small net displacement. After several periods a considerable net forward displacement is visible. The net displacement is only achievable under asymmetric actuation in a non-Newtonian fluid (see Fig. 8.4). The reason is that during the fast-closing half-period, the fluid in between the two shells exhibits a higher shear rate and thus a higher viscosity than the fluid in front of the swimmer; while in the slow opening half-period the viscosity there is no such difference and the fluid in front and at the back of the swimmer has a low viscosity, thus the microrobot propels further forward than backward.
8.4.2.3 Propulsion in shear-thinning fluids
Propulsion of the micro-scallop operated with a reciprocal but asymmetric actuation sequence is also achieved in a non-Newtonian shear-thinning solution of hyaluronic acid (HA), which is found in a number of biological media (see also Section 8.3.1.1), including saliva, blood, vitreous and synovial fluid [66]. An entangled polymer network typically exhibits shear-thinning behavior, as the rheology is controlled by the rate of entanglement formation and disruption. At low shear rates, the two rates are comparable and the total number of entanglements is almost constant, thus the apparent viscosity remains almost constant; when the shear rate increases, the rate of disruption becomes dominant and results in a shear-thinning effect [67]. As we show here, this property can be exploited in the design and operation of a microswimmer that is simpler to operate than most other existing microrobots.
In the shear-thinning fluid the micro-scallop only moves forward when the opening–closing cycle is opposite to that used in the shear-thickening fluid. Now, a fast-opening followed by a slow-closing step give forward propulsion (see Fig. 8.4). Again, we track the scallop's position when it is closed (minimum opening angle) and plot the trajectory of the hinge's midpoint as a function of time. As a control, the micro-scallop showed no significant forward displacement when the opening and closing cycles were symmetric, as is expected.
8.4.3 Discussion on reciprocal swimming in non-Newtonian fluids
In this section, the basis for the low-Re propulsion of a symmetric microswimmer in shear-thickening and shear-thinning fluids is discussed. Differences in the opening and closing rates give rise to differences in the corresponding shear rates and hence differences in the viscosities of the non-Newtonian fluid. The latter is shown to result in net forward locomotion. Such a mechanism is absent in Newtonian fluids, where the scallop theorem forbids the locomotion of a reciprocal swimmer. In summary, at least three conditions need to be fulfilled to swim with a single hinge microrobot by reciprocal motion at low Re. First, the fluid has to be non-Newtonian, since the same asymmetric actuation in a Newtonian fluid results in no net displacement, in accordance with Purcell's scallop theorem [2]. Second, the actuation of the swimmer needs to be coupled to a shear-rate dependent fluid. If the actuation is symmetric, then the viscosity does not change and the forward and backward displacements are equal with no net displacement. Third, a clear fore-aft asymmetry in the microrobot is also necessary for the determination of the swimming direction. In the experiment, it is demonstrated that the smaller shear rate and viscosity is in the front and the larger shear rate and viscosity at the back of the microrobot.
We found that the average velocity of the micro-scallop in the shear-thickening fluid is faster than that in the shear-thinning one, because for the same difference in shear rates the change in fluid viscosity is larger in the shear-thickening fluid. This also follows from a theoretical power law model. The swimming velocity can be increased by maximizing the difference between the opening and closing speeds, but this may not be practical. Another aspect is to optimize the shape of the swimmer. The viscosity is highly dependent on the shear rate, which is not only determined by the speed of opening and closing, but is also a function of the swimmer shape. Optimizing the shape of the swimmer (and the morphology of its surfaces) may thus have a significant effect on propulsion speed of a non-Newtonian microswimmer. The microrobot described herein is actuated by an external magnetic field, but the principle we demonstrate here – that in non-Newtonian fluids reciprocal actuators can be used for swimming – is general. It means that most micro-actuators, for example, a bimetallic strip, shape memory alloy, or any heat/light actuated polymer can be used to propel microrobots. Based on the principle described herein, new microrobots can be developed to move in non-Newtonian fluids, which include most biomedically relevant fluids.
8.5 Conclusions
Microorganisms manage to swim in water with high versatility and efficiency. Realizing this level of sophistication at such a small scale in abiotic microrobots is a formidable challenge. Furthermore, microorganisms not only swim in water, but they also exploit an impressive array of physical and chemical strategies in order to move in tissue and biological fluids. This is of interest for the development of untethered microrobots that are envisioned to have an array of potential medical applications, including targeted delivery. Biological media are inhomogeneous and are characterized by a complex structure and non-Newtonian rheological properties. Unlike water, biomedically important fluid systems therefore possess shear- and size-dependent properties. As we show in this chapter, this not only presents a challenge for artificial micro- and nanorobots, but also opportunities for novel propulsion mechanisms. Specifically, we discuss three microrobotic and one nanorobotic system that we have recently developed and that either mimic microorganisms to swim or use completely new propulsion schemes to move in biological media (Fig. 8.5).
We first discuss a soft microrobot which swims with the wave-like propulsion mechanism of ciliates. It consists of an elastomeric body that can be actuated by light. This “photobot” is a true swimmer, as it swims only due to body shape changes. Its body is unstructured, but since its deformation can be dynamically excited by a light pattern, it can exhibit a very large number of potential deformations and thus it mimics some of the flexibility of ciliated microorganisms. We also discuss a system of rigid magnetic flagella that can be grown in very large numbers (billions) and that are propelled through solution with a corkscrew-like mechanism. A strategy for the penetration of biological media is to fabricate nanopropellers that are so small that they can move unhindered through the macromolecular network found in biological fluids and tissue. These nanorobots are smaller than any swimming microorganism. We also discuss a chemical strategy to penetrate mucus that is used by the bacterium H. pylori. To mimic this, artificial micropropellers are functionalized with the enzyme urease such that they locally increase the pH and thus turn an otherwise impenetrable gel into a fluid. Finally, we show that an abiotic “micro-scallop”, that does not have a direct biological analogue, can move by opening and closing its rigid shells. It cannot swim in water because its motion is reciprocal, but it swims in non-Newtonian fluids. Since from an engineering point of view reciprocal motion can be achieved with much simpler actuation schemes compared to non-reciprocal actuators, this microrobot suggests new possibilities in designing biomedical micro-devices.
We have shown that in order to develop new microswimmers and microrobots at very small scales, including those that can operate in biological fluids and tissues, it is important to carefully take into account the physics and the chemical nature of the target medium. Whereas swimming in Newtonian fluids requires complex non-reciprocal motions, such as traveling-wave deformations, reciprocal motions can actually be propulsive in non-Newtonian fluids. Movement in gel-like media can be achieved through different strategies, either physical or chemical, depending on the molecular structure of the medium or tissue. It is also advantageous to adopt strategies that pathogens have developed to effectively move in and through biological media. We expect that the approach we demonstrate here will lead to new microswimmers and microrobots and therefore to a number of biomedical applications.