Chapter 3
Accelerated Many-Core GPU Computing for Physics and Astrophysics on Three Continents
3.1 INTRODUCTION
Theoretical numerical modeling has become a third pillar of sciences in addition to theory and experiment (in the case of astrophysics, the experiment is mostly substituted by observations). Numerical modeling allows one to compare theory with experimental or observational data in unprecedented detail, and it also provides theoretical insight into physical processes at work in complex systems. Similarly, data processing (e.g., of astrophysical observations) comprises the use of complex software pipelines to bring raw data into a form digestible for observational astronomers and ready for exchange and publication; these are, for example, mathematical transformations like Fourier analyses of time series or spatial structures, complex template analyses, or huge matrix–vector operations. Here, fast access to and transmission of data, too, require supercomputing capacities. However, sufficient resolution of multiscale physical processes still poses a formidable challenge, such as in the examples of few-body correlations in large astrophysical many-body systems or in the case of turbulence in physical and astrophysical flows.
We are undergoing a new revolution on parallel processor technologies, and a change in parallel programming paradigms, which may help to advance current software toward the exaflop scale and to better resolve and understand typical multiscale problems. The current revolution in parallel programming has been mostly catalyzed by the use of graphical processing units (GPUs) for general-purpose computing, but it is not clear whether this will remain the case in the future. GPUs have become widely used nowadays to accelerate a broad range of applications, including computational physics and astrophysics, image/video processing, engineering simulations, and quantum chemistry, just to name a few. GPUs are rapidly emerging as a powerful and cost-effective platform for high-performance parallel computing. The GPU Technology Conference 2010 held by NVIDIA in San Jose in autumn 20101 gave one snapshot of the breadth and depth of present-day GPU (super)computing applications. Recent GPUs, such as the NVIDIA Fermi C2050 Computing Processor, offer 448 processor cores and extremely fast on-chip-memory chip, as compared to only four to eight cores on a standard Intel or AMD central processing unit (CPU). Groups of cores have access to very fast shared memory pieces; a single Fermi C2050 device supports double-precision operations fully with a peak speed of 515 gigaflops; in this chapter, we also present results obtained from GPU clusters with previous generations of GPU accelerators, which have no (Tesla C870) or only very limited (Tesla C1060) double-precision support. We circumvented this by emulation of a few critical double-precision operations (Nitadori and Makino, 2008). More details can be found in the PhD thesis of one of us (K. Nitadori), “New Approaches to High-Performance N-Body Simulations with High-Order Integrator, New Parallel Algorithm, and Efficient Use of SIMD Hardware,” University of Tokyo, in 2009.
Scientists are using GPUs since more than 5 years already for scientific simulations, but only the invention of CUDA (Akeley et al., 2007; Hwu, 2011) as a high-level programming language for GPUs made their computing power available to any student or researcher with normal scientific programming skills. CUDA is presently limited to GPU devices of NVIDIA, but the open source language OpenCL will provide access to any type of many-core accelerator through an abstract programming language. Computational physics and astrophysics has been a pioneer in using GPUs for high-performance general-purpose computing (e.g., see the early AstroGPU workshop in Princeton 2007) through the information base.2 Astrophysicists had an early start in the field through the Gravity Pipe (GRAPE) accelerator boards from Japan from 10 years ago (Makino et al., 2003; Fukushige et al., 2005). Clusters with accelerator hardware (GRAPE or GPU) have been used for gravitating many-body simulations to model the dynamics of galaxies and galactic nuclei with supermassive black holes (SMBHs) in galactic nuclei (Berczik et al., 2005, 2006; Berentzen et al., 2009; Just et al., 2011; Pasetto et al., 2011), in the dynamics of dense star clusters (Hamada and Iitaka, 2007; Portegies Zwart et al., 2007; Belleman et al., 2008), in gravitational lensing ray shooting problems (Thompson et al., 2010), in numerical hydrodynamics with adaptive mesh refinement (Wang and Abel, 2009; Schive et al., 2010; Wang et al., 2010a), in magnetohydrodynamics (Wong et al., 2009), or fast Fourier transform (FFT) (Cui et al., 2009). While it is relatively simple to obtain good performance with one or few GPUs relative to the CPU, a new taxonomy of parallel algorithms is needed for parallel clusters with many GPUs (Barsdell et al., 2010). Only “embarrassingly” parallel codes scale well even for large number of GPUs, while in other cases like hydrodynamics or FFT on GPU, the speedup is somewhat limited to 10–50 for the whole application, and this number needs to be carefully checked whether it compares the GPU performance with single or multicore CPUs. A careful study of the algorithms and their data flow and data patterns is useful and has led to significant improvements, for example, for particle-based simulations using smoothed particle hydrodynamics (SPH) (Berczik et al., 2007; Spurzem et al., 2009) or for FFT (Cui et al., 2009). Recently, new GPU implementations of fast-multipole methods (FMMs) have been presented and compared to Tree Codes (Yokota and Barba, 2010; Yokota et al., 2010). FMM codes have first been presented by Greengard and Rokhlin (1987). It is expected that on the path to exascale applications, further—possibly dramatic—changes in algorithms are required; at present, it is unclear whether the current paradigm of heterogeneous computing with a CPU and an accelerator device like GPU will remain dominant.
While the use of many-core accelerators is strongly growing in a large number of scientific and engineering fields, there are still only few codes able to fully harvest the computational power of parallel supercomputers with many GPU devices, as they have recently become operational in particular (but not restricted to) in China. In China, GPU computing is blooming; the top and third spots in the list of 500 fastest supercomputers in the world3 are now occupied by Chinese GPU clusters, and one of the GPU clusters used for results in this chapter is on rank number 28 (Mole-8.5 computer; see next discussion and Wang et al., 2010b). In this chapter, we present in some detail an astrophysical N-body application for star clusters and galactic nuclei and star clusters, which is currently our mostly well-tested and also heavily used application. Furthermore, somewhat less detailed, we present other applications scaling equally very well, such as an adaptive mesh refinement hydrodynamic code, using (among other parts) an FFT and relaxation methods to solve Poisson’s equation, and give some overview on physical and process engineering simulations.
3.2 ASTROPHYSICAL APPLICATION FOR STAR CLUSTERS AND GALACTIC NUCLEI
Dynamical modeling of dense star clusters with and without massive black holes poses extraordinary physical and numerical challenges; one of them is that gravity cannot be shielded, such as electromagnetic forces in plasmas; therefore, long-range interactions go across the entire system and couple nonlinearly with small scales; high-order integration schemes and direct force computations for large numbers of particles have to be used to properly resolve all physical processes in the system. On small scales, correlations inevitably form already early during the process of star formation in a molecular cloud. Such systems are dynamically extremely rich; they exhibit a strong sensitivity to initial conditions and regions of phase space with deterministic chaos.
After merging two galaxies in the course of cosmological structure formation, we start our simulations with two SMBHs embedded in a dense star cluster, separated by some 1000 pc (1 pc, 1 parsec, about 3.26 light years, or 3.0857·1018 cm). This is a typical separation still accessible to astrophysical observations (Komossa et al., 2003). Nearly every galaxy harbors an SMBH, and galaxies build up from small to large ones in a hierarchical manner through mergers following close gravitational encounters. However, the number of binary black holes observed is relatively small, so there should be some mechanism by which they get close enough to each other to coalesce under emission of gravitational wave emission. Direct numerical simulations of Einstein’s field equations start usually at a black hole separation in the order of 10–50 Schwarzschild radii, which is, for an example of a 1 million solar mass black hole (similar to the one in our own galactic center), about 10−5 pc. Therefore, in order to obtain a merger, about eight orders of magnitude in separation need to be bridged. In our recent models, we follow in one coherent direct N-body simulation how interactions with stars of a surrounding nuclear star cluster, combined with the onset of relativistic effects, lead to a black hole coalescence in galactic nuclei after an astrophysically modest time of order 108 years (Berentzen et al., 2009; Preto et al., 2011). Corresponding to the multiscale nature of the problem in space, we have a large range of timescales to be covered accurately and efficiently in the simulation. Orbital times of SMBHs in galactic nuclei after galactic mergers are of the order of several million years; in the interaction phase with single stars, the orbital time of a gravitationally bound supermassive binary black hole goes down to some 100 years—at this moment, there is a first chance to detect its gravitational wave emission through their influence on pulsar timing (Lee et al., 2011). Energy loss due to Newtonian interactions with field stars interplays with energy loss due to gravitational radiation emission; the latter becomes dominant in the final phase (at smaller separations) when the black hole binary enters the wave band of the planned laser interferometer space antenna (LISA4), where one reaches 0.01-Hz orbital frequency. Similarly, in a globular star cluster, timescales can vary between a million years (for an orbit time in the cluster) to hours (orbital time of the most compact binaries). The nature of gravity favors such strong structuring properties since there is no global dynamic equilibrium. Gravitationally bound subsystems (binaries) tend to exchange energy with the surrounding stellar system in a way that increases their binding energy, thus moving further away from a global equilibrium state. This behavior can be understood in terms of self-gravitating gas spheres undergoing gravothermal catastrophe (Lynden-Bell and Wood, 1968), but it occurs in real star clusters on all scales. Such kind of stellar systems, sometimes called dense or gravothermal stellar systems, demands special high-accuracy integrators due to secular instability, deterministic chaos, and strong multiscale behavior. Direct high-order N-body integrators for this type of astrophysical problem have been developed by Aarseth (see for reference Aarseth, 1999b, 2003). They employ fourth-order time integration using a Hermite scheme, hierarchically blocked individual particle time steps, an Ahmad–Cohen neighbor scheme, and regularization of close, few-body systems.
Direct N-Body Codes in astrophysical applications for galactic nuclei, galactic dynamics, and star cluster dynamics usually have a kernel in which direct particle–particle forces are evaluated. Gravity as a monopole force cannot be shielded on large distances, so astrophysical structures develop high-density contrasts. High-density regions created by gravitational collapse coexist with low-density fields, as is known from structure formation in the universe or the turbulent structure of the interstellar medium. A high-order time integrator in connection with individual, hierarchically blocked time steps for particles in a direct N-body simulation provides the best compromise between accuracy, efficiency, and scalability (Makino and Hut, 1988; Spurzem, 1999; Aarseth, 1999a, 1999b; Harfst et al., 2007). With GPU hardware, up to a few million bodies could be reached for our models (Berczik et al., 2005, 2006; Gualandris and Merritt, 2008). Note that while Greengard and Rokhlin (1987) already mentioned that their algorithm can be used to compute gravitational forces between particles to high accuracy, Makino and Hut (1988) found that the self-adaptive hierarchical time-step structure inherited from Aarseth’s codes improves the performance for spatially structured systems by C (N)it means that, at least, for astrophysical applications with high-density contrast, FMM is not a priori more efficient than direct N-body (which sometimes is called “brute force,” but that should only be used if a shared time step is used, which is not the case in our codes). One could explain this result by comparing the efficient spatial decomposition of forces (in FMM, using a simple shared time step) with the equally efficient temporal decomposition (in direct N-body, using a simple spatial force calculation).
On the other hand, cosmological N-body simulations use thousand times more particles (billions, order of 109), at the price of allowing less accuracy for the gravitational force evaluations, either through the use of a hierarchical decomposition of particle forces in time (Ahmad and Cohen, 1973; Makino and Aarseth, 1992; Aarseth, 2003) or in space (Barnes and Hut, 1986; Makino, 2004; Springel, 2005). Another possibility is the use of fast-multipole algorithms (Greengard and Rokhlin, 1987; Dehnen, 2000, 2002; Yokota and Barba, 2010; Yokota et al., 2010) or particle–mesh (PM) schemes (Hockney and Eastwood, 1988; Fellhauer et al., 2000), which use FFT for their Poisson solver. PM schemes are the fastest for large systems, but their resolution is limited to the grid cell size. Adaptive codes use direct particle–particle forces for close interactions below grid resolution (Couchman et al., 1995; Pearce and Couchman, 1997). But for astrophysical systems with high-density contrasts, tree codes are more efficient. Recent codes for massively parallel supercomputers try to provide adaptive schemes using both tree and PM, such as the well-known GADGET and TreePM codes (Xu, 1995; Springel, 2005; Yoshikawa and Fukushige, 2005; Ishiyama et al., 2009).
3.3 HARDWARE
We present results obtained from GPU clusters using NVIDIA Tesla C1060 cards in Beijing, China (Laohu cluster with 85 Dual Intel Xeon nodes and with 170 GPUs); NVIDIA Fermi C2050 cards also in Beijing, China (Mole-8.5 cluster with 372 dual Xeon nodes, most of which have 6 GPUs, delivering in total 2000 Fermi Tesla C2050 GPUs); in Heidelberg, Germany, using NVIDIA Tesla C870 (pre-Fermi single-precision-only generation) cards (Kolob cluster with 40 Dual Intel Xeon nodes and with 40 GPUs.); and Berkeley at NERSC/LBNL using again the NVIDIA Fermi Tesla C2050 cards (Dirac cluster with 40 GPUs) (Fig. 3.1).
Figure 3.1 Left: NAOC GPU cluster in Beijing, 85 nodes with 170 NVIDIA Tesla C1060 GPUs, 170-teraflop hardware peak speed, installed in 2010. Right: Frontier Kolob cluster at ZITI Mannheim, 40 nodes with 40 NVIDIA Tesla C870 GPU accelerators, 17-teraflop hardware peak speed, installed in 2008.

In Germany, at Heidelberg University, our teams have operated a many-core accelerated cluster using the GRAPE hardware for many years (Spurzem et al., 2004, 2007, 2008; Harfst et al., 2007). We have in the meantime migrated from GRAPE to GPU (and also partly FPGA) clusters (Spurzem et al., 2009, 2010, 2011), and part of our team is now based at the National Astronomical Observatories of China (NAOC) of the Chinese Academy of Sciences (CAS) in Beijing. NAOC is part of a GPU cluster network covering 10 institutions of CAS, aiming for high-performance scientific applications in a cross-disciplinary way. The top-level cluster in this network is the recently installed Mole-8.5 cluster at the Institute of Process Engineering of the Chinese Academy of Sciences (IPE/CAS) in Beijing (2-petaflop single-precision peak), from which we also show some preliminary benchmarks. The entire CAS GPU cluster network has a total capacity of nearly 5-petaflop single-precision peak. In China, GPU computing is blooming; the top and third spots in the list of 500 fastest supercomputers in the world5 are now occupied by Chinese GPU clusters. The top system in the CAS GPU cluster network is currently number 28 (Mole-8.5 at IPE). Research and teaching in CAS institutions is focused on broadening the computational science base to use the clusters for supercomputing in basic and applied sciences.
3.4 SOFTWARE
The test code that we use for benchmarking on our clusters is a direct N-body simulation code for astrophysics, using a high-order Hermite integration scheme and individual block time steps (the code supports time integration of particle orbits with fourth-, sixth, and eighth-order schemes). The code is called φGPU; it has been developed from our earlier published versions φGRAPE (Harfst et al., 2007). It is parallelized using Message Passing Interface (MPI) and, on each node, using many cores of the special hardware. The code was mainly developed and tested by K. Nitadori and P. Berczik (see also Hamada and Iitaka, 2007) and is based on an earlier version for GRAPE clusters (Harfst et al., 2007). The code is written in C++ and is based on Nitadori and Makino (2008) an earlier CPU serial code (yebisu).
We used and tested the present version of the φGPU code only with the recent GNU compilers (version 4.x). For all results shown here, we used a Plummer-type gravitational potential softening, ε = 10−4, in units of the virial radius. More details will be published in an upcoming publication (Berczik et al., 2011).
The MPI parallelization was carried out in the same “j” particle parallelization mode as in the earlier φGRAPE code (Harfst et al., 2007). The particles were divided equally between the working nodes and in each node, we calculated only the fractional forces for the active “i” particles at the current time step. Due to the hierarchical block time-step scheme, the number Nact of active particles (due for a new force computation at a given time level) is usually small compared to the total particle number N, but its actual value can vary from 1 … N. We obtained the full forces from all the particles acting on the active particles after using the global MPI_SUM communication routines.
We used native GPU support and direct code access to the GPU with only CUDA. Recently, we used the latest CUDA 3.2 (but the code was developed and working also with the “older” CUDA compilers and libraries). Multi-GPU support is achieved through MPI parallelization; each MPI process uses only a single GPU, but we can start two MPI processes per node (to use effectively, e.g., the dual quad core CPUs and the two GPUs in the NAOC cluster) and in this case each, MPI process uses its own GPU inside the node. Communication always (even for the processes inside one node) works via MPI. We do not use any of the possible OMP (multithread) features of recent gcc 4.x compilers inside one node.
3.5 RESULTS OF BENCHMARKS
Figures 3.2 and 3.3 show results of our benchmarks. In the case of Laohu, we use maximum 164 GPU cards (three nodes; i.e., six cards were down during the test period). Here, the largest performance was reached for 6 million particles, with 51.2 teraflops in total sustained speed for our application code, in an astrophysical run of a Plummer star cluster model, simulating one physical time unit (about one-third of the orbital time at the half-mass radius). Based on these results, we see that we get a sustained speed for 1 NVIDIA Tesla C1060 GPU card of 360 gigaflops (i.e., about one-third of the theoretical hardware peak speed of 1 teraflop). Equivalently, for the smaller and older Kolob cluster with 40 NVIDIA Tesla C870 GPUs in Germany, we obtain 6.5 teraflops (with 4 million particles). This is 160 gigaflops per card.
Figure 3.2 Strong scaling for different problem sizes. Left: Dirac Fermi Tesla C2050 GPU system at NERSC/LBNL, almost 18 teraflops reached for 1 million particles on 40 GPUs. Each line corresponds to a different problem size (particle number), which is given in the key. Note that the linear curve corresponds to ideal scaling. Right: same benchmark simulations, but for the Mole-8.5 GPU cluster at IPE in Beijing, using up to 512 Fermi Tesla C2050 GPUs, reaching a sustained speed of 130 teraflops (for 2 million particles). If one would use all 2000 GPUs on the system, a sustained speed of more than 0.4 petaflop is feasible. This is the subject of ongoing present and future work.
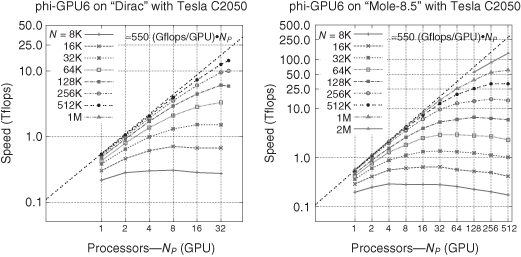
Figure 3.3 Left: Same benchmark simulations as in Figure 3.2, but for the Frontier Kolob cluster with Tesla C870 GPUs at University of Heidelberg; 6.5 teraflops reached for 4 million particles on 40 GPUs. Right: NAOC GPU cluster in Beijing; speed in teraflops reached as a function of the number of processes, each process with one GPU; 51.2 teraflops sustained were reached with 164 GPUs (three nodes with 6 GPUs were down at the time of testing).
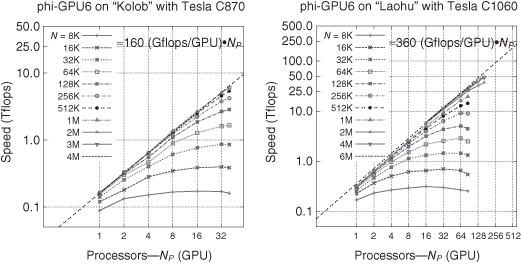
On the new clusters Dirac and Mole-8.5, where we used the NVIDIA Fermi Tesla C2050 cards, we get the maximum performance of 550 gigaflops per card. We achieve the absolute record in the performance on a Mole-8.5 cluster when we run our test simulation (even for a relatively “low” particle number—2 million) on 512 nodes and get over the 130-teraflop total performance. In principle, for a larger particle number (in the order of 10 million), we see that the maximum performance that we can get on the whole cluster (on ≈ 2000 GPUs) is around 0.4 petaflop.
We have presented exemplary implementations of direct gravitating N-body simulations and an adaptive mesh hydrodynamics code with self-gravity (Schive et al., 2010) using large GPU clusters in China and elsewhere. The overall parallelization efficiency of our codes is very good. It is about 30% of the GPU peak speed in Figure 3.2 for the embarrassingly parallel direct N-body code and still significant (in the order of 20–40 speedups for each GPU) for adaptive mesh hydrodynamic simulations. The larger N-body simulations (several million particles) show nearly ideal strong scaling (linear relation between speed and number of GPUs) up to our present maximum number of nearly 170 GPUs—no strong sign of a turnover yet due to communication or other latencies. Therefore, we are currently testing the code implementation on much larger GPU clusters, such as the Mole-8.5 of IPE/CAS.
The wall clock time T needed for our particle-based algorithm to advance the simulation by a certain physical time (usually one crossing time units) integration interval scales as
(3.1)
![]()
where the components of T are (from left to right) the computing time spent on the host, on the GPU, the communication time to send data between the host and GPU, and the communication time for MPI data exchange between the nodes. In our present implementation, all components are blocking, so there is no hiding of communication. This will be improved in further code versions, but for now, it eases profiling (Table 3.1).
TABLE 3.1 Properties of the Fermi GPU Cluster at the Institute of Process Engineering of the Chinese Academy of Sciences (IPE/CAS)
| Data of the Mole-8.5 System | |
| Item | Quantity |
| Peak performance single precision | 2 petaflops |
| Peak performance double precision | 1 petaflop |
| Linpack sustained performance | 207.3 teraflops |
| Megaflops per watt | 431 |
| Number of nodes/number of GPUs (type) | 372/2000 (Fermi Tesla C2050) |
| Total memory RAM | 17.8 terabytes |
| Total memory VRAM | 6.5 terabytes |
| Total hard disk | 720 terabytes |
| Management communication | H3C Gigabit Ethernet |
| Message passing communication | Mellanox InfiniBand Quad Data Rate |
| Occupied area | 150 m2 |
| Weight | 12.6 tons |
| Max power | 600 kW (computing) |
| 200 kW (cooling) | |
| Operating system | CentOS 5.4, PBS |
| Monitor | Ganglia, GPU monitoring |
| Languages | C, C++;, CUDA |
This system is the largest GPU cluster in Beijing, the third Chinese cluster, with rank 28 in the worldwide Top500 list (as of November 2010). It has been used for some of our N-body benchmarks, especially for the timing model, and by the physics simulations at IPE. Note that it has a relatively large number of GPUs per node, but our communication performance was not significantly affected (see comparison plots with Dirac cluster in Berkeley, which has only one GPU per node).
In the case of the φGPU code (as in the other direct NBODY codes discussed next), we used the blocked hierarchical individual time-step scheme (HITS) and a Hermite high-order time integration scheme of at least the fourth order for the integration of the equation of motions for all particles (Makino and Aarseth, 1992). In the case of HITS in every individual time steps, we integrate the motion only for s particles, a number that is usually much less compared to the total number of particles N. Its average value 〈s〉 depends on the details of the algorithm and on the particle configuration integrated. According to a simple theoretical estimate, it is 〈s〉 ∝ N2/3 (Makino, 1991), but the real value of the exponent deviates from two-thirds, depending on the initial model and details of the time-step choice (Makino and Hut, 1988).
We use a detailed timing model for the determination of the wall clock time needed for different components of our code on CPU and GPU, which is then fitted to the measured timing data. Its full definition is given in Table 3.2.
TABLE 3.2 Breaking Down the Computational Tasks in A Parallel Direct N-Body Code with Individual Hierarchical Block Time Steps
| Components in Our Timing Model for Direct N-Body Code | ||
| Task | Expected Scaling | Timing Variable |
| Active particle determination | C(s log[s]) | Thost |
| All particle prediction | C(N/NGPU) | Thost |
| “j” part. send. to GPU | C(N/NGPU) | Tcomm |
| “i” part. send. to GPU | C(s) | Tcomm |
| Force computation on GPU | C(Ns/NGPU) | TGPU |
| Receive the force from GPU | C(s) | Tcomm |
| MPI global communication | C((τlat +; s)log(NGPU)) | TMPI |
| Correction/advancing “i” particle | C(s) | Thost |
At every block time-step level, we denote s ≤ N particles, which should be advanced by the high-order corrector as active or “i” particles, while the field particles, which exert forces on the i particles to be computed, are denoted as “j” particles. Note that the number of j particles in our present code is always N (full particle number), but in more advanced codes like NBODY6 discussed next, the Ahmad–Cohen neighbor scheme uses a much smaller number of j particles for the more frequent neighbor force calculation. We also have timing components for low-order prediction of all j particles and distinguish communication of data from host to GPU and return, and through the MPI message passing network.
In practice, we see that only three terms play any relevant role to understand the strong and weak scaling behavior of our code. These are the force computation time (on GPU) TGPU and the message passing communication time TMPI, within which we can distinguish a bandwidth-dependent part (scaling as s log(NGPU)) and a latency-dependent part (scaling as τlat log(NGPU)); the latency is only relevant for a downturn of efficiency for strong scaling at a relatively large NGPU. Starting in the strong scaling curves from the dominant term at a small NGPU, there is a linearly rising part, as one can see, in all curves in Figures 3.2–3.4 (most clearly in Fig. 3.4), which corresponds only to the force computation on GPU, while the turnover to a flat curve is dominated by the MPI communication time between the computing nodes, TMPI.
Figure 3.4 Left: The Mole-8.5 Cluster at the Institute of Process Engineering in Beijing. It consists of 372 nodes, most with 6 Fermi Tesla C2050 GPUs. Right: single node of Mole-8.5 system
(courtesy of IPE, photos by Xianfeng He).

To find a model for our measurements, we use the ansatz,
(3.2)
![]()
where T is the computational wall clock time needed. For one block step, the total number of floating point operations is γ〈s〉N, where γ defines how many floating point operations our particular Hermite scheme requires per particle per step, and we have
where Ts is the computing time needed for one average block step in time (advancing 〈s〉 particles). The reader with interest in more detail how this formula can be theoretically derived for general-purpose parallel computers is referred to Dorband et al. (2003). α, β, and τlat are hardware time constants for the floating point calculation on GPU, for the bandwidth of the interconnect hardware used for message passing and its latency, respectively.
Our timing measurements are done for an integration over one physical time unit in normalized units (t = 1, which is equivalent to approximately one-third of a particle’s orbital crossing time at the half-mass radius), so it is more convenient to multiply the numerator and denominator of Equation 3.3 with the average number 〈n〉 of steps required for an integration over a physical timescale t; it is 〈n〉 ∝ t/〈dt〉, where 〈dt〉 is the average individual time step. In a simple theoretical model, our code should asymptotically scale with N2, so we would expect N〈s〉〈n〉 ∝ N2. However, our measurements deliver a slightly less favorable number 〈s〉〈n〉 ∝ N1+x, with x = 0.31, a value in accord with the results of Makino and Hut (1988). Hence, we get for the integration over one time unit
(3.4)
![]()
The parameter x = 0.31 is a particular result for our case of the sixth-order HITS and the particular initial model used for the N-body system, Plummer’s model as in Makino and Hut (1988). x is empirically determined from our timing measurements as shown in Figure 3.5. The parameters α, β, γ, and τlat can be determined as well for each particular hardware used. The timing formula can then be used to approximate our code calculation “speed” for any other number of particles, GPUs, or different hardware parameters. For example, on the Mole-8.5 system, we see that for N = 10 m particles, if we are using 2000 GPU cards on the system, we expect to get ≈ 390 teraflops (compare with Fig. 3.5). If we use our scaling formula for the much higher node-to-node bandwidth of the Tianhe-1 system at Tianjin Supercomputing Center (this is the number one supercomputer according to the Top500 list of November 2010, with 7000 NVIDIA Fermi Tesla GPUs and 160 gigabit/s node-to-node bandwidth), we can possibly reach a sustained performance on the order of petaflops. This is the subject of future research.
Figure 3.5 Strong scaling for different problem sizes on a Mole-8.5 cluster. Each line corresponds to a different problem size (particle number), which is given in the key. The sequence of lines in the plot corresponds to the sequence of lines in the key (from top to bottom). Thicker lines with dots or symbols are obtained from our timing measurements. Thinner lines show the extrapolation for larger NGPU and for larger N according to our timing model. As one can see, we reach 550 gigaflops per GPU card, in total on 512 GPUs about 280-teraflop sustained code performance for our code. An extrapolation to 2000 GPUs shows we can reach 390 teraflops on Mole-8.5 for 10 million particles.
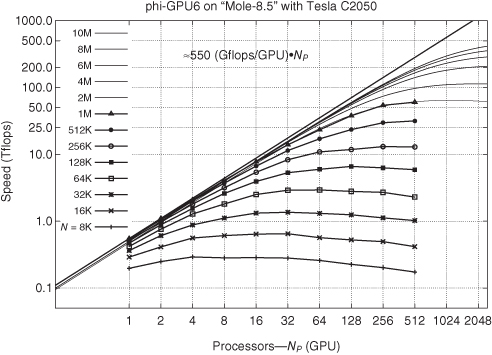
To our knowledge, the direct N-body simulation with 6 million bodies in the framework of a so-called Aarseth style code (Hermite scheme, sixth order, hierarchical block time step, integrating an astrophysically relevant Plummer model with a core–halo structure in density for a certain physical time) is the largest of such simulations that exists so far. However, the presently used parallel MPI-CUDA GPU code φGPU is on the algorithmic level of NBODY1 (Aarseth, 1999b); though it is already strongly used in production, useful features such as regularization of few-body encounters and an Ahmad–Cohen neighbor scheme (Ahmad and Cohen, 1973) are not yet implemented. Only with those the code would be equivalent to NBODY6, which is the most efficient code for single workstations (Aarseth, 1999b, 2003), eventually with acceleration on a single node by one or two GPUs (work by Aarseth & Nitadori; see NBODY66). NBODY6++ (Spurzem, 1999) is a massively parallel code corresponding to NBODY6 for general-purpose parallel computers. An NBODY6++ variant using many GPUs in a cluster is work in progress. Such a code could potentially reach the same physical integration time (with same accuracy) using only one order of magnitude less floating point operations. The NBODY6 codes are algorithmically more efficient than φGPU or NBODY1 because they use an Ahmad–Cohen neighbor scheme (Ahmad and Cohen, 1973), which reduces the total number of full force calculations needed again (in addition to the individual hierarchical time-step scheme); that is, the proportionality factor in front of the asymptotic complexity N2 is further reduced.
We have shown that our GPU clusters for the very favorable direct N-body application reach about one-third of the theoretical peak speed sustained for a real application code with individual block time steps. In the future, we will use larger Fermi-based GPU clusters such as the Mole-8.5 cluster at the IPE/CAS in Beijing and more efficient variants of our direct N-body algorithms; details of benchmarks and science results, and the requirements to reach exascale performance, will be published elsewhere.
3.6 ADAPTIVE MESH REFINEMENT HYDROSIMULATIONS
The team at National Taiwan University has developed an adaptive mesh refinement (AMR) code named GAMER to solve astrophysical hydrodynamic problems (Schive et al., 2010). The AMR implementation is based on constructing a hierarchy of grid patches with an oct-tree data structure. The code adopts a hybrid CPU/GPU model in which both hydrodynamic and gravity solvers are implemented into the GPU and the AMR data structure is manipulated by the CPU. For strong scaling, considerable speedup is demonstrated for up to 128 GPUs, with excellent performance shown in Figures 3.6 and 3.7.
Figure 3.6 Performance speedup of the GAMER code as a function of the number of GPUs, measured on the Beijing Laohu cluster. The test problem is a purely baryonic cosmological simulation of ΛCDM, in which the root-level resolution is 2563 and seven refinement levels are used, giving 32,7683 effective resolutions. For each data point, we compare the performance by using the same number of GPUs and CPU cores. The circles and triangles show the timing results with and without the concurrent execution between CPUs and GPUs, respectively. The maximum speedup achieved in the 128-GPU run is about 24.
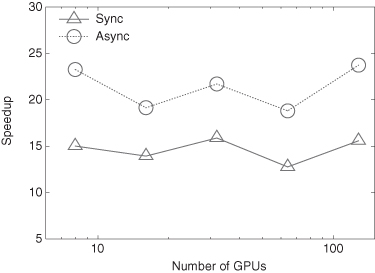
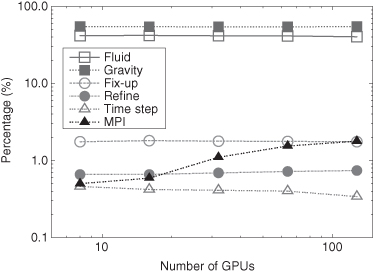
Figure 3.7 Fractions of time consumed in different parts of the GAMER code. This includes the hydrodynamic solver (open squares), gravity solver (filled squares), coarse-grid data correction (open circles), grid refinement (filled circles), computing time step (open triangles), and MPI communication (filled triangles). It shows that the MPI communication time even for large number of GPUs uses only a small percentage of time (order of 1%), and hence the code will be able to scale well to even much larger GPU numbers.
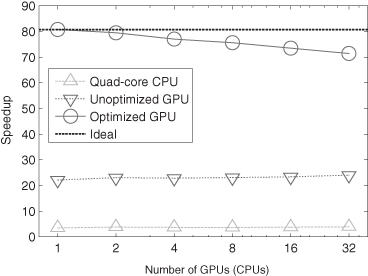
More recently, the GAMER code is further optimized for supporting several directionally unsplit hydrodynamic schemes and the OpenMP parallelization (Schive et al., accepted). By integrating hybrid MPI/OpenMP parallelization with GPU computing, the code can fully exploit the computing power in a heterogeneous CPU/GPU system. The Figure 3.8 shows the performance benchmark on the Dirac cluster at NERSC/LBNL. The maximum speedups achieved in the 32-GPU run are 71.4 and 18.3 as compared to the CPU-only 32-single-core and 32-quad-core performances, respectively. Note that the 32-GPU speedup drops about 12% mainly due to the MPI communication and the relatively lower spatial resolution (and hence higher surface/volume ratio) compared to that of the benchmark performed on the Beijing Laohu cluster. This issue can be alleviated by increasing the spatial resolution and also by overlapping communication with computation.
Figure 3.8 Performance speedup of the latest GAMER code of 2011, measured on the Dirac cluster at NERSC/LBNL. The root-level resolution is 2563 and only four refinement levels are used. The GPU performance is compared to that of CPU runs without OpenMP and GPU acceleration. Several optimizations are implemented in the fully optimized code, including the asynchronous memory copy, the concurrent execution between CPU and GPU, and the OpenMP parallelization. The quad-core CPU performance is also shown for comparison.
3.7 PHYSICAL MULTISCALE DISCRETE SIMULATION AT IPE
Discrete simulation is, in a sense, more fundamental and straightforward as compared with other numerical methods based on continuum models since the world is naturally composed of particles at very small and large scales, such as fundamental particles, atoms, and molecules on one hand and stars and galaxies on the other hand. However, continuum methods are traditionally considered more efficient as each element in these methods presents a statistically enough number of particles. This faith has changed in recent years with the dramatic development of parallel computing. It turns out that although the peak performance of (parallel) supercomputers is increasing at a speed higher than Moore’s law, the sustainable performance of most numerical softwares is far behind it, sometimes only several percent of it, and the percentage decreases with system scale inevitably. The complex data dependence and hence communication overheads inherent for most continuum-based numerical methods present a major cause of this inefficiency and poor scalability. In comparison, discrete simulation methods, such as molecular dynamic (MD) simulations, dissipative particle dynamics (DPD), lattice Boltzmann method (LBM), discrete particle methods (DEM) and SPH, and so on, heavily rely on local interactions, and their algorithms are inherently parallel. In the final analysis, this is rooted in the physical parallelism of the physical model behind these methods. It is worthy to mention that coarse-grained particles such DPD and PPM (Ge and Li, 2003a) are now capable of simulating apparently continuous systems at a computational cost fairly comparable to continuum methods, and macroscale particle methods such SPH and MaPPM (Ge and Li, 2001, 2003b) can also be understood as a special kind of numerical discretizing of continuum models.
In recent years, with the flourish of many-core computing technology, such as the use of GPUs (graphic processing unit) for scientific and engineering computing, this virtue of discrete methods is best demonstrated and further explored. A general model for many-core computing of discrete methods is “divide and conquer.” A naive implementation is to decompose the computed domain into many subdomains, which are then assigned to different processors for parallel computing of particle–particle interactions and movements. The assignment changes as the physical location of transfer from one subdomain to another. Communications, therefore, only occur at neighboring subdomains. Most practical implementations, however, use more advanced techniques, such as dynamic load balance and monotonic Lagrangian grid (Lambrakos and Boris, 1987), to minimize the waiting and communication among different processors. Within each processor, each pair of particle–particle interactions and each particle-state updating are also parallel in principle, which can be carried out by each core of the processors. Currently, most many-core processes like GPUs are still working as an external device to the CPU, so data copy between the main memory and the device memory is still necessary, and the communication between many-core processors across different computing nodes is routed by CPUs. A combined CPU–GPU computing mode is under development, which may further reduce this communication overhead.
Some of the discrete simulation work carried out at IPE/CAS using GPUs has been introduced in a Chinese monograph (Chen et al., 2009), and in some recent publications, they have covered MD simulation of multiphase micro- and nanoflow (Chen et al., 2008), polymer crystallization (Xu et al., 2009) and silicon crystal, computational fluid dynamics (CFD) simulation of cavity flow (Li et al., 2009) and gas–solid suspension, and so on. All the simulations introduced earlier have been carried out on the multiscale high-performance computing (HPC) systems established at IPE. The first system, Mole-9.7, put into use on February 18, 2008, consists of 120 HP xw8600 workstations, each installed with two NVIDIA Tesla C870 GPGPU cards and two Intel Xeon 5430 CPUs, and reached a peak performance of 120 teraflops in a single precision. The system is connected by an all-to-all switch together with a 2-D torus topology of Gigabit Ethernet, which speeds up adjacent communication dominated in discrete simulations. Its successor, Mole-8.7, is announced on April 20, 2009 as the first supercomputer of China with 1.0-petaflop peak performance in a single precision (Chen et al., 2009). Both NVIDIA and AMD GPU are integrated in this system. The designing philosophy is the consistency among hardware, software, and the problems to be solved, based on the multiscale method and discrete simulation approaches developed at IPE. The system has nearly 400 nodes connected by Gigabit Ethernet and DDR InfiniBand network.
Then, in 2010, IPE built the new system, Mole-8.5, which is the first GPU cluster using Fermi in the world. With the powerful computational resource of Mole-8.5 and the multiscale software developed by IPE, several large-scale applications have been successfully run on Mole-8.5:
- An MD simulation of dynamic structure of a whole H1N1 influenza virion in solution is simulated at the atomic level for the first time. The simulation system includes totally 300 million atoms in a periodic cube with an edge length of 148.5 nm. Using 288 nodes with 1728 Fermi Tesla C2050, the simulation proceeds at 770 ps/day with an integration time step of 1fs (Xu et al., 2010b).
- A quasi-real-time DEM simulation of an industrial rotating drum, the size of which is 13.5 m long by 1.5 m in diameter, is performed. The simulation system contains about 9.6 million particles. Nearly 1/11 real speed is achieved using 270 GPUs together with online visualization (Xu et al., 2010a).
- Large-scale direct numerical simulations of gas–solid fluidization have been carried out, with systems of about 1 million solid particles and 1 billion fluid particles in 2-D using 576 GPUs, and of about 100,000 solid particle and 0.4 billion fluid particles in 3-D using 224 GPUs. The largest system we have run utilized 1728 GPUs with an estimated performance of 33 teraflops in double precision (Xiong et al., 2010).
- A large-scale parallel MD simulation of single-crystalline silicon nanowire containing about 1.5 billion silicon atoms with many-body potential is conducted using 1500-GPU cards with a performance of about 227 teraflops in single precision (Hou and Ge, 2011).
3.8 DISCUSSION AND CONCLUSIONS
We have presented exemplary implementations of parallel codes using many GPUs as accelerators, so combining message passing parallelization with many-core parallelization, and have discussed their benchmarks using up to 512 Fermi Tesla GPUs in parallel, mostly on the Mole-8.5 hardware of the IPE/CAS in Beijing, but also on the Laohu Tesla C1070 cluster of the National Astronomical Observatories of CAS in Beijing and smaller clusters in Germany and in the United States. For direct high-accuracy gravitating N-body simulations, we discussed how self-gravity, because it cannot be shielded, generates inevitably strong multiscale structures in space and time, spanning many orders of magnitude. This requires special codes, which nevertheless scale with a high efficiency on GPU clusters. Also, we present an adaptive mesh hydrodynamic code including a gravity solver using FFT and relaxation methods and physical algorithms used for multiscale flows with particles. So, our codes are examples that it is possible to reach the subpetaflop scale in sustained speed for realistic application software with large GPU clusters. Whether our programming models can be scaled up for future hardware and the exaflop scale, however, remains yet to be studied.
ACKNOWLEDGMENTS
CAS has supported this work by a Visiting Professorship for Senior International Scientists, Grant Number 2009S1-5 (RS), and NAOC/CAS through the Silk Road Project (RS, PB, JF partly). IPE/CAS and the High Performance Computing Center at NAOC/CAS acknowledge financial support by the Ministry of Finance under the grant ZDYZ2008-2 for the supercomputers Mole-8.5 and Laohu, used for simulations of this chapter. RS and PB want to thank Xue Suijian for valuable advice and support. We thank the computer system support team at NAOC (Gao Wei and Cui Chenzhou) for their support to run the Laohu cluster.
We gratefully acknowledge computing time on the Dirac cluster of NERSC/LBNL in Berkeley and thank Hemant Shukla, John Shalf, and Horst Simon for providing the access to this cluster and for cooperation in the International Center of Computational Science,7 as well as the helpful cooperation of Guillermo Marcus, Andreas Kugel, Reinhard Männer, Robi Banerjee, and Ralf Klessen in the GRACE and Frontier Projects at the University of Heidelberg (at ZITI and ITA/ZAH).
Simulations were also performed on the GRACE supercomputer (grants I/80 041-043 and I/81 396 of the Volkswagen Foundation and 823.219-439/30 and /36 of the Ministry of Science, Research and the Arts of Baden-Württemberg) and the Kolob cluster funded by the Frontier Project at the University of Heidelberg. PB acknowledges the special support by the NAS Ukraine under the Main Astronomical Observatory GRAPE/GRID computing cluster project.8 PB’s studies are also partially supported by the program Cosmomicrophysics of NAS Ukraine. The Kolob cluster and IB have been funded by the excellence funds of the University of Heidelberg in the Frontier scheme. Though our parallel GPU code has not yet reached the perfection of standard NBODY6, we want to thank Sverre Aarseth for providing his codes freely and for teaching many generations of students how to use it and adapt it to new problems. This has helped and guided the authors in many respects.
Notes
6 http://www.ast.cam.ac.uk/∼sverre/web/pages/nbody.htm.
8 http://www.mao.kiev.ua/golowood/eng/.
REFERENCES
S. J. Aarseth. Star cluster simulations: The state of the art. Celestial Mechanics and Dynamical Astronomy, 73:127–137, 1999a.
S. J. Aarseth. From NBODY1 to NBODY6: The growth of an industry. Publications of the Astronomical Society of the Pacific, 111:1333–1346, 1999b.
S. J. Aarseth. Gravitational N-Body Simulations. Cambridge, UK: Cambridge University Press, 2003.
A. Ahmad and L. Cohen. A numerical integration scheme for the N-body gravitational problem. Journal of Computational Physics, 12:389–402, 1973.
K. Akeley, H. Nguyen, and NVIDIA. GPU Gems 3. Addison-Wesley Professional, 2007.
J. Barnes and P. Hut. A hierarchical O(N log N) force-calculation algorithm. Nature, 324:446–449, 1986.
B. R. Barsdell, D. G. Barnes, and C. J. Fluke. Advanced architectures for astrophysical supercomputing. ArXiv e-prints, 2010.
R. G. Belleman, J. Bédorf, and S. F. Portegies Zwart. High performance direct gravitational N-body simulations on graphics processing units II: An implementation in CUDA. New Astronomy, 13:103–112, 2008.
P. Berczik, D. Merritt, and R. Spurzem. Long-term evolution of massive black hole binaries. II. Binary evolution in low-density galaxies. The Astrophysical Journal, 633:680–687, 2005.
P. Berczik, D. Merritt, R. Spurzem, et al. Efficient merger of binary supermassive black holes in nonaxisymmetric galaxies. The Astrophysical Journal Letters, 642:L21–L24, 2006.
P. Berczik, N. Nakasato, I. Berentzen, et al. Special, hardware accelerated, parallel SPH code for galaxy evolution. In SPHERIC—Smoothed particle hydrodynamics european research interest community, 2007.
P. Berczik, K. Nitadori, T. Hamada, et al. The parallel GPU N-body code φGPU. in preparation, 2011.
I. Berentzen, M. Preto, P. Berczik, et al. Binary black hole merger in galactic nuclei: Post-Newtonian simulations. The Astrophysical Journal, 695:455–468, 2009.
F. Chen, W. Ge, and J. Li. Molecular dynamics simulation of complex multiphase flows—Test on a GPU-based cluster with customized networking. Science in China. Series B, 38:1120–1128, 2008.
F. Chen, W. Ge, L. Guo, et al. Multi-scale HPC system for multi-scale discrete simulation. Development and application of a supercomputer with 1Petaflop/s peak performance in single precision. Particuology, 7:332–335, 2009.
H. M. P. Couchman, P. A. Thomas, and F. R. Pearce. Hydra: An adaptive-mesh implementation of P 3M-SPH. The Astrophysical Journal, 452:797, 1995.
Y. Cui, Y. Chen, and H. Mei. Improving performance of matrix multiplication and FFT on GPU. In 15th International Conference on Parallel and Distributed Systems, 729:13, 2009.
W. Dehnen. A very fast and momentum-conserving tree code. The Astrophysical Journal Letters, 536:L39–L42, 2000.
W. Dehnen. A hierarchical O(N) force calculation algorithm. Journal of Computational Physics, 179:27–42, 2002.
E. N. Dorband, M. Hemsendorf, and D. Merritt. Systolic and hyper-systolic algorithms for the gravitational N-body problem, with an application to Brownian motion. Journal of Computational Physics, 185:484–511, 2003.
M. Fellhauer, P. Kroupa, H. Baumgardt, et al. SUPERBOX—An efficient code for collisionless galactic dynamics. New Astronomy, 5:305–326, 2000.
T. Fukushige, J. Makino, and A. Kawai. GRAPE-6A: A single-card GRAPE-6 for parallel PC-GRAPE cluster systems. Publications of the Astronomical Society of Japan, 57, 2005.
W. Ge and J. Li. Macao-scale pseudo-particle modeling for particle-fluid systems. Chinese Science Bulletin, 46:1503–1507, 2001.
W. Ge and J. Li. Macro-scale phenomena reproduced in microscopic systems-pseudo-particle modeling of fludization. Chemical Engineering Science, 58:1565–1585, 2003a.
W. Ge and J. Li. Simulation of particle-fluid systems with macro-scale pseudo-particle modeling. Powder Technology, 137:99–108, 2003b.
L. Greengard and V. Rokhlin. A fast algorithm for particle simulations. Journal of Computational Physics, 73:325–348, 1987.
A. Gualandris and D. Merritt. Ejection of supermassive black holes from galaxy cores. The Astrophysical Journal, 678:780–797, 2008.
T. Hamada and T. Iitaka. The Chamomile scheme: An optimized algorithm for N-body simulations on programmable graphics processing units. ArXiv Astrophysics e-prints, 2007.
S. Harfst, A. Gualandris, D. Merritt, et al. Performance analysis of direct N-body algorithms on special-purpose supercomputers. New Astronomy, 12:357–377, 2007.
R. W. Hockney and J. W. Eastwood. Computer Simulation Using Particles. Bristol, UK: Hilger, 1988.
C. Hou and W. Ge. GPU-accelerated molecular dynamics simulation of solid covalent crystals. Molecular Simulation, submitted, 2011.
W.-M.-W. Hwu. GPU Computing Gems. Morgan Kaufman Publ. Inc., 2011.
T. Ishiyama, T. Fukushige, and J. Makino. GreeM: Massively parallel TreePM code for large cosmological N-body simulations. Publications of the Astronomical Society of Japan, 61:1319, 2009.
A. Just, F. M. Khan, P. Berczik, et al. Dynamical friction of massive objects in galactic centres. The Monthly Notices of the Royal Astronomical Society, 411:653–674, 2011.
S. Komossa, V. Burwitz, G. Hasinger, et al. Discovery of a binary active galactic nucleus in the ultraluminous infrared galaxy NGC 6240 using Chandra. The Astrophysical Journal Letters, 582:L15–L19, 2003.
S. G. Lambrakos and J. P. Boris. Geometric properties of the monotonic lagrangian grid algorithm for near neighbor calculations. Journal of Computational Physics, 73:183, 1987.
K. J. Lee, N. Wex, M. Kramer, et al. Gravitational wave astronomy of single sources with a pulsar timing array. ArXiv e-prints, 2011.
B. Li, X. Li, Y. Zhang, et al. Lattice Boltzmann simulation on NVIDIA and AMD GPUs. Chinese Science Bulletin, 54:3178–3185, 2009.
D. Lynden-Bell and R. Wood. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. The Monthly Notices of the Royal Astronomical Society, 138:495, 1968.
J. Makino. A modified Aarseth code for GRAPE and vector processors. Proceedings of Astronomical Society of Japan, 43:859–876, 1991.
J. Makino. A fast parallel treecode with GRAPE. Publications of the Astronomical Society of Japan, 56:521–531, 2004.
J. Makino and P. Hut. Performance analysis of direct N-body calculations. The Astrophysical Journal Supplement Series, 68:833–856, 1988.
J. Makino and S. J. Aarseth. On a Hermite integrator with Ahmad-Cohen scheme for gravitational many-body problems. Publications of the Astronomical Society of Japan, 44:141–151, 1992.
J. Makino, T. Fukushige, M. Koga, et al. GRAPE-6: Massively-parallel special-purpose computer for astrophysical particle simulations. Publications of the Astronomical Society of Japan, 55:1163–1187, 2003.
K. Nitadori and J. Makino. Sixth- and eighth-order Hermite integrator for N-body simulations. New Astronomy, 13:498–507, 2008.
S. Pasetto, E. K. Grebel, P. Berczik, et al. Orbital evolution of the Carina dwarf galaxy and self-consistent determination of star formation history. Astronomy & Astrophysics, 525:A99, 2011.
F. R. Pearce and H. M. P. Couchman. Hydra: A parallel adaptive grid code. New Astronomy, 2:411–427, 1997.
S. F. Portegies Zwart, R. G. Belleman, and P. M. Geldof. High-performance direct gravitational N-body simulations on graphics processing units. New Astronomy, 12:641–650, 2007.
M. Preto, I. Berentzen, P. Berczik, et al. Fast coalescence of massive black hole binaries from mergers of galactic nuclei: Implications for low-frequency gravitational-wave astrophysics. ArXiv e-prints, 2011.
H.-Y. Schive, Y.-C. Tsai, and T. Chiueh. GAMER: A graphic processing unit accelerated adaptive-mesh-refinement code for astrophysics. Astrophysical Journal Supplement Series, 186:457–484, 2010.
H.-Y. Schive, U.-H. Zhang, and T. Chiueh. Directionally unsplit hydrodynamic schemes with hybrid MPI/OpenMP/GPU parallelization in AMR. The International Journal of High Performance Computing Applications, accepted for publication.
V. Springel. The cosmological simulation code GADGET-2. Monthly Notices of the Royal Astronomical Society, 364:1105–1134, 2005.
R. Spurzem. Direct N-body simulations. Journal of Computational and Applied Mathematics, 109:407–432, 1999.
R. Spurzem, P. Berczik, G. Hensler, et al. Physical processes in star-gas systems. Publications of the Astronomical Society of Australia, 21:188–191, 2004.
R. Spurzem, P. Berczik, I. Berentzen, et al. From Newton to Einstein—N-body dynamics in galactic nuclei and SPH using new special hardware and astrogrid-D. Journal of Physics Conference Series, 780(1):012071, 2007.
R. Spurzem, I. Berentzen, P. Berczik, et al. Parallelization, special hardware and post-Newtonian dynamics in direct N-body simulations. In S. J. Aarseth, C. A. Tout, and R. A. Mardling, editors, The Cambridge N-Body Lectures, volume 760 of Lecture Notes in Physics, Berlin: Springer Verlag, 2008.
R. Spurzem, P. Berczik, G. Marcus, et al. Accelerating astrophysical particle simulations with programmable hardware (FPGA and GPU). Computer Science—Research and Development (CSRD), 23:231–239, 2009.
R. Spurzem, P. Berczik, K. Nitadori, et al. Astrophysical particle simulations with custom GPU clusters. In 10th IEEE International Conference on Computer and Information Technology, pp. 1189, 2010.
R. Spurzem, P. Berczik, T. Hamada, et al. Astrophysical particle simulations with large custom GPU clusters on three continents. In International Supercomputing Conference ISC 2011, Computer Science—Research and Development (CSRD), accepted for publication, 2011.
A. C. Thompson, C. J. Fluke, D. G. Barnes, et al. Teraflop per second gravitational lensing ray-shooting using graphics processing units. New Astronomy, 15:16–23, 2010.
P. Wang and T. Abel. Magnetohydrodynamic simulations of disk galaxy formation: The magnetization of the cold and warm medium. The Astrophysical Journal, 696:96–109, 2009.
P. Wang, T. Abel, and R. Kaehler. Adaptive mesh fluid simulations on GPU. New Astronomy, 15:581–589, 2010a.
X. Wang, W. Ge, X. He, et al. Development and application of a HPC system for multi-scale discrete simulation—Mole-8.5. In International Supercomputing Conference ISC10, 2010b.
H.-C. Wong, U.-H. Wong, X. Feng, et al. Efficient magnetohydrodynamic simulations on graphics processing units with CUDA. ArXiv e-prints, 2009.
Q. Xiong, et al. Large-scale DNS of gas-solid flow on Mole-8.5. Chemical Engineering Science, submitted, 2010.
G. Xu. A new parallel n-body gravity solver: TPM. Astrophysical Journal Supplement Series, 98:355, 1995.
J. Xu, Y. Ren, X. Yu, et al. Molecular dynamics simulation of macromolecules using graphics processing unit. Molecular Simulation, submitted, 2009.
J. Xu, H. Qi, X. Fang, et al. Quasi-realtime simulation of rotating drum using discrete element method with parallel GPU computing. Particulogy, in press, 2010a.
J. Xu, X. Wang, X. He, et al. Application of the Mole-8.5 supercomputer—Probing the whole influenza virion at the atomic level. Chinese Science Bulletin, in press, 2010b.
R. Yokota and L. Barba. Treecode and fast multipole method for N-body simulation with CUDA. ArXiv e-prints, 2010.
R. Yokota, J. P. Bardhan, M. G. Knepley, et al. Biomolecular electrostatics using a fast multipole BEM on up to 512 GPUs and a billion unknowns. ArXiv e-prints, 2010.
K. Yoshikawa and T. Fukushige. PPPM and TreePM methods on GRAPE systems for cosmological N-body simulations. Publications of the Astronomical Society of Japan, 57:849–860, 2005.
